CAPITOLO 3
LA VISIBILITA’ PIASTRA-PIASTRA
3.1 Lo spazio duale
Il computo della visibilità piastra-piastra è una problematica affrontata da più di 10 anni in CG, con una varietà di soluzioni proposte. Queste tecniche solitamente costruiscono nello spazio duale una struttura in grado di fornire le informazioni necessarie sui cosiddetti eventi di visibilità, ovvero eventi che occorrono quando si verifica una variazione nella visibilità topologica di uno scenario (ad esempio, quando il punto di vista si sposta in modo che uno spigolo precedentemente invisibile perché occluso da un ostacolo diviene visibile). Tali strutture, e tali tecniche, sono utili anche per risolvere il più semplice problema di stimare se una piastra risulta essere visibile o invisibile da un’altra. La struttura che andremo ad usare è analoga al cosiddetto “complesso di visibilità” introdotto da Pocchiola e Vegter [14], ovvero un complesso a celle bidimensionale1 immerso in 3D.
L’algoritmo che si è scelto di implementare è una versione modificata del Line Space Partitioning introdotto da Bittner e Přikryl (si vedano [16], [17]). Tale tecnica effettua un mappaggio di linee orientate dello spazio bidimensionale (spazio primario) in punti ancora in 2D dello spazio proiettivo orientato (SPO), o spazio duale. Lo SPO presenta notevoli vantaggi rispetto al classico spazio proiettivo (si vedano [18], [19]); in esso è possibile definire una orientazione per i piani e le linee, e di conseguenza viene eliminata l’ambiguità sulle direzioni e sui segmenti2 in modo da rendere possibile
definire delle figure convesse come nello spazio reale. Esso inoltre mantiene la dualità della geometria proiettiva classica. Si consideri infatti il mappaggio (contrassegnato da ‘ * ‘) di un punto nello spazio proiettivo, e viceversa, che trasforma il punto di coordinate (x, y, z) nella linea il cui vettore direttore è <x, y, z>. Il mappaggio preserva l’incidenza: se il punto p è sulla retta l nello spazio primario, la linea p* passerà attraverso il punto l*. Generalizzando, si può dire che ogni definizione o algoritmo
1
Si veda l’Appendice.
2
Nella geometria proiettiva gli estremi di un segmento vengono mappati attraverso una proiezione centrale in due punti sulla sfera di raggio unitario, dividendo la circonferenza che passa per essi in due archi semplici; non c’è modo di distinguere l’uno dall’altro.
della geometria proiettiva ha un duale, ottenuto scambiando le parole “punto” e “linea”.
Nello spazio duale (come vedremo, chiamato anche line space) è possibile manipolare insiemi di raggi molto più semplicemente rispetto allo spazio primario [15]. Per il mappaggio vengono usate le cosiddette coordinate di Plücker in 2D, che saranno descritte nei paragrafi successivi.
3.1.1 Coordinate di Plücker di una retta
Le coordinate di Plücker possono essere usate per rappresentare all’interno di uno spazio di dimensione d un piano di rango k, con 1< <k d (k=2 per le linee). Esse descrivono analiticamente un piano come una j-tupla dove j d 1
k +
⎛ ⎞
= ⎜ ⎟
⎝ ⎠. Questa j-tupla può essere interpretata come le coordinate omogenee di un punto in uno SPO di dimensione j –1 [19].
Assumiamo che l sia una retta orientata in 2
R e che u=( ,u ux y) e v=( ,v vx y) siano due punti distinti che giacciono su l. La retta l orientata da u verso v è descritta dalla seguente matrice:
1
1
x y l x yu u
M
v v
⎛
⎞
= ⎜
⎜
⎟
⎟
⎝
⎠
(6)dove l’ultima colonna indica il verso della retta (se l’orientazione fosse stata da v ad u, avremmo avuto l’opposto del vettore unitario). Le coordinate di Plücker l* di l sono i minori di Ml :
* * * *
(
x,
y,
z)
(
y y,
x x,
x y x y)
l
=
l
l
l
=
u
−
v
v
−
u
u v
−
v u
(7) La j-tupla l* può essere interpretata come coordinate omogenee di un punto nello spazio proiettivo orientato 2D. l* non è affetta dalla scelta dei punti u e v che sono usati per descrivere l, eccetto che per un fattore di scala positivo. Più precisamente,due rette orientate sono uguali se e solo se le loro coordinate di Plücker differiscono soltanto di un fattore di scala positivo.
Le coordinate di l* corrispondono anche ai coefficienti dell’equazione implicita della retta. Consideriamo infatti una retta l’ di equazione ' :l ax by+ + = . Essa viene c 0 mappata nei punti *
1
l = (a, b, c) e l2* = - (a, b, c), dove l1* e l2*sono i punti che giacciono su piani coincidenti ma con orientazione opposta (si pensi per semplicità ad un foglio a due facce) indotta da l’ ; in altre parole, *
1
l e l2* sono i due punti indotti dalla medesima retta l’ quando assume le sue due possibili orientazioni. Le coordinate omogenee spesso vengono normalizzate, in modo da ottenere ad esempio *
( / , 1, / ) N
l = a b c b . Tuttavia la normalizzazione introduce una singolarità: nel nostro esempio, le linee parallele all’asse y vengono mappate in punti all’infinito. Per evitare queste singolarità, conviene trattare lo SPO 2D come uno spazio tridimensionale lineare (ovvero uno spazio dove tutti i piani intercettano l’origine) chiamato line space L. Di conseguenza, l* è una semiretta uscente dall’origine in L; tutti i punti sulla semiretta l* rappresentano la stessa retta orientata l.
3.1.2 Rette passanti per un punto
Fasci di rette passanti attraverso un punto 2 ( x, y)
p= p p ∈R vengono mappati in un piano p* orientato in L che è espresso da:
{
}
*
( , , ) : x y 0
p = x y z ∈L p x+p y+ =z (8)
Questo piano suddivide L in due semispazi aperti *
p+ e p−*. I punti in p*− corrispondono a rette orientate che passano in senso orario attorno a p secondo la regola della mano destra; i punti in *
p+ parimenti corrispondono a rette orientate che passano in senso antiorario attorno a p (naturalmente queste relazioni dipendono dall’orientazione nello spazio primario); si veda a proposito la fig. 3.1. Possiamo inoltre chiamare – p* un piano orientato opposto a p* che può essere epresso da
{
}
*
( , , ) : x y 0
p x y z L p x p y z
3.1.3 Rette passanti attraverso un segmento
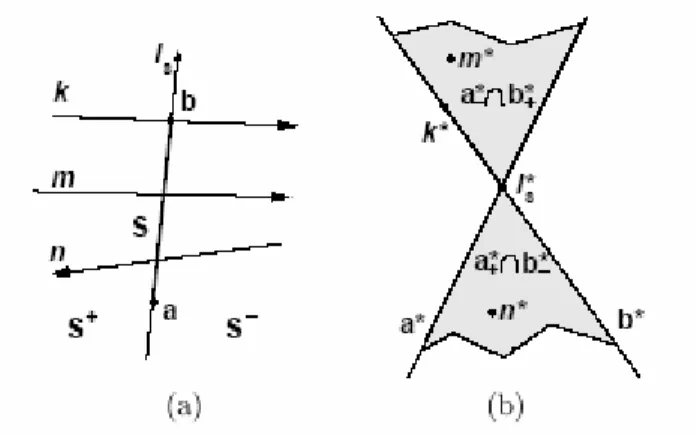
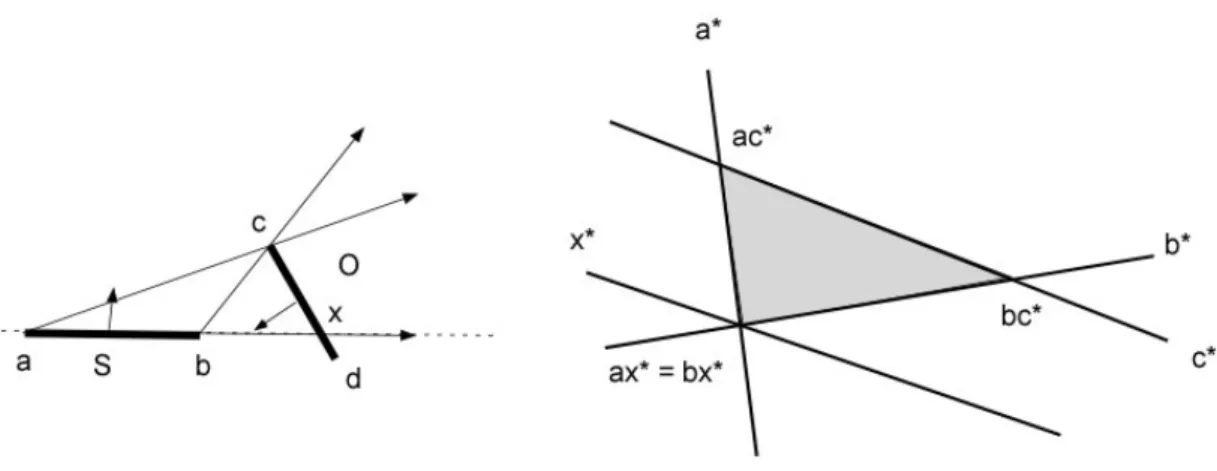
Le rette orientate passanti attravero un segmento possono essere decomposte in due insiemi caratterizzati dal “lato” dal quale le rette provengono. Consideriamo infatti una retta di supporto lS di un segmento S, che partiziona il piano in due semipiani aperti
S+e S−. Chiamiamo inoltre a e b i due estremi del segmento e a* e b* i loro duali nello SPO. Le rette orientate che intercettano S provenendo da S− possono essere espresse in L come l’intersezione dei semispazi *
a+ e b−*. Similmente le rette che intercettano S provenendo da S+ sono espresse come * *
a−∩ . Si veda a proposito la fig. 3.2. b+
Figura 3.1 - (a) quattro rette passanti per un punto p nello spazio reale; (b) proiezione nello spazio duale del punto p e delle rette passati attraverso di esso; (c) vista della situazione nello spazio duale attraverso la proiezione su un piano perpendicolare a p*
Figura 3.2 – (a) segmento S e tre rette che lo intercettano; (b) situazione nello spazio duale: la proiezione delle linea di supporto lS di S sono due
piani che si intersecano nella semiretta lS*. La linea k intercetta il punto a
e quindi viene mappata sul piano a*. Le linee m e n vengono proiettate nelle due semirette corrispondenti alla loro orientazione.
3.1.4 Rette passanti attraverso due segmenti
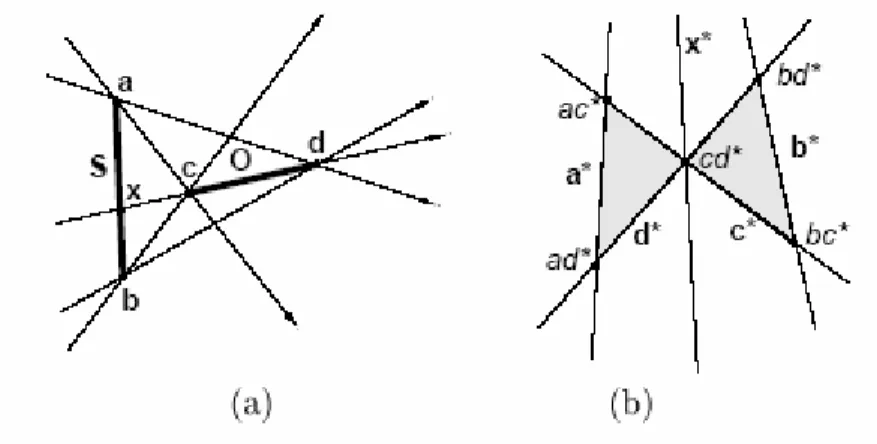
L’insieme delle rette passanti attraverso due segmenti di retta possono essere descritti come l’intersezione di quattro semispazi in L. I quattro semispazi corrispondono al mappaggio degli estremi dei due segmenti. Poiché i piani passano attraverso l’origine di L, l’intersezione dei semispazi da essi indotti è una piramide non chiusa con l’apice nell’origine. Gli spigoli della piramide corrispondono al mappaggio delle quattro rette critiche indotte dai due segmenti; con riferimento alla fig 3.3, classificheremo queste rette come “rette di separazione” (le rette ad e bc) e “rette di supporto” (le rette ac e bd): le prime delimitano la regione dietro cd dove ab è parzialmente visibile, le seconde la regione dietro cd dove ab non è visibile. Chiamiamo quindi P(S, O) questa piramide nello spazio duale corrispondente alle rette che intercettano i segmenti S e O: essa può essere rappresentata dal corrispondente albero BSP, che chiameremo poliedro di blocco B(S, O) (fig. 3.4). Poiché P(S, O) non è chiusa, i vertici di B(S, O) possono giacere in qualsiasi punto sulle semirette coincidenti con gli spigoli della piramide. Per convenienza useremo allora vertici che sono l’intersezione degli spigoli di P(S, O) con la sfera unitaria il cui centro è l’origine di L.
Figura 3.3 – (a) due segmenti e le corrispondenti quattro rette critiche che vanno da ab a cd. Le rette di separazione ad e cd limitano la regione di visibilità parziale tra ab e cd. Le rette di supporto ac e bd delimitano la regione d’ombra indotta da cd rispetto a ab. (b) la piramide P(S, O), rappresentata per semplicità in 2D (vista dall’alto).
In fig. 3.5, le linee di supporto di cd intercettano ab nel punto x. L’insieme di linee passanti attraverso ab e cd può allora essere decomposto in rette passanti attraverso ax e cd, e attraverso xb e cd. Le rette orientate attraverso ax e cd vengono mappate in una piramide che è descritta dall’intersezione di tre soli semispazi indotti dal mappaggio di
a, x e b. Le linee orientate attraverso xb e cd possono essere descritte similmente. La scelta di quale tra le due piramidi selezionare dipenderà in primo luogo da quale tra le due è la piastra sorgente e in seconda istanza dalla normale ai segmenti, ovvero dall’orientazione dei segmenti nello spazio primario.
Figura 3.4 – Poligono di blocco B(S,0) corrispondente alla piramide di fig. 3.3
Figura 3.5 – (a) Configurazione degenere dei segmenti: la linea di supporto cd intercetta ab nel punto x. Ci sono 5 rette critiche. (b) Nello spazio duale si hanno due piramidi che condividono uno spigolo corrispondente alla linea cd
3.1.5 Rette passanti per un insieme di segmenti
Consideriamo un insieme di n + 1 segmenti. Chiameremo uno di questi segmenti la “sorgente” (S) e i restanti n “occlusori”, che classificheremo con la notazione Ok, 1≤ ≤ . Vogliamo stabilire la visibilità tra gli occlusori e la sorgente. Lo studio della k n visibilità di un occlusore Ok può essere effettuato attraverso le rette che corrispondono
alle piramidi ( ,P S Ok). Sappiamo infatti che ( ,P S Ok) descrive l’insieme delle rette che giacciono nelle zone d’ombra e di visibilità parziale indotte da Ok. Sappiamo anche che le rette che connettono Ok e S possono essere bloccate da altri occlusori Ox o da una combinazione di occlusori Ox, 1≤ ≤ , che giacciono tra S e x n Ok. Dovremo allora confrontare in qualche modo le piramidi ( ,P S Ok) e ( ,P S Ox): se la prima giace completamente “dentro” la seconda, possiamo essere sicuri che Ok è invisibile da
S. Per la teoria degli insiemi, questa operazione equivale alla sottrazione di ( ,P S Ok) da ( , x)
P S O . Generalizzando per un insieme di Ox, possiamo allora scrivere:
1
( ,
k)
( ,
k)
( ,
x)
x nV S O
P S O
P S O
≤ ≤=
−
U
(9) ( , k)V S O è il sottoinsieme della piramide ( ,P S Ok) che rappresenta le rette orientate attraverso le quali Ok è visibile da S. A sua volta, tutte le rette orientate corrispondenti a V S O( , k) sono bloccate da Ok. Se V S O( , k) è l’insieme vuoto l’occlusore Ok è invisibile.
Quanto detto suggerisce di costruire incrementalmente un “oggetto” formato dall’unione delle piramidi ( ,P S Ok). Assumiamo infatti che si possano processare tutti gli occlusori in ordine front-to-back rispetto alla sorgente data; supponiamo inoltre di aver già processato k occlusori e di essere in grado di aggiornare l’unione Ak delle piramidi ( ,P S Ok) che corrisponde alle rette bloccate da questi k occlusori. Con riferimento alla (8), possiamo allora determinare V S O( , k+1) e Ak+1:
1 1 1 1 1
( ,
)
( ,
)
( ,
)
( ,
)
k k k k k k k kV S O
P S O
A
A
A
P S O
A
V S O
+ + + + +=
−
=
∪
=
∪
(10)Per meglio comprendere come lavori l’algoritmo, si prenda l’esempio seguente con riferimento alla fig. 3.6
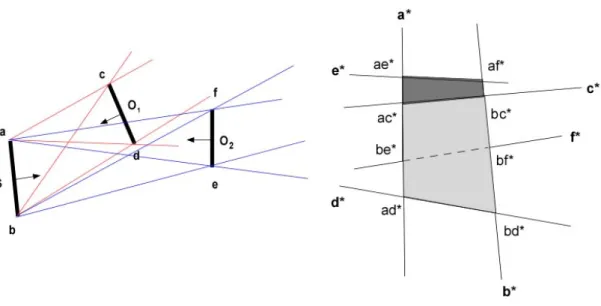
Figura 3.6 – Costruzione di Ak+1
La prima piastra ad essere elaborata è la O1; la relativa piramide P S O( , 1)è quella che
ha per spigoli ac*, ad*, bc* e bd* e naturalmente essa corriponderà a V S O( , 1) e ad A1.
Successivamente, alla piastra O2 verrà associata la piramide P S O( , 2) di spigoli ae*,
af*, be* e bf*. Come si può vedere in figura, P S O( , 2)è in parte compresa e in parte
esterna ad A1; in particolare, V S O( , 2)corrisponde alla regione di spazio marcata in
grigio scuro. L’ “oggetto” A2sarà allora pari all’unione tra A1 e V S O( , 2).
Naturalmente il procedimento può essere ripetuto per tutte le piastre.
Ricordando che le piramidi ( ,P S Ok) sono rappresentate dai relativi poliedri di blocco ( , k)
B S O , si può affermare che ci siamo in qualche modo riportati al caso della visibilità punto-piastra e all’algoritmo SVBSP descritti nel Capitolo 2. Per lo studio della visibilità piastra-piastra necessiteremo infatti di un ordinamento front-to-back per le piastre da processare, di alberi binari BSP che descrivano una particolare regione di spazio (in questo caso quelle di ombra e di visibilità parziale indotte da un occlusore
1 k
O + rispetto alla sorgente, ovvero la piramide P S O( , k+1)), di un albero che rappresenti tale regione da aggiornare passo dopo passo (l’ “oggetto” Ak) e infine dell’operazione di aggiornamento che corriponde al “filtraggio” tra questi alberi (per determinare sia la visibilità , ovvero V S O( , k+1), sia il nuovo albero, l’oggetto Ak+1).
3.2 Descrizione generale dell’algoritmo Line Space Partitioning (LSP) semplificato
L’algoritmo LSP semplificato si basa su tre passi consecutivi. Date le n piastre che rispondono all’ipotesi di lavoro e sceltane una come sorgente S, per ogni piastra k tra le n – 1 rimanenti (gli occlusori) sono necessari i seguenti passaggi:
• la costruzione del poliedro di blocco ( ,B S Ok): la piramide ( ,P S Ok) relativa alle zone d’ombra e di visibilità parziale indotte da Ok viene rappresentata attraverso il relativo albero BSP;
• la determinazione della visibilità della piastra k: ( ,B S Ok) viene filtrato attraverso l’albero Regional Occlusion Tree (ROT), ovvero attraverso la rappresentazione tramite albero BSP dell’oggetto Ak−1; questa operazione,
similmente a quanto visto per l’algoritmo SVBSP, permette di verificare la visibilità della piastra k rispetto alla sorgente S ;
• l’aggiornamento del ROT: il ROT viene aggiornato per tener conto di
( , k)
V S O , ottenendo l’oggetto Ak.
Il metodo deve naturalmente essere iterato in modo che ogni piastra sia considerata sorgente: ciò significa usare due cicli annidati ognuno di n loop.
A questo punto è importante premettere che ogni nodo sia di ( ,B S Ok) che del ROT è formato da:
un partizionatore: il piano p* passante per l’origine in L, ovvero la trasformata di uno dei vertici, diciamo quello p, dei due top edge nello spazio primario coinvolti nella costruzione di ( ,B S Ok);
due sub-partizionatori: le semirette l1* e l2* uscenti dall’origine di L, corrispondenti alle trasformate delle due rette l1 e l2 (una di supporto, l’altra di separazione) passanti per il vertice p nello spazio primario; tali semirette sono gli spigoli della piramide ( ,P S O k) che giacciono sul piano p*, ovvero l’intersezione di p* con altri due piani di supporto delle facce della piramide ( ,P S O . k)
Dato le particolarità del line space a cui si è accennato, per l’implementazione del nodo saranno sufficienti 3 campi REAL per la memorizzazione dei coefficienti dell’equazione del piano p* e ulteriori 9 campi REAL per registrare le coordinate 3D dei due vertici della piramide che giacciono su l1* e l2* , oltre naturalmente a due puntatori per il sottoalbero negativo e positivo e un ulteriore puntatore alla lista degli ostacoli.
Si deve ricordare inoltre che l’algoritmo lavora in 2.5D: anche in questo caso quindi la determinazione della visibilità della piastra k rispetto alla sorgente viene effetuata attraverso un insieme di condizioni che agiscono prima sulle informazioni 2D (attraverso le quali si opera la trasformazione nel line space) e successivamente sulla terza dimensione. Tali condizioni sono in tutto analoghe a quelle già viste per la fase di predizione (cfr. Cap. 2, § 2.2, “Condizioni di visibilità e invisibilità”); se ne riporta il sunto in tabella 6.
INVISIBILITA’ VISIBILITA’
ANALISI 2D Condizione necessaria non sufficiente Condizione sufficiente non necessaria OPERATORE
LOGICO AND OR
ANALISI ALTEZZE complementare Condizione supplementare Condizione Tabella 6 – condizioni di visibilià e invisibilità dell’algoritmo LSP
Assumendo che in questo caso il punto di vista coincida con il centro del top edge della piastra sorgente, le condizioni sopra riportate assumono i seguenti significati:
condizione necessaria non sufficiente: tutti i frammenti del poliedro di blocco ( , k)
condizione complementare: in tutte le celle interne il raggio che connette il punto di vista allo spigolo superiore della piastra k deve essere intercettato dagli ostacoli presenti nella cella;
condizione sufficiente non necessaria: almeno un frammento del poliedro di blocco ( , k)
B S O deve raggiungere una foglia esterna del ROT;
condizione supplementare: per almeno una cella interna dove è giunto un frammento del poliedro di blocco ( ,B S Ok) si deve verificare che nessuno degli ostacoli intercetti il raggio che connette il punto di vista allo spigolo superiore della piastra k.
Nelle condizioni precedenti si è accennato a “frammenti” di ( ,B S Ok); ciò è corretto se si pensa all’operazione di filtraggio di due alberi BSP [11]. Assumiamo infatti che gli alberi T1 e T2 descrivano due diverse partizioni dello stesso spazio R.
Per ogni nodo dell’albero “filtrante” T1, ogni partizionatore associato ai nodi
dell’albero “filtrato” T2 viene confrontato con il partizionatore registrato nel nodo
corrente dell’albero T1. Se i piani associati ai nodi dei due alberi sono orientati
correttamente, nel nostro caso tale operazione da origine per ogni coppia p1 (partizionatore associato al nodo corrente di T1) - p2 (partizionatore associato al nodo corrente di T2) a quattro possibili eventi: il partizionatore p2 (o meglio, i suoi estremi, in questo caso i vertici che giacciono sulle due semirette sub-partizionatrici) può giacere completamente nel semispazio positivo indotto dal partizionatore corrente p1 (primo caso), oppure in quello negativo (secondo caso); i due partizionatori possono essere coincidenti, ovvero gli estremi di p2 giacciono su p1 (terzo caso), oppure p1 può dividere p2 in due parti (quarto caso). Nei primi due casi il nodo associato a p2 va passato al relativo sottoalbero del nodo associato a p1; nel terzo lo si passa al sottoalbero positivo; nel quarto il nodo va duplicato e passato ad entrambi i sottoalberi. Confrontando tutti i nodi di T2 con il medesimo nodo di T1,
dall’ albero originario T2 si ottengono due alberi da passare ai relativi sottoalberi del nodo corrente di T1. Come detto, il processo viene ripetuto per tutti i nodi di T1
fino ad arrivare alle sue foglie, nel qual caso queste ultime sono sostituite dai “frammenti” di T2 che vi giungono. L’intera operazione di filtraggio corrisponde
quindi a partizionare nuovamente le celle indotte da T2 su R attraverso i
partizionatori associati a T1. Sebbene non determinante per gli scopi di questo
algoritmo, è importante sottolineare che il filtraggio di T2 attraverso T1 è del tutto
equivalente a quello di T1 attraverso T2: sebbene gli alberi risultanti dalle due
operazioni siano diversi, essi danno luogo alla stessa descrizione dello spazio R ; si può quindi affermare che l’operazione di “filtraggio”, o più precisamente di unione, tra due alberi BSP è commutativa.
3.3 Implementazione dell’algoritmo LSP nell’EMvironment3.0
La routine che implementa l’algoritmo LSP semplificato nell’EMvironment3.0 prende il nome di LSP. Essa viene lanciata nel preprocessing dopo l’allocazione e l’inizializzazione della matrice IPS.
La struttura della routine LSP è molto simile a quella già vista per la fase di predizione, poiché molto simili sono le operazioni sottese ai due algoritmi SVBSP e LSP: ci servirà innanzi tutto una classificazione delle piastre (occlusori) per distinguere i casi particolari in cui la piramide ( ,P S Ok) presenta tre sole facce anziché quattro (cfr. Cap. 3, § 3.1.4, “Rette passanti per due segmenti”). Avremo poi bisogno di una routine che fornisca in uscita la lista ordinata front-to-back delle piastre rispetto alla piastra sorgente, o meglio rispetto al centro del top edge della piastra sorgente. Infine necessitiamo di alcune routine che costruiscano l’albero che descrive P S O( , k), ovvero il poliedro di blocco ( ,B S Ok), e che effetuino l’operazione di unione tra esso e il ROT; queste ultime routine in particolare sono molto simili alle analoghe viste per l’algoritmo SVBSP: le differenze sono minime, dovute alle differenti strutture che implementano il generico nodo dell’albero SVBSP e di quello ROT o ( ,B S Ok).
La prima operazione che va effettuata, da svolgersi una sola volta all’interno della routine, è l’inizializzazione dei campi riservati ai coefficienti dell’equazione della retta passante per il top edge della piastra nei corrispondenti elementi dell’array PIAS2D. Come vedremo, queste equazioni si rivelano molto utili alla determinazione di alcuni casi particolari.
Come precedentemente accennato, vengono quindi lanciati due cicli annidati di n loop (n è il numero di piastra che soddisfano all’ipotesi di lavoro): il primo di tali cicli seleziona la piastra sorgente, il secondo opera sulle restanti n – 1 piastre occlusori.
L’operazione svolta all’interno del secondo ciclo è la classificazione degli occlusori. Infatti non tutti questi occlusori dovranno essere elaborati, ma soltanto quelli che rispettano la condizione per la quale può verificarsi una doppia riflessione: la generica piastra occlusore k deve vedere (ed essere vista da) secondo il back/face culling la piastra sorgente. Se questa condizione è rispettata, si deve verificare che la piastra k non generi uno dei casi particolari descritti precedentemente; se non è verificata, gli elementi della matrice IPS che registrano la visibilità tra la piastra S e quella k , e viceversa, vengono posti a zero, concordemente con la simmetria imposta dal criterio PVS.
Figura 3.6 – caso particolare 1. che genera una piramide a tre sole facce
Avremo due casi particolari, che danno origine a piramidi P(S, O) degeneri:
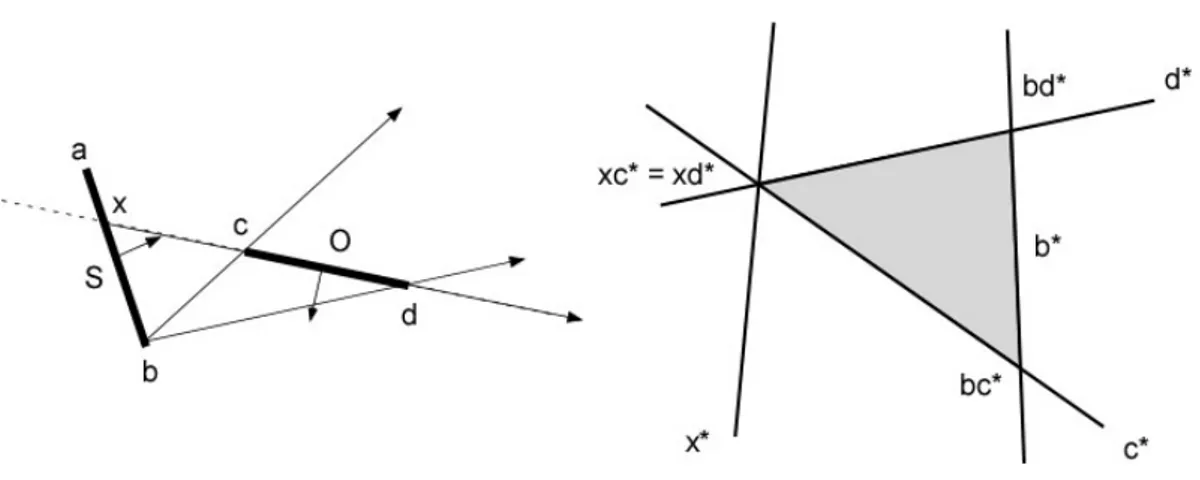
1. la retta passante per il top edge della piastra occlusore O interseca la piastra S in x ; in questo caso le rette di supporto xc e di separazione xd coincidono e di conseguenza i vertici utili per la costruzione di P(S, O) sono b, c, d (si veda la fig. 3.6).
2. la retta passante per il top edge della piastra sorgente S interseca quella O in x ; in questo caso a coincidere saranno le rette di supporto bx e di separazione ax ; i vertici utili sono a, b, c (si veda la fig. 3.7)
Figura 3.7 - caso particolare 2. che genera una piramide a tre sole facce
La classificazione delle piastre viene fatta impostando opportunamente il campo ‘sp’ nel corrispondente elemento dell’array PIAS2D; gli attributi associati ai diversi valori di ‘sp’ sono riportati nella tabella 7.
pias2d(i)%sp Attributo della piastra associata all’i-esimo elemento di PIAS2D 2 Non rispetta la condizione di doppia riflessione con la piastra sorgente 1 Rispetta la condizione di doppia
riflessione e da origine al caso particolare 2 0 riflessione e non genera nessun caso Rispetta la condizione di doppia
particolare
-1 riflessione e da origine al caso particolare 1 Rispetta la condizione di doppia Tabella 7 - attributi associati al valore del campo ‘sp’ dell’elemento pias2d(i) con l’algoritmo LSP
La verifica dell’esistenza di un caso particolare è svolta semplicemente: è sufficiente testare che i due vertici del top edge di una piastra appartengano allo stesso semipiano
tra i due indotti da una retta di riferimento; nel caso 1., la retta di riferimento sarà quella passante per O e i vertici quelli del top edge di S, viceversa nel caso 2. L’appartenenza di un vertice ad uno dei due semipiani può essere verificata andando a sostituire le cooordinate di tale vertice all’interno dell’equazione della retta di riferimento.
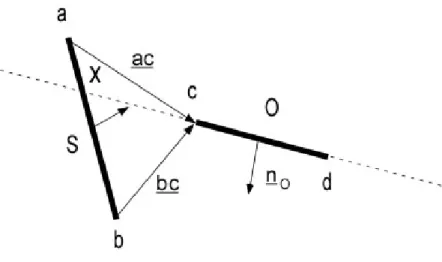
Quando per la generica piastra k si verifica il caso particolare 1., viene inizializzata la matrice REAL ‘vertexspan’ (di rango 2 e dimensione 2) all’interno del corrispondente elemento dell’array PIAS2D. In tale matrice vengono registrati gli estremi del segmento di S utili per la determinazione del poliedro di blocco ( ,B S Ok) ( i vertici x e b in fig. 3.6). Tali estremi sono identificati attraverso la conoscenza della normale della piastra k. Si prenda infatti come riferimento la fig. 3.8.
Figura 3.8 – determinazione dei vertci utili alla costruzione della piramide P(S, O)
Per la determinazione degli estremi della piastra S utili alla costruzione del poliedro di blocco ( ,B S Ok) vengono tracciati i due vettori che vanno dai vertici di S ad un vertice dell’occlusore O; scegliere un estremo di O piuttosto che un altro non modifica il risultato del metodo, per cui la scelta del vertice di O è casuale. La determinazione dell’estremo di S viene quindi effettuata controllando il segno del prodotto scalare di ognuno di questi vettori con la normale di O: data l’orientazione scelta per i vettori ac e bc in fig. 3.8, tale prodotto deve essere negativo. Gli estremi utili saranno quindi quello che soddisfa tale condizione e il punto di intersezione tra la retta passante per il top edge di O ed S (rispettivamente i punti b e x in fig. 3.8).
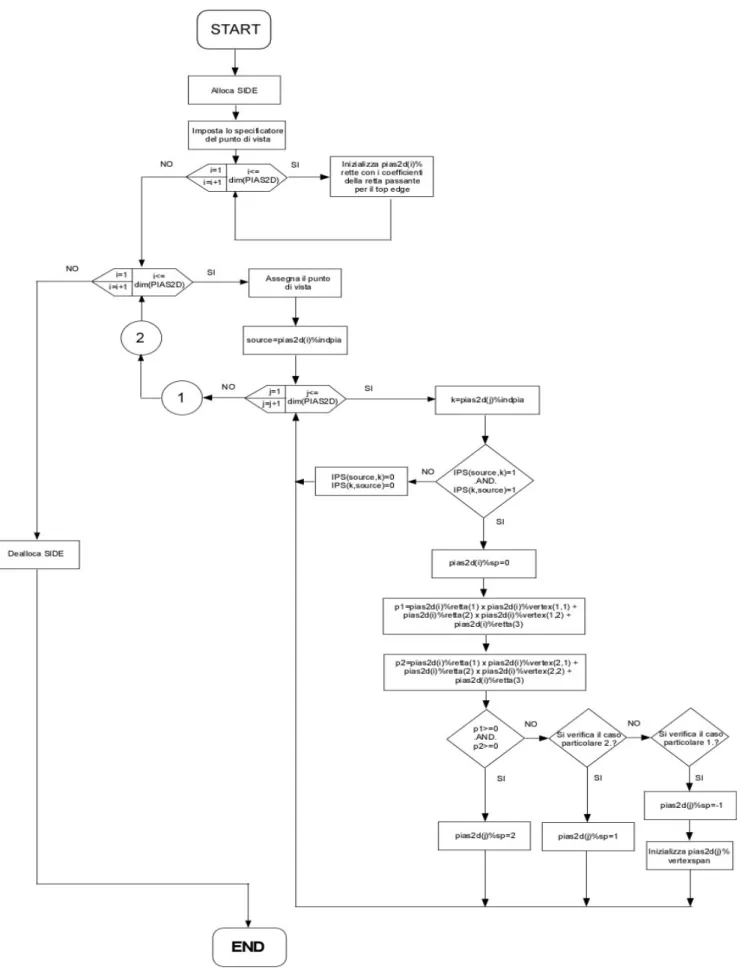
Una volta conclusa la classificazione delle piastre, si deve creare la lista ordinata front-to-back delle piastre da processare. Si è già detto che gli algoritmi LSP e SVBSP sono simili: ove possibile si è quindi cercato di usare nuovamente le routine già viste per la fase di predizione. E’ questo il caso delle procedure FRONT_TO_BACK e DISPLAY, che forniscono in uscita proprio la lista ordinata che cerchiamo (cfr. Cap 1, § 1.5.3 “Implementazione di VP”). La prima di queste due routine contiene la pseudo-procedura “pos_side” che, dato il nodo corrente all’interno dell’albero VP, determina quale sottoalbero seguire per la selezione delle piastre da inserire in lista; nel Cap. 2 si è visto inoltre che “pos_side” corrispondeva ad una semplice operazione di lettura di uno dei due array MULTI_PRIMO o MULTI_ULTIMO, concordemente con il tipo di punto di vista. Si è detto anche che nel caso dell’algoritmo LSP tale punto di vista coincide con il centro del top edge della piastra sorgente: è sembrato quindi naturale scegliere la soluzione di creare un vettore temporaneo che svolga una funzione simile a quella dei due citati, ovvero determinare per ogni piastra in quale semispazio giace il punto di vista tra i due indotti dal piano di supporto della piastra.
Allo scopo, all’inizio della routine LSP, viene quindi allocato il vettore SIDE di dimensione N pari al numero totale di piastre presenti nello scenario. Una volta scelta la piastra sorgente e assegnato come punto di vista il centro del suo top edge, quindi all’interno del primo ciclo, il vettore SIDE viene inizializzato in modo del tutto simile a quanto visto per i vettori MULTI_PRIMO e MULTI_ULTIMO attraverso la routine SIDE_VIEWPOINT. La scelta di quale vettore leggere all’interno di FRONT_TO_BACK, come già visto per la fase di predizione, viene effettuata attraverso un argomento che specifica il tipo di punto di vista. Inoltre il vettore SIDE verrà riscritto ad ogni cambio della piastra sorgente e sarà infine deallocato al temine della routine.
Per quanto riguarda la procedura DISPLAY, rispetto a quanto visto nel capitolo 2, è stata modificata aggiungendo del codice appositamente per la routine LSP: anch’essa quindi necessita di uno specificatore sulla routine che la invoca; tale specificatore coincide con quello del punto di vista.
DISPLAY contiene le condizioni per la selezione della piastre da aggiungere alla lista ordinata. Nel caso della routine LSP, la generica piastra k viene selezionata se il campo ‘sp’ nel corrispondente elemento dell’array PIAS2D contiene un valore intero compreso tra 1 e –1 (cfr. Tabella 7): viene quindi allocato un nuovo elemento da aggiungere in lista. Se ‘sp’ è pari a –1 o 0, tale elemento viene inizializzato con le informazioni contenute nel nodo corrente di VP; se ‘sp’ è uguale a 1, la piastra k da origine al caso particolare 2. e quindi si deve verificare che il frammento del suo top edge registrato nel nodo corrente di VP sia attraversato dalla retta di riferimento passante per il top edge di S. Se avviene ciò, l’elemento da aggiungere in lista andrà inizializzato con le coordinate dei vertici utili per la costruzione di ( ,B S Ok)(i vertici x e c in fig. 3.7); questa operazione è svolta in modo del tutto simile a quanto visto per il caso particolare 1. Inoltre viene impostato su .TRUE. il campo ‘spanned’ dell’elemento da aggiungere in lista, per significare il verificarsi del caso particolare 2. Il campo ‘spanned’, come vedremo tra poco, serve infatti a determinare il tipo di albero ( ,B S Ok) da costruire.
Una volta ottenuta la lista ordinata delle piastre, esse vengono processate una alla volta. Per ognuna di esse viene costruito il relativo poliedro di blocco ( ,B S Ok) attraverso la chiamata della routine CREA_ROTELEM; essa ha tra i suoi argomenti due matrici di dimensione 2x2, EDGE_SOURCE e EDGE_TARGET, che registrano le coordinate dei vertici utili, rispettivamente della piastra sorgente e dell’occlusore, per la costruzione di ( ,B S Ok). La pseudo codifica della routine è riportata di seguito.
SUBROUTINE crea_rotelem(edge_source, edge_target, root: radice dell’albero, ind: puntatore all’elemento corrente della lista delle piastre)
! “piani” e “punti” sono due matrici REAL di dimensione 4x3 che memorizzano ! rispettivamente i coefficienti dell’equazione dei piani di supporto delle facce della piramide ! P(S,O) e le coordinate dei vertici della piramide.
CALL calcola_coefficienti_piani(edge_source, edge_target, piani) CALL calcola_coordinate_vertici(edge_source, edge_target, punti) CALL orienta_piani(piani, punti)
Il calcolo dei coefficienti dei piani di supporto delle facce della piramide ( ,P S Ok) e dei suoi vertici viene fatto attraverso le (7)-(8); la pseudo-routine “orienta_piani” imposta il segno dei coefficienti dell’equazione dei piani in modo che le foglie interne dell’albero ( ,B S Ok) corrispondano alla regione di spazio interna alla piramide. Questa operazione può essere svolta grazie alla conoscenza a priori della struttura di ( ,P S Ok). Con riferimento alla fig. 3.3, sappiamo ad esempio che i vertici bc* e bd* giacciono sul piano b* e che quelli ac* e ad* si trovano invece sul piano a* ; dovremo quindi impostare il segno dei coefficienti di a* in modo che i punti bc* e bd* cadano all’interno del suo semispazio positivo, e analogamente dovremo fare con i vertici ac* e ad* per i coefficienti di b*. L’operazione viene ripetuta anche per i restanti piani c* e d*.
! “a” è l’indice dell’elemento dell’array “pias2d” relativo alla piastra in elaborazione, “c” ! una variabile di appoggio
IF (ind%spanned=.TRUE.) THEN C = 1
ELSE IF (pias2d(a)%sp=-1) THEN C = 2
ELSE C = 0 ENDIF
! “app” è un puntatore di appoggio SELECT CASE (C)
CASE(0)
DO i=1, 4
ALLOCATE(nuovo_nodo)
CALL inizializza(nuovo_nodo, piani, punti) IF (.NOT.(ASSOCIATED(root))) THEN root=>nuovo_nodo app=>nuovo_nodo ELSE app%pos=>nuovo_nodo app=>nuovo_nodo ENDIF END DO CASE(1,2) DO i=1, 3 ALLOCATE(nuovo_nodo) CALL inizializza(nuovo nodo, piani, punti)
Orientati i piani, si può costruire iterativamente attraverso un unico ciclo l’albero ( , k)
B S O , allocandone e inizializzandone opportunamente i nodi e ponendo ogni nuovo nodo nel sottoalbero positivo del precedente. Tale costruzione non può prescindere dalla classificazione della piastra in elaborazione: si hanno infatti tre diversi cicli (selezionati in CREA_ROTELEM attraverso il costrutto select case di argomento la variabile ‘c’), corrispondenti al verificarsi di uno dei tre casi visti precedentemente (il caso generale e i due particolari che danno origine a piramidi degeneri). Le istruzioni per una corretta costruzione di ( ,B S Ok) sono contenute all’interno della pseudo-routine “inizializza” che assegna ai campi del nodo allocato gli opportuni coefficienti del piano e le coordinate dei vertici che giacciono sopra di esso, secondo lo schema riportato nelle fig. 3.3-3.4; essa provvede anche ad inserire nell’ultimo nodo dell’albero il primo elemento della lista degli ostacoli associati alla regione di spazio descritta da ( ,B S Ok): tale elemento corrisponde alla piastra stessa.
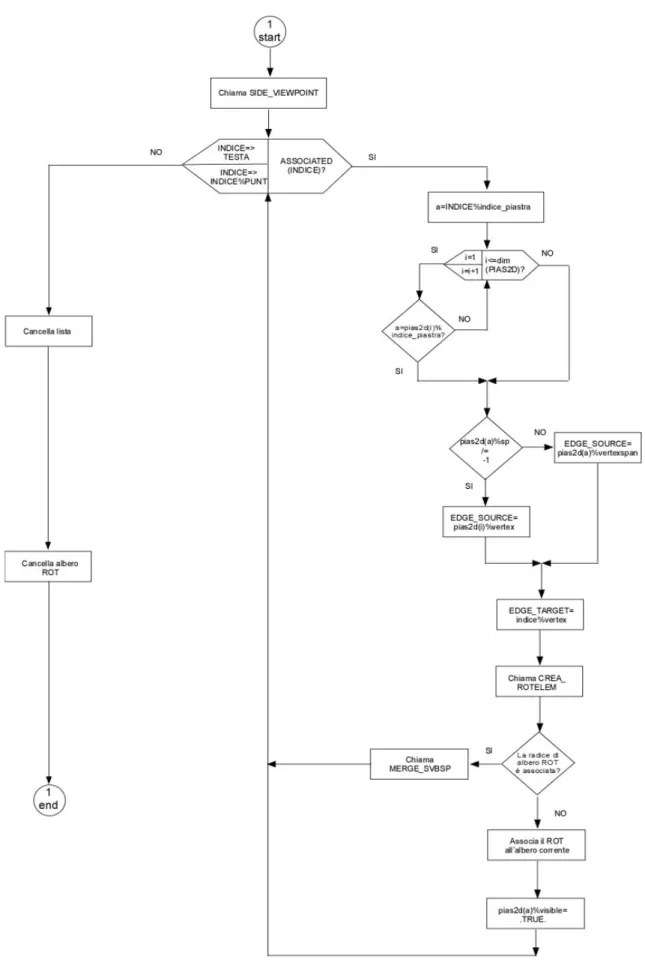
Una volta creato il poliedro di blocco, si verifica che la radice del ROT sia dissociata, nel qual caso la piastra in elaborazione è la prima ad essere processata e quindi risulta sicuramente visibile: viene posto .TRUE. il campo ‘visible’ nel corrispondente elemento dell’array PIAS2D. Nel caso in cui invece la radice dell’albero ROT sia già associata, ( ,B S Ok) viene invece filtrato attraverso di esso. La routine ricorsiva che compie questa operazione prende il nome di MERGE_ROT; la pseudo-codifica è riportata oltre.
Come già accennato, la struttura di MERGE_ROT è piuttosto simile a quella di MERGE_SVBSP già vista nel Cap. 2: le funzioni che ambedue svolgono (verifica della visibilità di una piastra, aggiornamento di un albero BSP) sono infatti le stesse. La differenza risiede nel fatto che mentre nella seconda ad essere “filtrato” attraverso un albero era un segmento, nella prima è un altro albero, secondo il procedimento descritta nel paragrafo 3.2 .
La routine PARTIZIONA_ROT scompone l’albero ( ,B S Ok) in due alberi distinti grazie al partizionatore contenuto nel nodo corrente del ROT; questi alberi vengono passati ai relativi sottoalberi del nodo corrente del ROT, e il procedimento viene ripetuto per ogni nodo del ROT fino a che non si giunge in una foglia esterna o in una interna; nel primo caso l’occlusore è visibile e il ROT viene aggiornato, nel secondo viene invocata la routine CFR_ALTEZZA, identica a quella descritta nel Cap.2, per eseguire il controllo sull’altezza dell’occlusore. Se l’esito è positivo, la piastra viene assunta visibile e un nuovo elemento viene aggiunto alla lista degli
RECURSIVE SUBROUTINE merge_rot (nt1: nodo corrente del ROT; nt2: radice di B(S,O); indice: puntatore all’elemento corrente della lista della piastre)
! “split_in” è il puntatore alla parte di B(S,O) da passare al sottoalbero positivo di nt1 ! “split_ext” è il puntatore alla parte di B(S,O) da passare al sottoalbero negativo di nt1 CALL partiziona_rot(nt1, nt2, split_in, split_ext)
IF (ASSOCIATED(split_ext)) THEN nt2=>split_ext
IF (ASSOCIATED(nt1%neg)) THEN
CALL merge_rot(nt1%neg, indice, nt2) ELSE
! aggiorno l’albero ROT
! ‘a’ è l’indice dell’elemento dell’array “pias2d” associato alla piastra nt1%neg=>split_ext pias2d(a)%visible=.TRUE. ENDIF ENDIF IF (ASSOCIATED(split_in)) THEN nt2=>split_in IF (ASSOCIATED(nt1%pos)) THEN CALL merge_rot(nt1%pos, indice, nt2) ELSE
! visible è la variabile locale che classifica la visibilità del segmento nella cella visible=.FALSE.
CALL cfr_altezza(nt1%lista_ostacoli, indice, visible) IF (visible) THEN
! aggiunge un nuovo nodo alla lista degli ostacoli
CALL aggiungi_nodo(nt1%lista_ostacoli, indice) pias2d(a)%visible=.TRUE. ENDIF CALL erase_rot(nt2) ENDIF ENDIF END SUBROUTINE
ostacoli presenti nella foglia, altrimenti la piastra risulta invisibile. Terminato il controllo dell’altezza, il frammento di ( ,B S Ok) arrivato nella cella interna viene cancellato.
La pseudo-codifica di PARTIZIONA_ROT è riportata nella pagina successiva. Come si può notare, questa routine esegue delle operazioni più volt descritte: verifica a quale semispazio tra i due indotti dal nodo corrente n1 del ROT appartengono i due vertici del nodo corrente n2 di ( ,B S Ok)andando a sostituire le loro coordinate all’interno dell’equazione del piano partizionatore di n1. Se entrambi appartengono al semispazio positivo, il nodo viene inserito nell’albero da passare al sottoalbero positivo (la cui radice è “split_in”), viceversa in quello da passare al sottoalbero negativo (“split_ext”); se i due vertici appartengono invece a due semispazi differenti, viene calcolato la retta intersezione dei due piani partizionatori contenuti in n1 e n2. Su tale retta giace il nuovo vertice, che come detto è assunto essere l’intersezione tra la retta e la sfera di raggio unitario. A questo punto il nodo originale può essere duplicato e passato ad entrambi gli alberi (“split_in” e “split_ext”).
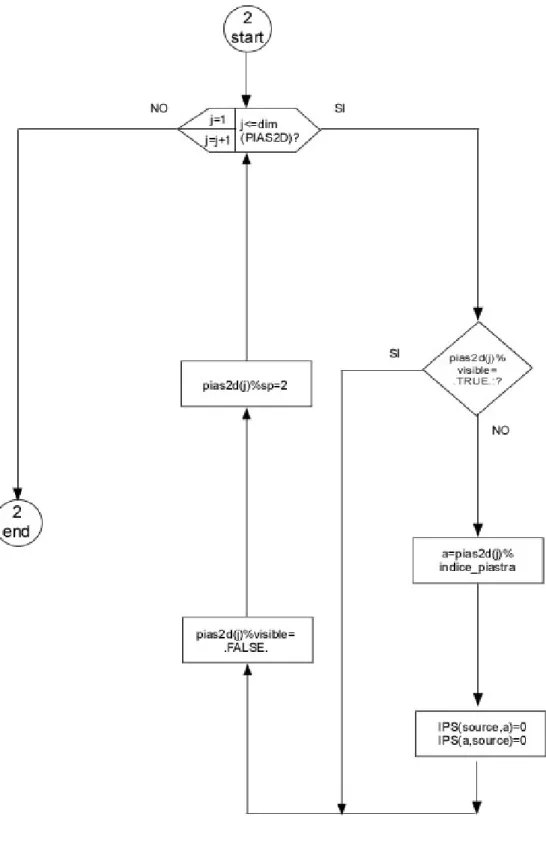
Una volta filtrato il poliedro di blocco ( ,B S Ok), si passa alla piastra occlusore successiva e si ripete il procedimento. Terminata la scansione della lista ordinata, viene fatta un nuovo ciclo sulle piastre per verificare quali sono risultate visibili e quali non visibili. Il valore registrato negli elementi di IPS relativi alla visibilità tra la sorgente S e una piastra k, e viceversa, viene posto a zero soltanto se la piastra è risultata essere invisibile, altrimenti viene lasciato inalterato. Nello stesso ciclo vengono reimpostati su 2 i campi ‘sp’ e .FALSE. i campi ‘visible’ dell’array PIAS2D. Terminato il ciclo, viene scelta una nuova piastra sorgente e la procedura si ripete, fino a che ogni piastra non è stata scelta a sua volta come sogrgente.
SUBROUTINE partiziona_rot(split_in, split_ext, nt1: puntatore al nodo corrente del ROT; nt2:radice dell’albero da filtrare)
! sweep è un puntatore di appoggio sweep=>nt2
DO
IF (.NOT.(ASSOCIATED(sweep))) EXIT
ris1=nt1%coeff(1)*sweep%vertice1(1)+ nt1%coeff(2)*sweep%vertice1(2)+ nt1%coeff(3)*sweep%vertice1(3)
ris2= ris1=nt1%coeff(1)*sweep%vertice1(1)+ nt1%coeff(2)*sweep%vertice1(2)+ nt1%coeff(3)*sweep%vertice1(3)
IF (ris1>0 .AND. ris2>0) THEN
CALL aggiungi_nodo(sweep, split_in) ELSE IF IF (ris1<0 .AND. ris2<0) THEN
CALL aggiungi_nodo(sweep, split_ext) ELSE
! “nuovo_vertice” è l’array che contiene le coordinate del nuovo vertice CALL intersezione_piani(nt1, nt2, nuovo_vertice) ALLOCATE(nuovo_nodo)
CALL inizializza_nodo(nuovo_nodo, sweep, nuovo_vertice) CALL aggiorna_nodo(sweep, nuovo_vertice)
CALL aggiungi_nodo(split_in, sweep) CALL aggiungi_nodo(split_ext, nuovo_nodo) ENDIF
sweep=>sweep%punt END DO