INDICE
INTRODUZIONE
………....pag. 04
CAPITOLO I: Teoria della simulazione analitica
1.1. Configurazioni caratterizzabili con DJOSER………..……..…pag. 11
1.2. Formulazione teorica………...……pag. 15
1.3. Formulazione algebrica………...…..pag. 23
1.4. Esempi di simulazione……….………...pag. 29
CAPITOLO II: Prove sull’accuratezza della
simulazione analitica
2.1. Confronto con simulazione FEM……...………..….pag. 35
2.2. Discussione sull’accuratezza…………...……….….…pag. 40
CAPITOLO III: Validazione sperimentale I
3.1. Costruzione dei campioni………..pag. 48
3.2. Misurazione ………...pag. 54
3.3. AVA………..pag. 58
3.4. AAVRA……….pag. 71
3.5. AMAMR………...pag. 82
CAPITOLO IV: Validazione sperimentale II
4.1. Applicazione di DJOSER a circuiti di potenza……….pag. 96
INTRODUZIONE
L’oggetto di questa tesi è una nuova strategia di simulazione termica in regime stazionario, denominata DJOSER, particolarmente, ma non esclusivamente, dedicata ai sistemi di assemblaggio dei dispositivi elettronici di potenza.
La previsione dell’assetto termico dei dispositivi e e dei sistemi elettronici è una esigenza stringente ed irrinunciabile per garantire l’affidabilità del prodotto., L’intensificarsi attuale del problema termico è indotto dalla tendenza progressiva della riduzione delle dimensioni dei dispositivi ed all’aumento in generale del grado di integrazione. Un corretto dimensionamento circuitale che tenga conto degli effetti termici infatti permette una maggiore affidabilità, un tempo di vita medio, una velocità ed una robustezza di prestazioni del dispositivo stesso. Si prevede dunque che l’analisi termica diventerà uno dei principali settori di investimento per le aziende del settore, con un incremento che si sta già osservando oggi.
Per questi dispositivi la tecnica DJOSER è appunto proponibile, a parità di accuratezza, in luogo degli usuali programmi basati sul metodo di calcolo agli elementi finiti (FEM). Questi ultimi infatti rischiano di essere troppo oneroso per aziende di piccolo e medio livello, per le quali il costo d’un programma basato sul FEM e i mezzi hardware sufficienti per gestirne l’elaborazione diventano eccessivi. Oltre a ciò i simulatori FEM comportano un’alta specializzazione del personale addetto al loro utilizzo, con una conoscenza consistente da parte di quest’ultimo del modello matematico utilizzato e con dunque costi aggiuntivi per la formazione del personale stesso.
La tecnica DJOSER è applicabile a strutture assimilabili ad una sequenza di strati omogenei sovrapposti1 simili ad una piramide a gradoni, eventualmente asimmetrica, e dove le potenze dissipate siano riconducibili a sorgenti termiche bidimensionali distribuite sulle interfacce tra gli strati. Inoltre è stata inserita una vasta gamma di
condizioni al contorno e di tipologie di potenze dissipate in modo da rendere i modelli quanto più possibile vicini alle strutture tipiche delle moderne tecnologie di montaggio. Le distribuzioni di flusso e di temperatura sono ottenute da un sistema di equazioni integrali direttamente traducibile, tramite le usuali tecniche di quadratura, in un sistema algebrico lineare. Grazie all’uso di reticoli 2-D, anziché 3-D, per la descrizione delle grandezze termiche, e la conseguente riduzione di incognite, si ottiene un sistema di simulazione che, almeno per i dispositivi elettronici di potenza, è in grado di competere con programmi FEM per ridotto volume di calcolo. Le fonti di minor accuratezza risiedono nella procedura di calcolo ovvero nel troncamento delle serie armoniche infinite, connesse con le funzioni di Green, e le dimensioni delle griglie bidimensionali con cui vengono descritte le funzioni di temperatura e flusso ed utilizzate per il calcolo numerico degli integrali di superficie.
I dati forniti dal simulatore DJOSER confrontati con quelli ottenuti da un programma basato sulla tecnica di calcolo agli elementi finiti mostrano comunque un’accuratezza della temperatura contenuta entro l’1%. Il risparmio nel tempo di elaborazione, per converso, è notevole, oltre il 10%, ed è l’aspetto più interessante per chi progetta dispositivi elettronici di potenza, in quanto DJOSER rappresenta uno strumento flessibile, accurato e veloce per la simulazione.
In altre parole DJOSER si propone come uno strumento alternativo agli attuali simulatori FEM, competitivo con essi per costo e prestazioni. Esso è stato pensato per essere utilizzato anche su elaboratori di media potenza necessitando di un tempo di elaborazione significativamente minore, grazie alle soluzioni matematiche e alle condizioni al contorno imposte. Oltre a ciò l’altro vantaggio risiede nella semplificazione di interfacciamento con l’utilizzatore, in quanto, per come è strutturato DJOSER, non occorrono competenze matematiche specifiche per il suo utilizzo, dal momento in cui all’utente è affidato solo la creazione della struttura da esaminare, la conoscenza dei parametri di processo, ovviamente, e la scelta dei parametri d’uso di DJOSER in base alla geometria e alle caratteristiche termiche dei materiali utilizzati. In base a questo è compito dell’utilizzatore scegliere il passo della griglia da applicare alla
struttura e il numero di autovalori da prevedere nel calcolo. Per il resto la composizione della struttura è automatica.
Per inciso questo tipo di analisi permette, in fase di progettazione, un migliore utilizzo della struttura stessa e un’ottimizzazione delle prestazione, evitando un sovradimensionamento delle strutture che attualmente spesso sopperisce alla scarsa accuratezza dell’analisi termica stessa.
La tesi si sviluppa partendo dall’esposizione delle soluzione teoriche ed analitiche proposte da DJOSER che consentono di ricondurre il problema alla risoluzione di un sistema lineare di dimensioni inferiori rispetto al FEM. A questo punto si rende necessario confrontare le prestazioni in termini di velocità ed accuratezza DJOSER rispetto a FEM, ottenendo un errore al di sotto dell’1% e una velocità superiore al 10%. Verrà oltre a ciò discussa l’accuratezza di DJOSER in funzione della scelta del passo della griglia e del numero di autovalori per una struttura campione.
Dopo ciò abbiamo convalidato sperimentalmente quanto sopra dimostrato nella teoria con tre coppie di campioni. Ogni coppia è costituita da un sistema monodimensionale ed un modello a piramide. Il modello monodimensionale è stato utile per individuare i parametri di processo, come le resistenze termiche di contatto e la conducibilità di alcuni materiali utilizzati, in quanto la monodimensionalità ci permette di poter considerare il flusso termico normale alle superfici e nullo il trasporto per convezione. Per caratterizzare i materiali abbiamo proceduto a fare misurazioni di temperatura con una sonda RTD al platino.
Abbiamo infine compiuto misurazioni termografiche sulle strutture piramidali con una telecamera a raggi infrarossi AVIO Neo Thermo TVS-600 ed abbiamo confrontato i profili di temperatura rilevati dalla telecamera lungo due piani traversi con quelli simulati da DJOSER, osservando una sostanziale analogia e confermando pertanto la bontà della simulazione stessa.
L’ultima prova è stata compiuta su un dispositivo di potenza, un regolatore prodotto da MITSUBA EUROPE, ottenendo la medesima accuratezza.
1. CAPITOLO I
TEORIA DELLA SIMULAZIONE
ANALITICA
1.1. Configurazioni caratterizzabili con DJOSER…………..…pag. 11
1.4. Formulazione teorica………..……pag. 15
1.5. Formulazione algebrica………..pag. 23
1.6. Esempi di simulazione………....pag. 29
1.1 CONFIGURAZIONI CARATTERIZZABILI CON DJOSER
Il programma DJOSER risponde alla necessità di caratterizzazione termica dei dispositivi elettronici in fase di progettazione. Questo impone la ricerca di soluzioni software capaci di coniugare accuratezza nell’analisi termica dei dispositivi e onerosità delle soluzioni stesse.
Una possibile soluzione ci è porta dal ben noto metodo agli elementi finiti (FEM), che è adattabile a qualsiasi tipo di geometria. Essa sostanzialmente si basa sulla discretizzazione delle equazioni che descrivono la conduzione termica all’interno di una fitta rete di elementi solidi. Perciò questo tipo di analisi necessita di un accoppiamento in 3D della struttura la quale, in genere, non è uniforme; la complessità di tale procedura è evidente. In aggiunta a ciò dobbiamo considerare che le capacità di dissipazione termica di un sistema sono dovute sia al package del singolo dispositivo, sia a quanto ad esso connesso dall’utilizzatore o da un secondo produttore, al fine di realizzare il sistema voluto. Pertanto la temperatura massima all’interno del sistema complessivo è ricavata da più passi di processo, e può accadere che vengano utilizzati differenti metodologie di analisi e dunque differenti gradi di accuratezza. Si rende pertanto necessario un sistema di simulazione, utilizzabile sia dai produttori sia dagli utilizzatori di sistemi singoli o composti, economico, che richieda il minor tempo possibile di elaborazione, con ottima accuratezza del risultato.
Di qui l’esigenza di uno strumento di simulazione come DJOSER. Molti dei dispositivi utilizzati in elettronica infatti possono essere descritti come pile di strati omogenei di differenti materiali, connessi per sovrapposizione o attraverso l’ausilio di sottili saldature o strati di materiale adesivo.
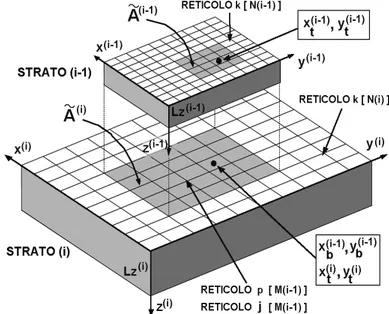
La dissipazione di potenza può essere assunta in 2D su una o più interfacce con la faccia in basso connessa al pozzo termico o direttamente o attraverso uno strato con coefficiente di convezione termica noto. Queste strutture, come mostrato nella fig. 1.1.1 sono pensate costituite da parallelepipedi a facce regolari, di varia altezza, e collocati l’uno sull’altro con spigoli paralleli. Ogni generico prisma della struttura è pensato fisicamente omogeneo ed ha il rettangolo di base di dimensioni inferiori rispetto al prisma su cui è poggiato e maggiori di quello che esso sostiene. Ne risulta una sorta di piramide a gradoni di varia altezza, per la quale non sono necessariamente individuabili piani di simmetria.
Preso in esame un singolo strato (fig. 1.1.2) definiamo con qˆ(x,y)e Tˆ(x,y) sono rispettivamente il flusso termico proveniente dallo strato soprastante e la distribuzione di temperatura dell’area di contatto con lo strato sottostante [5,6]. Ovviamente lo strato in cima alla pila presenterà qˆ(x,y)nullo, mentre lo strato inferiore presenterà una
FIG 1.1.1 Esploso della sezione traversa di un dispositivo elettronico con visualizzati i suoi elementi resistivi e gli elementi di generazione
FIG 1.1.2 Schematizzazione di un generico prisma parallelepipedo costituente la struttura, in cui sono segnati i parametri termici.
che riprenderemo più ampiamente nella trattazione teorica seguente, su cui si basa lo DJOSER è quella di superfici laterali adiabatiche. In altre parole ammettiamo che se sono presenti fenomeni convettivi, essi sono localizzati sulle superfici orizzontali in contatto con l’ambiente esterno. Ciò permette di poter considerare il sistema in 2D, riducendo drammaticamente il numero di variabili in gioco e dunque la complessità delle equazioni che il processore deve risolvere, con una conseguente riduzione dei tempi di elaborazione. Oltre a ciò tutti gli accoppiamenti fra superfici bidimensionali possono essere resi uniformi utilizzando superfici quadrate della stessa area; ciò rende possibile una implementazione completamente automatica delle fasi di pre-processo e di costruzione del modello da esaminare. Queste peculiarità rendono questo strumento di simulazione analitica capace di interagire con programmi CAD per la progettazione tanto dei dispositivi elettronici quanto del loro assemblaggio. Un altro importante aspetto dello DJOSER è che, grazie alla velocità e alla minor complessità di elaborazione, è particolarmente adatto per la simulazione di cicli termo-elettrici basati sull’interazione mutua fra le caratteristiche elettriche dei dispositivi e distribuzioni di temperatura.
Un esempio tipico dell’utilizzo di DJOSER è il fenomeno chiamato “hot-spot” nei transistori bipolari di potenza [1,2]. Può essere comunque usato per sistemi elettronici planari e può essere utilizzato nell’analisi di un’ampia gamma di configurazioni, come circuiti incapsulati in package, dispositivi che supportano flip-chip o BGA, circuiti ibridi, schede elettroniche stampate con tecnologia di superficie o su substrati per l’interconnessione di multistrati metallici.
fig. 1.1.3 flip-chip packaging ASPEN Tecnologies
L’unico requisito è che la dissipazione di potenza attiva deve avvenire in due dimensioni, non volumetrica, e deve essere localizzata sulla superficie in cima alla pila, oppure all’interfaccia fra due strati. Ipotesi queste facilmente verificabili in molti casi pratici. Nel caso lavorassimo con strati sepolti possiamo pensare di dividere l’analisi della singola pila in quella di più pile consecutive.
Abbiamo supposto l’omogeneità dei materiali. Se questa venisse a mancare, ovvero se i materiali presentassero proprietà termiche non uniformi lungo il piano orizzontale, se fossero sagomati profili per aumentare la dissipazione, se fossero presenti piedinature esterne di integrati incapsulati, o se gli stessi materiali presentassero coefficienti di resistività non omogenei, lo DJOSER non offre risultati accurati.
fig. 1.1.5 esempio di metallizzazione multistrato
saldatura
incollaggio
To To To
Ta
1.2 TRATTAZIONE TEORICA
Prendiamo ad esempio una struttura piramidali multistrato.
L’analisi termica dell’intera struttura si basa sulla conoscenza della soluzione di un problema di conduzione termica, in regime stazionario, formulato per un generico parallelepipedo, imponendo sulle facce di ogni strato della pila le condizioni al contorno convettive opportune. Abbiamo infatti detto che l’ipotesi di applicabilità dello strumento DJOSER risiede nel poter considerare sulle facce laterali uno scambio di calore per convezione con un ambiente a temperatura costante in cui la struttura è collocata. Per semplicità assumiamo la temperatura ambiente come zero di riferimento, di modo che le condizioni al contorno sulle facce laterali risultino lineari omogenee del terzo genere [3]. Anche per le basi della struttura a pila assumiamo uno scambio convettivo, ma essendo la temperatura esterna all’interfaccia in generale variabile da punto a punto, le condizioni da porre sono ancora del terzo genere, ma non più omogenee.
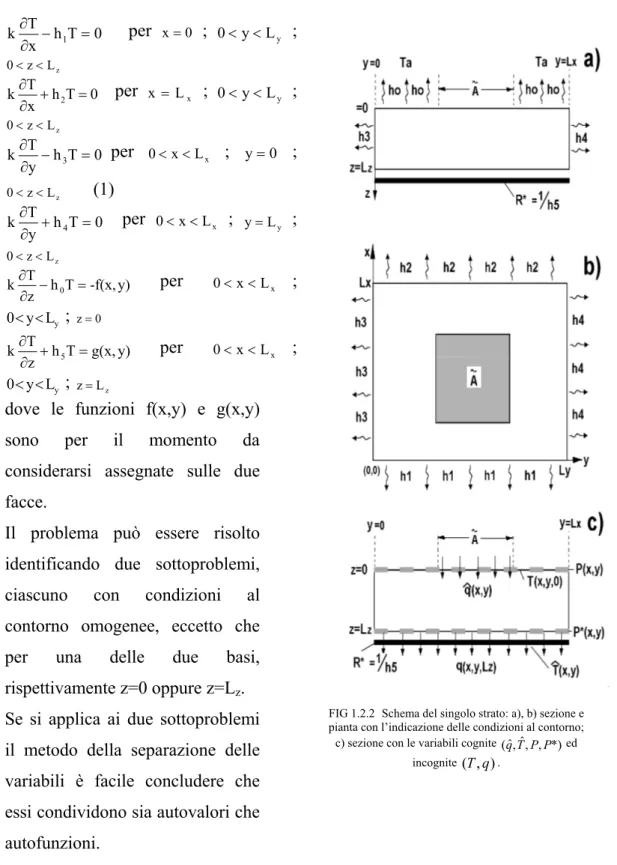
Analizziamo adesso un singolo strato: data la geometria prismatica il sistema di riferimento più comodo risulta quello in coordinate rettangolari. Il problema risulta analiticamente così impostato:
0 T= ∇2 per x L x 0< < ; 0<y<Ly ; z L z 0< <
FIG 1.2.1 Struttura piramidale multistrato asimmetrica in cui sono presenti strati di incollaggio e saldatura. La base è a contatto col pozzo di temperatura To eventualmente non
0 T h x T k ∂ − 1 = ∂ per 0 x= ; 0<y<Ly ; z L z 0< < 0 T h x T k + 2 = ∂ ∂ per x L x = ; 0<y<Ly ; z L z 0< < 0 T h y T k ∂ − 3 = ∂ per x L x 0< < ; y=0 ; z L z 0< < (1) 0 T h y T k + 4 = ∂ ∂ per x L x 0< < ; y=Ly ; z L z 0< < y) -f(x, T h z T k − 0 = ∂ ∂ per x L x 0< < ; y L y 0< < ; z=0 y) g(x, T h z T k + 5 = ∂ ∂ per x L x 0< < ; y L y 0< < ; z=Lz
dove le funzioni f(x,y) e g(x,y) sono per il momento da considerarsi assegnate sulle due facce.
Il problema può essere risolto identificando due sottoproblemi, ciascuno con condizioni al contorno omogenee, eccetto che per una delle due basi, rispettivamente z=0 oppure z=Lz.
Se si applica ai due sottoproblemi il metodo della separazione delle variabili è facile concludere che essi condividono sia autovalori che autofunzioni.
In particolare, una volta introdotte le grandezze adimensionali note come numeri di Biot:
FIG 1.2.2 Schema del singolo strato: a), b) sezione e pianta con l’indicazione delle condizioni al contorno; c) sezione con le variabili cognite (qˆ,Tˆ,P,P*) ed
y 4 3 x 2 1 z 5 0 j j L L L , L L L , L L L dove k / L h Bi(j) = = = = = = =
gli autovalori per Bi(j)+Bi(j+1)≠0 sono soluzioni della seguente equazione trascendente ξ 1)] Bi(j [Bi(j) 1) Bi(j Bi(j) 1) Bi(j Bi(j) ξ ) ctg( + + + ⋅ − + + = ξ (3) mentre per Bi(j)+Bi(j+1)=0 sono invece
1)π ,...(n 3π , 2π , π 0, ξ = − .
Le corrispondenti autofunzioni risultano
y) (µ sen Bi(3) y) cos(µ L µ y) Y(µ x) (β sen Bi(1) x) cos(β L β x) X(β m m y m m n n x n n + = + = (4) e le rispettive norme sono [4]:
[
]
[
]
[
]
[
]
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + ⋅ + = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + ⋅ + = Bi(3) Bi(4) ) L (µ Bi(4) 1 Bi(3) ) L (µ 2 1 ) N(µ Bi(1) Bi(2) ) L (β Bi(2) 1 Bi(1) ) L (β 2 1 ) N(β 2 2 y m 2 2 y m m 2 2 x n 2 2 x n n (5)A partire dalle autofunzioni, e in accordo con le loro ben note proprietà di ortogonalità, si costruisce la soluzione [3] che contiene una serie doppia relativa allo sviluppo di Fourier della funzione f(x,y) o g(x,y), a seconda della base dove è posta la condizione al contorno non omogenea a cui il sottoproblema si riferisce. La somma delle due soluzioni è infine la soluzione del problema di partenza. Ponendo
(
)
[
υ L Bi(0) Bi(5)]
sinh(υ L )[
Bi(0) Bi(5)]
(
υ L)
cosh(υ L )m) S(n, µ β υ z m n, z m n, z m n, 2 z m n, 2 m 2 n m n, ⋅ + + ⋅ ⋅ + = + = (6) la soluzione risulta la seguente:
[
]
[
]
∑∑
∞ = ∞ = ⋅ ⎩ ⎨ ⎧ + ⋅ ⋅ ⋅ = 1 n m1 z m n, z m n, z m n, m n m n z m) S(n, z) -(L υ Bi(5)sinh z) -(L υ cosh L υ ) N(µ ) N(β y) Y(µ x) X(β k L z) y, T(x, n n x m m y j 1 ξ β L j 3 ξ µ L = = = = (2)⎪⎭ ⎪ ⎬ ⎫ ′ ′ ′ ⋅ ′ ⋅ ′ ′ ⋅ ⋅ + + ′ ′ ′ ′ ′ ′
∫ ∫
∫ ∫
Lx 0 Ly 0 m n y x m n, m n, z m n, Lx 0 Ly 0 m n y x y d x d ) y Y(µ ) x X(β ) y , x g( L L 1 m) S(n, z) υ Bi(0)sinh( z) cosh(υ L υ y d x d ) y )Y(µ x )X(β y , x f( L L 1 (7)Quindi trasferendo alla struttura piramidale il risultato relativo ad un elemento, innanzitutto si devono individuare le funzioni f(x,y) e g(x,y) a partire dalla schematizzazione fisica della struttura.
Mentre sulle facce laterali di un generico elemento prismatico si ha scambio termico convettivo con l’ambiente esterno, sulle basi possono in generale essere presenti
• sulla base z=0: una sorgente piana di generazione di calore per unità di superficie e di tempo dovuta per esempio all’effetto Joule; il flusso termico specifico che, attraversando l’interfaccia di contatto Ã, proviene dall’elemento sovrapposto a quello in esame; lo scambio convettivo di calore presente solo sulla parte (A−A~) della superficie di base a diretto contatto con l’ambiente
esterno;
• sulla base z=Lz : lo scambio di calore per conduzione verso l’elemento
sottostante con l’eventuale presenza di una resistenza di contatto tra i due elementi; in presenza della suddetta resistenza di contatto una ulteriore sorgente piana di generazione di calore per unità di superficie e di tempo.
Dal punto di vista analitico la maggiore difficoltà sorge sulla base superiore z=0 dell’elemento prismatico dove, in accordo a quanto abbiamo detto, si hanno condizioni al contorno miste: una del secondo genere su (x,y)∈ e l’altra del terzo genere su A~
) A (A y) (x, ∈ −~ [3]. Se si indica con:
• P(x,y) la generazione piana di calore dovuta per esempio all’effetto Joule connesso al passaggio di corrente in giunzioni tra semiconduttori o a cadute ohmiche su piste metallizzate
• qˆ(x, y)il flusso termico proveniente dall’elemento sovrastante, nullo per ) A (A y) (x, ∈ − ~
• T(x,y,0) la temperatura sulla base superiore dell’elemento prismatico in esame allora la funzione f(x,y) sulla base z=0 sarà data da
y,0) T(x, h y) (x, q y) P(x, y) f(x, = +ˆ + 0 per (x,y)∈A~ , z=0 y) P(x, y) f(x, = per (x,y)∈(A−A~) ; z =0 (8) In questo modo per
h
0≠
0
la condizione al contorno relativa alla faccia z=0 implicherà uno scambio convettivo identicamente nullo sulla parte (x,y)∈A~ e non nullo con l’ambiente a temperatura zero sulla parte restante (x,y)∈(A−A~).Ovviamente la posizione fatta non risolve di per sé la difficoltà connessa all’esistenza di condizioni al contorno miste. Infatti, anche ipotizzando che le funzioni P(x,y) e qˆ(x,y)
siano assegnate, la temperatura T(x,y,0) rimane del tutto incognita e ciò implica che nello sviluppo in serie doppia di Fourier si presenti un’equazione integrale. Sulla base inferiore dell’elemento z=Lz la situazione è più semplice ed indicando con
• P*(x,y) la ulteriore generazione piana di calore dovuta ai fenomeni sopra citati
• Tˆ(x,y) la temperatura dell’interfaccia dell’elemento prismatico sottostante • R* la resistenza termica di contatto tra l’elemento in esame e il sottostante
la funzione g(x,y) risulta:
* * R y) (x, T y) (x, P y) g(x, = + ˆ per (x,y)∈A, z =Lz (9)
Si noti che la resistenza termica di contatto comporta uno scambio termico lineare come quello convettivo e che dunque risulta
5 h / 1
R*= (10) Dalla schematizzazione fisica della struttura con cui sono state individuate le funzioni f(x,y) e g(x,y) emerge con chiarezza che, mentre i termini di generazione piana di calore P(x,y) e P*(x,y) sono funzioni assegnate, i termini qˆ(x,y) e Tˆ(x,y) relativi rispettivamente all’interfaccia superiore ed a quella inferiore dell’elemento in esame
non sono affatto noti, ma anzi dipendono dai campi termici dell’elemento sovrastante e quello sottostante.
Per procedere nell’analisi termica della struttura piramidale, sostituiamo nella soluzione T(x,y,z), e nella sua derivata rispetto a z, le funzioni f(x,y) e g(x,y) con le (8) e (9), quindi operiamo in modo da esprimere la temperatura in z=0 ed il flusso termico in z=Lz nella forma seguente
[
]
[
]
∫∫
∫∫
∫∫
′ ′ ′ ′ ′ ′ + ′ ′ + ′ ′ ′ ′ ′ ′ + ′ ′ + + ′ ′ ′ ′ ′ ′ = A 12 A 11 z 11 A~ y d x y)d x, | y , x ( G ) y , x ( Tˆ ) y , x ( P R y d x y)d x, | y , x ( G ) y , x ( qˆ ) y , x P( k L y d x y)d x, | y , x ( G ,0) y , x T( Bi(0) y,0) T(x, * * (11a) ---[
]
[
]
∫∫
∫∫
∫∫
′ ′ ′ ′ ′ ′ + ′ ′ − ′ ′ ′ ′ ′ ′ + ′ ′ + + ′ ′ ′ ′ ′ ′ = A 22 z A 21 21 A~ 0 z y d x y)d x, | y , x ( G ) y , x ( Tˆ ) y , x ( P R L k -y d x y)d x, | y , x ( G ) y , x ( qˆ ) y , x P( y d x y)d x, | y , x ( G ,0) y , x T( h ) L y, q(x, * * (11b)dove le grandezze Gij(x’,y’|x,y) sono le funzioni di Green così di seguito strutturate, per
il caso presente: y) Y(µ x) X(β ) N(µ ) N(β ) y Y(µ ) x X(β m) S(n, m) (n, D L L 1 y) x, | y , x ( G m n m n m n 1 n m 1 11 y x 11 ⋅ ⋅ ⋅ ⋅ ′ ⋅ ′ ⋅ = ′ ′
∑∑
∞ = ∞ = (12) --- y) Y(µ x) X(β ) N(µ ) N(β ) y Y(µ ) x X(β m) S(n, Bi(5) L υ L L 1 y) x, | y , x ( G m n m n m n 1 n m 1 z m n, y x 12 ⋅ ⋅ ⋅ ⋅ ′ ⋅ ′ ⋅ = ′ ′∑∑
∞ = ∞ = --- y) x, | y , x ( G y) x, | y , x ( G21 ′ ′ = 12 ′ ′ (12) ---y) Y(µ x) X(β ) N(µ ) N(β ) y Y(µ ) x X(β m) S(n, m) (n, D L υ L L 1 y) x, | y , x ( G m n m n m n 1 n m 1 22 z m n, y x 22 ⋅ ⋅ ⋅ ′ ⋅ ′ ⋅ ⋅ ⋅ = ′ ′
∑ ∑
∞ = ∞ = avendo posto(
n,m z)
(
n,m z)
z m n, 11(n,m) υ L cosh υ L Bi(5)sinh υ L D = + (13)(
n,m z)
(
n,m z)
z m n, 22(n,
m)
υ
L
sinh
υ
L
Bi(0)cosh
υ
L
D
=
+
.Si osservi che, come già accennato in precedenza, la prima delle (11) risulta essere un’equazione integrale lineare del tipo di Fredholm di seconda specie [4] con la temperatura T(x,y,0) nel ruolo di funzione incognita e la funzione di Green G11 in quello di nucleo. Comunque è immediato riconoscere che, anche nel caso fosse Bi(0)=0, la natura integrale dell’equazione non scomparirebbe, anzi entrambe le (11). hanno tale natura dal momento che negli integrali dei loro secondi membri risultano incognite le funzioni
qˆ
(x,
y)
eTˆ
(x,
y)
.Adottiamo un indice numerico per indicare il generico elemento prismatico della pila, da 1 per quello di sommità fino ad n per quello di base; l’indice comparirà a pedice delle varie grandezze oppure tra parentesi, come apice. Con queste notazioni sulle interfacce del generico “iesimo” elemento la conservazione del flusso di calore e la continuità della temperatura si traducono nelle relazioni
) L y, (x, q y) (x, * P y) (x, q : y) (x, q (i-1) z 1 -i 1 -i 1 -i = + = ˆ ˆ per z=0 y,0) (x, T y) (x, T : y) (x, Tˆ = ˆi+1 = i+1 per z=L(i)z (14)
In questo modo per un generico elemento prismatico disponiamo di una coppia di equazioni integrali lineari nelle seguenti quattro funzioni
y) x, ( Tˆ ; y) x, ( Tˆ ; y) x, ( qˆ ; y) x, (
qˆi-1 i i i+1 e da ciò discende un sistema di equazioni integrali lineari che risultano in numero pari al numero delle funzioni incognite.
Se indichiamo con n il numero degli strati della struttura, si potrebbe frettolosamente concludere che 2n sono il numero di coppie di equazioni e altrettante sono le coppie di
funzioni flusso e temperatura. In realtà ad un conteggio più attento il numero di equazioni e di funzioni incognite risulta pari a 2(n-1). Infatti, poiché il parallelepipedo collocato alla sommità della pila non sostiene alcun’altro elemento, la sua faccia superiore è priva della parte A~ su cui sono da calcolare gli integrali della temperatura T(x,y,0); ne segue che la suddetta temperatura scompare dal secondo membro della coppia di equazioni relative al primo elemento e ciò esclude dal sistema, come inessenziali, sia la funzione stessa che l’equazione ad essa corrispondente. Anche per il flusso termico che attraversa la faccia inferiore dell’elemento posto alla base della pila si giunge alla medesima conclusione, dal momento che è immediato riconoscere che tale flusso non compare al secondo membro della coppia di equazioni di nessun altro elemento. Grazie a queste osservazioni diminuisce di due unità sia il numero di funzioni che di equazioni.
Infine si deve osservare che, se per il parallelepipedo collocato alla sommità della pila il flusso qˆ(x, y) è ovviamente nullo, per l’elemento posto alla base della pila la funzione
y) (x,
Tˆ all’interfaccia inferiore è la temperatura stessa del pozzo termico sul quale poggia la pila medesima, ovvero una funzione F(x,y) assegnata.
Sulla base di quanto abbiamo detto, il sistema di equazioni integrali lineari risulta:
[
]
∫∫
∫∫
′ ′ ′ ′ ′ ′ + ′ ′ − + ′ ′ ′ ′ ′ ′ + = A(1) (1) 22 2 1 1 (1) z 1 A(1) (1) 21 1 1 1 y d x y)d x, | y , x ( G ) y , x ( Tˆ ) y , x ( P R L k y d x y)d x, | y , x ( G ) y , x ( P y) (x, P y) (x, qˆ * * * (15a) ---[
]
[
]
∫∫
∫∫
∫∫
′ ′ ′ ′ ′ ′ + ′ ′ + + ′ ′ ′ ′ ⋅ ′ ′ + ′ ′ + + ′ ′ ′ ′ ′ ′ = + A(i) (i) 12 1 i i i (i) 11 A(i) 1 -i i i (i) z i (j) 11 1) -A(i i i i y d x y)d x, | y , x ( G ) y , x ( Tˆ ) y , x ( P R y d x y)d x, | y , x ( G ) y , x ( qˆ ) y , x ( P k L y d x y)d x, | y , x ( G ) y , x ( Tˆ (0) Bi y) (x, Tˆ * * (15b) ---[
]
[
]
∫∫
∫∫
∫∫
′ ′ ′ ′ ′ ′ + ′ ′ − + ′ ′ ′ ′ ′ ′ + ′ ′ + ′ ′ ′ ′ ′ ′ + = + A(i) (i) 22 1 i i i (i) z i (i) 21 A(i) 1 -i i (i) 21 1) -A(i i (i) 0 i i y d x y)d x, | y , x ( G ) y , x ( Tˆ ) y , x ( P R L k y d x y)d x, | y , x ( G ) y , x ( qˆ ) y , x ( P y d x y)d x, | y , x ( G ) y , x ( Tˆ h y) (x, P y) (x, qˆ * * * (15c) --- ---[
]
[
]
∫∫
∫∫
∫∫
′ ′ ′ ′ ′ ′ + ′ ′ + + ′ ′ ′ ′ ⋅ ′ ′ + ′ ′ + + ′ ′ ′ ′ ′ ′ = A(n) (n) 12 n n (n) 11 A(n) 1 -n n n (n) z (n) 11 1) -A(n n n n y d x y)d x, | y , x ( G ) y , x F( ) y , x ( P R y d x y)d x, | y , x ( G ) y , x ( qˆ ) y , x ( P k L y d x y)d x, | y , x ( G ) y , x ( Tˆ (0) Bi y) (x, Tˆ * * (15d)dove si deve tenere presente che ogni equazione si riferisce ad una base di un elemento e che nelle equazioni relative ad elementi diversi le coordinate x,y non sono in genere identiche, essendo riferite a sistemi con assi tutti paralleli, ma con origini non necessariamente coincidenti.
In linea di principio, la soluzione del sistema fornisce le funzioni flusso e temperatura alle interfacce; dalla loro conoscenza si hanno le funzioni f(x,y) e g(x,y) per ogni elemento prismatico, e ciò rende utilizzabile la soluzione del problema conduttivo con condizioni convettive al contorno e quindi calcolabile, elemento per elemento, il campo termico in tutta la struttura.
Dal momento che non è pensabile di risolvere in modo analitico il sistema di equazioni integrali, si rende necessaria una soluzione approssimata. Mediante il ricorso al calcolo numerico degli integrali il sistema integrale può essere trasformato in un sistema algebrico lineare e risolto con l’aiuto dei consueti strumenti di calcolo elettronico.
1.3 FORMULAZIONE ALGEBRICA
Una singola equazione lineare integrale di Fredholm, dal momento che è formulata su un intervallo finito, può essere ridotta ad un sistema di equazioni algebriche richiedendo che sia verificata in un numero finito di punti e quadrando, in modo approssimato, l’integrale definito mediante i valori assunti nei medesimi punti dalla funzione incognita [4]. Questo metodo è estensibile direttamente ai sistemi di equazioni integrali lineari ed in particolare è applicabile al sistema (15) di cui fornisce una soluzione approssimata. Come primo passo si noti che gli integrali che compaiono nell’equazioni del sistema sono tutti del medesimo tipo e per una generica funzione Φ possono essere così espressi
⋅ = ′ ′ ′ ′ ⋅ ′ ′
∑∑
∫∫
∞= ∞= 1 n m 1 m n j i A j i(x,y |x,y)dxdy C (n,m)X(β x)Y(µ y) G ) y , x Φ(y
d
x
)d
y
)Y(µ
x
X(β
)
y
,
x
Φ(
L
L
1
m n Lx 0 Ly 0 y x′
′
′
′
′
′
⋅
∫ ∫
(16)Scelto il tipo di tecnica di quadratura approssimata in due dimensioni, ed identificato sul dominio A un opportuno reticolo di N punti in cui calcolare la funzione Φ, si ha
) y , Φ(x ) y , (x B y d x )d y )Y(µ x X(β ) y , x Φ( L L 1 k k N 1 k k k m n, m n LxLy y x ⋅ ≅ ′ ′ ′ ′ ′ ′
∑
∫ ∫
= 0 0 (17) dove i coefficienti Bn,m dipendono dal tipo di quadratura adottata, oltre che dai valori assunti nei punti del reticolo dalle primitive delle autofunzioni.Ad esempio, nella tecnica di quadratura parallelepipeda su di un rettangolo di lati 2a e 2b si approssima la funzione Φ col valore assunto da essa nel punto di intersezione delle diagonali ottenendo )] y sin( µ L µ Bi(3) ) y [cos( µ )] x sin( β L β Bi(1) ) x b)[cos( β a)sin( µ sen( β 4 ) y , (x B k m y m k m k n x n k n m n k k m n, + ⋅ + + ⋅ = (18)
In ogni caso ponendo
∑∑
∞ = ∞ = ⋅ ⋅ = 1 n m 1 m n k k m n, ij k k ij(x ,y |x,y) C (n,m) B (x ,y ) X(β x)Y(µ y) φ (19)∑
∫∫
′
′
⋅
′
′
′
′
≅
N= 1 k k k k k ij A ij(
x
,
y
|
x,
y)d
x
d
y
φ
(x
,
y
|
x,
y)
Φ(x
,
y
)
G
)
y
,
x
Φ(
(20)Per introdurre questa approssimazione nel sistema di equazioni integrali (15) dobbiamo fare una importante precisazione: ogni elemento della pila ha un proprio unico sistema di coordinate a cui sono riferiti i punti delle facce z=0 e z=Lz(i), ma sulle due facce,
geometricamente identiche, i reticoli individuati per le quadrature sono in genere diversi per dimensioni della maglia e numero di punti, (vedi fig. 1.3.1). È invece necessario che, sulle interfacce di contatto, due elementi contigui abbiano reticoli identici, perfettamente sovrapponibili.
Naturalmente le coordinate di un punto pensato come appartenente alla superficie dell’elemento superiore ha in generale coordinate diverse da quelle del medesimo punto, pensato sulla superficie dell’elemento sottostante.
In conformità a quanto abbiamo detto, poiché ogni equazione del sistema (15) vale per tutti punti della faccia a cui l’equazione è riferita, tanto più deve essere verificata per i soli punti del reticolo adoperato per la quadratura, dando origine ad un pari numero di equazioni algebriche; l’insieme di tutte le equazioni algebriche originate dall’insieme delle equazioni integrali costituisce il sistema algebrico lineare a cui è ricondotto il sistema integrale.
Le notazioni x(i), y(i) si riferiscono alle coordinate di un generico elemento della pila per mettere in evidenza che in genere non sono identiche; xt(i), yt(i) per i punti appartenenti
alla faccia superiore z=0 dell’elemento iesimo; xb(i), yb(i) per i punti appartenenti alla
faccia inferiore z=Lz(i) dell’elemento iesimo. Inoltre, per evidenziare che le sommatorie
si riferiscono a reticoli di integrazione generalmente diversi, sono stati usati i simboli k e p per gli N(i) e M(i) punti dei reticoli tracciati, rispettivamente, sulle facce z=0 e z=Lz(i) dell’elemento iesimo, mentre il simbolo j è stato impiegato per l’interfaccia à di
contatto tra due elementi contigui: si tratta di M(i-1) punti dal momento che, sui complessivi N(i) punti del reticolo tracciato sulla faccia z=0 dell’elemento iesimo, l’intero reticolo della faccia z=Lz(i-1) dell’elemento sovrastante si sovrappone in genere
solo in parte, ma esattamente per tutti i suoi M(i-1) punti. Le notazioni sono riassunte in fig. 1.5.
Facendo uso delle notazioni suddette ed utilizzando le Eq. (19) e (20) per la conversione degli integrali doppi, il sistema di Eq.(15) viene trasformato in un sistema algebrico formato da 2[M(1)+M(2)+....+M(n-1)] equazioni in altrettante incognite.
La sua forma normale, scritta in modo conciso ed in cui si sono isolate a sinistra le variabili incognite, è la seguente:
(1) p 1 M(1) 1 p (1) pb N(1) 1 k (1) k (1) kb (1) b (1) b (2) p M(1) 1 p (1) pb T q P* φ P ω R* P* ω ⋅ + = +
∑
⋅ −∑
⋅ ⋅∑
= = = (21) con b =1,2,3...M(1) --- ---∑
∑
∑
∑
∑
= = = = + = ⋅ + ⋅ = = ⋅ − ⋅ + ⋅ − M(i) 1 p (i) p i (i) t p N(i) 1 k (i) k (i) k t 1) -M(i 1 j 1) -(i j (i) t j M(i) 1 p 1) (i p (i) t p 1) -M(i 1 j (i) j (i) t j ) i ( 0 (i) t * *P R φ P ψ q ψ T φ T ψ h Tcon t =1,2,3...M(i-1) ≤ N(i)
---
FIG 1.3.1 Schema degli indici degli strati, delle coordinate e dei reticoli utilizzati nella trattazione numerica.
∑
∑
∑
∑
∑
= = = + = = ⋅ − ⋅ + = = + ⋅ − ⋅ + ⋅ − M(i) 1 p (i) p i (i) b p N(i) 1 k (i) k (i) b k (i) b (i) b 1) -M(i 1 j 1) -(i j (i) b j 1) (i p M(i) 1 p (i) b p (i) j 1) -M(i 1 j (i) b j ) i ( 0 * * * φ P ω R P P q q φ T ω T φ h con b =1,2,3...M(i) --- ---[
p]
(n) p n M(n) 1 p (n) t p N(n) 1 k (n) k (n) k t 1) -M(n 1 j 1) -(n j (n) t j 1) -M(n 1 j (n) j (n) t j ) n ( 0 (n) tF
P
R
φ
P
ψ
q
ψ
T
ψ
h
T
* *+
⋅
+
⋅
=
=
⋅
−
⋅
−
∑
∑
∑
∑
= = = = con t =1,2,3...M(n-1) ≤ N(n) (21) ---dove si è indicato con
)
y
,
(x
T
T
(i) k (i) k i (i) k≡
ˆ
;q
q
(x
,
y
(i)k)
(i) k i (i)k
≡
ˆ
; Pk(i) ≡Pi(x(i)k ,y(i)k )) y , (x P P (i) p (i) p i (i) p* ≡ * ; ) y , (x P P (i) p (i) p i (i) p* ≡ * ;
)
y
,
F(x
F
p≡
p p (22) e con)
y
,
x
|
y
,
(x
φ
k
L
ψ
(i) t (i) t (i) k (i) k (i) 11 i (i) z (i) k t≡
)
y
,
x
|
y
,
(x
φ
)
y
,
x
|
y
,
(x
φ
φ
(i) t (i) t (i) p (i) p (i) 21 (i) t (i) t (i) p (i) p (i) 12 (i) t p≡
=
)
y
,
x
|
y
,
(x
φ
)
y
,
x
|
y
,
(x
φ
φ
(i) b (i) b (i) k (i) k (i) 12 (i) b (i) b (i) k (i) k (i) 21 (i) kb≡
=
)
y
,
x
|
y
,
(x
φ
L
k
ω
(i) b (i) b (i) p (i) p (i) 22 (i) z i (i) pb≡
(23)Le quantità definite dalle (23) costituiscono i coefficienti dei singoli aggiunti rettangolari della matrice principale del sistema algebrico, organizzata come in fig. 1.3.2. La risoluzione del sistema consente la conoscenza delle griglie di valori di flusso e temperatura su tutte le interfacce interne della struttura. Con questi dati è possibile infine calcolare il flusso e la temperatura in ogni punto dell’assemblaggio ottenendo una mappatura tridimensionale completa.
FIG 1.3.2 Schema grafico del sistema algebrico (4 strati). I è la matrice identità, T.N. è il vettore colonna dei termini noti. Gli aggiunti in bianco sono matrici nulle
1.4 ESEMPI DI SIMULAZIONE
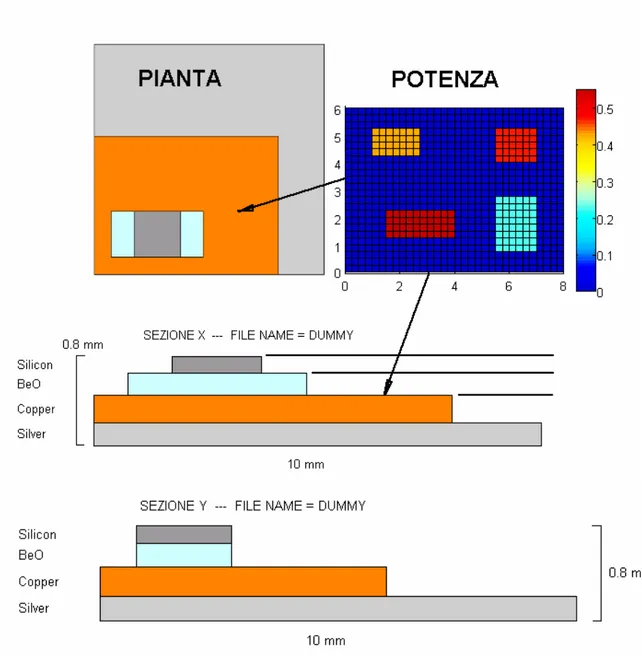
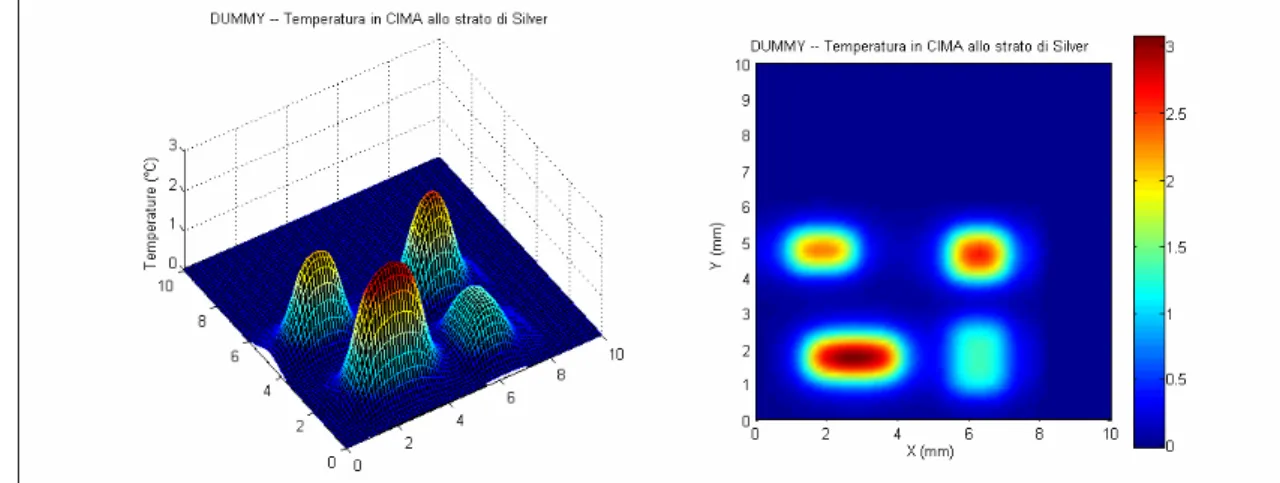
Prendiamo una semplice struttura piramidale e studiamola con DJOSER con tutte le informazioni che il programma riesce a fornirci.
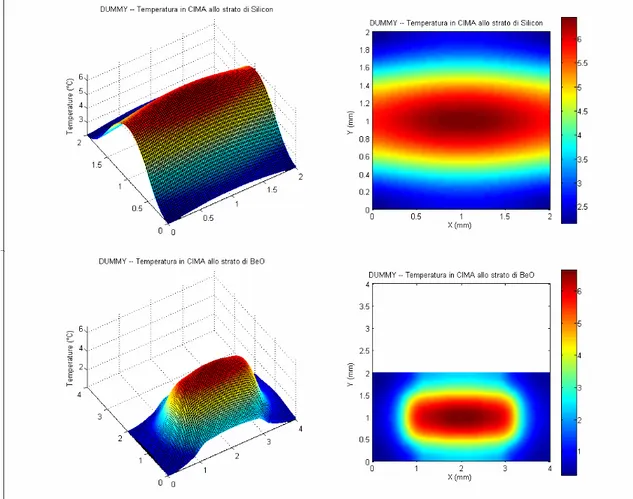
Questa struttura presenta asimmetria e distribuzione di potenza a cluster. Inoltre gli ultimi due strati sono altamente conduttivi: prevediamo pertanto che le linee di flusso, più strette nei primi due strati poco conduttivi, si allarghino nel passaggio negli ultimi sue strati. Inoltre abbiamo imposto resistenze termiche di contatto nulle fra gli strati: condizione questa idealizzata, ovviamente. Vediamo intanto le mappe termiche forniteci da DJOSER
Vediamo infine i profili di temperatura degli altri due strati, quello di rame e quello di argento.
CAPITOLO II
PROVE SULLA ACCURATEZZA
DELLA SIMULAZIONE
ANALITICA
2.1.
Confronto con simulazione FEM
………..….pag. 35
2.1. SIMULAZIONE DJOSER
Dopo aver illustrato i presupposti teorici sui cui si basa DJOSER [3], passiamo a confrontare le sue prestazioni rispetto ad un software basato sull’implementazione ad elementi finiti. E’ stato utilizzato il programma MARC ed il pre-post-processore MENTAT. Le simulazioni FEM sono state effettuate utilizzando una griglia molto più fitta del necessario (circa 6400 nodi) al fine di ridurre al minimo l’errore nel calcolo dei flussi e della temperatura rispetto alla realtà. In pratica è risultata una suddivisione in elementi cubici di dimensioni laterali di 0.1 mm, ovvero la metà di quelli bidimensionali impostati per lo DJOSER.
Le strutture prese in esame sono strutture virtuali fatte analizzare da DJOSER e da MARC. Esse sono delle strutture piramidali multistrato.
STRATO (W/m°C)k (mm) Lx (mm) Ly (micron)Lz
Silicio 135 6.2 4.4 500 Argento 419 9 7 200
Allumina 24 14 10 500
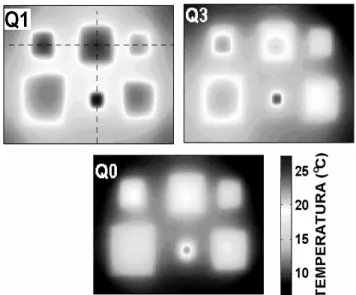
I campioni virtuali utilizzati per le simulazioni sono i seguenti. Il campione Q0, composto da quattro strati, costituisce la struttura base assialsimmetrica; ha le superfici
in contatto con l’ambiente adiabatiche e la potenza dissipata è localizzata in cima allo strato di silicio. La scelta di alternare materiali a bassa e alta conduttività termica è stata fatta per testare l’effetto sul flusso termico delle differenti conducibilità. Il primo strato è di silicio; la generazione di calore (potenza totale di 17.4 W) è localizzata sulla faccia superiore ed è organizzata in isole quadrate, ognuna avente la sua densità di potenza uniforme. L’intera superficie di silicio è suddivisa in griglie di 31x22 celle quadrate di 0.2mm per lato.
Gli atri strati sono costituiti da un film sottile e conduttivo di argento, uno strato isolante di allumina e uno strato più esteso di rame che allarga il flusso termico. Su tutte le facce superiori e laterali sono state considerate adiabatiche tranne la base supposta in contatto con un pozzo termico ideale la cui temperatura è settata costante a 0 °C.
Le varianti Q1 e Q3 differiscono da Q0 per un solo dettaglio strutturale (doppio spessore di allumina per Q1 ed una totale asimmetria degli strati per Q3). Questi campioni sono stati utilizzati per un confronto diretto con Q0, in modo da osservare gli effetti sulla distribuzione di temperatura dello strato superiore dovuta a variazioni delle
FIG 2.1.1 Mappe termiche e mappe di flusso sulle interfacce delle superfici costituenti Q0 .
comportamento termico della struttura Q0 è stato inoltre calcolato imponendo uno scambio termico convettivo su tutte le pareti verso l’ambiente circostante, ad eccezione della base in contatto con un termostato, utilizzando vari valori del coefficiente di scambio termico, dal caso di aria ferma fino a valori molto elevati. La fig. 2.1.2 mostra le mappe di temperatura fornite dal programma DJOSER nei tre casi presenti, nella cui rappresentazione è stata utilizzata la stessa scala di colori per rendere evidente il confronto.
E’ possibile notare subito l’influenza nella distribuzione della temperatura della variazione di spessore degli strati (fra Q0 e Q1) e della asimmetria (fra Q0 e Q3). Le distribuzioni di temperatura delle tre strutture differiscono notevolmente, nonostante esse siano state simulate a parità di potenza fornita. Tali differenze sono perfettamente consistenti con le diverse configurazioni geometriche e gli strati sotto il chip di silicio, i quali si comportano da vie di fuga per il calore generato sulla superficie superiore.
Il campione Q1 mostra una distribuzione di temperatura che è molto simile a quella di Q0, ma aumentata di un fattore costante, a causa del maggiore spessore di allumina, che è il materiale termicamente più isolante dell’intera pila. Le distribuzioni per Q3 mostrano non soltanto un aumento nella distribuzione di temperatura rispetto a Q0, ma
FIG 2.1.2 Mappe termiche della superficie del silicio per i campioni Q0, Q1 E Q3 in condizioni adiabatiche
anche una deformazione, che è particolarmente evidente nell’angolo in basso a sinistra della mappa. La differente distribuzione del flusso termico negli strati interni, dovuta alla forte asimmetria della struttura è la causa di tale effetto. Il posizionamento dell’area dissipante sull’angolo della lastra impedisce infatti la diffusione laterale del flusso termico, la cui concentrazione in una zona ristretta comporta un innalzamento locale della temperatura superficiale.
In fig. 2.1.3 è riportato anche l’andamento della temperatura lungo le direttrici segnate 2.1.2. Da queste rappresentazioni appare evidente come la geometria e la simmetria della struttura siano influenti nella distribuzione del flusso termico.
Nella fig. 2.1.4 sono illustrati gli andamenti di temperatura della superficie del silicio in Q0 lungo le due consuete sezioni verticale ed orizzontale, calcolati nella condizione adiabatica (hv=0) e per altri casi in cui sono imposti vari valori del fattore di scambio termico convettivo di tutte le superfici a contatto con l’ambiente nel range 8 – 20000 W/ºC m2, ovvero da una condizione di aria ferma ad una irrealistica di fortissima
FIG 2.1.3 Andamenti delle temperature lungo le sezioni di fig. 1.7 per i campioni Q0, Q1 e Q3 in condizioni adiabatiche ad eccezione della base
Ta è stata fissata a –10 ºC mentre quella del termostato sottostante T0 è 0 ºC . In effetti nei grafici di fig. 2.1.3 sono stati rappresentati soltanto gli andamenti per hv = 1000, 5000, 10000 e 20000 W/ºC m2 in quanto le temperature ottenute per valori inferiori di hv si discostano dal caso adiabatico in modo trascurabile (meno di mezzo grado centigrado) e non sono quindi rappresentabili su quella scala. Questo almeno nei casi in cui le resistenze termiche di contatto fra gli strati e fra l’intera struttura ed il pozzo termico non presentino valori eccessivi.
FIG 2.1.3 Andamenti delle temperature lungo le sezioni di fig. 2.1.1 per il campione Q1 e per vari valori del coefficiente di scambio convettivo verso l’ambiente
2.2. DISCUSSIONE SULL’ACCURATEZZA
La valutazione dell’errore sulla superficie superiore della piramide deve tener conto di due fattori:
1. l’approssimazione per troncamento delle infinite serie armoniche che compaiono all’interno del sistema integrale (eqq. 16, 17, 19 par. 1.3 );
2. l’approssimazione dovuta alle formule di quadratura delle funzioni di flusso e temperatura, necessarie per la valutazione degli integrali.
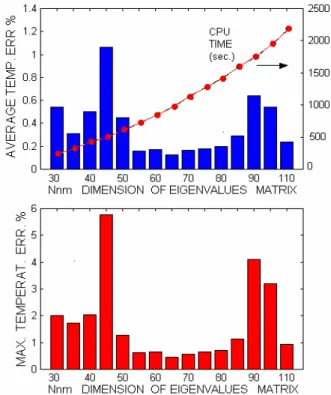
Per quanto riguarda la prima causa di errore, l’eq. (19) del par. 1.3 rappresenta una doppia serie armonica infinita, definita da vettori bidimensionali illimitati di autovalori βn e µm. Tali serie sono lentamente convergenti e la funzione errore di troncamento ha generalmente un andamento decrescente ma anche irregolarmente oscillante. Nel presente caso tali serie sono state calcolate utilizzando un numero intero massimo Nnm per gli indici n e m. Questo valore deve essere impostato separatamente per ogni strato della struttura. Per evidenziare il tipico errore indotto da questo fattore, la percentuale d’errore di temperatura è calcolato per un ampio range di Nnm in una struttura semplificata composta solamente dallo strato di silicio del campione di prova Q0, con la stessa potenza applicata, con le medesime densità, e dove tutti gli altri strati della pila sono stati rimpiazzati da un coefficiente convettivo uniforme, di valore opportuno, sulla faccia inferiore dello strato di silicio (fig. 2.2.1.)
FIG 2.2.1 Struttura semplificata per verificare l’effetto del numero di autovalori sull’errore complessivo
Questo modello è chiaramente differente rispetto a Q0, molto più veloce da analizzare, con una perdita di accuratezza sui risultati a causa della perdita di informazioni dovute alla dislocazione interna del flusso termico che si mantiene intorno al 6%. Tuttavia esso ci permette di valutare velocemente l’errore per un singolo strato in un singolo punto della superficie di silicio, con un numero molto elevato di autovalori.
La fig. 2.2.2 mostra i grafici dell’errore percentuale in funzione di Nnm in due singoli punti della superficie: il centro (curva A) ed il bordo (curva B) dell’isola di dissipazione ad area minore, proprio dove si raggiunge il massimo della temperatura.
Nel caso di una struttura multistrato l’errore totale compiuto nella valutazione della temperatura è dovuto alla somma degli errori di troncamento delle serie armoniche su ogni singolo strato. Per studiare gli effetti cumulativi dell’errore di troncamento è chiaramente più agevole studiare una struttura come quella mostrata in fig. 2.2.1 nella quale il numero di interfacce è ridotto. Ne ricaviamo così un grafico in funzione di Nnm, come riportato in fig. 2.2.3. Nella figura è inoltre mostrato il tempo in secondi necessario all’analisi termica.
Come si può notare l’altezza delle non è monotonamente decrescente all’aumentare di Nnm, come ci si potrebbe aspettare, ma sono presenti dei picchi più alti causati dalla natura oscillatoria e irregolare dell’errore di troncamento. Essi, probabilmente, corrispondono ai casi in cui gli errori nei vari strati hanno lo stesso segno, e quindi tendono algebricamente a cumularsi.
FIG 2.2.2 Andamenti dell’errore percentuale in funzione del numero di autovalori dello strato di silicio, al centro (A) ed al bordo (B) dell’isola di dissipazione più piccola.
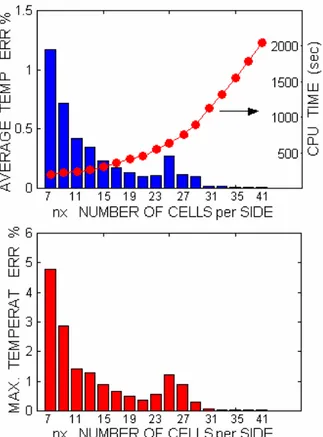
La seconda causa di errore nella valutazione della distribuzione di temperatura nella densità delle griglie per la descrizione delle funzioni continue bidimensionali di flusso e temperatura per mezzo di funzioni costanti a tratti.
L’uso di una griglia di celle non uniforme, più densa dove si manifestano maggiori variazioni di temperatura, può essere effettivamente utile al fine di controllare tale errore, ma in tal maniera l’operazione di costruzione del modello diverrebbe più complessa e quindi una delle caratteristiche di semplicità del programma DJOSER andrebbe perduta. D’altra parte un aumento del numero di celle in corrispondenza delle interfacce comporterebbe un aumento del tempo di calcolo. L’effetto di questo secondo tipo di errore può essere osservato in fig. 2.2.4 dove è mostrato l’errore relativo percentuale medio (diagramma in alto) e massimo (diagramma in basso) calcolati su tutta la superficie del silicio. Il numero di celle per lato sulle facce inferiori dei due strati è stato variato nel range 5-43, mantenendo costante la densità delle celle sulla faccia superiore dello strato di silicio.
FIG 2.2.3 Errore medio (sopra) e massimo (sotto) in funzione del numero di celle Nnm
Tali grafici mostrano un comportamento decrescente abbastanza regolare all’aumentare del numero di celle, a parte un piccolo picco all’interno dell’intervallo 20-30, probabilmente dovuto ad un fenomeno di risonanza col valore del numero di autovalori utilizzato. I tempi di calcolo impiegato dal simulatore riportati nei grafici di figg. 2.2.3 e 2.2.4 sono stati valutati utilizzando un processore Pentium 4 (1.5 GHz). Il programma DJOSER è stato per ora utilizzato in forma interpretata in ambiente MATLAB, anziché compilata; per questa ragione il tempo di calcolo non è direttamente confrontabile con quello del programma FEM. L’implementazione in formato eseguibile compilato del simulatore dovrebbe garantire una consistente diminuzione dei tempi di calcolo. Inoltre buona parte del tempo macchina (circa il 90%) è impiegato per la costruzione della matrice di coefficienti del sistema di equazioni lineari, la quale non dipende dalle condizioni al contorno. La matrice di tale sistema potrebbe essere memorizzata e utilizzata per altre simulazioni con differenti condizioni al contorno risparmiando il
FIG 2.2.4 Errore medio (sopra) e massimo (sotto) in funzione del numero di celle Nnm
relativo tempo di calcolo. Prevedendo un aumento medio della velocità dovuta alla compilazione della routine, il tempo di lavoro del programma DJOSER dovrebbe rimanere entro il 10% di quello necessario agli analoghi strumenti di calcolo FEM. Dopo questa analisi dell’effetto degli autovalori sulla accuratezza dell’analisi termica di DJOSER, vediamo il confronto con il metodo FEM sui campioni Q0, Q1 e Q3. Le analisi sono state effettuate da DJOSER e da FEM sulle medesime linee ortogonali tracciate in fig. 2.1.2, con i risultati mostrati in fig. 2.2.5.
Vediamo che a fronte d’un risparmio nel tempo di computazione del 10% l’errore commesso rimane al di sotto dell’1%.
FIG 2.2.5 Percentuale di errore relativo di DJOSER rispetto a FEM lungo i due piani traversi ortogonali
CAPITOLO III
VALIDAZIONE SPERIMENTALE I
3.1.
Costruzione dei campioni
………..……….pag. 48
3.2.
Misurazione
…...………...pag. 54
3.3.
AVA
…..………pag. 58
3.4.
AAVRA
………pag. 71
3.1. COSTRUZIONE DEI CAMPIONI
Per la validazione sperimentale sono stati tre coppie di campioni, tre strutture monodimensionali e tre strutture “piramidali”. Il motivo per il quale di ogni tipo di modello ne sono state fatte due strutture differenti risiede nel meccanismo di conduzione. La struttura monodimensionale permette una dispersione di flusso termico limitata, e le linee di flusso termico sono pressoché normali ai parallelepipedi che la costituiscono.
Oltre a ciò la struttura monodimensionale non prevede trasporto di calore per convezione naturale sulle pareti orizzontali dei prismi paralleli che lo costituiscono, nonostante sia essa generalmente trascurabile rispetto alla conduzione. Nella struttura monodimensionale dunque assumiamo il flusso termico monodimensionale, con direzione quella normale alle superfici. Per converso nella struttura “a piramide” il flusso termico, in ogni sezione longitudinale, si disperde come rappresentato in fig. 31.1.
Sulla sommità delle strutture sono state incollate tramite una colla termica specifica (xxxxxxxx) delle resistenze a film spesso depositate su un substrato di allumina. Sono inoltre stati presi materiali con differenti, conduttori (rame, alluminio) e isolanti (vetro, mica) e sono stati incollati per creare i sei modelli in oggetto.
L’assetto termico dello strato sulla sommità e la sua temperatura massima sono fortemente influenzati dal valore delle resistenze termiche di contatto alle interfacce, ovvero allo strato di colla ed in ultimo del grasso termico (yyyyyyyy) con cui abbiamo
riscaldatori
linee di flusso termico
convezione
FIG 3.1.1 Esemplificazione delle differenti modalità di trasmissione del calore nella struttura monodimensionale e in quella “a piramide”
incogniti poiché dipendono dai parametri tecnologici di deposizione e dalle condizioni di rugosità delle superfici di contatto (fig. 3.1.2). Così attraverso i campioni monodimensionale, che permettono una distribuzione di flusso termico pressoché uniforme, possiamo calcolare la resistenza termica specifica infatti possibile calcolare la resistenza termica di contatto come prodotto tra la resistenza termica specifica dello strato e l’area. Prima abbiamo caratterizzato i materiali di cui non conoscevamo le
conducibilità termiche, essenzialmente di colla termica e grasso termico. Noti questi valori abbiamo potuto proseguire nella nostra analisi inserendo la resistenza di contatto relativa all’interfaccia come parametri per lo DJOSER.
Per le misurazioni della temperatura abbiamo utilizzato un sensore termico a singola resistenza al platino con la seguente caratteristica:
00385 . 0 1 100 ) ( ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Ω − = ° R C T
Abbiamo dunque preso una struttura di prova costituita da una resistenza a film spesso depositata su un substrato di allumina di area (23x23 mm2) e di spessore di 1 mm.
FIG 3.1.2 Ingrandimento che mette in evidenza come possibili rugosità od asperità delle superfici, e non uniformità dello strato di colla possano influire fortemente
la distribuzione del flusso termico, facendo così variare la temperatura sulla sommità della struttura.
FIG 3.1.3 Immagine della struttura di prova costituita dalla sola lastra di allumina con sopra la resistenza a film spesso..
Abbiamo pertanto posto la struttura sul piatto di un termostato posto a 20°C all’interno d’una campana per il vuoto, contattando la struttura al piatto con un sottile film di grasso. Abbiamo applicato alla resistenza delle potenze variabili e ne abbiamo misurato la temperatura sulla sommità attraverso il sensore RTD al platino.
I risultati sono stati i seguenti.
I(A) V(A) P(W) R(Ohm) T(°C)
0,2 1,873 0,375 111,2 29,091 0,5 4,688 2,344 111,5 29,870 0,7 6,564 4,595 112 31,169 1 9,383 9,383 112,9 33,506 1,2 11,264 13,517 113,7 35,584 1,4 13,14 18,396 114,8 38,442 1,5 14,09 21,135 115,3 39,740 Rg+Ra=0.5191 °C/W
In situazioni di flusso termico uniforme posso considerare
) ( ) ( W P C T Rth = °
Dunque interpolando con MATLAB i dati ottenuti, riportati su un grafico che sulle ascisse mappa la T(°C) e sulle ordinate P(W), sperimentalmente otteniamo
Con un coefficiente angolare, e dunque una resistenza termica complessiva, di
2 3 0.591 /
grasso Al O
R +R = °C W
DJOSER dà, per questa struttura, le seguenti mappe termiche e i dati sotto riportati (fig. 3.1.6 e fig. 3.1.7). 0 5 10 15 20 25 28 30 32 34 36 38 40 °C POTENZA (W)
SEZIONE X -- FILE NAME = A ---- Po = 1 W Al2O3 Al2O3 23 mm 1 mm Sottraendo al valore 2 3 0.591 / grasso Al O
R +R = °C W normalizzato per unità di area, ovvero diviso per (23x23mm2), il valore Rthdell’allumina, noto, troviamo per sottrazione un valore indicativo di quella del grasso (yyyyyyyy)
0.1542 /
grasso
R = °C W
Ovvero riportato sulla superficie 2
81,56 /
grasso
R = mm C W°
FIG 3.1.6 Sezione e pianta della struttura in allumina in oggetto, con le relative misure espresse in [m-3]: l’area in rosso identifica l’area attiva, la resistenza a film spesso
FIG 3.1.7 Mappa termica fornita da DJOSER della struttura -10 -5 0 5 10 -10 -5 0 5 10 FILE NAME = A ---- Po = 1 W Lx (mm) Ly ( m m ) mm mm mm mm mm mm °C
Dobbiamo precisare che questo valore è un valore indicativo, in quanto dipende dall’uniformità della distribuzione del grasso termico. In altre parole, essendo esso stato spalmato manualmente e non con processi automatizzati, è un valore indicativo affetto da variabili aleatorie come spessore e pressione con cui il dispositivo è premuto sul termostato.
Con prove analoghe abbiamo determinato, come vedremo, anche la resistenze termiche
colla
3.2. MISURAZIONE
Con i nomi di AVA, AAVRA e AMAMR abbiamo indicato le tre coppie “sigaro”-“piramide” costituite rispettivamente dei seguenti materiali:
• AVA da allumina, vetro, alluminio;
• AAVRA da allumina, alluminio, vetro, rame, alluminio; • AMAMR da allumina, mica, alluminio, mica, rame.
Di ognuno di questi campioni evidenzieremo le prove compiute con l’RTD al platino, lo DJOSER e con telecamera a raggi infrarossi AVIO Neo Thermo TVS-600 in grado di visualizzare, con opportuna scala cromatica, i salti termici riscontrati nella struttura, osservata in direzione normale alla sua superficie superiore. Le immagini termiche ottenute presentano anche i valori assoluti di temperatura in tre punti osservati, calcolati tenendo conto di un valore di emissività delle superfici misurato tramite taratura della telecamera a 0.97. A tale proposito tutte le strutture sono state annerite con nero fumo per ottenere valori di emissività il più possibile uniformi, indipendentemente dai vari tipi di materiale costituenti le strutture. Le riprese delle piramidi sono state compiute con due diversi gradi di risoluzione della telecamera. Si è utilizzata una lente da 35mm a più bassa risoluzione per le riprese a campo più largo per visualizzare l’intera struttura, e una lente da 70mm per visualizzare il campo di temperatura più stretto, limitato al solo strato superficiale dell’elemento di prova, al solo riscaldatore. Dato che le riprese sono state effettuate in ambiente chiuso in assenza di ventilazione, le simulazioni termiche dei campioni sono state condotte assumendo un valore di 8 W/°Cm2 per il coefficiente di scambio termico convettivo delle pareti verso l’ambiente circostante.
FIG 3.2.3 Dati forniti a DJOSER della struttura AVA monodimensionale (sopra) e a piramide (sotto)
FIG 3.2.3 Dati forniti a DJOSER della struttura AAVRA monodimensionale (sopra) e a piramide (sotto)
FIG 3.2.5 Dati forniti a DJOSER della struttura AMAMR monodimensionale (sopra) e a piramide (sotto)
SEZIONE X -- FILE NAME = AVANEW ---- Po = 1 W Al2O3 glass175 Aluminum 23 mm 7.5 mm 40 50 60 70 80 90 3.3. AVA
Prendiamo la prima coppia, la coppia AVA. Di questa non conoscevamo preliminarmente la Rvetroe Rcolla.
I dati sperimentali ci porgono i seguenti risultati di resistenza termica
E questa è la consueta interpolazione dei dati per ricavare il coefficiente angolare della retta interpolante
I(A) V(A) P(W) R(Ohm) T(°C)
0,2 3,456 0,691 110,8 28,052 0,3 5,18 1,554 111,5 29,870 0,4 6,904 2,762 112,4 32,208 0,5 8,628 4,314 113,5 35,065 0,6 10,35 6,210 115,2 39,481 0,7 12,07 8,449 117,4 45,195 0,8 13,78 11,024 120,2 52,468 0,9 15,49 13,941 123,4 60,779 1 17,2 17,200 127,1 70,390 1,1 18,91 20,801 131,2 81,039 Rg+Ra+Rv+Rc=2.8089 °C/W -10 -5 0 5 10 -10 -5 0 5 10
FILE NAME = AVANEW ---- Po = 1 W
Lx (mm)
Ly
(
mm)
FIG 3.3.1 Sezione e pianta del sigaro AVA con le relative misure espresse in [m-3]: l’area in rosso identifica l’area
attiva, la resistenza a film spesso
°C
mm
Nel confronto con DJOSER abbiamo considerato Rth media, poiché il vetro è molto
resistivo e quindi la T è massima al centro ma decresce rapidamente verso la periferia della struttura. Per come è sistemato il sensore inoltre non possiamo essere sicuri che la T rilevata sia "esattamente" la massima, ovvero che sia esattamente quella al centro del riscaldatore. Così, prendendo il valore che DJOSER fornisce come valore medio, ottengo 0.1542 / grasso R = °C W 2 3 1.8711 / Al O vetro Al grasso R +R +R +R = °C W sperimentalmente ho che: 2 3 2 2.8089 /
Al O vetro Al grasso colla
R +R +R +R + R = °C W
per differenza (solo per aver un'idea dell'ordine di grandezza, nata la non ortodossia del metodo)
0.4689 /
colla
R = °C W
resta da capire quale superficie è interessata dal flusso, ovvero se un’area pari a quella attiva (13.5mm x 18 mm) oppure a quella dell'intero dispositivo (23mm x 23mm). Dunque:
2
(0.4689 18 13.5) 113.9427⋅ ⋅ = <Rcolla(mm C W° / ) (0.4689 23 23) 248.0481< ⋅ ⋅ = con prove successive con DJOSER otteniamo un valore di
2
160 /
colla
R ≅ mm C W°
questo comporta un valore stimato da DJOSER di
2 3 2 2.5235 /
Al O vetro Al grasso colla
R +R +R +R + R = °C W
Questo dà un risultato con un margine del 10% circa di errore rispetto al valore sperimentale. Alcuni dati forniti da DJOSER per la struttura AVA:
FIG 3.3.2 Mappe di temperatura simulate da DJOSER, in ima allo strato di allumina (in alto) in cima allo strato di vetro (figura in mezzo) ed in cima allo strato di alluminio
mm mm mm mm mm mm mm mm mm mm mm mm °C °C °C
Oltre a ciò DJOSER fornisce i flussi di temperatura controllando che non vi siano flussi negativi, ovvero flussi di temperatura che si muovono dal basso verso l’alto. Se ciò avvenisse il troncamento della serie armonica operato da DJOSER sarebbe scorretto ed i risultati non attendibili. In sostanza è una sorta di riprova della bontà di quanto elaborato. I flussi sono rappresentati nelle figure fig. 3.3.4 e 3.3.5
FIG 3.3.4 Mappe dei flussi di temperatura simulate da DJOSER, in cima allo strato di allumina (figura in alto), in
cima allo strato di vetro (figura in basso)
mm mm
mm
SEZIONE X -- FILE NAME = AVANEW3D ---- Po = 1 W Al2O3 glass175 Aluminum 57.4 mm 8 mm
L’errore che DJOSER fornisce, come vedremo anche nelle prossime prove, non è strutturale, ovvero è legato ai difetti di costruzione e alla aleatorietà di alcuni fattori costruttivi come colla e grasso. Inoltre dipenderà dalla superficie interessata al flusso termico, ipotizzato uniforme, dal momento che questa va a moltiplicare la resistenza termica specifica. In altre parole nelle simulazioni con DJOSER verranno utilizzati valori di Rcolla e Rgrassoche saranno del solito ordine di grandezza, ma che differiranno
da coppia a coppia, tenendo conto che all’interno della coppia “sigaro”-“piramide” le caratteristiche costruttive e di flusso possono ragionevolmente considerarsi simili. Passiamo pertanto ad analizzare la “piramide” AVA. Come al solito diamo prima i risultati sperimentali che andranno a confermare i valori simulati da DJOSER.
FIG 3.3.5 Mappe dei flussi di temperatura simulate da DJOSER, in cima allo strato di alluminio
-30 -20 -10 0 10 20 30 -30 -20 -10 0 10 20 30
FILE NAME = AVANEW3D ---- Po = 1 W
Ly
(
m
m
)
FIG 3.3.6 Sezione trasversale lungo asse x e pianta della struttura AVA a “piramide”, con relative dimensioni
mm
mm
La RTD al platino ci porge i seguenti valori, opportunamente interpolati da MATLAB come di seguito mostrato
I(A) V(A) P(W) R(Ohm) T(°C)
0,2 3,759 0,752 111,4 29,610 0,3 5,635 1,691 112,2 31,688 0,4 7,512 3,005 113,5 35,065 0,5 9,387 4,694 115,2 39,481 0,6 11,258 6,755 117,4 45,195 0,7 13,13 9,191 119,9 51,688 0,8 14,99 11,992 122,8 59,221 0,9 16,86 15,174 126 67,532 Rg+Ra+Rv+Rc=2.6545 °C/W
Dalla consueta interpolazione otteniamo
2 3 2.6545 /
Al O colla vetro colla Al grasso
R +R +R +R +R +R = °C W
Vediamo i risultati offerti da DJOSER. Per la medesima struttura, coi valori di Rcollae grasso
R otteniamo:
2 3 2.4009 /
Al O colla vetro colla Al grasso
R +R +R +R +R +R = °C W
Un risultato prossimo, che verificheremo con il confronto con le misurazioni termografiche. Valutando ancora i risultati della simulazione con DJOSER vediamo delle interessanti rappresentazioni delle mappe di temperatura e dei flussi che il programma è in grado di fornirci.
0 2 4 6 8 10 12 14 16 25 30 35 40 45 50 55 60 65 70 °C POTENZA (W)
Queste le mappe di temperatura. Esse ci forniscono un’idea dell’effetto dello strato di vetro, isolante termico, sulla distribuzione del flusso di calore. Vediamo adesso le mappe di flusso.
FIG 3.3.7 Mappe di temperatura della struttura a piramide AVA, in cima allo strato di allumina (in alto), a quello del
vetro (centro) e a quello dell’alluminio (basso)
mm mm mm mm mm mm mm mm mm mm mm °C °C °C
FIG 3.3.8 Mappe di temperatura della struttura a piramide AVA, in cima allo strato di allumina (in alto), a quello del
vetro (centro) e a quello dell’alluminio (basso)
mm mm mm mm mm mm