Analisi sperimentale della sincronizzazione di reti di Chua con link dinamici

(1)

UNIVERSITÀ DEGLI STUDI DI NAPOLI FEDERICO II

FACOLTÀ DI INGEGNERIA

CORSO DI LAUREA IN INGEGNERIA ELETTRONICA

CLASSE DELLE LAUREE IN INGEGNERIA DELL’INFORMAZIONE, CLASSE n° 9

DIPARTIMENTO DI INGEGNERIA ELETTRICA

ELABORATO DI LAUREA

ANALISI SPERIMENTALE DELLA SINCRONIZZAZIONE DI RETI DI CHUA CON LINK DINAMICI

RELATORE

CH.MO PROF. MASSIMILIANO DE MAGISTRIS

CORRELATORE

ING. CARLO PETRARCA

CANDIDATO

PAOLO MARSILIA

Matr. 528/196

(2)

(3)

Dedicato alla mia splendida famiglia che tanto ha atteso questo momento.

(4)

RINGRAZIAMENTI

Desidero anzitutto ringraziare sentitamente il mio relatore Prof. Massimiliano De Magistris per l’opportunità che mi ha dato di contribuire allo sviluppo ed alla comprensione di questo affascinante argomento, per la sua grande professionalità e disponibilità a chiarirmi gli aspetti più ostici della materia, ma soprattutto per il suo sostegno morale e il suo incoraggiamento che, nei momenti più difficili, hanno saputo tirar fuori la parte migliore di me.

Desidero altresì ringraziare l’Ing Petrarca, mio correlatore, per la sua enorme pazienza nel seguire le fasi finali del lavoro e per i suoi preziosi suggerimenti.

Un ringraziamento particolare va infine alla mia famiglia che mi ha sempre spronato nei momenti di difficoltà ad arrivare a questo importante traguardo.

(5)

I

INDICE

INTRODUZIONE ... 1

Capitolo 1 ... 3

SINCRONIZZAZIONE DI RETI COMPLESSE... 3

1.1 Sistemi dinamici ... 3

1.1.1 Stabilità di un sistema dinamico ... 3

1.1.2 Esponenti di Lyapunov ... 6

1.2 Il concetto di sincronizzazione ... 9

1.2.1 Brevi richiami di teoria dei grafi ... 10

1.2.2 Sincronizzazione di reti dinamiche complesse ... 12

1.2.3 Condizioni di sincronizzazione ... 15

1.2.4 Master Stability Function ... 17

1.3 Caos deterministico ... 20

1.3.1 Caos Deterministico: iterazione di una funzione non lineare... 22

1.3.2 Attrattori ... 23

1.3.3 Attrattori strani, attrattore di Lorenz ... 27

1.4 Il circuito di Chua ... 29

1.4.1 Modello matematico del circuito di Chua ... 31

1.4.2 Dinamiche del circuito di Chua ... 33

1.4.3 Aspetti della sincronizzazione dei circuiti di Chua ... 38

Capitolo 2 ... 42

SETUP SPERIMENTALE E SOFTWARE DI CONTROLLO ... 42

2.1 Il circuito di Chua sperimentale ... 42

2.1.1 L’induttore ... 43

2.1.2 Il diodo di Chua ... 45

2.2 Filosofia del setup sperimentale ... 54

2.2.1 La rete di interconnessione ... 55

2.2.2 Descrizione degli integrati utilizzati ... 59

2.2.3 Il sistema di acquisizione dati... 71

2.3 Il software di controllo ... 73

2.3.1 Virtual instruments ... 76

2.3.2 Descrizione del software realizzato (analisi del front pannel ) ... 78

Capitolo 3 ... 88

SINCRONIZZAZIONE DI 4 CHUA CON LINK DINAMICI ... 88

3.1 La master stability function nel caso di link dinamici ... 88

(6)

II

3.1.2 MSF (caso dinamico) ... 90

3.2 Analisi sperimentale della sincronizzazione ... 101

3.2.1 Topologia della rete utilizzata nell’esperimento e setup utilizzato ... 101

3.2.2 Realizzazione della rete di condensatori di link e resistore res var ... 103

3.2.3 Descrizione delle misure effettuate... 107

3.2.4 Indice di sincronizzazione ... 96

3.2.5 Analisi dei risultati di misura e conclusioni ... 112

3.2.6 Sviluppi futuri ... 117

(7)

1

INTRODUZIONE

Argomento chiave attorno a cui è incentrato questo lavoro di tesi è il concetto di “Caos” e di “Sincronizzazione”.

Negli ultimi anni la comunità scientifica ha concentrato i suoi sforzi allo studio alla formalizzazione ed all’utilizzo di sistemi dinamici non lineari che seppur estremamente più complicati da trattare offrono certamente maggior versatilità rispetto a quelli lineari che possono essere pensati come sottoinsieme dei sistemi non lineari.

D’altronde la maggior parte dei fenomeni naturali e non, mostrano un carattere fortemente non lineare (si pensi ad esempio alla meteorologia, al ferromagnetismo, alle catastrofi, ai sistemi biologici ecc) e quindi si è sempre avvertita la necessità di sviluppare una teoria soddisfacente che spiegasse in maniera quanto più accurata possibile l’evoluzione delle dinamiche di questo tipo di sistemi.

Lo studio di queste dinamiche non lineari ha portato gradualmente allo sviluppo del cosiddetto Caos Deterministico. Questo fenomeno si riscontra solo nei sistemi non lineari e pone dei limiti alla prevedibilità di un sistema complesso non lineare.

Mentre di un sistema lineare si sa tutto ed è possibile prevedere con precisione arbitraria la sua evoluzione, non è altrettanto vero per un sistema non lineare: è sufficiente un piccolissima incertezza sulle condizioni iniziali del sistema per stravolgerne completamente l’evoluzione facendone perdere completamente la sua prevedibilità.

Parallelamente al concetto di Caos è stato introdotto e studiato anche quello di

sincronizzazione.

La sincronizzazione è quel fenomeno per cui due o più sistemi complessi possono in certe condizioni presentare lo stesso comportamento o le stesse dinamiche ovvero si “sincronizzano” fra loro.

(8)

2

Questa proprietà è di fondamentale importanza specialmente nelle applicazioni pratiche come per esempio la realizzazione di un sistema di ricetrasmissione criptato: un trasmettitore genera un segnale portante caotico e quindi rende l’informazione (il segnale modulante) completamente irriconoscibile che può venire decriptato e quindi recuperato solamente da un ricevitore perfettamente sincronizzato al trasmettitore.

In questo lavoro di tesi per generare il Caos in maniera semplice è stato utilizzato un particolare circuito,il circuito di Chua, che sotto opportune condizioni può presentare comportamento o dinamiche “caotiche”.

Oggetto della tesi è la validazione sperimentale di un lavoro teorico condotto sui circuiti caotici di Chua da alcuni docenti operanti presso il Politecnico di Torino sulla ricerca delle soglie di sincronizzazione di reti di Chua con link dinamici. Il lavoro è suddiviso in tre capitoli.

Il primo capitolo tratta degli aspetti teorici del caos, del circuito di Chua e della sincronizzazione ed inoltre introduce la Master Stability Function, un metodo assai efficace per lo studio della sincronizzazione di reti complesse di sistemi caotici.

Il secondo capitolo descrive il prototipo utilizzato per le prove sperimentali, il software di controllo ed il sistema di acquisizione.

Infine il terzo capitolo conclude l’elaborato analizzando e discutendo i risultati di misura ottenuti.

(9)

3

ANALISI SPERIMENTALE DELLA SINCRONIZZAZIONEDI RETI DI CHUA CON LINK DINAMICI

Capitolo 1

SINCRONIZZAZIONE DI RETI COMPLESSE

1.1 Sistemi dinamici

Cominciamo col richiamare brevemente alcune nozioni di Teoria dei Sistemi [1].

Un sistema dinamico è un sistema che evolve nel tempo seguendo una legge ben precisa.

Matematicamente esso è descritto da un sistema di equazioni differenziali ordinarie del tipo:

̇ = = ( , )

dove : → con ⊆ × insieme aperto ed ⊆ è lo spazio delle

fasi.

Si dice soluzione di un sistema dinamico una funzione Ψ: → interpretabile come curva nello spazio delle fasi ed campo vettoriale tangente alla curva.

1.1.1 Stabilità di un sistema dinamico

Consideriamo un sistema dinamico con ingresso ( ) ed uscita ( ).

Diremo che il sistema è stabile in senso BIBO [2] (input

bounded-output) se

| ( )| ≤ ∀ ∈ ⟹ | ( ) | ≤ ∀ ∈

(10)

4

ANALISI SPERIMENTALE DELLA SINCRONIZZAZIONEDI RETI DI CHUA CON LINK DINAMICI Per ogni ( ) limitato, con , ∈

Ancora più forte è la condizione di stabilità secondo Lyapunov. Consideriamo il sistema dinamico

̇ = = ( ( ), ), ( ) =

Definizione (stabilità secondo Lyapunov)

Un punto ̅ si dice stabile secondo Lyapunov se per ogni > 0, ∃ > 0 tale che ∀ sussiste la relazione:

‖ − ̅‖ ≤ ,allora ‖ ( ) − ̅‖ ≤ ∀ ≥ 0

Un punto ̅ si dice asintoticamente stabile se è stabile e se inoltre

lim

→ ‖ ( ) − ̅‖ = 0

Definizione

Sia : ⟶ una funzione scalare. Diremo che è definita positiva se

( ) > 0 ∀ ≠ 0

(11)

5

Teorema

Supponiamo che = 0 sia un punto di equilibrio per il sistema

̇ = = ( ( ), )

Sia : ⊂ ⟶ una funzione differenziabile tale che

( ) = 0 ( ) > 0 − {0} ed V̇(x) = dV(x) dx dx dt ≤ 0 in D

Allora, = 0 è un punto di equilibrio stabile. Inoltre se

V̇(x) ≤ 0 in − {0}

allora = 0 è asintoticamente stabile.

Definizione (stabilità esponenziale)

Un punto si dice esponenzialmente stabile per il sistema se è asintoticamente stabile e se

(12)

6

1.1.2 Esponenti di Lyapunov

Consideriamo [1] il sistema discreto a tempo discreto

( )

e prendiamone una traiettoria con origine in , sia essa { , , … }.

Prendiamo anche la traiettoria originata quando perturbiamo , sia essa

{ , , … }.

Vogliamo valutare di quanto la traiettoria originaria si discosta da quella perturbata.

A tale scopo valutiamo la differenza = − attraverso un sviluppo di Taylor.

= − = ( ) − ( ) = ( ) + ( )

Dopo instanti otteniamo:

= ( ) − ( ) = d

dx[ ( )] + ( ) =

= ( ) + ( )

Trascurando i termini di ordine superiore la relazione si può anche scrivere come:

(13)

7

= ( ) = ⎝ ⎛ ₍ ₎ ⎠ ⎞ = ⎝ ⎛ log ⎝ ⎛ ₍ ₎ ⎠ ⎞ ⎠ ⎞ Al lim → ∞ = ( ) .

La quantità ( ) si definisce esponente di Lyapunov relativa all’orbita . Formalmente la sua definizione è:

( ) = lim →

1

log ( )

Esso ha le dimensioni dell’inverso di un tempo e può essere interpretato come la costante di tempo della dinamica del sistema quando la sua orbita viene perturbata.

Si possono presentare tre casi:

1. ( ) < 0. In questo caso l’orbita perturbata si allontana indefinitamente da quella originaria;

2. ( ) = 0. La distanza fra l’orbita perturbata e quella originaria resta costante;

3. ( ) > 0. L’orbita perturbata tende a ricadere su quella originaria.

(14)

8

Osservazione

La trattazione sugli esponenti di Lyapunov è stata fatta partendo da un sistema a tempo discreto ma sostanzialmente rimane la stessa anche per un sistema a tempo continuo.

In questo caso si parla di “tasso medio” di allontanamento (o di divergenza) delle orbite perturbate.

Definizione alternativa

Sia dato il sistema dinamico di dimensione d.

[ ( )] = ( ; )

→ ( )

+ → ( ) = + ( )

dove ( ) è la traiettoria perturbata.

Linearizzando l’andamento della perturbazione si ottiene:

[ ( )] = ( ) → ( ) = ( ) (0)

Fissato , si definisce esponente di Lyapunov la quantità:

= lim →

1

ln ‖ ( )‖

(15)

9

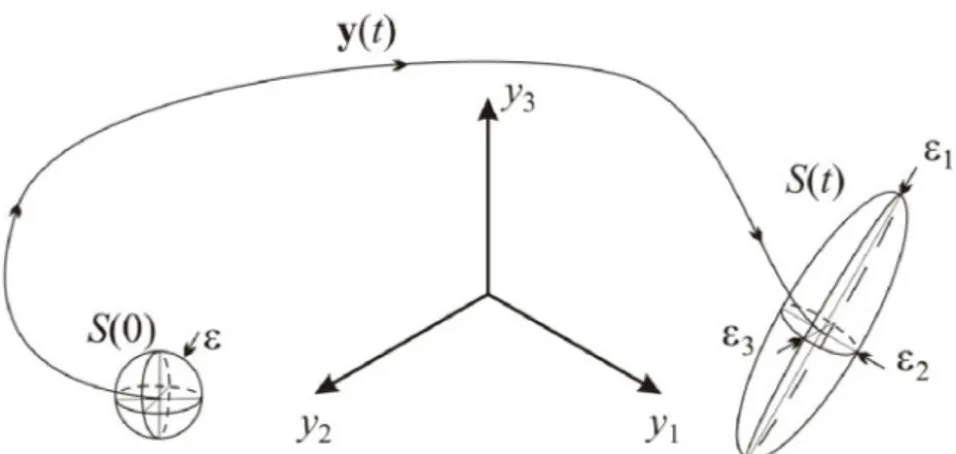
Sia , … … , una base ortonormale per lo spazio di stato. Si definisce Spettro di Lyapunov l'insieme degli d esponenti di Lyapunov ottenuti applicando perturbazioni lungo la base costruita. Lo spettro di Lyapunov è indipendente dalla base considerata

Figura 1-0-1 Interpretazione grafica degli esponenti di Liapunov

( ) = (0) → = 1ln ( )

(0)

L’esponente di Lyapunov costituisce una misura quantitativa della dipendenza di una traiettoria dalle condizioni iniziali. Esso infatti rappresenta il tasso di convergenza (o divergenza) di due traiettorie con condizioni iniziali vicine. Dato un sistema d-dimensionale sarà presente un numero di esponenti di Lyapunov pari alla dimensione dello spazio delle fasi di tale sistema.

1.2 Il concetto di sincronizzazione

La parola sincrono, dal Greco antico σίνχρόνος, vuol dire avvenire contemporaneamente, condividere lo stesso tempo.

Già nel lontano 1673 il fisico Christiaan Huygens [3] scoprì che collegando due masse oscillanti (due pendoli) ad una trave sospesa orizzontalmente sufficientemente rigida era possibile sincronizzarne il moto, ovvero che avvenisse in fase (oppure anche in opposizione di fase).

(16)

10

Egli dedusse che la trave fungeva da variabile di accoppiamento dei due pendoli dal momento che essa compiva piccoli movimenti quasi impercettibili che evidentemente aiutavano la sincronizzazione ma anche che questa condizione era tanto più forte ed immediata quanto più vicine erano le condizioni iniziali dei due pendoli.

Lo studio per questa disciplina ha destato la notevole attenzione da parte della comunità scientifica perché essa ben descrive fenomeni naturali, sociali ecc. Si pensi ad esempio agli stormi di uccelli che cambiano repentinamente direzione tutti insieme, oppure alle lucciole che sincronizzando il loro volo fanno in modo che il loro luccichio pulsi alla stessa frequenza.

1.2.1 Brevi richiami di teoria dei grafi

Lo studio di più sistemi interconnessi, e la loro possibile sincronizzazione, richiede un formalismo di tipo matriciale per la scrittura delle equazioni che ne descrivono il comportamento. [4]

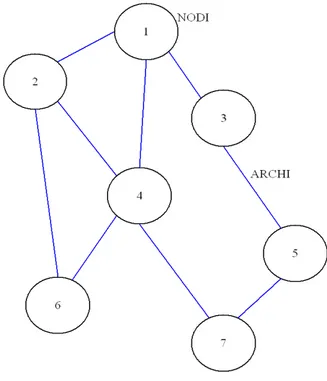
Definiamo grafo un oggetto costituito da vertici ed archi.

I vertici (o nodi) rappresentano la più piccola entità che è possibile studiare da sola, ovvero rappresentano il singolo sistema dinamico autonomamente funzionante.

Gli archi invece sono gli elementi di connessione fra i vari nodi che determinano la topologia della rete. Possono essere bidirezionali e in questo caso vi è una mutua interazione simmetrica fra i nodi, oppure monodirezionali in cui l’interazione e in definitiva l’informazione può fluire solo in un verso.

(17)

11

Figura 1-0-2 Esempio di grafo

Definiamo inoltre grado il numero di archi che afferiscono al nodo. Ad ogni nodo in generale può afferire anche più di un grafo.

Definizione (matrice di adiacenza)

Si definisce matrice di adiacenza ( ) ∈ × dove è il numero di nodi del grafo, la matrice il cui generico elemento è nullo se i nodi , non sono connessi fra loro, mentre vale in generale se i nodi , sono connessi da archi.

Definizione (matrice di grado)

La matrice di grado solitamente indicata con ∈ × = è quella matrice diagonale il cui generico elemento è pari al grado del −simo nodo.

(18)

12

Definizione (matrice di Laplace)

La matrice di Laplace ∈ × si ottiene dalla differenza tra la matrice di grado e quella di adiacenza.

La sua importanza è cruciale ai fini delle proprietà del sistema dinamico che si vuole analizzare.

Si può dimostrare che è simmetrica se anche la matrice di adiacenza è simmetrica, ovvero quindi se la rete è bidirezionale.

Gli autovalori di L sono così ordinati: 0 = < < ⋯ < .

è sempre nullo, mentre il primo autovalore diverso da zero, , determina gran parte delle proprietà dinamiche della rete.

1.2.2 Sincronizzazione di reti dinamiche complesse

È naturale che quando si parla di sincronizzazione si fa riferimento ad almeno due sistemi. [4] [5] [6]

In genere lo studio si affronta considerando N sistemi collegati tra loro in una certa maniera.

Ogni sistema preso singolarmente costituisce un’entità a se stante con le sue proprie leggi e le sue dinamiche, ma quando due o più sistemi vengono interconnessi è chiaro che il sistema da studiare diventa uno solo.

La tipologia dei sistemi ed il modo in cui essi sono collegati fra loro determina il grado di sincronizzazione del sistema risultante.

In genere ci sono molti parametri che influiscono sulla sincronizzazione, tra cui:

 Complessità strutturale, dovuta alle connessioni tra i nodi;

 Evoluzione della rete, ad esempio le connessioni non sono stazionarie nel tempo;

(19)

13

 Diversità dei collegamenti che possono avere peso e tipologia diversi;  Complessità dinamica dei nodi, ad esempio se sono sistemi fortemente

non lineari;

 Diversità dei nodi, ovvero i sistemi posso essere di tipologia diversa.

Si definisce rete dinamica complessa un insieme di nodi interconnessi in cui ogni elemento è funzione in generale funzione della rete stessa.

Ogni nodo costituisce un sistema dinamico di dimensione n, descritto come segue:

̇ = ( ) , = 1,2, … … ,

dove

= { , , … , } ∈

è il vettore trasposto delle variabili di stato del sistema in esame.

Poiché dobbiamo risolvere simultaneamente N sistemi interconnessi allora l’equazione risolvente è:

̇ = ( ) + ( ) = 1,2, … … ,

dove

= { , , … , } ∈

(20)

14

> 0 è detta costante di accoppiamento o anche forza di accoppiamento.

( ) ∶ → è la funzione vettoriale di uscita, mentre i coefficienti sono gli elementi della matrice di connettività ∈ R × . Questa matrice ha la proprietà di avere la somma delle righe sempre nulle ( ∑ = 0, ∀ ) e termini strettamente negativi lungo la diagonale principale

( < 0, ∀ ).

Ora supponiamo che i sistemi da studiare siano tutti uguali e quindi ( ) =

( ).

Possiamo quindi riscrivere l’equazione risolvente del sistema come:

̇ = ( ) − = 1,2, … … ,

è una matrice diagonale i cui elementi specificano attraverso quali variabili di stato avviene l’accoppiamento fra i sistemi.

Si ha ad esempio:

γ = 1 → accoppiamento sulle prime variabili di stato { , , … , } γ = 1 → accoppiamento sulle seconde variabili di stato { , , … , }

I coefficienti sono i coefficienti della matrice di Laplace definita nel paragrafo precedente.

Se è presente una connessione tra il nodo k e il nodo j, allora il generico elemento

= −1, altrimenti = 0 ≠ . Gli elementi sulla diagonale principale di L sono

(21)

15

= − ,

, = 1,2, … . . ,

Se inoltre il nodo k-esimo ha grado , gli elementi sulla diagonale principale possono essere scritti come:

= , = 1,2, … . . ,

1.2.3 Condizioni di sincronizzazione

Diremo che una rete dinamica è asintoticamente sincronizzata se:

lim

→ ( ) − ( ) = 0, ∀ , ( ≠ )

cioè al crescere del tempo i segnali ai vari nodi avranno lo stesso andamento. La condizione di sincronizzazione prevede che:

( ) = ( ) = … = ( ) = ( ) , → ∞

e quindi tutte le traiettorie convergeranno allo stato sincrono ( ) per cui preso un nodo isolato vale l’identità:

̇ ( ) = ( ( ))

dove ( ) può essere un punto di equilibrio, un’orbita periodica o un attrattore caotico.

(22)

16

̇ = ( ) − = 1,2, … … ,

Siano

0 = < < ⋯ <

gli autovalori della matrice di di Laplace associata alla rete. Supponiamo che

esista una matrice diagonale quadrata di dimensione × e due costanti u < 0 e τ > 0 tali che:

[ ( ( )) + ] + [ ( ( )) + ] ≤ −

∀ ≤ u , con ∈ × .

Se risulta

≤ u

allora lo stato di sincronizzazione ( ) della rete è esponenzialmente stabile. Poiché però < 0, allora:

≥ u

Poiché un numero negativo molto piccolo ha un valore assoluto molto grande allora significa che la rete può anche sincronizzarsi con una bassa forza di accoppiamento.

(23)

17

1.2.4 Master Stability Function

Uno dei migliori metodi per l’analisi e lo studio della sincronizzazione di sistemi dinamici è la Master Stability Function proposta da Louis M. Pecora nel 1988. [6] [7] [8]

Graficamente essa viene valutata al variare di un parametro di accoppiamento opportunamente normalizzato, k, ottenuto dal prodotto tra la costante di accoppiamento c e l’autovalore λ2.

Condizione necessaria per ottenere sincronizzazione è che la MSF sia negativa

al crescere del parametro k.

Esistono tre diverse tipologie di MSF:

1. MSF di tipo I. La funzione è inizialmente positiva per poi decrescere fino a diventare negativa in corrispondenza di un certo k.

2. MSF di tipo II. La funzione è inizialmente positiva, diventa negativa in corrispondenza di un certo per poi ridiventare positiva in

corrispondenza di un certo , < .

3. MSF di tipo III. La funzione è inizialmente negativa per poi assumere a partire da un certo valori positivi.

Nel nostro caso la MSF è di tipo I, per cui avremo che il sistema è sincronizzato (lo stato sincrono è asintoticamente stabile) a partire dal valore k in corrispondenza del quale la MSF diviene negativa. Vediamo ora come è possibile ricavare l’espressione grafica della MSF al variare del parametro di accoppiamento k.

Consideriamo un sistema composto da N oscillatori non lineari accoppiati. Ogni oscillatore, quando isolato, è descritto dall’equazione:

(24)

18

ANALISI SPERIMENTALE DELLA SINCRONIZZAZIONEDI RETI DI CHUA CON LINK DINAMICI ̇ = ( )

dove x è un vettore d-dimensionale e F(x) una funzione generalmente non lineare.

Se invece consideriamo che ogni oscillatore interagisce con gli altri N-1 oscillatori, avremo che l’equazione che descrive il singolo oscillatore accoppiato diviene:

̇ = ( ) − , = 1,2, … … .

dove è il vettore di stato dell’oscillatore k-esimo, c la costante di accoppiamento.

Quando tutti i nodi saranno in sincronizzazione le grandezze di stato avranno praticamente lo stesso andamento e quindi la soluzione sarà unica. Essa sarà:

= = … … . = =

Supponiamo ora che l’oscillatore sia accoppiato e perturbiamo di poco la sua soluzione di equilibrio ( ):

= ( ) −

dove ( ) = [ ( ) − ( )] e ( ̅) è la matrice iacobiana di ( ( )). Una volta diagonalizzata la matrice e calcolati un insieme di autovalori reali

(25)

19

ed i rispettivi autovettori

( ∶ = 1, 2 … . . , )

si può porre = ̿ dove ̿ è una matrice che ha per colonne gli autovettori di .

Otteniamo quindi:

= [ ̿ ( ) − ]

Ponendo = = 1, 2, … . , si può riscrivere l’equazione precedente come:

= [ ̿ ( ) − ]

Da quest’ultima equazione si possono calcolare gli esponenti di Lyapunov e il più grande di questi è la Master Stability Function Λ(k).

Calcolare la MSF per un sistema da sincronizzare vuol dire calcolare gli autovalori della matrice ̿ ( ) − che però presenta una dipendenza dallo stato sincrono ( ).

Non è quindi possibile calcolarli in forma chiusa ma bisogna ricorrere a delle tecniche numeriche.

Il MATLAB in questo caso rappresenta un ottimo strumento per il calcolo degli autovalori.

(26)

20

1.3 Caos deterministico

La teoria del Caos Deterministico è stata sviluppata per l’esigenza di poter descrivere con accuratezza le dinamiche di sistemi non lineari quando ci si rese conto che i modelli fisico-matematici allora conosciuti mal descrivevano dinamiche di fenomeni complessi quali il moto dei pianeti, il moto di un pendolo, le distribuzione delle correnti atmosferiche ecc.

Pioniere di tale teoria fu il fisico Edward Lorenz. [9]

Il 29 dicembre del 1979, in occasione della Conferenza annuale dell’ American

Association for the Advancement of Science egli presentò un documento

suscitando notevole interesse da parte della comunità scientifica.

In particolare Lorenz ipotizzava che un “lieve” battito d’ali di una farfalla in Brasile potesse provocare un evento climatico catastrofico in Texas.

A questo insolito documento fu dato il nome di effetto farfalla (butterfly effect). Durante una simulazione numerica del clima Lorenz fece una entusiasmante scoperta.

Utilizzando un modello non lineare di previsione atmosferica si accorse che variando di una piccola quantità le condizioni iniziali nelle varie simulazioni, i risultati ottenuti erano profondamente diversi fra di loro.

Sulla base di queste osservazioni fu avviato lo studio sistematico della Teoria del Caos Deterministico.

Mentre nei sistemi lineari, una piccola variazione nello stato iniziale di un sistema provoca una variazione corrispondentemente piccola nello stato finale, non è altrettanto vero per i sistemi non lineari nei quali piccole differenze nelle condizioni iniziali producono differenze non prevedibili nel comportamento successivo.

Quindi è del tutto impossibile prevedere l’evoluzione di un sistema non lineare perché un piccolo errore nella misurazione delle condizioni iniziali unito al

(27)

21

problema dell’arrotondamento dei valori delle grandezze durante il calcolo numerico conduce a risultati completamente diversi da quelli attesi.

Teoricamente il problema potrebbe essere risolto misurando con incertezza nulla i dati relativi alle condizioni iniziali, ma questo è impossibile dal punto di vista pratico perché uno strumento di misura per quanto prestante sia introdurrà sempre e comunque un’incertezza sul valore misurato.

La parola Caos Deterministico non deve trarre in inganno. Si potrebbe pensare infatti che il notevole cambiamento delle traiettorie del sistema al variare delle condizioni iniziali sia dovuto ad una forte componente stocastica intrinseca al sistema stesso, invece i modelli dei sistemi sono assolutamente deterministici, ovvero non sono descritti da variabili aleatorie.

In molte discipline lo studio del Caos ha dato ottime conferme sul fatto che la maggior parte dei fenomeni è di tipo non lineare. L’evoluzione dei fenomeni naturali non procedono con ritmi periodici, ma, dopo un periodo di regolarità, presentano in modo inaspettato una biforcazione in un punto critico che si moltiplica fino a generare un comportamento turbolento.

Alla luce di quanto esposto possiamo dunque affermare che un sistema

dinamico si dice caotico se presenta le seguenti caratteristiche:

• Sensibilità alle condizioni iniziali: a variazioni infinitesime delle condizioni al contorno (o, genericamente, degli ingressi) corrispondono variazioni finite in uscita;

• Imprevedibilità: non si può prevedere in anticipo l’andamento del sistema su tempi lunghi rapportati al suo tempo caratteristico, a partire da assegnate condizioni al contorno;

• L’evoluzione del sistema è descritta, nello spazio delle fasi, da innumerevoli

(28)

22

Si definisce allora il Caos come un comportamento non predicibile di un

sistema dinamico deterministico a causa della sua sensibilità alle condizioni iniziali o meglio come un comportamento aperiodico a lungo termine in un sistema deterministico caratterizzato da una alta dipendenza alle condizioni iniziali.

1.3.1 Caos Deterministico: iterazione di una funzione non lineare

Facciamo un esempio di sistema dinamico che renda bene l’idea di quanto appena affermato.

Supponiamo di voler iterare una funzione non lineare, ad esempio di tipo quadratico.

Consideriamo ad esempio il sistema:

= ( ) = − 2

Riportiamo i valori delle prime N iterazioni su di un grafico (ottenuto con Labview) scegliendo come condizione iniziale lo stato =1.5

(29)

23

Ora scegliamo un valore leggermente diverso per lo stato iniziale, =1.501

Figura 1-0-4 Iterazione della funzione per x0 = 1.501

Si nota subito che il sistema ha lo stesso comportamento fino N = 5, dopodiché già da N = 10 ha un andamento molto diverso. È bastato un aumento dell’un per mille della condizione iniziale per produrre una serie di risultati completamente diversi.

Questo è un semplice esempio di Caos Deterministico.

1.3.2 Attrattori

Un attrattore [10] [11] è un insieme (ad esempio un punto, una curva nello spazio od anche una varietà differenziabile) verso il quale un sistema dinamico tende al crescere del tempo.

Se questo insieme ha una struttura tipicamente frattale allora l’attrattore sarà detto strano.

Ricordiamo che per soluzione di un sistema dinamico

(30)

24

con funzione differenziabile, si intende l’insieme di tutte le traiettorie in funzione delle condizioni iniziali. Lo spazio delle fasi o degli stati è quel campo vettoriale le cui componenti sono proprio le variabili di stato del sistema.

Al variare del tempo l’estremo libero di questo vettore descriverà una

traiettoria nello spazio delle fasi e quindi la soluzione del sistema.

Il sistema si dice deterministico se per ogni stato esiste un’unica soluzione,

stocastico se l’insieme delle soluzioni è descritto da una variabile aleatoria.

Definizione (punto fisso)

Sia dato il sistema dinamico

̇ = = ( , )

e supponiamo che ( ) = .

Diremo che è un punto fisso del sistema se ( ) = 0.

Ad esempio un punto fisso può essere un attrattore per un pendolo smorzato in cui, a causa dell’attrito sulla cerniera e dell’attrito viscoso della massa oscillante nel fluido in cui è immersa porta il sistema ad avere sia posizione che velocità nulle.

Definizione (traiettoria omoclìna)

Una traiettoria ( ) è detta omoclìna se esiste punto fisso tale che:

lim

(31)

25

Definizione (punto limite)

Diremo che è un punto limite per la traiettoria ( ) se:

∀ > 0, ∀ ∃ > ℎ ‖ ( ) − ‖ <

Osservazione 1

Supporremo sempre che le traiettorie siano sempre uniformemente limitate e cioè che esista una regione chiusa dello spazio delle fasi in cui tutte le traiettorie permangono per un tempo indefinito.

Un sottoinsieme di uno spazio metrico chiuso e limitato è compatto, e quindi per il teorema di Bolzano-Weierstrass ogni traiettoria ammette almeno un punto limite.

Osservazione 2

Supponiamo che la traiettoria ( ) abbia un punto limite in .

Allora tutti i punti che giacciono sulla traiettoria passante per sono punti limite per ( ).

Definizione (valore limite)

Data una successione { , ∈ }, se esiste una sottosuccessione { } convergente ad un punto ∗, allora ∗è un valore limite.

La stessa definizione vale anche per una funzione ( ), ∈ , ovvero se esiste una successione di valori della variabile indipendente tale che lim _→ =

∗_{e lim}

(32)

26

Supponiamo ora che una certa soluzione ( ) di un sistema dinamico rimanga sempre confinata in un compatto ⊂ con spazio delle fasi.

Possiamo assumere che questa soluzione sia un’orbita, ovvero sia definita per ogni ∈ a patto che tutte le successioni di punti ( ) → ∞, devono avere delle sottosuccessioni convergenti, cioè devono esistere dei valori limite per

( ) → ∞.

Definizione (ω-limite α-limite)

Dato un sistema dinamico, l'insieme dei valori limite di un'orbita ( ) per → ∞ si chiama insieme ω-limite dell'orbita. L'insieme dei valori limite per → −∞ si chiama insieme α-limite.

Si parla di valori limite soltanto quando non è necessario stabilire i due casi.

Definizione (orbita periodica, ciclo limite)

Una soluzione ( ) di un sistema dinamico si dice orbita periodica se esiste un numero ≠ 0 tale che

( + ) = ( ) ∀ ∈ .

Il più piccolo di tali si dice periodo dell'orbita periodica.

Per le orbite periodiche ogni punto della traiettoria è un valore limite ovvero

( ) = lim

(33)

27

Quindi l’insieme ω-limite coincide con la traiettoria. Stesso discorso vale per l’insieme α-limite.

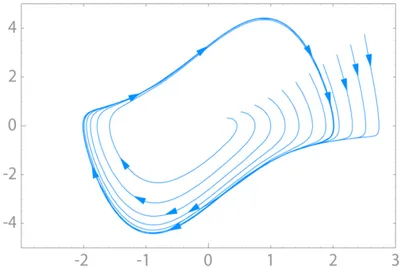
Se l’insieme dei punti percorsi da un’orbita periodica funge da ω-limite (oppure

α-limite) per un’orbita diversa, allora siamo in presenza di un ciclo limite.

Figura 1-0-5 Ciclo limite

1.3.3 Attrattori strani, attrattore di Lorenz

Se una traiettoria ha una topologia frattale oppure la dinamica sulla traiettoria è caotica allora si parla di strano attrattore.

Un classico esempio di strano attrattore dovuto ad una dinamica caotica è l’attrattore di Lorenz.

Il modello di Lorenz nasce nel 1963 da alcune sostanziali semplificazioni delle equazioni di Navier-Stokes sulla descrizione del comportamento dinamico di uno strato di fluido che presenta moti convettivi a causa di una differenza di temperatura applicata fra la superficie inferiore e quella superiore. Il modello è costituito da un sistema di tre equazioni differenziali di primo ordine in forma normale nelle variabili ( , , ).

(34)

28

⎩ ⎪ ⎨ ⎪ ⎧ = ( , , ) = ( − ) = ( , , ) = − − = ( , , ) = −

Lo spazio delle fasi è tridimensionale, e le variabili ( , , ) non sono variabili spaziali: la variabile è legata al campo di velocità del fluido, la variabile è proporzionale alla differenza di temperatura tra le correnti ascendenti e quelle discendenti, e è proporzionale alla distorsione dalla linearità de profilo verticale di temperatura.

σ, b ed r sono parametri idrodinamici che possono assumere solo valori positivi.

Durante lo studio di questo sistema Lorenz si accorse di un andamento non periodico, mentre allora si riteneva che il comportamento tipico di un qualunque sistema di equazioni differenziali fosse periodico. Nel ricontrollare i dati ottenuti fino all’istante T, decise di ripetere l’integrazione numerica, e per risparmiare tempo non scelse la condizione iniziale { (0), (0), (0) } ma un punto intermedio ∗ < , le cui coordinate erano già state stampate dal calcolatore. Ovviamente si aspettava di ritrovare gli stessi punti già ottenuti nell’intervallo [ ∗, ] Ciò che osservò fu, invece, che le due traiettorie si sovrapponevano per un certo tempo, per poi divergere progressivamente e diventare completamente diverse. Egli attribuì la causa di questa discrepanza non agli errori di integrazione, ma soltanto a valori iniziali leggermente diversi: mentre nella prima integrazione il punto { ( ∗), ( ∗), ( ∗) } era stato memorizzato con sei cifre significative, nel ripetere l’integrazione, la seconda volta, Lorenz ne ricopiò soltanto tre.

(35)

29

Figura 1-0-6 Attrattore di Lorenz

1.4 Il circuito di Chua

Figura 1-0-7 Il Prof Leon Ong Chua

Il circuito di Chua [12] costituisce uno dei circuiti non lineari più semplici che sotto opportune condizioni presenta un comportamento caotico.

Nel 1983 il Prof. Leon Ong Chua, docente dell’università di Berkeley in California, mise a punto un circuito non lineare (da lui stesso battezzato circuito di Chua).

Il suo funzionamento fu accertato e studiato da un altro professore, Matsumoto [13], che mediante simulazioni numeriche riuscì a dimostrarne l’intrinseca caoticità.

(36)

30

Si tratta in sintesi di un oscillatore autonomo che, nel corso degli anni, è stato ampiamente investigato da tutta la comunità scientifica in virtù del fatto di essere l’unico circuito autonomo in cui la presenza del caos è stata provata in maniera esatta, tanto da essere definito “a universal paradigm for chaos”.

La versione più semplice ed economica del circuito di Chua fu proposta da Michael Peter Kennedy che, come vedremo più avanti utilizza particolari circuitazioni sia per l’induttore che per il resistore non lineare.

Figura 1-0-8 Circuito di circuito di Chua

L’oscillatore è fondamentalmente costituito da tre bipoli reattivi (due condensatori C1 e C2 ed un induttore L), un resistore lineare R ed infine un resistore non lineare R detto anche Diodo di Chua, cuore del sistema, che ne determina un comportamento caotico.

Quindi le variabili di stato del circuito sono tre ovvero la corrente nell’induttore e le tensioni ai capi dei due condensatori che come sappiamo sono legate alle energie immagazzinate rispettivamente nel campo magnetico e nel campo elettrico: = 1 2 ( ) =1 2 ( ) [ ]

(37)

31

1.4.1 Modello matematico del circuito di Chua

Per capire come funziona il circuito di Chua dobbiamo scrivere le equazioni che ne governano la dinamica.

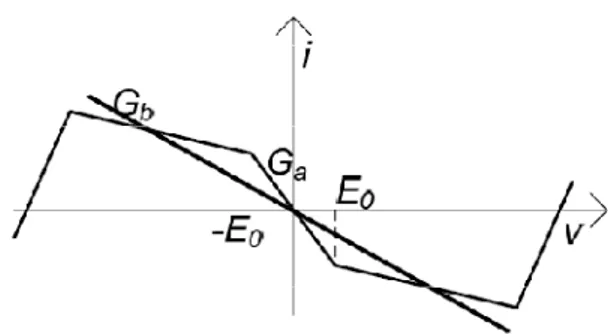
Cominciamo col descrive la caratteristica tensione-corrente del resistore non

lineare R.

Figura 1-0-9 Caratteristica I-V del Diodo di Chua

Si tratta di una caratteristica lineare a tratti e quindi complessivamente non lineare.

La sua espressione analitica è la seguente:

( ) =

+ ( − ) , ≤ −

, | | ≤

+ ( − ) , ≥

Dove , sono le pendenze dei tratti interni ed esterni alla caratteristica rispettivamente.

Applicando le leggi di Kirchoff al circuito di figura 1-7 otteniamo:

(38)

32

= 1 [ ( − ) + ]

= −1

dove ( ) è proprio la caratteristica I-V del Diodo di Chua scritta prima, mentre , sono le tensioni ai capi dei condensatori e la corrente nell’induttore rispettivamente.

Possiamo definire della nuove grandezze adimensionalizzate al fine di ottenere delle espressioni analiticamente più semplici.

Si definisce: = ; = ; = ( ); = ; = ; = ; = ; = ( );

Le equazioni del circuito di Chua allora si riscrivono come:

̇ = [ − − ( )]

̇ = − +

̇ = −

(39)

33

ANALISI SPERIMENTALE DELLA SINCRONIZZAZIONEDI RETI DI CHUA CON LINK DINAMICI mentre

( ) =

+ − , ≤ −1 , | | < 1

+ − , ≥ 1

è una funzione lineare a tratti. Se definiamo ancora

ℎ( ) = + ( ) = +1

2( − )(| + 1| − | − 1|)

con = + 1 = + 1

allora possiamo riscrivere le equazioni della dinamica del circuito come:

̇ = [ − ℎ( )]

̇ = − +

̇ = − Tali equazioni sono dette equazioni di Chua.

1.4.2 Dinamiche del circuito di Chua

Intersecando la caratteristica del diodo di Chua con la retta di pendenza pari a −1 _{si ottengono i punti di equilibrio in continua del circuito di Chua.}

(40)

34

Figura 1-0-10 Itersezione della caratteristica I-V del Chua con la retta di pendenza -1/R

Il resistore di Chua R (oppure il parametro ), è un parametro di fondamentale importanza per questo circuito che ne determina in sintesi la sua dinamica.

Al variare di esso si ottengono comportamenti molto differenti fra loro è quindi si tratta di un parametro di biforcazione.

Variando R però si ottiene che anche i punti di equilibrio della regione esterna alla caratteristica variano e quindi volendoli mantenere gli stessi occorre variare

tenendo costante R.

Se varia varia parimenti ma questo non costituisce un problema perché il parametro non contribuisce alla determinazione dei punti di equilibrio del sistema.

Tuttavia si preferisce variare R dal momento che è molto più semplice dal punto di vista pratico.

Al variare di R, utilizzando un oscilloscopio in modalità XY è possibile visualizzare i vari attrattori generati dalle traiettorie riportando semplicemente due delle tre variabili di stato del circuito di Chua.

Tipicamente si scelgono le tensioni ai capi dei condensatori.

Riportiamo brevemente una discussione qualitativa di quello che accade al variare di R.

1. Per R sufficientemente grande si ha che i punti di equilibrio delle regioni esterne sono stabili, mentre l’origine è un punto di equilibrio instabile. Il

(41)

35

sistema si porterà quindi, a seconda del suo stato iniziale, su uno dei punti di equilibrio stabile per rimanervi indefinitamente. Se ci si pone in un punto della regione interna, la traiettoria si allontanerà in modo esponenziale dall’origine in direzione delle regioni esterne dove l’effetto dell’autovalore negativo costringerà la traiettoria ad avvolgersi a spirale nel punto di equilibrio della stessa regione. In poche parole, la traiettoria si adagia su uno dei punti di equilibrio delle zone esterne.

2. Diminuendo R, la parte negativa degli autovalori complessi delle regioni esterne diminuisce e crescerà il tempo necessario all’orbita per portarsi in uno dei punti di equilibrio stabile. Allora la traiettoria passa dalla regione esterna a quella interna e da questa nuovamente in quella esterna di partenza, dando così origine ad un’orbita periodica che esegue un solo giro intorno al punto di equilibrio instabile: il cosiddetto ciclo limite 1T.

Figura 1-0-11 Attrattore periodico,ciclo limite 1T

3. Diminuendo ulteriormente la resistenza R, si arriva a dei valori per i quali si ottiene la biforcazione di Hopf: In corrispondenza di essa i punti di equilibrio delle regioni esterne perdono la loro stabilità e i punti instabili del sistema passano da uno a tre. La nuova situazione che si viene a creare tuttavia, pur modificando totalmente il comportamento delle regioni

(42)

36

esterne, non altera quello della regione interna. Tale biforcazione, portando duplicazione del periodo, consente all’orbita di eseguire prima due e successivamente quattro giri attorno alla instabilità. Questi cicli vengono detti ciclo limite 2T e ciclo limite 4T

Figura 1-0-12 Biforcazione della traiettoria,ciclo limite 2T

4. Passando ad un valore di R ancora inferiore, i cicli diventeranno allora 8, 16, 32 e così via fino a raggiungere, al limite, infiniti cicli dell’orbita. Questa situazione corrisponde ad uno strano attrattore, detto strano

attrattore a spirale di Chua. Esso rappresenta l’esempio più semplice nello

spazio delle fasi di un regime caotico.

(43)

37

5. Diminuendo ulteriormente la resistenza appaiono diversi attrattori di questo tipo separati uno dall’altro tramite zone ambigue. Si osserva, cioè, che l’orbita esegue un fissato numero di giri attorno al suo punto instabile poi passa nella zona interna della linearità dell’elemento non lineare dove compie a sua volta una spirale attorno alla sua instabilità per poi ritornare nella zona di partenza. Le due spirali si uniranno pertanto nel formare questo nuovo tipo di attrattore chiamato Attrattore Double Scroll.

Figura 1-0-14 Attrattore caotico Double Scroll

6. Continuando a diminuire R si osserva ancora un attrattore caotico di tipo double scroll. Tuttavia per taluni valori di R, l’orbita caotica può mostrare condizioni di periodicità di periodo 8, periodo 16, e così via: sono le cosiddette finestre nel caos.

(44)

38

Figura 1-0-15 Finestra nel caos

7. Infine si ottiene il limite critico. Diminuendo ancora il valore di R si ottiene una instabilità generale del sistema. Ciò porterebbe l’orbita ad una divergenza a spirale verso l’infinito (condizione di saturazione).

Figura 1-0-16 Limite critico di saturazione

1.4.3 Aspetti della sincronizzazione dei circuiti di Chua

Due o più oscillatori di Chua si dicono sincronizzati quando pur partendo da condizioni iniziali diversi fra loro raggiungono uno stato comune, sia esso caotico o meno.

Come già detto prima, il collegamento fra più reti o nodi può essere bidirezionale e monodirezionale.

(45)

39

Se il collegamento è bidirezionale è chiaro che non è possibile parlare di sistema

“pilotante” e sistema “pilotato”perché lo scambio di energia fra i due nodi può

avvenire in entrambe le direzioni.

Intuitivamente potremmo dire che entrambi i sistemi sono contemporaneamente master e slave!

Nel caso di collegamento monodirezionale viceversa è possibile parlare di sistema master e slave dal momento che l’informazione e quindi l’energia ad essa associata fluisce in un senso soltanto.

L’accoppiamento monodirezionale è anche chiamato accoppiamento

drive-response.

Consideriamo per prima questo tipo di collegamento e prendiamo il caso in cui la variabile x viene usata per pilotare il sistema “slave”.

Le equazioni sono: ̇ = [ − ℎ( )] ̇ = − + ̇ = − ̇ = − ′ + ̇′ ′̇ = − ′

e questo è lo schema circuitale che lo realizza.

(46)

40

Notiamo la presenza di un amplificatore operazionale montato in configurazione ad inseguitore di tensione. La sua funzione è quella di “forzare” la prima variabile di stato del primo circuito sulla variabile di stato ′ del secondo circuito ma non il viceversa.

Gli esponenti di Lyapunov condizionali del sottosistema (in questo caso lineare) hanno parte reale negativa: di conseguenza i due circuiti sincronizzano.

Stessa cosa succede se prendiamo come variabile di pilotaggio la tensione sul secondo condensatore . ̇ = [ − ℎ( )] ̇ = − + ̇ = − ′̇ = [ − ℎ( ′)] ′̇ = −

Ecco lo schema circuitale

Figura 1-0-18 Accoppiamento tramite la tensione V2

Per quanto riguarda invece la variabile z, se la si utilizza per pilotare il sistema “slave” si hanno esponenti a parte reale positiva e quindi non si può raggiungere la sincronizzazione.

Nel caso di accoppiamento bidirezionale si può usare questo tipo di schema circuitale.

(47)

41

Figura 1-0-19 Accoppiamenti bidirezionali a)tramite V1; b)tramite V2

Le rispettive equazioni adimensionalizzate nel caso a) sono:

̇ = [ − ℎ( )] + ( − ) ̇ = − + ̇ = − ′̇ = [ − ℎ( ′)] + ( − ) ′̇ = − ′ dove =

Mentre nel caso b) diventano:

̇ = [ − ℎ( )] ̇ = − + + ( − ) ̇ = − ̇ = [ − ℎ( )] ̇ ′ = ′ − ′ + ′ + ( − ) ′̇ = − ′ dove =

(48)

42

Capitolo 2

SETUP SPERIMENTALE E SOFTWARE DI CONTROLLO

Nel seguente capitolo sarà descritto il setup sperimentale realizzato per studiare la sincronizzazione di reti costituite da 4 o 8 circuiti di Chua.

La bontà della sincronizzazione sarà accertata valutando un particolare indice (indice di sincronizzazione) di cui si parlerà nel terzo capitolo.

Il capitolo inizierà con una descrizione del singolo circuito di Chua utilizzato nell’esperimento e delle sue parti principali (induttore e diodo di Chua).

Successivamente verrà presentato lo schema a blocchi del setup realizzato mettendone in risalto la sua logica ed il suo funzionamento in vista degli obbiettivi prefissati.

Infine seguirà una trattazione accurata dei singoli blocchi costituenti e del software di gestione.

2.1 Il circuito di Chua sperimentale

Nel circuito utilizzato nelle prove sperimentali i due condensatori C1 e C2 sono degli ordinari condensatori al poliestere.

L’induttore, e soprattutto il Diodo di Chua, necessitano di una descrizione più approfondita.

Il classico induttore è costituito da un solenoide, avvolto tipicamente in aria oppure su un supporto di materiale ferromagnetico se si vuole raggiungere un valore del coefficiente di autoinduzione maggiore.

Ma entrambe le soluzioni sono state scartate perché nel primo caso, ovvero con solenoide avvolto in aria, si sarebbe ottenuto un induttore troppo ingombrante con parametri parassiti non trascurabili come per esempio una resistenza serie

(49)

43

dovuta al filo conduttore troppo alta ed alti valori di flusso magnetico disperso con conseguente calo del coefficiente di bontà del componente.

Ma anche la seconda soluzione è stata accantonata perché avremmo ottenuto un induttore sicuramente più piccolo del precedente ma purtroppo non lineare, non linearità che come sappiamo è dovuta al ciclo di isteresi del ferro.

2.1.1 L’induttore

La migliore soluzione per la realizzazione pratica dell’induttore è stata quella di utilizzare un circuito giratore (proposto da Kennedy) [14]. Nella sua versione più semplice un circuito giratore è costituito da un condensatore, due resistori ed un amplificatore operazionale U1 collegati secondo lo schema elettrico seguente: RL R C Zin Figura 2-0-1 Giratore

Questo circuito presenta un comportamento induttivo tra il morsetto e massa e il suo funzionamento si basa sull’effetto di inversione della impedenza capacitiva.

L’impedenza desiderata è del tipo = ( + ).

Scrivendo le equazioni di Kirchoff alle maglie e ai nodi del circuito e tenendo presente il concetto di corto circuito virtuale valido per un amplificatore

(50)

44

operazionale ideale si ottiene una relazione del tipo = ( + )

valida nell’ipotesi che ≫ . L’impedenza equivalente è quindi:

L RL

Zin

Figura 2-0-2 Impedenza equivalente del circuito giratore

dove = .

Nel nostro setup sperimentale è stata invece usata una versione più raffinata dei circuito giratore.

(51)

45

ANALISI SPERIMENTALE DELLA SINCRONIZZAZIONEDI RETI DI CHUA CON LINK DINAMICI Il valore di induttanza offerta dal circuito è calcolabile con la formula:

=( )

2.1.2 Il diodo di Chua

Il diodo di Chua rappresenta il cuore di tutto sistema, quello che ne rende caotico il suo comportamento. È realizzato mediante amplificatori operazionali collegati opportunamente di cui riportiamo brevemente il punti salienti del loro funzionamento. U1 +Vcc -Vcc Vin-Vin+ Vout

Figura 2-0-4 Amplificatore operazionale

Si definisce Amplificatore Operazionale un dispositivo elettronico con due morsetti di ingresso , chiamati rispettivamente ingresso invertente ed ingresso non-invertente ed un morsetto di uscita la cui caratteristica di

(52)

46

( ) = ⎩ ⎪ ⎨ ⎪ ⎧− , ≤− , | | ≤ − + , ≥ +

Le tensioni , , ± , sono riferite a massa ed = ( − )

.

è la tensione in corrispondenza della quale l’uscita satura. Essa dipende sia dal particolare circuito in cui è inserito il dispositivo ma soprattutto dalla tensione di alimentazione dell’operazionale ± .

La regione in cui ( ) = e quindi vi è diretta proporzionalità tra la tensione applicata e la tensione di uscita è detta regione di linearità ed il parametro è detto guadagno open loop.

Nel caso ideale questo dispositivo presenta una impedenza di ingresso infinitamente grande, una impedenza di uscita rigorosamente nulla, ed un guadagno infinitamente grande.

Con queste posizioni possiamo assumere nulle anche le correnti in ingresso all’amplificatore operazionale.

Passiamo ora alla descrizione del componente più importante di tutto il sistema. Come già detto precedentemente, dobbiamo realizzare un dispositivo lineare a tratti a cinque spezzate. Poiché alcuni di questi tratti hanno una pendenza negativa e quindi il loro comportamento è del tipo a resistenza negativa, dobbiamo dapprima capire come realizzare un bipolo che possa presentare un simile comportamento.

Ricordiamo brevemente il concetto di resistenza differenziale.

Supponiamo di avere un bipolo con una certa caratteristica tensione-corrente non necessariamente lineare, sia essa ad esempio quella mostrata in figura

(53)

47

Figura 2-0-5 Caratteristica I-V di un bipolo non lineare

In generale, in un tipo di bipolo come questo, la corrente che in esso fluisce è una funzione piuttosto complicata della tensione applicata ai suoi capi, si pensi ad esempio alle lampade a scarica oppure al diodo Esaki.

In questo caso non è più possibile parlare di resistenza del bipolo, ma quello che si può fare è mettersi in un punto preciso della caratteristica ad esempio il punto Q e considerare intorno ad esso una variazione ∆ della tensione applicata e leggere la corrispondente variazione di corrente che essa provoca ∆ .

Si definisce resistenza differenziale il seguente limite: lim ∆ → ∆ ∆ = ∂V ∂I

ovvero non è altro che la derivata della tensione rispetto alla corrente nel punto considerato.

Se la caratteristica del bipolo non è monotòna allora può accadere che tale limite risulti negativo per alcuni valori di tensione e corrente e quindi questo significa

(54)

48

che ad un aumento della tensione applicata si verifica una diminuzione della corrente. Allora in questo caso diciamo che il bipolo presenta una resistenza differenziale negativa.

Tale comportamento è anche quello del Diodo di Chua.

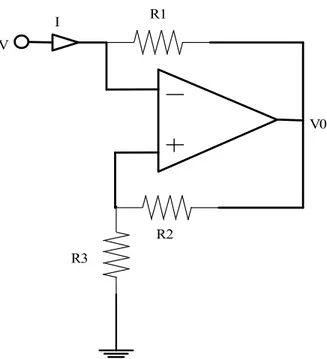
Sono molte le tecniche che consentono di avere bipoli con tale caratteristica. Una della più semplici è quella di utilizzare proprio gli amplificatori operazionali. Eccone un esempio: R1 R2 R3 V I V0

Figura 2-0-6 Realizzazione di una resistenza negativa

L’analisi del sistema si effettua in condizioni di idealità ovvero considerando nulle le correnti all’ingresso dell’amplificatore operazionale ed un guadagno open loop infinito.

Sotto queste ipotesi la corrente i si scrive come:

= −

(55)

49

+[ + (1 + )]

( + )

dove è la differenza di tensione tra il morsetto non invertente e quello invertente.

Considerando → ∞ ed = si ottiene:

= − 1

e quindi proprio una caratteristica lineare a resistenza negativa.

Nell’analisi non abbiamo tenuto conto degli effetti di saturazione che però ora non possiamo più trascurare. Infatti ci dobbiamo aspettare che non è possibile variare a piacimento la tensione di ingresso ottenendo una qualsivoglia corrente i ma ad un certo punto interverrà il fenomeno di saturazione dell’amplificatore operazionale.

Consideriamo ad esempio la saturazione positiva = + . Otteniamo quindi:

= − (+ )

che rappresenta un tratto a pendenza positiva traslato rispetto all’origine.

(56)

50

Questo mostra anche che al crescere della tensione di ingresso V il sistema si comporta come un resistore passivo.

Sostituendo = , = si ottiene: = [ + (1 + )] ( + ) Che diventa = +

quando il guadagno ad anello aperto è molto grande,al limite infinito.

La caratteristica del Diodo di Chua utilizzato nell’esperimento è invece costituita da cinque tratti.

(57)

51

U1 R1 R2 R3 V I U2 R4 R5 R6

Figura 2-0-7 Diodo di Chua a cinque tratti

La caratteristica complessiva è semplicemente la somma delle singole caratteristiche dal momento che entrambi i dispositivi sono controllati in tensione e quindi, essendo collegati in parallelo, le loro correnti si sommano algebricamente.

(58)

52

Le pendenze dei tratti della caratteristica del dispositivo sono date dalle seguenti relazioni:

= − 1 − 1

= − 1 + 1 mentre i punti di breakpoint sono dati da:

=

+ =

+

Il circuito di Chua realizzato per le prove sperimentali è quello mostrato in figura 2-11. Come già accennato prima, questo circuito si basa sulla versione messa a punto da Kennedy molto utilizzata a causa della sua facile realizzazione, basso costo dei componenti, robustezza, ripetibilità.

Sulla sinistra della figura si può notare l’induttore, mentre a destra il diodo di Chua.

(59)

53

Figura 2-0-9 Oscillatore di Chua completo (versione di Kennedy).

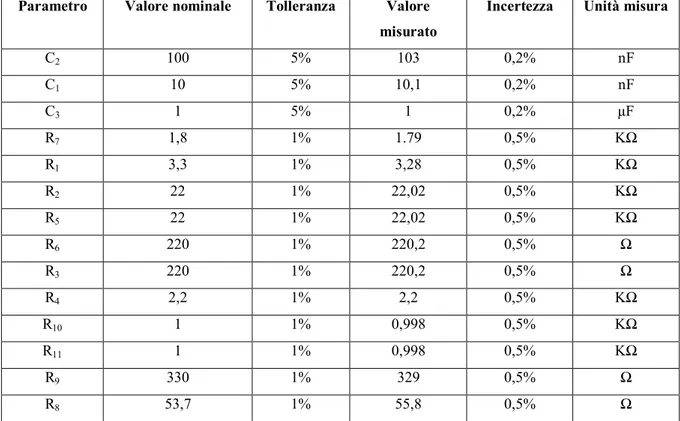
Riportiamo una tabella con i valori dei componenti utilizzati nella realizzazione del circuito sperimentale di figura 2-9

Parametro Valore nominale Tolleranza Valore

misurato

Incertezza Unità misura

C2 100 5% 103 0,2% nF C1 10 5% 10,1 0,2% nF C3 1 5% 1 0,2% µF R7 1,8 1% 1.79 0,5% KΩ R1 3,3 1% 3,28 0,5% KΩ R2 22 1% 22,02 0,5% KΩ R5 22 1% 22,02 0,5% KΩ R6 220 1% 220,2 0,5% Ω R3 220 1% 220,2 0,5% Ω R4 2,2 1% 2,2 0,5% KΩ R10 1 1% 0,998 0,5% KΩ R11 1 1% 0,998 0,5% KΩ R9 330 1% 329 0,5% Ω R8 53,7 1% 55,8 0,5% Ω

(60)

54

2.2 Filosofia del setup sperimentale

Il setup sperimentale [6] è stato pensato e realizzato al fine di permettere lo studio della sincronizzazione di:

 un set di 8 circuiti di Chua collegati tra loro in maniera differente da un punto di vista dei link (adinamici) e della topologia.

 un set di 4 circuiti di Chua collegati tra loro tramite link dinamici in configurazione “all-to-all”.

In questo elaborato di tesi, il setup è costituito da:

 Un set di N circuiti di Chua quasi identici (in questo caso sono stati analizzati il caso N=4 con accoppiamento effettuato tramite link dinamici, e il caso N=8 con accoppiamento effettuato tramite link adinamici resistivi, ma è possibile estendere entrambe le analisi a 16, 32, 64 e così via) i quali costituiscono i “sottosistemi nodi”;

 Una rete per l’implementazione dei link tra i sottosistemi, costituita da un sistema di interruttori allo stato solido, pilotato via USB, e di resistori fissi;

 Un sistema di acquisizione e salvataggio dati multi-channel.

Il setup sperimentale è stato progettato con la prospettiva di aumentare progressivamente il numero dei nodi e quindi, poiché si va ad analizzare un alto numero di diverse topologie, risulta vantaggioso automatizzare le procedure di misura. Allo scopo si è realizzato uno specifico sistema di acquisizione, unito ad un software di controllo sviluppato in ambiente LabView.

(61)

55

La sezione di acquisizione del software consente sia la visualizzazione delle singole variabili nel tempo e dei grafici XY, sia il calcolo in real-time dell’indice di sincronizzazione.

La sezione di controllo, invece, consente di:

 Settare il valore resistivo dell’accoppiamento tra i diversi nodi;  Salvare i dati (grafici e numerici) di uno stato impostato e/o di tutti

gli stati ottenibili variando il valore dei link da 116Ω a 6370Ω in 256 step ( è possibile traslare il range tramite l’ inserimento di un offset).

Figura 2-0-10 Schema a blocchi del setup realizzato.

2.2.1 La rete di interconnessione

La rete di interconnessione realizzata in laboratorio è un circuito in grado di realizzare 32 resistori variabili pilotati via USB.

(62)

56

Dati N circuiti di Chua, sono necessari al più N(N-1)/2 collegamenti per implementare le diverse topologie e studiarne quindi la sincronizzazione.

La rete di interconnessione realizzata è costituita da 4 moduli distinti, ognuno comprendente 8 resistori variabili.

Il componente fondamentale che ha permesso il controllo via software della rete di interconnessione è il modulo USB UM245R di cui parleremo fra poco. Esso fornisce 8 bit utilizzabili come ingresso/uscita. Per come è stato concepito il circuito, 3 degli 8 bit disponibili sono necessari al trasferimento dati per settare il valore di resistenza richiesto, dunque ne restano 5 per l’indirizzamento per un totale di 32 indirizzi indipendenti. Con il circuito di resistori variabili realizzato è possibile quindi settare 32 valori distinti per i link disponibili, sfruttando a pieno le risorse del modulo utilizzato. Il setup resta tuttavia ancora espandibile in quanto è possibile realizzare e pilotare ulteriori link, aggiungendo ulteriori moduli di controllo USB, in vista di un aumento dei nodi e quindi delle topologie da osservare.

Per comprendere a pieno il funzionamento del circuito nel seguente paragrafo sarà descritto inizialmente il funzionamento di una singolo modulo di link resistivi, preoccupandoci solo successivamente dell’interfacciamento tra quest’ultimi e del loro funzionamento contemporaneo.

(63)

57

Figura 2-0-11 Singolo modulo resistivo controllato via USB.

Da un punto di vista hardware, il setup è composto dalle seguenti parti:

 1 modulo UM245R

 4 integrato a porta logica SN74HCT00N [15]  4 Decoder SN74HC138 [16]

 32 Shift-Register SN74HC595N [17]  64 Switch DG412DJZ [18]

 256 resistori

Ciascun resistore variabile è composto dalla serie di 8 resistenze ( di valori

nominali pari a 25, 50, 100, 200, 400, 800, 1600, 3200 [Ω] ), ognuna controllata

da un interruttore, il quale nella fase di “chiusura” non fa altro che shuntarla tramite cortocircuito.

Per ottenere un resistore variabile abbiamo bisogno di due integrati DG412DJZ (64 in totale per realizzare i 32 link suddivisi sulle 4 schede), in quanto ognuno di essi è composto di 4 interruttori.