appunti ed esercizi

(1)

LEZIONI ED ESERCITAZIONI DI

MATEMATICA

Prof. Francesco Marchi

1 Appunti ed esercizi su:

derivate, grafici e studio di funzione

6 dicembre 2010

1_{Per altri materiali didattici o per informazioni:}

Blog personale: http://francescomarchi.wordpress.com/

Indirizzo email: fra.marchi@yahoo.it

http://francescomarchi.wordpress.com

(2)

Indice

1 Derivate 3

1.1 Esercizi di carattere teorico . . . 4

1.1.1 Vero o falso . . . 4

1.2 Relazione tra aspetti grafici ed analitici . . . 5

1.2.1 Date alcune condizioni, individuare il grafico . . . 5

1.2.2 Date alcune condizioni, inventare un grafico plausibile . . 8

1.2.3 Dato il grafico, trarre conclusioni su derivata prima, sec-onda etc . . . 11

1.2.4 Dato il grafico, individuare/scegliere un’espressione ana-litica plausibile per f0 . . . 13

1.2.5 Dato il grafico, determinare il segno della funzione, della derivata prima e seconda in un punto . . . 13

1.2.6 Dato il grafico, determinare il segno di derivata prima e seconda in un intervallo . . . 13

1.2.7 Dato il grafico della funzione, determinare il grafico della derivata . . . 15

Elenco delle tabelle

1.1 Relazione tra il segno delle derivate in un dato punto intervallo e l’andamento della funzione in tale intervallo.. . . 4

1.2 Relazione tra il segno delle derivate in un dato punto x0 e la tipologia di punto. . . 6

1.3 Relazione tra grafico di una funzione e caratteristiche della sua derivata (simili considerazioni possono essere applicate se la fun-zione, anzich´e crescere, cala). . . 7

1.4 Relazione tra punti di interesse particolare per funzione, derivata prima, derivata seconda. . . 7

1

http://francescomarchi.wordpress.com

(3)

2 ELENCO DELLE TABELLE

1.5 Tabella relativa all’esercizio 1 della sezione 1.2.5 (vedi grafico 1.7(a).) . . . 15

http://francescomarchi.wordpress.com

(4)

Capitolo 1

Derivate

Richiami di teoria

Segno delle derivate e grafico della funzione

Segno delle derivate in un intervallo

La relazione tra il segno delle derivate e l’andamento di una funzione in un intervallo, `e sintetizzata nella figura1.1e nella tabella1.1.

Segno delle derivate in un punto e punti notevoli

La relazione tra il segno delle derivate e la tipologia di punto, `e sintetizzata nella figura 1.2e nella tabella1.2.

Relazioni tra aspetti analitici e grafici: approfondimenti

E’ possibile analizzare in maggior dettaglio le relazioni che sussistono tra fun-zione, derivata prima e seconda e grafico della funzione.

La relazione tra funzione e derivata `e sintetizzata nella tabella1.3.

La relazione tra i punti di particolare interesse per la funzione e le sue derivate (prima e seconda) `e sintetizzata in tabella1.4.

3

http://francescomarchi.wordpress.com

(5)

4 CAPITOLO 1. DERIVATE

Tabella 1.1: Relazione tra il segno delle derivate in un dato punto intervallo e l’andamento della funzione in tale intervallo.

sgn f0(x) sgn f00(x) monoton`ıa concavit`a grafico

+

+ crescente verso l’alto 1.1(a)

0 crescente nulla (retta) 1.1(b)

− crescente verso il basso 1.1(c)

0 0 costante nulla (retta) 1.1(d)

-+ decrescente verso l’alto 1.1(e)

0 decrescente nulla (retta) 1.1(f)

− decrescente verso il basso 1.1(g)

1.1 Esercizi di carattere teorico

1.1.1 Vero o falso

Stabilire se le seguenti affermazioni sono vere o false.

Nel caso in cui un’affermazione sia falsa, provarlo con un controesempio. 1. Se in un punto x = x0 una funzione `e continua, allora sar`a derivabile in

quel punto.

2. Se in un punto x = x0 una funzione non `e derivabile, allora non sar`a

continua in quel punto.

3. Per una certa funzione, risulta che f0(x1) > f 0

(x2). Allora in x = x1 la

funzione varr`a pi`u che in x = x2.

4. Il fatto che la derivata prima di una funzione sia positiva in un certo punto non implica che la funzione sia positiva in quel punto.

5. Il grafico della derivata f0 di una certa funzione f `e una retta orizzon-tale nell’intervallo [3, 7]. Allora la funzione f `e una retta obliqua in tale intervallo.

6. Il grafico della derivata f0 di una certa funzione f `e una retta obliqua nell’intervallo [3, 7]. Allora la funzione f `e una retta orizzontale in tale intervallo.

http://francescomarchi.wordpress.com

(6)

1.2. RELAZIONE TRA ASPETTI GRAFICI ED ANALITICI 5

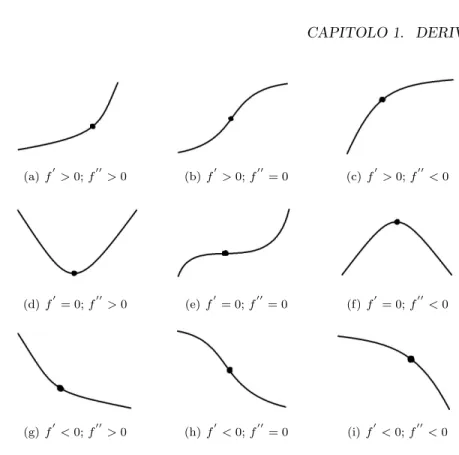
(a) f0> 0; f00> 0 (b) f0 > 0; f00= 0 (c) f0> 0; f00< 0

(d) f0 = 0; f00= 0

(e) f0 < 0; f00> 0 (f) f0 < 0; f00= 0 (g) f0 < 0; f00< 0

Figura 1.1: Comportamento di una funzione in un dato punto.

1.2 Relazione tra aspetti grafici ed analitici

1.2.1 Date alcune condizioni, individuare il grafico

Nota: I seguenti esercizi vanno svolti procedendo “per esclusione”, ovvero come segue:

• Si considera il primo grafico e si controllano, relativamente ad esso, le varie condizioni

– Condizione 1:

∗ Non vale: si esclude il grafico 1 e si passa al successivo ∗ Vale: si passa alla condizione successiva

– Condizione 2:

∗ Non vale: si esclude il grafico 1 e si passa al successivo ∗ Vale: si passa alla condizione successiva

– . . . per le altre condizioni

• Se il primo grafico soddisfa tutte le condizioni, `e quello corretto; altrimenti si passa al grafico 2 e si ripete la procedura illustrata sopra.

• . . .

http://francescomarchi.wordpress.com

(7)

Tabella 1.2: Relazione tra il segno delle derivate in un dato punto x0e la tipologia di punto.

sgn f0(x0) sgn f 00

(x0) tipo punto grafico

+

+ / 1.2(a)

0 flesso a tangente obliqua ascendente 1.2(b)

− / 1.2(c)

0

+ minimo 1.2(d)

0 flesso a tangente orizz. 1.2(e)

− massimo 1.2(f)

-+ / 1.2(g)

0 flesso a tangente obliqua discendente 1.2(h)

− / 1.2(i)

• Si continuano a scorrere i grafici fino ad individuare quello corretto La procedura appena proposta `e “di tipo algoritmico”; con un po’ di esperienza, `

e possibile applicarla in modo pi`u flessibile.

Esercizio 1

Di una data funzione si sa che:

• f0 < 0 in (3, +∞); • f00 = 0 in x = −3;

• f non `e derivabile in x = 3.

Stabilire quale, fra i grafici in figura1.3, rappresenta tale funzione.

Esercizio 2

Di una data funzione si sa che:

http://francescomarchi.wordpress.com

(8)

Tabella 1.3: Relazione tra grafico di una funzione e caratteristiche della sua derivata (simili considerazioni possono essere applicate se la funzione, anzich´e crescere, cala).

Funzione f Derivata f0

`

e costante vale zero

cresce poco ha valori piccoli

cresce molto ha valori grandi

cresce sempre meno `e positiva, ma calante

cresce di pi`u `e positiva e crescente

`

e una retta obliqua `e una retta orizzontale

cresce verso asintoto orizzontale tende a zero

cresce verso asintoto obliquo tende ad asintoto orizzontale

cresce verticalmente ha asintoto verticale

Tabella 1.4: Relazione tra punti di interesse particolare per funzione, derivata prima, derivata seconda.

Funzione f Derivata f0 Derivata seconda f00

asintoto verticale asintoto verticale asintoto verticale

estremante (min o max) vale zero non zero

flesso obliquo non zero vale zero

cuspide discontinua continua

punto angoloso discontinua discontinua

http://francescomarchi.wordpress.com

(9)

(a) f0> 0; f00> 0 (b) f0> 0; f00= 0 (c) f0> 0; f00< 0

(d) f0= 0; f00> 0 (e) f0 = 0; f00= 0 (f) f0 = 0; f00< 0

(g) f0< 0; f00> 0 (h) f0< 0; f00= 0 (i) f0< 0; f00< 0

Figura 1.2: Comportamento di una funzione in un dato punto.

• f00 > 0 in (−∞, 1) e f00< 0 in (1, 2); • f0 `e discontinua in x = 4;

• f0(x) = 1 in (4, +∞).

Stabilire quale, fra i grafici in figura1.4, rappresenta tale funzione.

1.2.2 Date alcune condizioni, inventare un grafico

plausi-bile

Esercizio 1

Rappresentare graficamente funzioni che soddisfino le condizioni seguenti:

• f sia positiva in x = 4 e abbia in tale punto la derivata prima positiva e la derivata seconda negativa;

• f0 sia negativa in (−∞, −4) e positiva in (−4, +∞) ed inoltre valga f (5) < f (−6)

http://francescomarchi.wordpress.com

(10)

(a)

(b)

(c)

(d)

Figura 1.3: Grafici relativi all’esercizio1.2.1.

http://francescomarchi.wordpress.com

(11)

(a)

(b)

(c)

(d)

Figura 1.4: Grafici relativi all’esercizio1.2.1.

http://francescomarchi.wordpress.com

(12)

1.2.3 Dato il grafico, trarre conclusioni su derivata prima,

seconda etc

Esercizio 1

Facendo riferimento al grafico rappresentato in 1.5(a), stabilire se le seguenti affermazioni sono vere o false:

1. Nel punto x = A la funzione ha derivata prima positiva.

2. Nel punto x = A la derivata prima `e crescente.

3. Nell’intervallo [B, C] la funzione ha derivata seconda positiva.

Esercizio 2

Facendo riferimento al grafico rappresentato in 1.5(b), stabilire se le seguenti affermazioni sono vere o false:

1. f0(0) < 0;

2. f00(x) > 0 in (B, +∞);

3. f0(A) < f0(C);

4. x = B `e un punto di non derivabilit`a;

5. x = B `e un punto di cuspide;

6. Il grafico di f0 sar`a discontinuo in x = B.

Esercizio 3

Facendo riferimento al grafico rappresentato in 1.5(c), stabilire se le seguenti affermazioni sono vere o false:

1. Il grafico di f0(x) sar`a una retta orizzontale in (A, B);

2. f0(x) = 0 in (A, B); 3. f0(x) = 0 in (B, +∞); 4. f00(x) < 0 in (0, A); 5. x = 0 `e un punto angoloso.

http://francescomarchi.wordpress.com

(13)

(a) Grafico relativo all’esercizio 1 della sezione1.2.3.

(b) Grafico relativo all’esercizio 2 della sezione1.2.3.

(c) Grafico relativo all’esercizio 3 della sezione1.2.3.

Figura 1.5: Grafici relativi agli esercizi della sezione1.2.

http://francescomarchi.wordpress.com

(14)

1.2.4 Dato il grafico, individuare/scegliere un’espressione

analitica plausibile per f

0

Esercizio 1

Una data funzione ha il grafico rappresentato in figura1.6. Stabilire quale fra le seguenti `e un’espressione plausibile per la derivata di tale funzione:

f0(x) = x2(3 ln x + 1) (1.1)

f0(x) = 5 − ln x (1.2)

f0(x) = 2 + x − 3x2 (1.3)

Figura 1.6: Grafico relativo all’esercizio 1 della sezione1.2.4.

1.2.5 Dato il grafico, determinare il segno della funzione,

della derivata prima e seconda in un punto

Esercizio 1

Si consideri il grafico di funzione riportato in figura1.7(a). Completare la tabella

1.5relativa a tale funzione.

1.2.6 Dato il grafico, determinare il segno di derivata

pri-ma e seconda in un intervallo

Esercizio 1

Si considerino le figure riportate nel grafico 1.9. Segnare su di essi dei punti ritenuti significativi, indicandoli con x1, x2 e cos`ı via, e determinare:

http://francescomarchi.wordpress.com

(15)

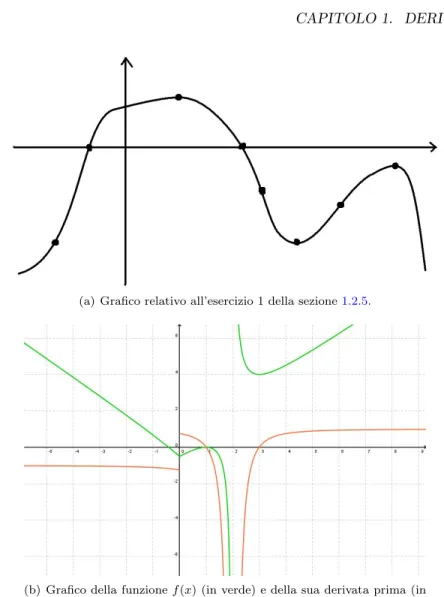
(a) Grafico relativo all’esercizio 1 della sezione1.2.5.

(b) Grafico della funzione f (x) (in verde) e della sua derivata prima (in arancione).

(c) Grafico della funzione f (x) (in verde) e della sua derivata seconda (in arancione).

Figura 1.7: Grafici relativi all’esempio svolto1.2.7.

http://francescomarchi.wordpress.com

(16)

Tabella 1.5: Tabella relativa all’esercizio 1 della sezione1.2.5(vedi grafico1.7(a).)

sgn f sgn f0 sgn f00 tipo punto x1 x2 x3 x4 x5 x6 x7 x8

• il segno della derivata prima; • il segno della derivata seconda;

• le coordinate dei massimi e dei minimi; • le coordinate dei punti di flesso; • i punti di non derivabilit`a.

1.2.7 Dato il grafico della funzione, determinare il grafico

della derivata

Esempio svolto

Consideriamo la funzione rappresentata in figura1.8(a).

Nelle figure successive sono rappresentate la funzione insieme con la sua derivata prima1.8(b)e la funzione insieme con la sua derivata seconda1.8(c). Vediamo adesso come `e possibile costruire tali grafici con ragionamenti di tipo qualitativo.

• Grafico della derivata prima

http://francescomarchi.wordpress.com

(17)

– in (−∞, 0) f decresce in modo (quasi) costante (`e all’incirca una retta); perci`o f0 ha un valore costante, negativo, pari al coefficiente angolare di tale retta;

– in x = 0 la funzione comincia a crescere, per cui passeremo brus-camente da una situazione di derivata negativa ad una di derivata positiva; in altre parole, al punto angoloso x = 0 corrisponde una discontinuit`a nel grafico della derivata prima;

– in (0, 1) la funzione cresce sempre meno, per cui la derivata è positiva (perché la funzione cresce), ma sempre più piccola (perché cresce sempre meno);

– in x = 0 la funzione ha un massimo relativo e la derivata vale zero; – in [0, 2] la funzione decresce (per cui la derivata sar`a negativa) sempre

più rapidamente (per cui f0 assumerà valori sempre più negativi); – in x = 2 sia f che f0 hanno un asintoto verticale;

– in [2, 3] la funzione decresce (⇒ f0 < 0) sempre meno (per cui la derivata assume valori sempre meno negativi);

– in x = 3, f ha un minimo e la derivata vale zero;

– in [3, +∞) la funzione cresce, per cui la derivata `e positiva; in parti-colare f tende ad un asintoto obliquo, per cui la sua derivata tender`a ad un asintoto orizzontale.

• Grafico della derivata seconda

– in (−∞, 2), f volge la concavità verso il basso, per cui la derivata seconda è negativa in tale intervallo; inoltre, visto che la derivata prima è all’incirca costante fino a x = −1 circa, la derivata seconda (che è la sua derivata) varrà circa zero;

– in x = 2, f00(x) ha un asintoto verticale, cos`ı come f e f0;

– in [2, +∞), f volge la concavit`a verso l’alto, per cui f00 > 0; in particolare tende a zero, con considerazioni simili a quelle fatte in precedenza.

Esercizio 1

Stesso esercizio dell’esempio svolto, in relazione ai grafici riportati in figura1.9.