Studio di alcuni problemi di topologia nella teoria di gauge in QCD

In QCD il ruolo della topologia `e centrale. La topologia `e strettamente legata al continuo, dato che dal punto di vista matematico non pu`o essere definita sul discreto. Ma `e proprio a causa del suo carattere non perturbativo che lo strumento pi`u adatto a misurare grandezze ad essa associate risulta essere il reticolo.

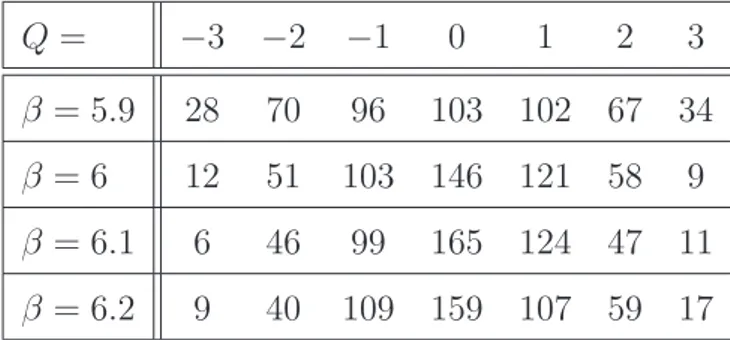
Per ottenere risultati fisici dalle misure fatte su reticolo `e necessario rinor-malizzare. Per quanto riguarda la densit`a di carica topologica Q(x), poich´e la divergenza della corrente ad essa associata su reticolo non `e zero, si avr`a la comparsa di un coefficiente moltiplicativo Z. La rinormalizzazione della suscettivit`a topologica

χ = Z

d4_x ­_{0 | T (Q(x)Q(0) | 0}®

richieder`a un fattore moltiplicativo Z2<sub>, dovuto alla presenza di due operatori</sub> Q, e di un termine additivo M, dovuto alla singolarit`a del prodotto Q(x)Q(0) quando x → 0. In formula DQ2 r V E = Z(β)2_a4_{χ + M(β),}

dove Qr`e la carica misurata su reticolo, a `e il passo reticolare e β `e la costante

di accoppiameno di gauge. Questa relazione consente di ricavare Z e M se si dispone di configurazioni di gauge su reticolo di cui sia nota la carica.

Per fare ci`o, delle configurazioni classiche a carica nulla o a carica 1 vengono termalizzate, facendo affidamento sul fatto che la componente infrarossa della configurazione rimanga in buona misura immutata durante questo processo. La carica viene comunque monitorata durante la termalizzazione utilizzando il metodo di cooling. Poich´e anche questa tecnica `e basata sulle stesse ipotesi che fanno presupporre che la carica rimanga presente durante il processo di termalizzazione, `e chiaro che siamo in presenta di una sorta di tautologia. Anche se per questo metodo esistono molte prove di consistenza, il problema della coerenza rimane.

Con l’introduzione dei fermioni di Ginsparg-Wilson `e divenuto possibile utilizzare il teorema di Atiyah-Singer per misurare la carica di una confi-gurazione su reticolo tramite tecniche di analisi spettrale. Pur essendo an-che queste ultime affette da alcuni errori sistematici, esse rappresentano un metodo che non fa uso del cooling per misurare la carica.

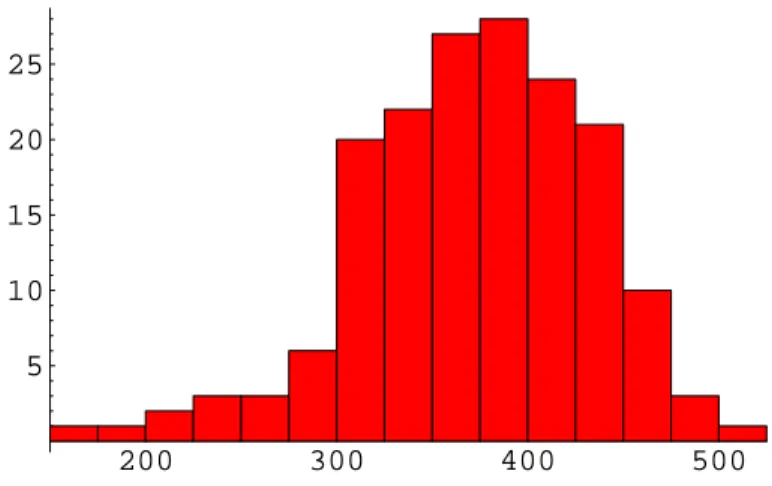
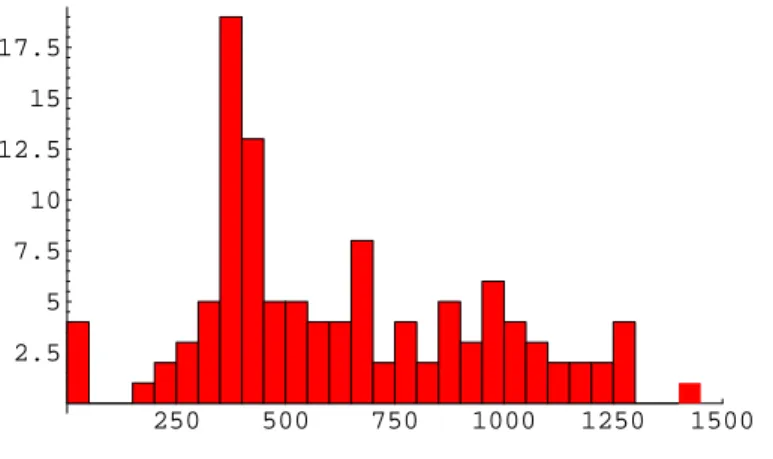
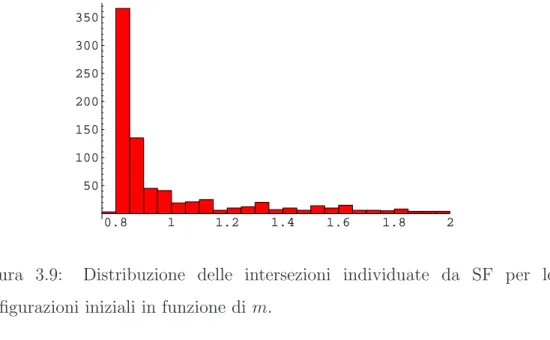
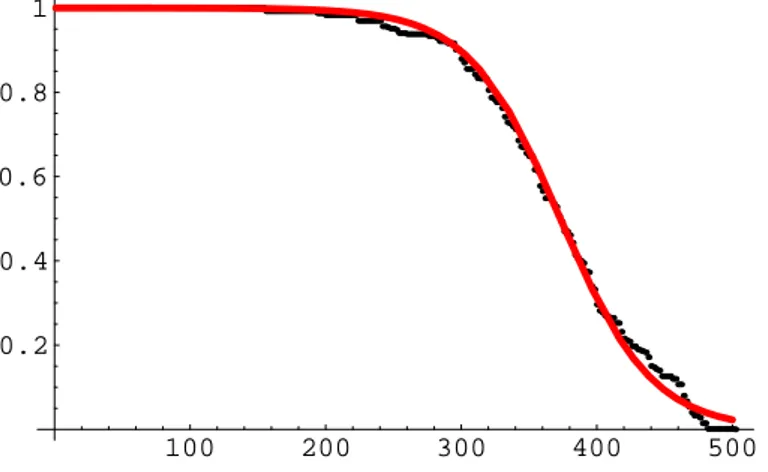
Grazie a questo fatto `e stato possibile fare un confronto [7] fra il metodo che utilizza tecniche di heating e di cooling per determinare Z e M con il metodo che invece sfrutta le propriet`a dei fermioni di Ginsparg-Wilson. `E risultato che le due tecniche sono in accordo nei limiti dell’errore statistico (3% − 4%). Ne risulta che il metodo di cooling ha buoni fondamenti teorici. Inoltre la sua semplicit`a e velocit`a lo rendono preferibile ai metodi di analisi spettrale. Risulta perci`o importante studiare l’errore commesso nella deter-minazione della carica topologica utilizzando l’ipotesi alla base dei metodi di cooling e di heating. In altre parole vogliamo quantificare l’errore sistematico commesso sulla misurazione della carica dopo n passi di cooling o di heating. In questa tesi, dopo aver introdotto la teoria di QCD (capitolo 1), si passa a presentare il ruolo della carica topologica (capitolo 2). Per analizzare quan-titativamente il metodo di cooling, utilizziamo il metodo “Spectral Flow” per

ricavare quando scompare la carica topologica dalle configurazioni di gauge in SU(3) contenenti un istantone o un antiistantone, dopo aver eseguito su di esse un certo numero di passi di raffreddamento. Si `e cos`ı ottenuta una statistica che lega il numero di passi di cooling alla presenza di un istantone nella configurazione di gauge (capitolo 3). Inoltre si `e misurata la lunghezza di autocorrelazione della carica topologica su configurazioni legate fra loro da un passo di update.

Istantoni e problemi connessi

Nel primo paragrafo si introduce la lagrangiana di QCD, definendo i campi di gauge e le trasformazioni associate. Si introducono poi i funzionali gene-ratori delle funzioni di Green e si passa nello spazio euclideo. Nel secondo paragrafo si discutono gli aspetti legati alla rinormalizzazione, fra cui anche la libert`a asintotica. Nel terzo paragrafo si tratta della simmetria chirale, con particolare riferimento all’anomalia della corrente assiale di singoletto. Nel quarto paragrafo si illustra il problema U(1), si definiscono gli istantoni e si studiano le interconnessioni fra i due argomenti. Nel quinto paragrafo si introducono i modi zero fermionici e si ricava il teorema di Atiyah-Singer, fondamentale per il metodo dello spectral flow. Nel sesto paragrafo, infine, si considerano i dipoli di Goldstone e se ne studia il ruolo nella risoluzione del problema U(1).

1.1

Lagrangiana di QCD

Nei primi anni sessanta si not`o che lo spettro adronico `e ben classifica-bile usando le rappresentazioni irriducibili di SU(3), tuttavia la

tazione fondamentale di questo gruppo non era osservata. Si avanz`o allora l’ipotesi che tutti gli adroni fossero composti da particelle (quark) a spin 1/2 che trasformano come la rappresentazione fondamentale di SU(3). La lagrangiana associata al modello a quark liberi `e

L(x) = Nf X k=1 ¯ ψk(i∂µγµ− mk) ψk,

con Nf il numero di flavours e mk la massa associata alla particolare specie.

I problemi legati ai barioni ∆++_{, ∆}−_{, Ω}− _{fecero nascere l’esigenza di}

introdurre un nuovo numero quantico: il colore. Grazie ad esso `e possibile mantenere l’ipotesi che il momento angolare orbitale dei quark nei barioni sia nullo senza violare il principio di Pauli. `E sufficiente allora aggiungere ai campi un nuovo indice che tenga conto del colore. Successivamente la simmetria globale SU(3) di colore venne tramutata in simmetria di gauge locale, ottenendo cos`ı la lagrangiana di QCD.

Dato il campo di gauge

Aµ = 8 X a=1 Aa µ λa 2 , dove Aa

µ sono i campi gluonici e λa sono le matrici di Gell-Mann che

soddi-sfano le seguenti relazioni di commutazione di SU (3) [λa_{, λ}b_{] = i f}abc λc

2 , tr (λ

a_λb_{) = δ}ab_,

in cui fabc _{sono le costanti di struttura del gruppo di gauge, la lagrangiana}

di QCD `e LQCD = − 1 4tr GµνG µν₊ Nf X k=1 ¯ ψk(iνµDµ− mk) ψk, (1.1) con Gµν = ∂µAν − ∂νAµ − i g [Aµ, Aν],

Dµψk = (∂µ − i g Aµ) ψk.

La costante g `e detta costante di accoppiamento nuda. La lagrangiana (1.1) `e invariante sotto trasformazione di gauge

Ω(x) = e−i Θa(x) λa, (1.2) ¯ ψk(x) → Ω(x) ¯ψk(x), ψk(x) → Ω(x) ψk(x), Aµ(x) → Ω(x)Aµ(x)Ω+(x) − i g (∂µΩ(x)) Ω +_{(x) . (1.3)} Il termine −1

2tr GµνGµν `e quello cinetico associato ai campi gluonici.

Il valore medio di aspettazione sul vuoto di un operatore O¡A, ψ, ¯ψ¢ si esprime usando il formalismo di Feynman

D 0 | O | 0 E = 1 Z Z dA dψ d ¯ψ O¡A, ψ, ¯ψ¢eiS(A,ψ, ¯ψ), (1.4) con Z = Z dA dψ d ¯ψ eiS(A,ψ, ¯ψ)_,

in cui gli integrali sui campi sono di tipo funzionale. `E necessario fissare una gauge per evitare divergenze in (1.4)

Fa(A) = 0, a = 1, . . . , 8,

e aggiungere un termine di gauge fixing del tipo λ

2Fa[A]Fa[A] alla lagrangiana, in cui Fa[A] `e un funzionale dei campi gluonici che trasforma come un ottetto

di SU(3) di colore. Al fine di mantenere l’invarianza di gauge, si segue il metodo definito da Fadeev-Popov e si utilizza nell’integrale l’identit`a

1 = ∆(A) Z

dθ eiλ/2Fa2(Aθ),

dove Aθ _{`e il valore di A dopo una trasformazione di gauge (1.3). Otteniamo}

quindi per (1.4) D 0 | O | 0E= 1 Z Z dA dψ d ¯ψ dω d¯ω O eiS(A,ψ, ¯ψ,ω,¯ω) _(1.5)

con

Z = Z

dA dψ d ¯ψ dω d¯ω eiS(A,ψ, ¯ψ,ω,¯ω),

dove ω e ¯ω sono i ghost di Fadeev-Popov. L’azione in (1.5) `e quella completa di QCD.

Le funzioni di Green generiche possono essere cos`ı definite come prodotti T-ordinati di stringhe di campi e ghost

D 0 | T³ Y ijklm ω(xi) ¯ω(yk) ψ(zj) ¯ψ(tl)Amµm(p) ´ | 0 E . Il funzionale generatore Z(J) associato alle funzioni di Green `e

Z(J) = Z

dA dψ d ¯ψ dω d¯ω eiS(A,ψ, ¯ψ,ω,¯ω)+iJω+i¯ωJω+iJψ+i ¯ψJψ+iJµAµ_,

in cui sono sottintesi gli indici di colore e di flavour e anche l’integrazione sulle coordinate. Per ottenere solo le funzioni di Green connesse, si utilizza il funzionale W (J) definito da

Z(J) = eiW (J), che soddisfa la relazione

G(n)(x1, . . . , xn) = h−i n W δn_W δJ(x1) ...δJ(xn) ¯ ¯ ¯ J=0 i .

Volendo invece ottenere il generatore dei soli grafi ad albero connessi, dovremmo definire i campi classici

ηi(x) =

δW (J) δJi(x)

, (1.6)

in cui i `e un indice che varia su tutti i campi accoppiati con la sorgente omologa. Se la (1.6) `e invertibile, possiamo operare la seguente trasformata di Legendre

Lef f(η) = W (J) −

X

i

Il funzionale Lef f(η), detto lagrangiana effettiva di QCD, `e il generatore delle

funzioni di Green connesse, irriducibili a una particella.

Il passaggio dallo spazio minkowskiano a quello euclideo mette in luce le analogie con la meccanica statistica e consente di studiare le propriet`a del vuoto della teoria. Si effettua quindi la trasformazione

  

x(m)_i = x(e)_i , ∂_i(m) = −∂_i(e), x(m)₀ = −i x(e)₄ , ∂₀(m) = i ∂₄(e),

dove m ed e stanno a indicare rispettivamente l’appartenenza allo spazio minkowskiano e euclideo. Avendo reso immaginaria la parte x0 di xµ,

dob-biamo operare allo stesso modo anche su A0. Complessivamente A(e)µ `e cos`ı

definito 

 

A(m)_i = −A(e)_i

A(m)₀ = i A(e)₄ . (1.7)

Le definizioni di x(e)µ e A(e)µ differiscono per un fattore -1. In tal modo

   D(m)_i = −D_i(e) D(m)₀ = i D₄(e). (1.8) Da (1.7) e (1.8) otteniamo per Gµν    G(m)_ij = G(e)_ij G(m)_0j = −i G(e)_4j .

Passiamo alla definizione dei campi ψ. Per quanto riguarda le matrici γµ

abbiamo 

 

γ_i(m) = i γ_i(e) γ₀(m) = γ₄(e) , da cui {γµ(e), γ(e)ν } = 2 δµν, e per i campi ψ e ¯ψ

   ψ(m) _{= ψ}(e) ¯ ψ(m) _{= i ¯ψ}(e)_.

Abbiamo quindi per l’azione euclidea        S(m) ₌ Z d4x(m) h − 1 4G (m) µν G(m)µν + ¯ψ(m)(i γµ(m)Dµ(m) − M) ψ(m) i S(e) ₌ Z d4_x(e)_[−1 4G (e)

µνG(e)µν + ¯ψ(e)(i γµ(e)D(e)µ − M) ψ(e)] ,

(1.9) dove M `e la matrice di massa, e per la funzione W(e)

W(e) = Z

[dA d ¯ψ dψ] e−S(e)[Aµ, ¯ψ, ψ] . _(1.10)

La trasformazione sopra descritta, che porta i tempi reali in immaginari `e detta rotazione di Wick e, come abbiamo visto, trasforma l’azione nel modo seguente

i S(m) → −S(e).

Il vantaggio di questa trasformazione consiste nel poter trascurare configu-razioni con azione classica infinita nell’approssimazione semiclassica WKB.

Poich´e il formalismo euclideo `e la continuazione analitica di quello minkow-skiano, d’ora in poi eviteremo di appesantire la notazione e non specifi-cheremo pi`u l’indice e.

Nel seguito ci servir`a calcolare il valore di aspettazione di un operatore O dipendente solo dai campi gluonici. Svolgendo l’integrazione sui campi fermionici, dalla (1.4) otteniamo

D 0 | O | 0 E = R dA O¡A¢eiSef f(A) R dA eiSef f(A) , dove

Sef f(A) = SG(A) − ln det K(A),

SG(A) `e la parte strettamente gluonica dell’azione euclidea in (1.9) e K(A)

`e la matrice nello spazio-tempo e nello spazio di Dirac Kx,α,y,β(A) = h i γν(Aν + ∂ν) + M i α,βδ (4)_{(x − y). (1.11)}

1.2

Rinormalizzazione in QCD

Ogni volta che in una teoria compaiono delle quantit`a divergenti, esse van-no regolarizzate tramite un qualche parametro di cut-off, che pu`o essere ad esempio il “passo reticolare”, o una costante ² dimensionale. Queste quantit`a, essendo introdotte artificialmente, devono poi sparire per avere una teoria coerente. Il processo adottato per ottenere questo risultato si chiama rinor-malizzazione. In uno schema di rinormalizzazione, le quantit`a calcolate in presenza di coefficienti di regolarizzazione sono quantit`a non fisiche, legate alle quantit`a fisiche da costanti di rinormalizzazione che dipendono dagli stessi coefficienti e sono dette nude, come gi`a la costante di accoppiamento g.

In particolare mostriamo questo processo di rinormalizzazione per la QCD utilizzando il metodo di regolarizzazione dimensionale che consiste nel fare la seguente sostituzione Z d4_p 2π4 → ν ² 0 Z d4−²_p 2π4−²,

in cui ² ∈ R+_{. Diminuendo il volume sul quale si integra, si elimina la} diver-genza. La quantit`a ν0 viene introdotta per correggere le dimensioni. Inoltre viene estesa l’algebra delle matrici γ ad uno spazio con 4 − ² dimensioni.

Come si `e detto, il parametro ² deve essere mandato a 0 per riottenere il mondo reale. In questo limite ricompaiono le divergenze nella forma

N(²) = 2

² − γE + ln(4π),

dove γE`e la costante di Eulero. Seguendo lo schema della rinormalizzazione si

introducono le seguenti costanti di rinormalizzazione che legano le quantit`a non rinormalizzate a quelle rinormalizzate in modo che quest’ultime siano regolari

Aa µR = Z −1/2 A AaµN R, λR= ZλλN R, ωiR = Zω−1/2ωiN R, gR= Zg−1gN R, (1.12) miR = Zim iN R−1 ,

dove λ `e inteso come il parametro di gauge fixing e le Z dei campi fermionici e dei loro coniugati sono considerate uguali. Le quantit`a Z risultano funzioni del parametro ². Quindi per fare in modo che le quantit`a rinormalizzate siano regolari, le Z devono essere divergenti per ² che tende a zero.

Esistono vari schemi di rinormalizzazione differenti, che corrispondono a strade diverse per sottrarre le divergenze alle funzioni di Green. Ad esem-pio, nello schema µ si fissano delle funzioni di Green indipendenti in nu-mero uguale alle Z indipendenti, calcolate per particolari valori degli impulsi esterni e quindi si ricavano tutte le costanti di rinormalizzazione indipendenti.

`

E naturale richiedere che la scelta di un differente schema di rinorma-lizzazione o, all’interno di uno stesso schema, di differenti parametri (come gli impulsi nello schema µ), non influenzi la determinazione delle quantit`a fisiche. Si definisce gruppo di rinormalizzazione l’insieme delle trasformazioni che cambiano i parametri fissati all’interno di ogni schema.

Se, ad esempio, prendiamo in considerazione la costante di accoppiamento g al valore ν, abbiamo dalla (1.12)

gN R = Zg(ν)gR(ν),

mentre ad un valore ν0 _{diverso da ν abbiamo}

e quindi

gR(ν0) = Zg(ν0)Zg−1(ν0)gR(ν) = Zg0(ν0, ν)gR(ν).

La funzione Z0

g permette di passare da una scala all’altra ed `e quindi continua

per ² che tende a zero.

Per studiare il comportamento delle quantit`a fisiche sotto il gruppo di rinormalizzazione `e utile introdurre le equazioni di Callan-Symanzik, che si ottengono imponendo l’invarianza di quantit`a non rinormalizzate rispet-to alla scala. Considerando ad esempio la funzione di Green G(pi, g, m, λ)

dipendente dagli impulsi esterni pi, si ha

ν d dνGN R(pi, gN R, mN R, λN R) = 0, che d`a ³ ν ∂ ∂ν + gRβ ∂ ∂gR + δλR ∂ ∂λR + X i miγm,i ∂ ∂mi − γG ´ GR = 0, (1.13) in cui GR= GR(pi, gR, mR, λR, ν) = ZG−1GN R(pi, gN R, mN R, λN R, ν),

dove ZG = Π Zk1/2 `e il prodotto delle Z dei campi nella funzione di Green

considerata, e le funzioni β, γ e δ sono definite tramite le equazioni ν d

dν GR(ν) = βgR(ν), ν d

dν mR,i(ν) = γm,imR,i(ν), ν d dν λR(ν) = δλR(ν), Z−1 G ν d dνZG = γG.

Se la funzione di Green presa in esame ha dimensione dG, allora pu`o essere

messa nella forma

GR= νdGF³pi ν, gR, mR ν , λR ´ , (1.14)

con F una funzione adimensionale. Utilizzando la (1.14), si pu`o arrivare all’equazione analoga alla (1.13)

³ ν ∂ ∂ν + gβ ∂ ∂g + δλ ∂ ∂λ + X i miγm,i ∂ ∂mi − γG+ dG ´ GR = 0.

Scalando gli impulsi secondo pi → ρ pi, l’equazione risulta

³ −ρ ∂ ∂ρ + gRβ ∂ ∂gR + δλR ∂ ∂λR +X i mR,i(γm,i−1) ∂ ∂mR,i − γG+dG ´ GR = 0. (1.15) La comparsa nell’equazione dei termini γm,i− 1 `e dovuta al fatto che, a causa

della (1.14), eseguire la trasformazione pi → ρ pi `e equivalente a mandare

ν → ρ−1_{ν e contemporaneamente m}

k → ρ−1mk nella funzione F .

Si definiscono adesso i cosiddetti parametri running ¯g(ρ), ¯m(ρ) e ¯λ(ρ) tramite le equazioni d d ln ρ ¯g(ρ) = ¯g(ρ) β(¯g), d d ln ρm(ρ) = ¯¯ m(ρ) γ( ¯m), d d ln ρλ(ρ) = ¯¯ λ(ρ) δ(¯λ), (1.16)

con le condizioni al contorno

¯g(1) = gR(ν), m(1) = m¯ R(ν), ¯λ(1) = λR(ν).

La soluzione generale della (1.15) `e GR ¡ ρpi, gR(ν), mR(ν), λR(, ν), ν ¢ = ρdG exp h − Z _{ln ρ} 0 d ln ρ0γG ¡ ¯g(ρ0), ¯m(ρ0), ¯λ(ρ0)¢iGR ¡ pi¯g(ρ), ¯m(ρ), ¯λ(ρ), ν ¢ . Conoscendo le espansioni perturbative delle funzioni β, γ e δ, possiamo integrare le (1.16), ottenendo le espressioni per i parametri running. In particolare, per la funzione β si ha

β(¯g) = − ³ β0 α¯s 4π + β1 ³ ¯αs 4π ´₂ + β3³ ¯αs 4π ´₃ + . . . ´ ,

in cui β0, β1 > 0 sono indipendenti dallo schema di regolarizzazione e al primo ordine nell’espansione perturbativa `e [3] (p. 208)

¯

αs(p2) =

2π

ln(p/Λ), dove p = ρ ν e Λ = ν e

−2π/(β0αs(ν))_{. (1.17)}

Poich´e β0 > 0, la costante di accoppiamento dei quark ai gluoni diventa 0 quando l’impulso p → ∞, propriet`a che vale a qualsiasi ordine perturbativo. Si ha quindi che, a piccole distanze o a grandi impulsi trasferiti, i quark si comportano come liberi. Questo fenomeno `e noto come libert`a asintotica.

1.3

La simmetria chirale

Quando mu = md = ms = 0 si ha che [4], date due matrici unitarie U e V

di dimensione 3 × 3, considerando le seguenti trasformazioni per i campi di quark ψ_i+ → Uijψj+, ψi− → Vijψ−j , con ψ (±) j = 1 ± γ5 2 ψi, (1.18) la lagrangiana di QCD `e invariante. Le trasformazioni (1.18), che sono del tipo U(3)L

N

U(3)R, sono associate alla simmetria chirale.

Vogliamo ora scrivere le correnti conservate associate a queste trasfor-mazioni. Definiamo

U(θ) = e−i/2gPaλaθa, V (θ0) = e−i/2g

P

aλaθ0a,

dove λ0 _{= 1 e λ}a _{per a = 1, . . . , 8 sono le matrici di Gell Mann. Si applica il}

teorema di Noether alle (1.18) e si ottengono le quantit`a La (±) = Z d3_{x ¯ψ γ} 0 1 ± γ5 2 λ a_ψ(x),

che derivano dalle correnti conservate J_(±)µ,a= ¯ψ γµ1 ± γ5

2 λ

Ponendo

A(θ) = e−i/2gPaLa+θa, B(θ0) = e−i/2g

P aLa−θ0a, risulta che A(θ)ψ+ i A+(θ) = Uij(θ) ψj+, B(θ0)ψi−B+(θ0) = Vij(θ0) ψ−j , e quindi i La

(±) sono i 9 generatori delle trasformazioni (1.18). Definiamo poi i generatori a parit`a definita

Qa = La₊+ La₋ Qa₅ = La₋+ La₋ (1.20) che verificano le seguenti regole di commutazione

£

Qa, Qb¤= 2ifabcQc, £Qa, Qb₅¤= 2ifabcQc₅, £Qa₅, Qb₅¤= 2ifabcQc. Gli operatori

F₅µ,a = 1 2

¡

J₊µ,a− J₋µ,a¢, (1.21) costruiti a partire dalle correnti (1.19), sono ancora gauge invarianti, a parit`a definita e conservati.

Particolarmente importante `e la corrente assiale di singoletto, detta anche corrente U(1) assiale

j₅µ = 3 X k=1 ¯ ψk(x) γµγ5ψk(x), (1.22)

che `e associata al gruppo di trasformazioni ψk → eiγ5αψk

abeliano e conservata nel limite chirale.

Le correnti (1.21) hanno divergenza nulla nel limite chirale. Se anche la (1.22) avesse lo stesso comportamento, la simmetria assiale di singoletto

potrebbe essere manifesta oppure potrebbe essere rotta spontaneamente. Nel primo caso avremmo che tutti gli adroni massivi comparirebbero in doppietti di parit`a, e questo non accade.

D’altra parte, se ci fosse rottura spontanea, dovremmo osservare un bosone di Goldstone aggiuntivo rispetto ai gi`a noti pioni. Per un teorema dovuto a Weinberg [8] si ha che nel limite non chirale i bosoni acquistano perturbati-vamente massa non nulla e che inoltre valgono le relazioni

m2_a = O(m), a = 0, . . . , 3, e mη ≤

√ 2 mπ,

con m la massa dei quark (supposta uguale). Ma anche questo non accade, infatti vale √2 mπ ¿ mη. Questa situazione `e nota come problema U(1).

In un primo tempo si pens`o che il mesone η potesse essere il bosone di Goldstone, ma la sua massa eccessiva non era ammissibile. Il motivo `e che, essendo la simmetria U(1) rotta dallo stesso termine di massa che rompe quella SU (2) ⊗ SU(2), dovremmo avere per il quarto bosone di Goldstone circa la stessa massa dei pioni.

Il fatto che la (1.22) presenti l’anomalia triangolare di Adler-Bell-Jackiw, dovuta alla presenza di termini aggiuntivi richiesti dalla sua rinormaliz-zazione, fa s`ı che nel limite di N quark a massa nulla, si abbia

∂µ_j5 µ = 2Ng2 64π2 ² µνρσ_Ga µν(x) Gaρσ(x) . (1.23) La quantit`a Q(x) = Ng 2 64π2 ² µνρσ_tr³_G µν(x) Gρσ(x) ´ ,

in cui la traccia `e calcolata sugli indici di colore, `e definita densit`a di carica topologica e il suo integrale

Q = Z

`e la carica topologica.

La (1.23) mostra che la corrente non `e conservata. Tuttavia `e possibile scrivere il secondo membro della (1.23) come la divergenza di una corrente gauge variante formata da Aµ e Gµν per ottenere cos`ı la corrente

J5 µ = jµ5 − 2NKµ, dove Kµ= g2 16π2 ² µαβγ_Aa α ³ ∂βAaγ− 1 3g f abc_Ab βAcγ ´ , (1.25) per cui vale

Q = ∂µKµ. (1.26)

La corrente J5

µ`e conservata ma non `e gauge invariante. Per funzioni di Green

contenenti J5

µ e campi di quark si possono ottenere le identit`a di Ward chirali

U(1) nella forma usuale, che portano a concludere che o le funzioni di Green associate a soli campi fermionici sono invarianti sotto U(1) o che si hanno poli associati ai bosoni di Goldstone nelle funzioni di Green associate a J5

µ e

a stringhe di campi fermionici [1] p. 309.

Vedremo che, grazie alla presenza degli istantoni e al fatto che la corrente (1.25) non `e gauge invariante, il problema del bosone di Goldstone mancante verr`a risolto.

1.4

Istantoni

Qualsiasi modello di vuoto in QCD dovrebbe almeno spiegare il meccanismo del confinamento e della rottura della simmetria chirale. Alla base dei molti modelli proposti per comprendere lo stato di vuoto della QCD vi `e l’idea che il vuoto `e dominato da campi di gauge classici (come ad esempio, il “campo costante”, oppure regioni di campi costanti connesse fra loro, come nello “Spaghetti vacuum”, introdotto dal Kopenhagen group). Tutti questi

tentativi si sono rivelati infruttuosi, essendo i campi costanti instabili se si applica la teoria perturbativa.

Gli istantoni sono soluzioni classiche delle equazioni euclidee del moto. Esse sono caratterizzate da una carica topologica e corrispondono a “tunnel-ings event” fra stati classici degeneri di vuoto nello spazio di Minkowski.

Nel limite semiclassico l’integrale (1.10) `e dominato dalle soluzioni staziona-rie dell’azione S definita in (1.9). Iniziamo la loro ricerca non considerando la parte fermionica dell’azione e poniamo A4 = 0 (gauge temporale).

Passando da una formulazione lagrangiana ad una hamiltoniana otte-niamo H = 1 2g2 Z d3_{x (E}2 i + Bi2) , dove Ei = ∂4Ai, Bi = 1 2²ijkGjk. (1.27) Si vede che le soluzioni in cui Aµ `e nullo minimizzano la (1.27).

Esiste tuttavia la possibilit`a di operare sulle nostre soluzioni una trasfor-mazione di gauge indipendente dal tempo che quindi conservi il vincolo A4 = 0. Otteniamo cos`ı le soluzioni di pura gauge

Aµ = i Ω(¯x) ∂µΩ+(¯x) , (1.28)

dove Ω `e definito in (1.2).

Una caratteristica fondamentale di queste soluzioni `e che possono essere suddivise in classi di omotopia. Due funzioni appartengono alla stessa classe di omotopia se possono essere deformate con continuit`a una nell’altra. I campi Aµ in (1.28) sono mappature dallo spazio S3 nello spazio SU(N) . Invece di considerare SU(N) come spazio di arrivo, analizziamo il caso pi`u semplice delle funzioni S3 → SU(2) (in realt`a stiamo studiando S3 → S3 in quanto SU(2) `e topologicamente equivalente a S3).

Mappature del tipo            Ω0_{(x) = 1,} Ω1_{(x) =} x4 _√+ i ¯x ¯σ x2 , Ων_{(x) = [Ω}1_(x)]ν_{, per ν > 1.}

sono dette standard. Vale la propriet`a che ogni mappatura da S3 a S3 `e omotopica ad una standard.

Allo scopo di svincolarci da una dimensione particolare del gruppo SU(N), si introduce il “prodotto di Cartan” definito da

(Ta, Tb) = tr (TaTb) = δab. (1.29) Definiamo il numero n (winding number)

n = 1 48 π2 Z dθ1dθ2dθ3²ijk(Ω ∂iΩ−1, Ω ∂jΩ−1Ω ∂kΩ−1). (1.30) risulta che - n `e un invariante omotopico,

- per Ω posto uguale ad una mappatura standard si ha n = ν.

Perci`o le mappature standard individuano delle classi di omotopia a ciascuna delle quali si pu`o associare ν come winding number.

Richiamando la (1.25), si pu`o verificare che Z

d4_{x (G}

µν, ¯Gµν) = 32 π2ν , dove G¯µν =

1

2²µνλσGλσ. (1.31) Torniamo adesso al caso generale SU (2) → SU(N), per il quale possiamo fare uso di un teorema dovuto a Raoul-Bott: per un qualsiasi gruppo di Lie semplice G, ogni mappatura continua S3 → G pu`o essere deformata con continuit`a in una mappatura di un sottogruppo SU(2) di G. Quindi, con

una appropriata definizione dei prodotti di Cartan interni, possiamo usare la stessa definizione di winding number ricavata per SU(2) anche nel caso SU (N).

Abbiamo cos`ı visto che:

- i campi di pura gauge sono stati che minimizzano l’azione con win-ding number univocamente associato e calcolabile mediante le (1.30) e (1.31),

- se usiamo Ω(x) come trasformazione di gauge sul campo nullo, otteniamo lo stato di vuoto | Ω > con winding number nΩ.

Per semplicit`a torniamo a usare il gruppo SU(2). Sapendo che tr

Z

d4x (Gµν ± ¯Gµν)2 ≥ 0 ,

dalla (1.31) segue che ¯ ¯ ¯ tr Z d4x GµνGµν ¯ ¯ ¯ ≥ ¯ ¯ ¯ tr Z d4x (GµνG¯µν) ¯ ¯ ¯ = 32 π2n. Quindi l’azione euclidea soddisfa

S(A) ≥ 8π2n g2 .

L’uguaglianza fra i due membri si ha quando Gµν = ± ¯Gµν, ossia quando il

campo `e selfduale (col segno positivo) e anti-selfduale (col segno negativo). In questo caso l’azione `e minimizzata e grazie all’identit`a di Bianchi si ha che le equazioni del moto DµGµν = 0 sono soddisfatte.

Usando la corrente Kµdefinita in (1.25), per un campo selfduale si mostra

che n = Z d3_{x K} 4(¯x, t = +∞) − Z d3_{x K} 4(¯x, t = −∞) (1.32) ∝ nΩ(t = +∞) − nΩ(t = −∞) .

Quindi a causa della (1.26) per tale campo la soluzione associata connette stati di vuoto con differente carica topologica.

Cerchiamo allora soluzioni di pura gauge che rispettino la condizione di (anti)selfdualit`a. Sappiamo che

lim x→∞ g τa 2 A a µ = i Ω ∂µ Ω+, con Ω = i τ+ µxµ √ x2 , τ ± µ = (¯τ , ∓ i).

Mediante i simboli di ’t Hooft (ved. appendice A) il comportamento asin-totico di Aa

µ pu`o essere scritto

lim x→∞ A a µ → 2 g ηaµν xν x2 .

Se cerchiamo una soluzione a simmetria sferica possiamo ipotizzare per Aa µ(x)

una forma di questo tipo Aa_µ(x) = 2 gηaµν xν x2 f (x 2_{) , con lim} x2_→∞ f (x 2_{) = 1, lim} x2_→0 f (x 2_{) = cost x}2_. Otteniamo allora Ga µνGaµν = − 4 g n ηaµν f (1 − f ) x2 + xµηaνγxγ − xνηaµγxγ x4 [f (1 − f ) − x 2_f0_]o ¯ Ga µν = − 4 g n ηaµνf0 − xµηaνγxγ − xνηaµγxγ x4 [f (1 − f ) − x 2_f0_]o_. (1.33) Le formule usate per derivare le (1.33) si trovano in appendice A.

La condizione di selfdualit`a Ga µν = ¯Gaµν impone che f (1 − f ) − x2f0 = 0 , da cui deriviamo f (x2_{) =} x2 x2 _{+ ρ}2,

in cui ρ `e un parametro arbitrario. L’invarianza sotto traslazione fa s`ı che la soluzione con centro in un punto arbitrario x0 si possa ottenere sostituendo

(¯x − ¯x0) a ¯x nel modo seguente Aa µ = 2 g ηaµν (x − x0)ν (x − x0)2 + ρ2 , (1.34) a cui `e associato Ga µν = − 4 g ηaµν ρ2 [(x − x0)2 _{+ ρ}2_]2 .

Operando una trasformazione di gauge (detta singolare) con una U(x) tale che per x → ∞ valga

U(x) = Ω(x),

otteniamo una soluzione che presenta una singolarit`a in x0 (necessaria al fine di connettere stati di vuoto con cariche topologiche differenti) della forma

¯ Aa_µ = 2 g η¯aµν (x − x0)νρ2 (x − x0)2[(x − x0)2 + ρ2] , (1.35) con ¯ Ga µν = − 8 g h(x − x0)µ(x − x0)ν (x − x0)2 − 1 4δµν i ¯ ηaµν ρ2 [(x − x0)2 + ρ2]2 − (µ ↔ ν),

dove ¯ηaµν `e un simbolo di ’t Hooft (ved. appendice A). La (1.35) viene

definita istantone con centro nel punto x0 e larghezza ρ. Si definisce anche l’anti-istantone come il trasformato sotto parit`a dell’istantone [1] p. 318.

Abbiamo dunque trovato alcune soluzioni della teoria di campo classica (DµGµν = 0), che connettono stati di vuoto con differenti winding number.

Le soluzioni appena individuate possiedono un certo numero di gradi di libert`a, associati alla simmetria dell’azione, detti variabili collettive. Deter-mineremo queste variabili, che risultano importanti per il calcolo dei valori di aspettazione degli osservabili.

Vediamo subito che, grazie al gi`a citato teorema di Raoul Bott, possi-amo cominciare la nostra ricerca dal caso semplice di SU(2), in quanto un

istantone `e una funzione S3 → SU (N) omotopica ad una S3 → SU (2) . Quindi, una volta studiato il caso SU(2), baster`a capire quante e quali siano le variabili libere introdotte dai generatori che vengono “aggiunti” passando al caso SU(N).

1.4.1

Caso SU (2)

1. Le soluzioni (1.34) dipendono dal parametro arbitrario ρ.

2. Come abbiamo gi`a detto, se Aa

µ(x) `e soluzione, anche Aaµ(x − x0) lo `e.

Quindi abbiamo, oltre a ρ , altri quattro parametri liberi.

3. Operando un cambiamento di gauge globale, otteniamo nuovamente una soluzione istantonica Aµ→ U AµU+.

4. Si dimostra che le rotazioni di x non generano nuove soluzioni. Questo perch´e le rotazioni quadrimensionali possono sempre essere annullate dalle rotazioni nel gruppo del colore.

Dimostriamo quest’ultimo punto. Sotto trasformazioni di gauge, si ha Aµ(x) → Ω(x) ˆAµ(x) Ω+(x) − i/g(∂µΩ(x) ) Ω+(x).

Se operiamo sui campi Aµ e Ω la seguente trasformazione globale

Ω(x) → Ω(x) U₁+, Aˆµ(x) → U1+, con U+

1 indipendente da x, abbiamo che Aµ(x) resta invariato. Un’altra

trasformazione che lascia invariata la teoria `e

Ω(x) → U2Ω(x) , Aˆµ(x) → ˆAµ(x) ,

Quindi sotto U1 ∈ SU(2) abbiamo che Ω(x) trasforma come la rappre-sentazione (1/2) e ˆAµ(x) come la (1). Invece sotto U2 ∈ SU (2) abbiamo che

Ω(x) ∈ (1/2) e ˆAµ ∈ (0). Il gruppo delle rotazioni nello spazio Euclideo

4-dimensionale `e SU (2)NSU(2). Risulta cos`ı che, scelti 6 parametri per la trasformazione in SU (2)NSU(2) dello spazio Euclideo, possiamo deter-minare altri 6 parametri nel gruppo U1NU2 (SU(2)NSU(2)) per fare in modo che ix√µτ µ

x2 rimanga invariato. Dato che quest’ultima `e la base di partenza per formare le soluzioni istantoniche, vediamo che le rotazioni in R4 <sub>non aggiungono nuove variabili collettive a quelle derivanti dal gruppo di</sub> colore. Risulta cos`ı dimostrato il punto 4.

Quindi, condiderando che U1non fornisce nuove soluzioni, i gradi di liber-t`a effettivi sono quelli associati a U2. Poich´e U2 ∈ SU (2), avremo 3 gradi di libert`a.

1.4.2

Caso SU (N )

Andiamo poi a considerare il caso SU(N). Le 5 variabili collettive dovute all’invarianza di scala e all’invarianza sotto traslazioni non subiscono cambia-menti. Consideriamo la rappresentazione matriciale dei generatori di SU(N), che pu`o essere cos`ı scomposta a blocchi

2 N − 2 z}|{ z }| {         A C C B         o          2 N − 2

cam-po istantonico, siano raggruppati nella zona A. `E chiaro che gli unici gene-ratori del gruppo con la possibilit`a di ruotare quelli del sottogruppo SU(2) sono invece raggruppati in C.

Quindi alle 3 rotazioni di SU(2) dobbiamo sommare altre 4(N − 2) ro-tazioni unitarie. Il numero totale di modi zero nel caso SU(N) `e allora (N2<sub>− 1) − (N − 2)</sub>2 <sub>+ 5 = 4N, dove (N</sub>2<sub>− 1) `e il numero di generatori di</sub> SU (N) e (N − 2)2 _{`e il numero di generatori che commutano con quelli che} hanno elementi diversi da 0 solamente in A.

1.5

Modi zero fermionici

In presenza di fermioni leggeri gli istantoni sono associati ai modi zero fermio-nici. I modi zero fermionici sono essenziali nella comprensione dell’anomalia assiale ma anche nella rottura spontanea della simmetria chirale. Infatti quando gli istantoni interagiscono attraverso scambio di fermioni i modi zero possono divenire delocalizzati formando cos`ı un condensato di quark.

Una schematizzazione della dinamica dei quark nel vuoto vede gli istan-toni agire come una barriera di potenziale in cui i fermioni possono formare stati legati (modi zeri). Se gli istantoni formassero una rete abbastanza fitta, i quark leggeri potrebbero spostarsi per lunghi tratti utilizzando gli istantoni come tramite. Vediamo quindi che gli istantoni possono fornire una com-prensione qualitativa di molti aspetti del livello fondamentale della QCD e delle sue eccitazioni.

Definiamo prima gli stati | n > che sono quelli associati alla configu-razione Aa

µ di pura gauge con winding number n. Uno stato | n > si pu`o

ot-tenere dal campo Aa

µ = 0 operando una trasformazione di gauge indipendente

Si osserva che, essendo gli stati | n > connessi fra di loro dagli istantoni, lo stato fondamentale in QCD non potr`a che essere una sovrapposizione di | n >. Se infatti consideriamo gli istantoni abbastanza diluiti, possiamo scrivere l’ampiezza di transizione da | n > a | m > in questo modo

< n | e(−Hτ )_{| m > =} X N+ X N− δN+−N−−n+m N+! N−! (Kτ e−S₎N+−N−_,

dove K `e il fattore pre-esponeziale dell’integrale di Gauss derivante dal formalismo di path-integral e N± `e il numero di istantoni e anti-istantoni.

Usando l’identit`a δ(N+−N−) (−n+m) = 1 2π Z _2π 0 dθ ei θ ((N+−N−)−(−n+m))_, otteniamo < n | e−Hτ_{| m > =} 1 2π Z _2π 0 dθ ei θ (n−m)_e2Kτ cos(θ) exp (−S)_{. (1.36)} Se adesso consideriamo il nuovo insieme di stati

| θ > ≡ X

n

einθ_{| n > ,}

e inseriamo la sua relazione di completezza nel primo membro di (1.36) vediamo che gli stati | θ > sono autofunzioni dell’energia con autovalori

E(θ) = −2 K cos(θ) exp (−S) . (1.37) Tornando all’introduzione dei campi fermionici, mettiamoci in una ver-sione semplificata della (1.1), in cui il gruppo di colore sia SU (2) e si abbia un unico isodoppietto di quark a massa nulla. L’azione in questo caso diviene

S = Z

d4_xh 1

4g2 (G, G) − i ¯ψ (∂µD

µ_{) ψ}i_,

dove il prodotto di Cartan `e definito in (3.2). Gli istantoni sono ancora soluzioni delle equazioni euclidee del moto (con i campi ψ posti uguali a zero). Abbiamo quindi che gli stati | θ > sono ben definiti e la formula (1.37) continua a valere.

Si vede che nelle funzioni di correlazione compare un fattore (1.11) pro-porzionale a det hi γνDν i γν∂ν i = det hi γν(Aν + ∂ν) i γν∂ν i ,

dove Aν _{`e il campo di un istantone. Dimostreremo adesso che questo fattore}

`e zero a causa della presenza di autofunzioni con autovalore nullo di γνDν.

Possiamo assumere 1_{, che gli autovalori λ}

r in i γνDνψr = λrψr siano

discreti. Poich´e i γνDν `e hermitiano, λr `e reale.

Visto che γν anticommuta con γ5, si ha che i γνDνγ5ψr = −λrγ5ψr.

Quindi autovalori non nulli si presentano sempre in coppie di segno opposto. D’altra parte autofunzioni associate ad autovalori nulli possono sempre essere scelte in maniera tale da essere autofunzioni di γ5

γ5ψr = ζrψr, (λr = 0) .

Essendo γ2

5 = 1, si ha ζr = ± 1. Denoteremo il numero di autofunzioni di

questi due tipi con n±.

Il prossimo obiettivo `e dimostrare che se ν `e il winding number del campo istantonico, allora

n− − n+ = ν, (1.38)

che equivale a provare l’esistenza di autovalori nulli di γνDν.

Ricaviamo dunque la (1.38). Cominciamo scrivendo le identit`a di Ward chirali nel caso di un campo di quark massivo interagente con un campo di gauge esterno. Consideriamo la trasformazione

δψ = −iγ5ψ δα, δ ¯ψ = −i γ5ψ δα ,¯ (1.39) con δα una funzione infinitesimale nello spazio euclideo. La corrente ad essa associata `e

1_{Questa ipotesi non `e propriamente esatta, ma si pu`o dimostrare, con un procedimento}

j_µ5 = ¯ψ γµγ5ψ. (1.40)

La (1.39) nel caso di massa m non nulla non `e un’invarianza del sistema. Si ha quindi che la (1.40) non `e conservata

∂µjµ5 = ¯ψ mγ5ψ . `

E possibile (ved. [1], cap. 5.3), studiando la divergenza di D

j_µ5(y)ψ(1)(x1) . . . ψ(n)(xn)

E , in cui i campi ψ(1)_(x

1), . . . , ψ(n)(xn) sono funzioni multilineari locali dei

campi ψ(y), ottenere le identit`a di Ward ∂µ D j5 µ(y)ψ(1)(x1) . . . ψ(n)(xn) E_A + D ¯ ψ m γ5ψ(y) ψ(1)(x1) . . . ψ(n)(xn) E_A + δ(4)_{(y − x} 1) D ∂ ψ(1)_(x 1) ∂ α . . . ψ (n)_(x n) E_A + . . . + δ(4)_{(y − x} n) D ψ(1)_(x 1) . . . ∂ ψ(n)_(x n) ∂ α A = i C 8π2 (G(y) , ¯G(y)) D ψ(1)(x1) . . . ψ(n)(xn) E_A , (1.41)

dove l’indice A sta ad indicare che stiamo lavorando in un campo di gauge esterno. La costante C `e definita in maniera tale che tr λa_λb _{= −Cδ}ab_{. Nel}

caso di N campi `e C = N/2. Nel nostro caso C = 1/2.

Se adesso integriamo rispetto a y l’equazione (1.41), ricordando che Z d4_{y (G, ¯G) = 32 π}2_ν, otteniamo 2D R d4_{y ¯ψ(y) m γ} 5ψ(y) ψ(1)(x1) . . . ψ(n)(xn) E_A + ∂ ∂ α < ψ (1)_(x 1) . . . ψ(n)(xn) >A = −4 i C ν < ψ(1)_(x 1) . . . ψ(n)(xn) >A. (1.42)

A questo punto, se consideriamo il caso in cui gli ψ(r) _{sono assenti, la (1.42)} diviene −2iν = 2 D Z d4_{y ¯ψmγ} 5ψ E_A = 2 R [dψ] [d ¯ψ] e−S R _d4_{y ¯ψ m γ5ψ} R [dψ] [d ¯ψ] e−S .

Se espandiamo dψ e d ¯ψ in termini delle autofunzioni di i(γµDµ− m)ψr = (λr− im)ψr, otteniamo −2 i ν = 2 m P_r Z d4_{y ψ}+ r γ5ψr Y s6= r (λs − im) Q r(λr − i m) (1.43) = 2 mX Z d4_{y ψ}+ r γ5ψr(λr − i m)−1. (1.44)

Nel caso λr 6= 0 otteniamo

Z

d4y ψ+_r γ5ψr = 0.

Nel caso λr = 0 otteniamo

Z

d4_{y ψ}+

r γ5ψr = ζr.

Quindi −2iν = 2i(n+− n−). Abbiamo cos`ı ricavato la (1.38).

Utilizzando la (1.24), si ottiene la seguente relazione

Q = n− − n+ ≡ index(D), (1.45) nota come teorema dell’indice di Atiyah-Singer.

Vediamo dunque, che in presenza di un qualsiasi campo di gauge esterno con winding number diverso da zero si deve necessariamente avere un auto-valore nullo. Nel caso particolare di un campo di gauge esterno istantonico si ha n− = 1 e n+ = 0. Il fatto che E(θ) = 0 per ogni θ `e associato al fatto che vale _· ∂ ∂x + 2 ∂ ∂y ¸_­ θ | ψ(1)_(x 1) . . . ψ(n)(xn) | θ ® = 0.

Quindi U(1) `e rotta spontaneamente e gli stati θ sono gli stati di vuoto degeneri.

Un metodo alternativo pi`u diretto per verificare l’esistenza di autovalori zero (o modi zero) `e quello di risolvere l’equazione i γµDµu0 = 0. Seguendo

questa strada si ottiene per un istantone con centro in x0 e larghezza ρ ψ0(x − x0, ρ) = ρ

£

ρ2 + (x − x0)2 ¤_−2/3

u , dove u `e uno spinore costante.

1.6

Dipolo di Goldstone

Consideriamo

< θ | σ+(x) σ−(0) | θ > , dove σ±(x) =

1

2ψ (1 ± γ5) ψ.¯

Abbiamo solo due configurazioni istantoniche che danno risultato diverso da zero: Aµ_{= 0 e quella costituita da un istantone pi`u un anti-istantone. Si pu`o}

verificare [1] p. 322, che in entrambi i casi non sono presenti poli associati a bosoni di Goldstone e che inoltre lo stesso avviene in qualsiasi funzione di Green invariante di gauge. Se invece consideriamo la funzione di Green

< θ | J5

µσ−(0) | θ > = < θ | jµ5σ−(0) | θ > +

i

16π2 < θ | Kµ(x) σ−(0) | θ > , con J5

µ, jµ5 riferite alla (1.25), otteniamo al secondo termine del secondo

membro un polo di Goldstone.

Condizione necessaria e sufficiente per avere questo in una gauge

cova-riante `e _Z

d4x ∂µ< θ | Kµ(x) σ−(0) | θ > 6= 0 . (1.46)

Questo si pu`o dimostrare usando Z

d4_{x ∂}

e il fatto che l’unica configurazione che contribuisce alla (1.46) `e quella con ν = 1. Abbiamo cos`ı

Z

d4_{x ∂}

µ < θ | Kµ(x) σ−(0) | θ > = 32π2 < θ | σ−| θ > 6= 0 .

Quindi, nel limite di massa nulla e utilizzando l’approssimazione di gas diluito [1] p. 320, otteniamo che le funzioni di Green associate a quantit`a fisiche osservabili (invarianti di gauge) non presentano bosoni di Goldstone mentre quelle non invarianti di gauge s`ı. In questo caso si dice che `e presente un dipolo di Goldstone. La simmetria U(1) chirale `e rotta spontaneamente in modo anomalo.

Abbiamo ottenuto questo risultato per SU (2). Passare al gruppo SU(3) non `e difficile. L’unica cosa che dobbiamo cambiare `e il termine g−8_{, che}

diviene g−12_{. Invece il fatto che i quark leggeri siano due comporta maggiori}

modifiche. I campi fermionici indipendenti sono due, quindi ad ogni istantone sono associati due modi zero fermionici. Questo fa s`ı che i valori di aspet-tazione che prima erano diversi da zero come < θ | σ±(x) | θ > ora siano uguali

a zero. Il problema comunque `e solamente tecnico, baster`a infatti considerare le funzioni di Green di elementi del tipo ¯ψ1(1 − γ5) ψ1ψ¯2(1 − γ5) ψ2 per verificare che U(1) `e rotta spontaneamente. Inoltre, come nel caso precedente U(1) `e rotta in maniera anomala.

Quanto visto rappresenta una soluzione del problema U(1), che per`o `e di difficile verificabilit`a a causa del fatto che la QCD non ha soluzione esatta analitica.

Fermioni di Ginsparg-Wilson

Scopo di questo capitolo `e derivare la formula di Witten-Veneziano (WV). La validit`a della formula `e un test cruciale per la QCD, visto che mette in relazione il fatto che la massa di η0 _{non si annulli nel limite chirale con la}

rottura esplicita della simmetria U(1) assiale che, come abbiamo visto nel capitolo 1, `e indotta a livello quantistico dall’anomalia gluonica. Dopo aver presentato la formula di WV (paragrafo 1), si introduce la QCD su reticolo (paragrafo 2) e le relazioni di Ginsparg-Wilson (paragrafo 3), fondamentali per preservare le simmetrie chirali su reticolo. Nel paragrafo 4 si riscrive la formula di WV nel contesto del reticolo. Nell’ultimo paragrafo si discute del problema U(1) su reticolo.

2.1

Formula di Witten-Veneziano sul continuo

La formula di WV [34], [35] lega la massa di η0 _{alla carica topologica.}

Ripren-diamo quindi le definizioni date nel capitolo 1 di densit`a di carica topologica Q(x) = Ng 2 32π2 ² µνρσ_tr³_G µν(x) Gρσ(x) ´ , (2.1) 33

in cui la traccia `e calcolata sugli indici di colore, e di carica topologica Q =

Z

d4_{x Q(x). (2.2)}

A partire da Q(x) si definisce la suscettivit`a topologica χ =

Z

d4_x ­_{0 | T (Q(x)Q(0) | 0}®_{. (2.3)} La sua trasformata di Fourier

χ(p) = Z

d4x eixp­0 | T (Q(x)Q(0) | 0® (2.4) `e detta suscettivit`a topologica a impulso p.

Per derivare la formula di WV sul continuo, si parte dalla regola di singo-letto di sapore WTI, in cui compare l’autocorrelazione topologica­Q(x)Q(0)®

∂µ ­ A0 µ(x)Q(0) ® = 2mq ­ P0_(x)Q(0)® _{+ 2N} f ­ Q(x)Q(0)®, (2.5) dove A0 µ = Nf X r=1 ¯ ψr_γ µγ5ψr `e la corrente assiale, P0 = Nf X r=1 ¯ ψrγ5ψr

`e la densit`a di singoletto di quark pseudo-scalare e mq `e la massa di quark.

`

E sottinteso che tutti gli operatori nella (2.5) sono finiti per x 6= 0. La trasformata di Fourier della (2.5) nel limite chirale `e

ipµ Z d4x e−ipx­A0_µ(x)Q(0)® + CT (p) = 2Nf R d4_{x e}−ipx­_Q(x)Q(0)® _{+ CT (p) ≡ 2N} fχ(p). (2.6)

Il termine CT (p), che `e stato aggiunto ad entrambi i membri per renderli separatamente finiti, `e un polinomio di grado 4 in p che si annulla per p = 0,

visto che la trasformata di Fourier del primo membro della (2.5) `e, secondo la teoria, finita (in realt`a zero) per p = 0. Vedremo in seguito che CT (p) non gioca alcun ruolo, a causa del fatto che ci`o che ci interessa `e il valore di χ(p) per p = 0.

L’assenza di particelle a massa nulla nel canale di singoletto pseudo-scalare implica che

χ(0) = 0. (2.7)

Questa importante relazione mostra che la suscettivit`a topologica in QCD si annulla nel limite chirale.

Da questa relazione si pu`o derivare una formula per la massa di η0 _quando

la suscettivit`a topologica in assenza di quark `e diversa da zero. In questa situazione, infatti, posto µ = Nf/Nc l’azzeramento di χ(p) per p = 0 nella

QCD ad ogni ordine in µ pu`o verificarsi solo se esiste un contributo mesonico a χ(p) la cui massa va a zero linearmente per µ → 0. Perci`o il limite per p → 0 e l’espansione di χ(p) intorno a µ = 0 non commutano.

Si pu`o dimostrare [9] che χ(p) pu`o essere scritta nella forma χ(p) = χ(0) + χ0_(0)p2 ₊1

2χ

00_(0)(p2₎2_{+ (p}2₎3_{I, (2.8)}

dove I `e l’integrale di dispersione che coivolge la parte immaginaria di χ(p). Separando il contributo di η0 _{dal resto, scriviamo I nella forma}

I ≡ R 2 η0 (m2 η0)3(p2+ m2_η0) + ˜I, dove −R2

η0 `e il residuo del polo η0 che `e definito negativo nella metrica

euclidea.

Si `e gi`a osservato che i limiti per p → 0 e per µ → 0 non commutano. Faremo allora prima il limite della (2.8) per µ → 0 e poi per p → 0. Poich´e p 6= 0, prendere il limite del primo membro della (2.8) per µ → 0 `e equivalente

ad eliminare i contributi del determinante fermionico. Abbiamo quindi che χ(p)|quenched= lim

u→0χ(p).

Al secondo membro della (2.8) espandiamo, tenendo fisso p2_{, il contributo di} η0 _{in potenze di m}2

η0/p2 = O(u/p2) e uguagliamo i termini nelle potenze di p2

con i corrispondenti termini dell’espansione di Taylor di χ(p)|quenched attorno a p2 _{= 0. Si ottiene} χ(0)|quenched= lim u→0 h χ(0) + R 2 η0 m2 η0 i .

Il termine ˜I non contribuisce in quanto `e una funzione che si annulla per p → 0 con le sue prime due derivate. Supponendo che le quantit`a che compaiono al secondo membro abbiano limite finito per µ → 0, si ha

R2

η0

m2

η0

= χ(0)|quenched − χ(0) + O(u). (2.9) Come vediamo qui di seguito, le due relazioni (2.7) e (2.9) costituiscono la base per ottenere la formula WV. Ricordiamo che vale la formula

R2

η0 =

¯ ¯

¯­0| ˆQ|η0®¯¯_¯2_.

Si scrivono gli elementi della matrice ˆQ in termini dei corrispondenti elementi della matrice della divergenza della corrente assiale di singoletto di sapore, e si usano le relazioni PCAC [5] p. 274. Nel limite chirale si ottiene

2Nf ­ 0| ˆQ|η0®₌­_0|∇µ_Aˆ0 µ|η0 ® . (2.10)

Il secondo membro pu`o essere espresso in termini della costante di decadi-mento per il mesone pseudo-scalare Fπ.

D’altra parte, per derivare la formula di WV, ci interessa solo calcolare R2

η0 nel limite µ → 0, in cui F_π coincide con F_η0. Combinando l’equazione

­

0|∇µ_Aˆ0

µ|η0

®

che `e la definizione di Fη0, con la (2.10) si ottiene R2 η0 m2 η0 ¯ ¯ ¯ u=0= F2 η0m2_η0 2Nf ¯ ¯ ¯ u=0 = F2 πm2η0 2Nf ¯ ¯ ¯ u=0. (2.11) Ricordando che Fπ = O( √

2Nc) a meno di termini di ordine superiore in u,

si ha che R2

η0/m2_η0

¯ ¯

u=0= O(1). Dalle (2.9) e (2.11) si ottiene

m2_η0 = 2Nf F2 π χ(0) ¯ ¯ ¯ quenched+ O(u 2_{). (2.12)}

La (2.12) costituisce la formula di WV. Questa formula non pu`o essere uti-lizzata su reticolo a causa del fatto che il secondo membro `e zero su volumi finiti, visto che su volumi finiti non ci sono particelle a massa nulla, ma pu`o essere messa in una forma adatta ad essere utilizzata su reticolo. Infatti, nell’approssimazione quenched l’integrale al secondo membro della (2.12) `e dato nel limite chirale dal contributo del polo della particella di singoletto pseudo-scalare, in quanto la massa di questa particella si annulla in questo limite. Ne segue che la (2.12) pu`o essere scritta nella forma

m2 η0 = p 2Nf Fπ ­ 0|Q|η0®¯¯_¯ quenched. (2.13)

In questa formula `e scomparso ogni riferimento al volume in cui il sistema `e racchiuso, pertanto la (2.13) pu`o essere utilizzata su reticolo, ridefinen-do opportunamente la carica e la suscettivit`a topologica, come vedremo nei prossimi paragrafi.

2.2

Formulazione di QCD su reticolo

2.2.1

Rinormalizzazione su reticolo

Come accennato nel primo capitolo, utilizzare il reticolo significa discretizzare tutte le 4 dimensioni dello spazio-tempo, ottenendo cos`ı un reticolo di N4 _siti

a distanza reticolare a. Le coordinate dei siti sono xµ= nµa, − N 2 < nµ≤ N 2 , in cui nµ ha le 4 componenti intere.

La trasformata di Fourier di una funzione f (n) definita sul reticolo `e ˆ f (k) =X n f (n)eikn_{, k} µ = 2π N qµ, − N 2 < qµ≤ N 2 . Quindi f (n) = 1 N4 X k ˆ f (k)e−ikn.

Il reticolo agisce come regolarizzatore della teoria. In particolare il parametro a ha il ruolo di costante di regolarizzazione, come lo aveva l’² introdotto nel paragrafo 1.2.

Sappiamo quindi che dovremo mandare a zero a e usare un metodo di rinormalizzazione. Sul reticolo questo procedimento presenta delle partico-larit`a che ora discuteremo.

Supponiamo di voler calcolare il valore di un osservabile O di dimensione dO in unit`a del passo reticolare a su reticolo. Calcolando il suo valore < O >

si ottiene un risultato della forma

< O >= adOf O(g),

dove fO(g) `e una funzione adimensionale della costante di accoppiamento

della teoria (che pu`o essere anche pi`u di una). Se ad esempio O fosse una lunghezza di correlazione del modello avremmo dO = 1 e fO(g) misurerebbe

la lunghezza di correlazione in unit`a del passo reticolare per un dato g. Se per ottenere il limite continuo si mandasse semplicemente a zero a, si otterrebbe < O >= 0. Quindi g deve essere, a sua volta, funzione di a e per a → 0 la costante di accoppiamento g deve tendere a un valore critico gc su cui

la lunghezza di correlazione misurata in unit`a del passo reticolare tende a infinito.

`

E chiaro che la dipendenza di g da a deve essere tale da rendere finito qualsiasi operatore Oi misurato in unit`a di passo reticolare, quando si prenda

il limite al continuo. Questa richiesta fissa in maniera precisa la dipendenza funzionale fra a e g che, come `e stato detto, `e la stessa a prescindere dall’ope-ratore che viene misurato. Proprio questo fatto permetterebbe in principio di poter non conoscere g(a). Infatti basta utilizzare un osservabile il cui valore fisico `e ben noto, ad esempio una massa me, per fissare la scala della teoria

utilizzando

me =

1 a(g)λe(g)

,

dove λe(g) `e la lunghezza di correlazione associata alla me. Quindi il limite

continuo di un osservabile dimensionale, come ad esempio la massa mi di

un’altra particella, pu`o essere ottenuto nel seguente modo mi = lim a→0 1 a(g)λi(g) = lim g→gc λe(g) λi(g) me.

Tuttavia nel caso delle teorie di gauge non abeliane, per cui il fenomeno della libert`a asintotica ci dice che gc= 0, `e possibile utilizzare metodi perturbativi

per ricavare esplicitamente g(a). Per una teoria di pura gauge SU(N) in quattro dimensioni si ha ad esempio

a = 1 Λf (g), (2.14) in cui f (g) =¡β0g2 ¢_−β1/(2β2 0)_e−1/(2β0g2)¡_{1 + O(g}2₎¢_{, (2.15)} dove β0 = 11Nc 48π2, β1 = 34 3 h Nc 16π2 i₂ ,

sono i primi due coefficienti della funzione di Callan-Symanzik β(g) e Λ `e un parametro di scala che dipende dallo schema di rinormalizzazione scelto. Questo permette di usare solo il parametro adimensionale

β = 2Nc g2 ,

mediante il quale si pu`o variare a (“trasmutazione dimensionale”). La re-lazione fra β e a risulta quindi del tipo Λa = f (β). Ne segue che misurando una quantit`a O di dimensione non nulle in massa d a diversi valori di β, si `e in un intorno di gc se O segue una legge proporzionale a f (β)−d .

Ovviamente il limite continuo di O si ottiene per β = ∞. A β grandi, per`o, si ha per (2.14) e (2.15) che un fermi diventa molto grande rispetto ad a e quindi `e necessario utilizzare reticoli le cui dimensioni crescono esponen-zialmente con β. Inoltre sempre per β grandi, le quantit`a fisiche hanno l’an-damento f (β)−d <sub>e quindi divengono molto piccole, richiedendo cos`ı l’impiego</sub>

statistiche esponenzialemente grandi per minimizzare gli errori.

Per ottenere delle misure bisogna quindi utilizzare valori di β per cui un fermi sia abbastanza grande rispetto al passo reticolare ma allo stesso tempo contenuto nel reticolo (che non deve essere troppo grande). Un tale insieme di β, se esiste, si chiama finestra di scaling e i valori di O calcolati in essa possono essere legati a quelli associati a β = ∞ tramite coefficienti di rinormalizzazione.

In conclusione, per estrarre valori fisici dal reticolo bisogna fare due passi. - Nel primo bisogna definire su reticolo le quantit`a a cui siamo interessati. Questo pu`o essere fatto in vari modi (noi affronteremo il caso della carica e della suscettivit`a topologica).

- Nel secondo le misure fatte sulle quantit`a scelte devono essere messe in relazione con il loro valore fisico tramite la rinormalizzazione. Questo

in particolare `e possibile su reticolo quando ci troviamo nella finestra di scaling.

2.2.2

Campi di gauge su reticolo

Nel continuo, per una teoria di gauge si possono definire le matrici [6] p.32 U(s) = L eig

R_s

0 Aµ dxµ, con A_µ = Aa_µT_a, (2.16) dove L sta a indicare il prodotto ordinato, Aa

µ sono i campi di gauge classici,

gli integrali sono di tipo linea e vengono fatti su percorsi xµ(t), con t ∈ [0, 1],

e Ta sono i generatori del gruppo di gauge per cui vale

[Ta, Tb] = ifabcTc, tr(TaTb) =

1 2δab.

Le (2.16) sono elementi del gruppo di gauge. La loro interpretazione fisica `e di essere la fase acquisita da un fermione minimalmente accoppiato con un campo di gauge quando esso percorre la linea definita sui percorsi indicati.

Se a `e sufficientemente piccolo, l’integrale nella (2.16) sul segmento nella direzione positiva µ `e approssimabile con Aµ(x)a. Quindi si possono definire

su reticolo, per campi vettoriali, le quantit`a analoghe alle (2.16) nel modo seguente

Uµ(x) = eigAµ(x)a, (2.17)

definite fra due siti primi vicini fra loro: x `e la coordinata di un sito e µ `e la direzione positiva per raggiungere il sito primo vicino. Le (2.17) sono dette link.

L’analogo delle trasformazioni di gauge dei campi su reticolo pu`o essere definito come

Uµ(x) → V+(x + µ)Uµ(x)V (x),

Si chiama plaquette nella direzione (µ, ν) la quantit`a

Pµν(x) = Uµ(x) Uν(x + µ) Uµ+(x + ν) Uν+(x). (2.18)

Trattandosi di un integrale su un percorso quadrato chiuso, la traccia di Pµν(x) `e un invariante di gauge. Utilizzando la (2.18) definiamo l’azione di

QCD su reticolo nel modo seguente S = βX P ¡ 1 − 1 Nc Re(tr P )¢+ i 2a 3X x,µ ¯ ψ(x)(1 + γµ) Uµ(x) ψ(x + µ) +(a4m + 4a3) X x ¯ ψ(x) ψ(x), (2.19)

dove ψ(x) sono i campi fermionici anticommutanti e la somma degli indici µ `e fatta anche su direzioni negative, per le quali vale

γ−µ= −γµ, U−µ(x) = Uµ+(x − µ).

Le matrici γ soddisfano ora le regole ©

γµ, γν

ª

= −2δµν, γ+

ν = −γν.

La parte fermionica della (2.19) per a → 0 converge effettivamente all’azione sul continuo. Tuttavia, per il noto problema “fermion doubling” l’azione deve essere modificata. Un modo per farlo `e quello di Wilson, che consiste nell’aggiungere il termine correttivo (che per`o rompe la simmetria chirale)

−r 2 X x ¯ ψ(x) ¤ ψ(x),

dove r `e il parametro di Wilson e ¤ `e il laplaciano definito su reticolo. L’hamiltoniana correlata a questa azione fermionica `e chiamata operatore di Wilson-Dirac.

Visto che si deve rispettare il fatto che per a → 0 l’azione discretizzata deve ridursi a quella euclidea sul continuo, ossia che

S = Scont+ O ¡

a6¢_, ne segue che deve valere l’uguaglianza

β = 2Nc g2 .

Quindi i modi possibili di definire l’azione su reticolo sono infiniti. L’unica richiesta `e che nel limite continuo la fisica non dipenda dalla scelta dell’azione. Una volta fissata l’azione, i valori medi degli operatori O(ψ, ¯ψ, U ) si ottengono tramite ­ O®= 1 Z Z Y l dUl Y i

dψid ¯ψie−S(ψ, ¯ψ,U )O(ψ, ¯ψ, U),

dove Z =Z Y l dUl Y i dψid ¯ψi e−S(ψ, ¯ψ,U ),

con l che varia su tutti i link e i che varia su tutti i siti. Gli integrali sui link sono ordinarie integrazioni sul gruppo di gauge, quindi sono fatti su domini compatti. Per gli integrali fermionici la misura `e quella canonica su variabili anticommutanti di Grassman. Entrambe le misure sono invarianti di gauge e quindi anche la misura globale lo `e.

2.3

Relazioni di Ginsparg-Wilson

Per ottenere la relazione di WV anche su reticolo `e fondamentale introdurre un metodo per rappresentare su reticolo la parte fermionica della QCD che preservi le simmetrie chirali.

Il teorema di Nielsen-Ninomiya, noto come no-go theorem, afferma che le seguenti propriet`a, desiderabili in un operatore D di Dirac su reticolo, non possono coesistere:

- D(x) sia locale, cio`e limitato da Ce−γ|x|_,

- D(p) = iγ˜ µpµ+ O(ap2) per p ¿ π/a,

- D(p) sia invertibile per p 6= 0, cio`e che esistano solo fermioni fisici,˜ - γ5D + Dγ5 = 0 (simmetria chirale),

dove ˜D(p) `e la trasformata di Fourier di D(x).

Ne segue che preservare la simmetria chirale su reticolo comporta la perdita di qualche caratteristica fondamentale dell’operatore di Dirac.

Una via di uscita da questa situazione `e fornita dall’operatore di Dirac di overlap, che pu`o essere scritto nella forma

D = 1 ¯a h 1 − γ5² ¡ HW(m) ¢i , (2.20)

dove HW(m) `e l’operatore hermitiano di Wilson-Dirac, ² `e l’operatore segno

e ¯a = a/m.

L’operatore di Dirac in questa forma verifica la relazione di Ginsparg-Wilson (GW)

γ5D + Dγ5 = ¯aDγ5D. (2.21) Il parametro di massa m deve essere scelto nell’intervallo (0, 2) e, nel limite continuo, questa scelta non dovrebbe influenzare la fisica. In pratica, per`o, sia lo spettro di HW(m) sia la localit`a di D dipendono da m [10].

Il fatto che l’operatore di overlap soddisfi le relazioni di Gisparg-Wilson fa s`ı che l’azione nel caso di N quark a massa nulla sia invariante anche sotto la simmetria di singoletto di sapore.