Parametrizzazione del modello SIS di coesistenza competitiva con gruppi di età

Parametrizzazione del modello SIS

di coesistenza competitiva con gruppi di età

In questo capitolo ci preoccupiamo di dare una parametrizzazione più realistica dal punto di vista epidemiologico del modello SIS di coesistenza competitiva formulato e studiato nel paragrafo 5.3.2.

I parametri del modello sono 14, suddividibili in tre categorie: demografici, clinici e di contagio; tale classificazione è riportata nella tabella seguente:

Demografici q, µ1, µ2, b

Clinici γC1, γC2, γL1, γL2

Di contagio a1, a2, βC1, βC2, βL1, βL2

6.1 Parametri demografici

I parametri demografici determinano i valori delle popolazioni di equilibrio e influenzano i parametri derivati che vengono utilizzati per la predizione delle condizioni di equilibrio. Essi possono essere ricavati in modo relativamente semplice da considerazioni intuitive:

q media il flusso di individui dal gruppo 1 al gruppo 2; tale trasferimento è regolato da una

distribuzione di probabilità esponenziale decrescente, tale che la probabilità che un individuo si trovi nel gruppo 1 dopo un tempo t è data da p=e−qt _{; 1/q rappresenta dunque la durata media di} permanenza nel gruppo 1. Poiché vogliamo suddividere la popolazione in modo tale che il primo

gruppo sia esposto prevalentemente alla Neisseria lactamica e il secondo al meningococco, utilizziamo i dati di Coen et al. [1] sulle forze di infezione (FOI) di questi due batteri. Si vede che l'età in cui la FOI del meningococco (curva 3) supera quello della lactamica (curve 1 e 2, a seconda che si consideri la forma di Farrington o quella modificata; v. cap. 4) è attorno ai 10 anni.

Pertanto, supponendo che il primo gruppo comprenda bambini fino a un'età di 1/q = 10 anni, risulta:

q=₁₀1 anni−1=8,33 10−3mesi−1 .

La mortalità infantile µ1 è estremamente bassa e può essere assunta prossima a zero:

1=0 .

µ2 coincide con l'inverso della speranza di vita di un individuo nel comparto degli adulti, che

stimiamo intorno ai 65 anni:

2=

1 65anni

−1

=1,28 10−3mesi−1 .

brappresenta il flusso costante di nascite, che vengono stimate sulle 100.000 all'anno:

b=100.000 anni−1_{=8.333 mesi}−1 Con questi valori si ottengono:

T1 = 1.000.000

T2 = 6.500.000

6.2 Parametri clinici

I parametri clinici riguardano i tassi di guarigione dal carriage, che si possono interpretare come inverso delle durate medie; per determinarli, ci si riferisce agli studi in letteratura.

γC1 e γC2

Apicella [2] cita uno studio in cui si è evidenziata una distribuzione delle durate dei carriage molto irregolare, con un valore mediano intorno ai 9,6 mesi, ma con code di oltre 16 mesi nel 38% dei casi. I modelli di Coen et al. [1] e di Trotter et al. [3] utilizzano dei dati di carriage proposti in due diversi articoli di De Wals nel 1983 e nel 1985 rispettivamente, che suggeriscono nel primo caso una durata di 13,3 mesi, nel secondo di 9 mesi. Taha et al. [4] propongono invece 4.1 mesi.

Schwarz stabilisce per il solo gruppo A una durata molto breve, prossima a un mese, mentre dal modello di Trotter et al. risulterebbe una durata di 3 mesi per il gruppo C, il quale sembra avere una trasmissione più veloce.

Sembra comunque non esserci una forte dipendenza di questa durata dall'età, cosicché stabiliamo che γC1 e γC2 siano uguali e pari a:

C1=C2=

1 9mesi

−1 , come per il modello di Trotter et al.

γL1, γL2

Per la durata media del Neisseria lactamica, lo studio di riferimento sembra per tutti essere quello di Gold et al. del 1978 [5], che stabilisce questo parametro intorno a 3.5 – 4 mesi per bambini di età inferiore agli 8 anni. Non ci sono invece dati sul tasso di guarigione negli adulti. Per questo motivo si considera γL2 come parametro delle simulazioni e si fissa invece il valore di

L1= 1 4mesi −1 .

6.3 Parametri di contagio

Questi due valori indicano il numero di contatti sociali medi di un individio di ciascun gruppo. Secondo dati europei si può stimare il primo in circa 15÷25 contatti al giorno, il secondo in circa 5÷15; scegliamo il valor medio di questi intervalli e riportiamo alle stesse unità di misura degli altri parametri, ottenendo:

a₁=600 mesi−1 _, a₂=300 mesi−1 _. βC1, βC2, βL1, βL2

I parametri di trasmissibilità sono probabilmente i più difficili da stimare, in quanto non facilmente ottenibili da studi sperimentali. Una stima dell'ordine di grandezza può essere ottenuta a partire dall'informazione sull'R0 dell'infezione.

Riscriviamo l'espressione del numero di rimpiazzamento RC ricavata nel par. 5.3.2 in funzione dei 10 parametri di base che interessano questo ceppo (cioè tutti, eccetto i β e i γ relativi alla lactamica):

R_C= a1T1 a1T1a2T2 a₁ C11q C1 a₂T₂ a1T1a2T2 a₂ C22  q C11q a₁T₁ a1T1a2T2 a₂ C22  C2 Definendo: A_C=_a a1T1 1T1a2T2 a₁ C11q B_C= a2T2 a1T1a2T2 a₂ C22  q C11q a₁T₁ a1T1a2T2 a₂ C22 , si ottiene l'espressione: RC=ACC1 BCC2 , da cui: C1= R_C AC – BC AC C2=C−CC2 , con:

C= R_C AC C= B_C A_C .

Analoghe espressioni possono essere ottenute per il gruppo L, sostituendo tutti i pedici C con L. Ipotizzando di conoscere il valore del rapporto

K_C=C2

C1

(e analogamente per il gruppo L), si possono determinare i β attraverso la conoscenza dei valori di RC ed RL: C1= C 1 KCC C2= KCC 1KCC

Ipotizziamo che il valore di tale rapporto possa rientrare entro due ordini di grandezza per entrambi i gruppi, cioè:

10−2_{ K}

C102

10−2_K

L102

.

Secondo il modello di Trotter, RC = 1,36 per il solo serogruppo C del meningococco, perciò si può ragionevolmente supporre che RC relativo a tutti i serogruppi possa essere intorno a 1,5.

Per quanto riguarda Neisseria lactamica, non sono a disposizione dati attendibili, ma vista la maggiore forza di infezione nei primi 10 anni mostrata da Coen et al. (figura 6.1), ci si può aspettare un RL anche sensibilmente più alto. Per il momento comunque anche questo valore rimane un parametro di simulazione.

La tabella seguente mostra un riepilogo dei valori assegnati ai vari parametri, espressi in mesi-1 dove non specificato diversamente.

q µ1 µ2 b γC1 γC2 γL1 γL2 a1 a2 RC* RL* KC* KL* 8,33 10-3 _{0 1,28 10}-3 _{8.333 0,11 0,11 0,25 parametro 600 300 1,5 parametro} >10-2 < 102 >10 -2 < 102 *_{: numeri puri.}

6.4 Parametri di simulazione e condizioni di esistenza

Una volta fissati dei valori più o meno ragionevoli per γL2 e RL, si possono ricavare le regioni dello spazio (KC, KL) per cui è ammessa la coesistenza tra patogeni sulla base delle condizioni ricavate nel paragrafo 5.3.2. Si possono poi rieseguire gli stessi calcoli utilizzando valori diversi di γL2 e RL per valutare il loro effetto sulle condizioni di esistenza.

Inizialmente fissiamo RL = 3 e ammettiamo che il tasso di guarigione da lactamica degli adulti sia identico a quello dei bambini, cioè γL2 = 0,25 mesi-1.

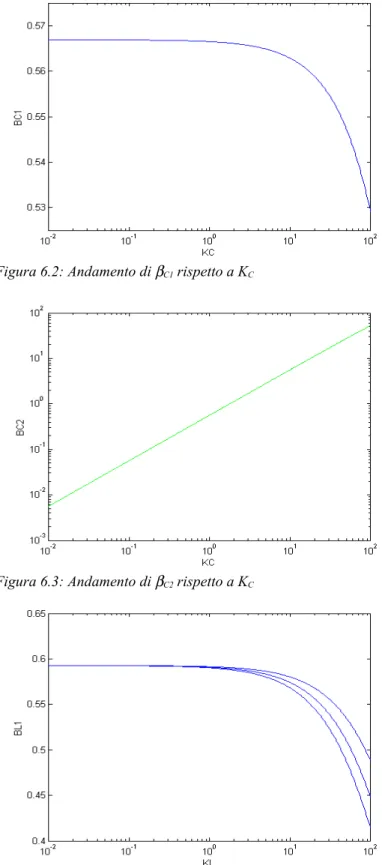
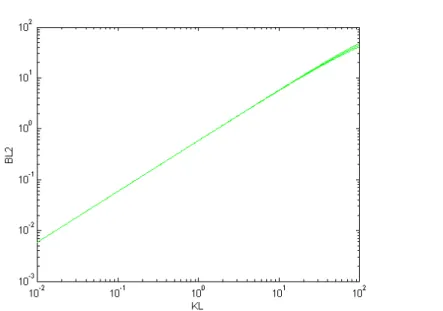
Gli andamenti di βC1 e βC2 con i valori dati al variare di KC sono riportati nelle figure 6.2 (in scala semilogaritmica) e 6.3 (in scala logaritmica). Si nota che l'ordine di grandezza di βC1 rimane praticamente immutato, e che dunque KC fa variare notevolmente solo quello di βC2.

Figura 6.2: Andamento di βC1 rispetto a KC

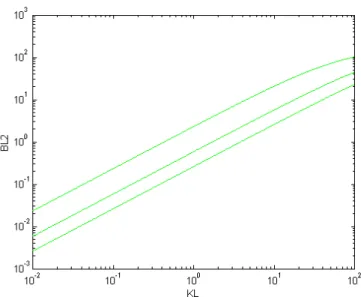
Figura 6.4: Andamento di βL1 rispetto a KL, parametrizzato rispetto a RL = 2, 3 e 4

Per quanto riguarda βL1 e βL2 (figure 6.4 e 6.5), si riportano gli stessi grafici ma calcolati con valori di RL pari a 2, 3 e 4. Le considerazioni sull'influenza di KL sono analoghe a quelle di KC, ma in più si nota che la variazione su valori contenuti di RL non modifica significativamente l'ordine di grandezza dei parametri di trasmissibilità. Possiamo quindi assumere RL = 3 e trascurare le variazioni che esso provoca sui parametri nell'intervallo di KL considerato.

Se invece si fissa il valore di RL e si calcolano i βL al variare di γL2, si ottiene una dipendenza molto più forte, come mostrano i le figure 6.6 e 6.7, in cui le curve sono ottenute con i valori γL2 = 1, 1/4 e 1/9. Una determinazione più precisa della durata del carriage di lactamica negli adulti è quindi necessaria per poter effettuare una parametrizzazione corretta anche dei βL.

Eseguiamo adesso, attraverso un programma in linguaggio Matlab simile a quello usato per determinare i grafici nel paragrafo 5.3.2, il calcolo delle condizioni di coesistenza sulla base delle relazioni determinate nel capitolo precedente. Le regioni che si ottengono questa volta appartengono allo spazio dei parametri (KL, KC) anziché (D1, D2); la scala di riferimento è quella logaritmica.

Figura 6.5: Andamento di βL2 rispetto a KL, parametrizzato rispetto a RL = 2, 3 e 4

Figura 6.7: Andamento di βL2 rispetto a KL, parametrizzato rispetto a γL2 = 1 (curva

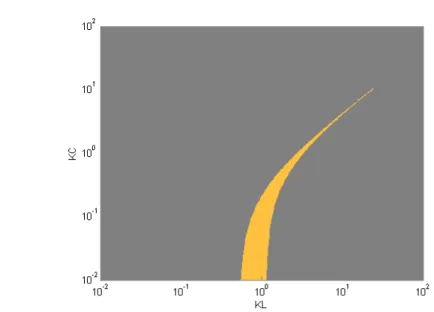
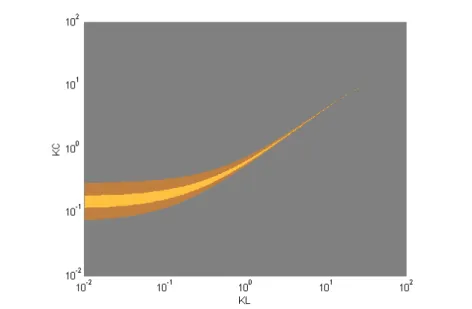
Fissato RL = 3, calcoliamo inizialmente tali regioni nel caso γL2 = γL1 = 1/4: si ottiene (figura 6.8) che le condizioni di coesistenza sono soddisfatte solo in una regione estremamente ristretta dello spazio dei parametri, confinata ad alcuni punti con disposizione regolare.

Se invece si pone γL2 = 1/9 oppure γL2 = 1, si ottengono rispettivamente le regioni di figura 6.9 e 6.10, in cui le condizioni di esistenza occupano una regione di misura non nulla dello spazio (KL, KC).

Figura 6.6: Andamento di βL2 rispetto a KL, parametrizzato rispetto a γL2 = 1 (curva

in alto), 1/4 (centro) e 1/9 (in basso)

6.5 Simulazioni con parametri realistici

Ai valori dei β ottenuti attraverso i valori di K che appartengono la zone di coesistenza dovranno corrispondere degli andamenti delle prevalenze nei due gruppi che all'equilibrio siano diversi da zero per entrambi i tipi batterici; mostriamo che questo avviene attraverso la simulazione dinamica del sistema di equazioni differenziali descrittive del modello effettuata per mezzo della routine di Matlab ode45.

6.5.1 Andamento dinamico al variare di K

e K

Prendiamo come caso base quello descritto nella tabella alla fine del par. 6.3 con RL = 3 e γL2 = 1, ottenendo pertanto le regioni di equilibrio previste dalla figura 6.10. Scegliamo poi quattro punti, mostrati con degli asterischi (figura 6.11) nello spazio (KL, KC), in modo che:

Figura 6.10: Regioni di coesistenza al variare di KC e KL per γL2= 1

• uno sia pienamente all'interno delle regioni di coesistenza (punto A, asterisco nero); • uno sia all'interno di tali regioni, ma prossimo al confine (punto B, asterisco magenta);

• uno sia nella zona in cui la coesistenza è poco stabile rispetto ai valori di KL e KC (punto C, asterisco rosso);

• uno sia all'esterno della regione di coesistenza (punto D, asterisco giallo).

Come condizioni iniziali della simulazione si considera uno stato disease free in cui si introduce un infetto in ciascuno dei due tipi batterici e dei due gruppi di età; la popolazione iniziale è assunta pari a quella di equilibrio, in modo da sopprimere gli effetti legati alla dinamica vitale.

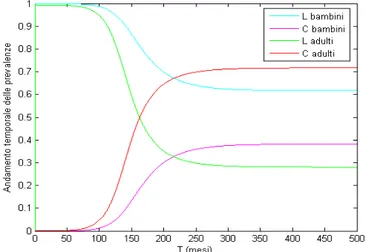
Il punto A rappresenta le coordinate (KL, KC) = (0,01, 0,1565), che individuano i seguenti valori: βC1 = 0,5668;

βC2 = 0,0887; βL1 = 2,3614; βL2 = 0,0236.

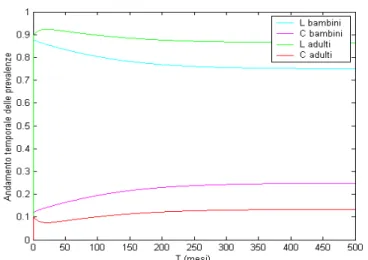
L'andamento delle prevalenze dei vari ceppi nei singoli gruppi è visualizzato in figura 6.12, e mostra due fasi: inizialmente un'ascesa quasi istantanea del gruppo lactamica, legata al maggiore

Figura 6.11: Esempi di coesistenza e di esclusione

Figura 6.12: Andamento dinamico del sistema nel caso base e con KL = 0,01 e KC = 0,1565

valore di RL, a cui fa seguito con un certo ritardo un aumento nella prevalenza del meningococco a spese della lactamica.

Si nota che le scale dei tempi sono molto lunghe (dell'ordine delle decine di anni) e che le prevalenze di equilibrio totali per entrambi i gruppi sono prossime a 1.

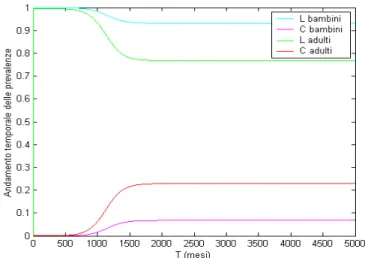
Il punto B corrisponde ai valori KC = KL = 0,1565, da cui βC1 = 0,5668;

βC2 = 0,0887; βL1 = 2,3570; βL2 = 0,3688.

Solo il valore di βL2 è cambiato significativamente rispetto al punto A.

La simulazione mostra (figura 6.13) che si raggiunge l'equilibrio di coesistenza solo dopo un tempo molto più lungo (centinaia di anni) rispetto al caso precedente, a causa dell'aumentata trasmissibilità della lactamica nel gruppo degli adulti, che ritarda ulteriormente l'ascesa del meningococco. Il valore di prevalenza all'equilibrio per quest'ultimo raggiunge valori minori rispetto al caso precedente, come d'altra parte era da aspettarsi, proprio in virtù della maggiore trasmissibilità della lactamica. Anche qui la prevalenza totale all'equilibrio è praticamente del 100%.

Il punto C individua i seguenti valori: KC = 1,2595; KL = 2,4934; βC1 = 0,5664; βC2 = 0,7134; βL1 = 2,2878; βL2 = 5,7044.

Ancora una volta sono solo i β relativi al gruppo 2 a cambiare significativamente ordine di grandezza, ma rispetto ai casi precedenti, entrambi sono maggiori dei β relativi all'età infantile. Anche in questo caso (figura 6.14), il meningococco necessita di molto tempo per poter invadere una popolazione in cui la lactamica è già ben radicata grazie alla sua alta trasmissibilità.

Figura 6.13: Andamento dinamico del sistema nel caso base e con KL = KC = 0,1565

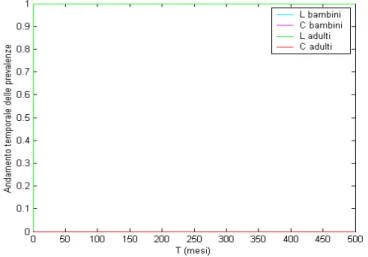
Per il punto D, infine: KC = 0,1565; KL = 2,4934; βC1 = 0,5668; βC2 = 0,0887; βL1 = 2,2878; βL2 = 5,7044.

Il punto non rientra nelle regioni di coesistenza ed in effetti all'equilibrio si ha l'esclusione del meningococco (figura 6.15). Si potrebbe obiettare che i tempi di simulazione sono brevi rispetto ai due esempi precedenti, che nello stesso tempo di 500 mesi mostravano un'esclusione analoga; in realtà, analizzando i valori di prevalenza per t < 500 nei due casi precedenti si vede che i valori sono, seppur minimamente, diversi da zero, e mostrano una tendenza alla crescita. In questo caso il valore previsto è invece identicamente nullo dopo pochi mesi.

Conclusioni sull'effetto di KL e KC

Il punto dello spazio parametrico KL, KC è ovviamente determinante nella dinamica del sistema, in quanto individua i valori dei β che permettono o meno la coesistenza. Esso influenza anche le

Figura 6.15: Andamento dinamico del sistema nel caso base e con KL = 2,4934 e KC = 0,1565

Figura 6.14: Andamento dinamico del sistema nel caso base e con KL = 2,4934 e KC = 1,2595

relazioni nelle prevalenze di equilibrio tra i due agenti infettivi, determinando quale dei due sarà dominante e la rapidità con cui si arriverà all'equilibrio: più si è vicini al confine della zona di coesistenza, maggiore sarà il tempo necessario al batterio meno trasmissibile per invadere una popolazione che il batterio più trasmissibile avrà già colonizzato.

La figura 6.16 mostra in un colore più scuro le sottoregioni all'interno delle zone di coesistenza in cui non si ha l'andamento delle prevalenze di equilibrio effettivamente riscontrato in natura nei due gruppi, cioé L1 > C1 e C2>L2, nel caso base.

6.5.2 Andamento dinamico al variare di

γ

Consideriamo adesso altri valori di γL2 rispetto al caso base, per vedere che effetto ha questo parametro sull'andamento dinamico verso l'equilibrio di coesistenza.

Scegliamo come primo valore γL2 = 1/9, con il quale si ottiene il grafico di figura 6.9, e confrontiamo l'andamento con il punto A del caso base. KL = 1 e KC = 0,01 sono valori che rientrano pienamente nel dominio di esistenza in questo scenario e pertanto li utilizziamo per la simulazione del sistema. Si ottengono:

βC1 = 0,5669; βC2 = 0,0057; βL1 = 0,2647; βL2 = 0,2623.

Il risultato della simulazione è dato dalla figura 6.17, in cui si evidenzia un andamento a regime segnato da tre fasi, ben visibili nell'andamento del meningococco negli adulti: si ha una ascesa molto rapida, a cui fa seguito un calo temporaneo della prevalenza, e una nuova ascesa monotona verso il valore di equilibrio. La durata del transitorio è ancora dell'ordine delle decine di anni, come nel punto A del caso base. Ci si potrebbe chiedere se le tre fasi non siano un'indizio per delle oscillazioni rapidamente smorzate; analizzando lo spazio delle fasi relativo al solo gruppo degli adulti si vede che non ci sono andamenti spiraleggianti, ma piuttosto due cuspidi; d'altra parte gli autovalori dello jacobiano intorno al punto di equilibrio sono tutti reali nelle zone di coesistenza calcolate.

Figura 6.16: Regioni di coesistenza al variare di KC e KL per γL2 = 1; il

Vediamo adesso il comportamento del sistema quando si prendono valori estremi di γL2, per valutare la possibilità che insorgano dei comportamenti oscillatori. Prendiamo dunque i valori γL2 = 1/100 e γL2 = 1/0,1 = 10 e ci poniamo in un punto della regione di coesistenza per valutare l'andamento dinamico.

Nel primo caso (figura 6.18) si ottiene, per KL = 1, KC = 10-2: βC1 = 0,5669;

βC2 = 0,0057; βL1 = 0,0266; βL2 = 0,0264.

Nel secondo (figura 6.19) scegliamo KL=0,1565 e KC = 1, da cui risulta: βC1 = 0,5665;

βC2 = 0,5665; βL1 = 23,1218; βL2 = 3,6175.

Figura 6.17: Andamento dinamico del sistema con γL2 = 1/9, KL = 1 e KC = 0,01

Figura 6.18: Andamento dinamico del sistema con γL2 = 1/100, KL = 1 e KC = 0,01

La durata del transitorio è in questo caso notevolmente più breve (pochi anni), grazie al fatto che la guarigione rapida dalla lactamica permette ai meningococchi di invadere in fretta il gruppo degli adulti, ed in seguito anche quello dei bambini, seppure in misura minore.

Conclusioni sull'effetto di γL2

γL2 è l'unico parametro epidemiologico totalmente ignoto che influisca pesantemente sulla dinamica del sistema. Si è appurato che, sotto l'ipotesi di γC1 = γC2, esso non può essere uguale a γL1, altrimenti non esistono zone di coesistenza. Al variare di questo parametro, le regioni di coesistenza per i parametri di trasmissibilità, mediate dai valori di K si modificano pesantemente, estendendosi per valori estremamente piccoli o estremamente grandi. La dinamica con cui il sistema va a regime sembra non mostrare comportamenti oscillatori per nessun valore di γL2; esso influisce sulla forma dell'andamento temporale della prevalenza (v. figura 6.17) e sulla durata del transitorio.

Riferimenti bibliografici

[1] Coen P. G., Cartwright K., Stuart J. (2000) Mathematical modelling of infection and disease due to Neisseria meningitidis and Neisseria lactamica. International Journal of

Epidemiology 29, 180–188.

[2] Apicella M. A. Neisseria meningitidis. In Infectious Diseases and Their Etiologic Agents, 2498-2508.

[3] Trotter C. L., Gay N. J., Edmunds W. J. (2005) Dynamic Models of Meningococcal Carriage, Disease, and the Impact of Serogroup C Conjugate Vaccination. American

Journal of Epidemiology, 162, 89-100.

[4] Taha M. K., Deghmane A. E., Antignac A., Zarantonelli M. L., Larribe M., Alonso J. M. (2002) The duality of virulence and transmissibility in Neisseria meningitidis. Trends in

Microbiology, 10, 376-382.

[5] Gold R, Goldschneider I, Lepow ML, Draper TF, Randolph M. (1978) Carriage of Neisseria meningitidis and Neisseria lactamica in infants and children. J Infect Dis,

137(2), 112-21.

Figura 6.19: Andamento dinamico del sistema con γL2 = 10, KL = 0,1565 e KC = 1