1. Dinamica del veicolo

1. Dinamica del veicolo

Per poter implementare un controllo automatico, in primis si deve formarsi una conoscenza del sistema fisico da controllare, capirne le problematiche e formularne un modello matematico che ne descriva le caratteristiche dinamiche nel modo più completo ed esauriente possibile. Nel nostro caso il sistema fisico da controllare sarà un veicolo stradale con due soli assali e quattro ruote dotate di pneumatici; in particolare, eseguiremo le varie ipotesi considerando che i risultati siano il più possibile confrontabili con quelli reali ottenuti da una normale vettura da turismo di serie. Vedremo come certe ipotesi semplificative e certe modellazioni che trascurano le non linearità intrinseche si adattino in realtà meglio a vetture di classe sportiva o da competizione, ed è per questo che non potremo fare a meno di considerare nel nostro studio le numerose non linearità di modello.

La dinamica del veicolo stradale è una materia in cui teoria ed esperienza sono ugualmente importanti, ma raramente senza un accorto impiego di modelli matematici se ne riesce ad acquisire una conoscenza organica. La tentazione iniziale può essere quella di creare un modello molto accurato, nella speranza di poter descrivere tutti i fenomeni dinamici che intervengono durante il moto del veicolo stesso. Purtroppo modelli troppo complicati diventano non gestibili sia dal punto di vista della formulazione matematica che della gestione dei risultati; inoltre coinvolgono molti parametri difficilmente rilevabili con precisione e quindi portano ad una accuratezza solo fittizia del modello utilizzato. E’ bene allora prendere in esame modelli relativamente molto semplici e classici, con pochissimi gradi di libertà, che permettono comunque di

descrivere gli aspetti salienti del moto del veicolo, anche se solo in particolari condizioni di impiego.

1.1 Ipotesi semplificative

Dovendo realizzare un modello molto semplice ma comunque valido nell’analisi delle problematiche di guida, riveste notevole importanza la scelta delle ipotesi semplificative da effettuare sul caso reale e la loro influenza sull’analisi matematica eseguita.

Nella formulazione dei nostri modelli considereremo quindi che: - il veicolo sia un corpo perfettamente rigido

- il veicolo si muova su strada piana e orizzontale, assimilabile cioè ad un piano geometrico

- non esista nessun sistema di sospensioni

- la velocità di avanzamento abbia variazioni piccole e lente, cosa che ci permetterà di trascurare l’influenza sul moto di eventuali moti di beccheggio e di scuotimento e gli scorrimenti laterali dei pneumatici

- le curve siano ad ampio raggio e percorse a bassa velocità, così da poter ritenere trascurabile il moto di rollio e, di conseguenza, le variazioni degli angoli di Camber delle ruote. Si noti inoltre che avendo reso trascurabili le rotazioni del veicolo attorno agli assi di riferimento, il moto dello stesso può essere ritenuto piano.

- il sistema di guida sia perfettamente rigido, quindi il valore dell’angolo δ di sterzata delle ruote è univocamente determinato dalla posizione dello sterzo.

- le ruote anteriori abbiano massa molto inferiore rispetto al resto

del veicolo, quindi la loro posizione non modificherà la posizione del

baricentro del sistema.

- l’asse di sterzo di ciascuna ruota anteriore sia assimilato ad un asse verticale di strada.

- gli angoli di sterzo siano piccoli, cosa che ben si concilia con l’ipotesi precedente di curve ad ampio raggio.

L’effetto totale di tutte queste ipotesi è un modello a tre soli gradi di

libertà, in cui il veicolo è schematizzato come un unico corpo rigido in

moto piano.

Si noti che, abbastanza paradossalmente, il modello proposto si presta meglio allo studio del comportamento di un’automobile da corsa che non di una tranquilla vettura da turismo.

Vedremo successivamente come la rimozione di alcune delle ipotesi precedenti porti ad una notevole complicazione del modello.

1.2 Dal veicolo al modello matematico

Sulla base delle precedenti ipotesi, si procede a formulare un modello di autoveicolo.

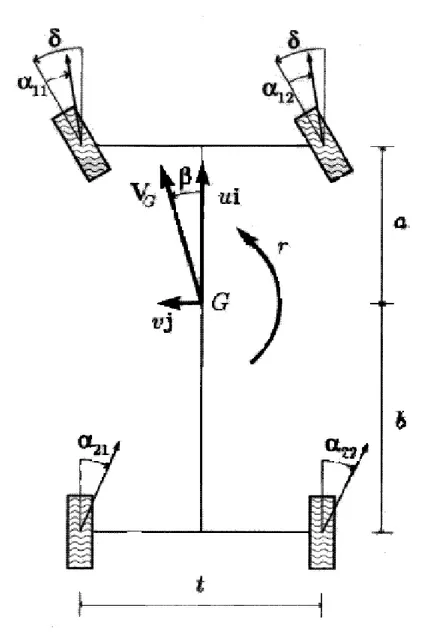
Un possibile schema è rappresentato in Fig. 1.1. Si tratta di un unico corpo rigido di massa m e baricentro G. In realtà il veicolo dispone di due ruote anteriori sterzanti, ma, come si è già detto, si assume che la loro massa sia così piccola da non influenzare la posizione del baricentro.

Fig. 1.1: Modello di veicolo a tre gradi di libertà

Si definisce un sistema di riferimento cartesiano (x,y,z;G) solidale al veicolo, e quindi solitamente detto “assi corpo”, con origine nel baricentro. L’asse x viene assunto parallelo alla strada e diretto secondo il verso di avanzamento del veicolo, l’asse z ortogonale alla strada e diretto verso l’alto e l’asse y perpendicolare agli altri due e diretto verso il centro della curva.

In generale questo sistema di riferimento non coincide con la terna centrale di inerzia. Se però si assume che il veicolo sia simmetrico

rispetto al piano longitudinale contenente i due assi x e z, almeno l’asse y è di inerzia e quindi si annullano i prodotti d’inerzia Jxy e Jyz, mentre è in

generale non nullo il prodotto d’inerzia Jzx (stimabile nelle automobili in

200 Kg m2). Sono ovviamente sempre non nulli i tre momenti d’inerzia

Jx, Jy e Jz.

Come già detto, il veicolo è supposto in moto piano. Si indica con Ω = r

k la sua velocità di imbardata (yaw rate), con k ortogonale al piano

stradale e diretto verso l’alto. Pertanto, r è positiva se il corpo ruota in senso antiorario. La velocità assoluta del baricentro è indicata con VG.

La posizione del baricentro rispetto al veicolo è definita dalle lunghezze

a e b (dette semipassi). Con l = a + b e t si indicano, rispettivamente. il

passo (wheelbase) e la carreggiata (track) del veicolo, entrambe misurate dai centri delle ruote. Carreggiata anteriore e posteriore sono supposte uguali.

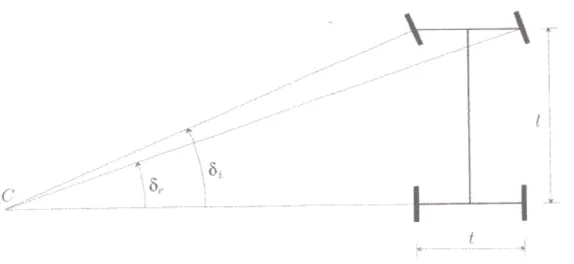
Per la cosiddetta sterzata cinematica, cioè con angoli di deriva tutti nulli come illustrato in Fig.1.2 , l’angolo di sterzo δi della ruota interna

alla curva deve essere ovviamente maggiore di quello della ruota esterna δe secondo la relazione: ) tan( 1 e) tan( 1 i l t δ δ − = (1.1) da cui si ricava ) ( 3 2 i i O l t i e δ δ δ δ = − +

Fig. 1.2: Sterzata cinematica, ossia con angoli di deriva nulli

Per piccoli angoli di sterzo, si ha δi ≈ δe. Per questo motivo, indicheremo

entrambi con δ (Fig. 1.2).

Si può ora procedere alla formulazione matematica del modello mediante i seguenti tre gruppi di equazioni, fra loro ben distinti: equazioni di

1.3 Equazioni di congruenza

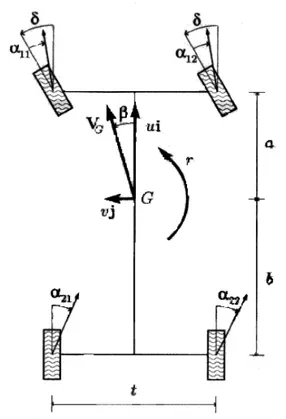
Fig. 1.3: Definizione delle grandezze cinematiche nel modello del veicolo

L’angolo di deriva α individua la direzione della velocità del centro ruota rispetto al piano di simmetria longitudinale della ruota stessa. Esso viene qui assunto positivo se diretto in senso orario. Avendo schematizzato il veicolo come corpo rigido, la velocità del baricentro VG

e la velocità di imbardata r determinano univocamente gli angoli di deriva αij delle quattro ruote (i=1,2; j=1,2).

Si ha (Fig. 1.3) VG = (u,v,0), ovvero

VG = ui+vj (1.2)

La componente u è detta velocità di avanzamento mentre la componente v è detta velocità laterale del veicolo. Per costruzione il baricentro è fermo rispetto al sistema di riferimento solidale al veicolo,

quindi la (1.2) non esprime la velocità del baricentro rispetto a questo riferimento ma solo le componenti della velocità assoluta di G in direzione longitudinale e trasversale al veicolo.

L’angolo β = arctan(v/u) fra asse longitudinale del veicolo e la direzione della velocità VG del baricentro viene detto angolo di assetto del veicolo

(vehicle attitude o più propriamente slip angle).

Grazie alle ipotesi fatte precedentemente, nel sistema di riferimento prescelto la velocità angolare del veicolo ha due componenti nulle:

Ω = (0,0,r). Si ha cioè solo imbardata, senza beccheggio e rollio. Si

considerino le velocità assolute dei centri delle ruote al fine di legare gli

angoli di deriva alla velocità di imbardata r e alle componenti u e v

nelle equazioni di congruenza. I centri di entrambe le ruote anteriori hanno velocità in senso trasversale pari a v+ra, così come quelli delle ruote posteriori hanno una velocità trasversale pari a v-rb. In senso longitudinale, i centri delle due ruote sul fianco sinistro hanno velocità pari a u-rt/2, mentre quelli delle ruote sul fianco destro hanno velocità pari a u+rt/2. Ne seguono subito le seguenti relazioni rigorose, in cui le prime due sono relative alle ruote anteriori e le altre alle ruote posteriori:

2 / ) tan( ₁₁ rt u ra v − + = −α δ 2 / ) tan( ₁₂ rt u ra v + + = −α δ (1.3) 2 / ) tan( ₂₁ rt u rb v − − = −α 2 / ) tan( ₂₂ rt u rb v + − = −α

Se si tiene conto che in normali condizioni di esercizio u >> rt/2, si

lavorano con angoli di deriva quasi uguali. Si può quindi indicare con α1

l’angolo di deriva di entrambe le ruote anteriori e con α2 l’angolo di

deriva delle ruote posteriori. Le precedenti relazioni si riducono così a due: u ra v+ = − ) tan(δ α₁ (1.4) u rb v− = − ) tan(δ α₂

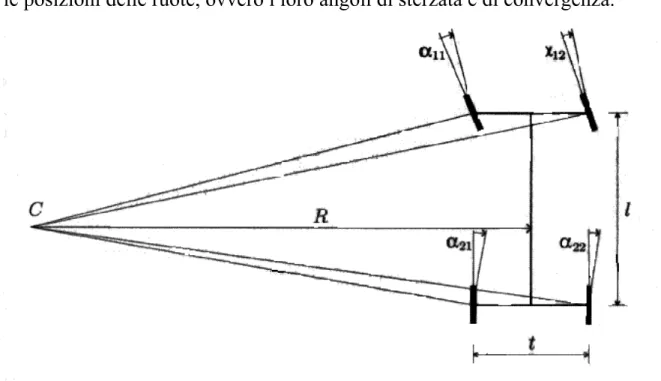
Come abbiamo già detto a proposito della sterzata cinematica, nella realtà in condizioni di normale funzionamento l’angolo di deriva della ruota esterna alla curva è lievemente inferiore a quello della ruota interna. Come mostrato in Fig. 1.4, la posizione del centro di istantanea rotazione definisce univocamente tutti gli angoli di deriva, note che siano le posizioni delle ruote, ovvero i loro angoli di sterzata e di convergenza.

Fig. 1.4: Relazione fra gli angoli di deriva delle quattro ruote e la posizione del centro di istantanea rotazione C.

Per semplificare ulteriormente, si può considerare il fatto che la velocità di avanzamento u è, di norma, ben più elevata della velocità laterale v e

delle velocità dovute alla presenza di r. Si ha cioè che u>> v+ra e

rb v

u >> − . E’ quindi legittimo nelle (1.4) confondere l’arco con la tangente ed ottenere le seguenti equazioni di congruenza linearizzate

u ra v+ = −α₁ δ (1.5) u rb v− = −α₂

che legano le velocità u, v, r agli angoli di deriva α1 e α2.

Se valgono le stesse ipotesi, anche l’angolo di assetto β = arctan (v/u) di Fig.1.3 può essere valutato mediante una relazione linearizzata

u v =

β (1.6)

Si ricorda che, mentre le (1.3) valgono sempre, anche durante un testa coda, le (1.5) e le (1.6) possono essere utilizzate solo quando c’è preponderanza di u rispetto a tutte le altre velocità. A meno che non venga espressamente dichiarato il contrario, da questo punto in poi si dà per scontato di trovarsi in condizioni normali di funzionamento, con questa ipotesi perfettamente verificata.

Sottraendo membro a membro le due equazioni di congruenza (1.5) si ottiene l’importante relazione cinematica

2 1 2 1 ) ( α α α α δ = + + − = + − R l u r b a (1.7)

dove si è introdotta la lunghezza (con segno) R=u/r.

Essendo stata ottenuta direttamente dalle (1.5) la relazione (1.7) vale anche in condizioni non stazionarie. La lunghezza R rappresenta semplicemente la distanza del centro di istantanea rotazione C dall’asse del veicolo (Fig.1.4). Il punto sull’asse ottenuto portando la perpendicolare da C ha infatti velocità laterale nulla e velocità assoluta

pari ad u. La lunghezza R è positiva se C si trova sulla sinistra del veicolo (r>0), come in Fig. 1.4.

Per meglio chiarirne il significato applicativo, la condizione

2 /

t r

u >> utilizzata in precedenza può essere riscritta come rR >> rt/2, ovvero come R >>t/2.

Le equazioni di congruenza (1.5) possono anche essere espresse in una forma alternativa utilizzando le definizioni di β e di R, ricavando facilmente la relazione seguente:

] ) ( [ 1 2 1 α α δ β b a l − − = (1.8)

Si noti anche che in generale βR = v/r.

Si parla di condizioni stazionarie di funzionamento se le grandezze in gioco (u, v, r, δ e quindi anche α1 e α2) rimangono costanti nel tempo. In

questo caso, tutti i punti del veicolo percorrono traiettorie circolari con centro C, che rimane fisso avendo, oltre alla velocità, anche accelerazione nulla. Si tratta della cosiddetta manovra di “steering pad”. In queste e sole particolari condizioni di funzionamento, di cui verificheremo più avanti l’importanza, la distanza R rappresenta anche il raggio di curvatura della traiettoria di quel punto sull’asse del veicolo che ha la minima distanza da C.

La quantità δ0 = l/R è detta angolo di Ackermann, e rappresenta

l’angolo di sterzo per percorrere una curva di raggio costante pari ad R, supponendo di avere angoli di deriva nulli (la già vista sterzata cinematica).

1.4 Equazioni di equilibrio

La stesura delle equazioni di equilibrio richiede due distinte operazioni: il calcolo delle accelerazioni e la valutazione delle forze e dei momenti agenti.

1.4.1 Calcolo delle accelerazioni

L’espressione dell’accelerazione aG del baricentro si ottiene

immediatamente derivando rispetto al tempo la velocità VG = ui + vj.

Naturalmente, occorre tenere in considerazione la variazione della direzione dei versori durante il moto per cui di/dt = rj e dj/dt = -ri. Pertanto si ha j i j ) ( i ) ( i j j i V a G _{x y} G _dt u ur v vr u vr v ur a a d _{= + + − = − + + = +}

= _{& & & &} (1.9)

In questo modo si è scomposta aG in accelerazione longitudinale

vr u a_x = &− (1.10) e in accelerazione laterale R u v ur v a_y 2 + = + = _{& &} (1.11) rispetto all’asse del veicolo.

Si rivelerà importante l’aver definito l’accelerazione laterale a regime come R u ur a_y 2 ~ _{= = (1.12)} così da avere a_y = &v+a~_y

Se si rapporta a~_yalla accelerazione di gravità g si ottiene

g a

k ₌~y _(1.13)

il cui valore massimo è detto tenuta in curva.

Se si considera che la traiettoria del baricentro G è sempre tangente a VG,

si può scomporre aG anche in accelerazione normale o centripeta an e in

accelerazione tangenziale at. Più precisamente si ha

aG = att + ann

dove si sono usati i versori t = (cosβ,sinβ) e n = (-sinβ, cosβ), parallelo e normale a VG. Si noti che per portare t su n è necessaria una rotazione

antioraria di 90°.

Le due componenti sono date da

at = aG. t = axcosβ + aysinβ = _{2 2} v u v v u u + + & & _(1.14) e an = aG. n = -axsinβ + aycosβ = 2 2 2 2 ₎ ( v u u v v u v u r + + − + _{& & (1.15)} dove si è tenuto conto che sinβ = v/VG e cosβ = u/VG.

A questo punto è immediato ricavarsi anche l’espressione generale del

raggio di curvatura RG della traiettoria di G

2 2 2 2 2 3 2 2 2 ) ( ) ( G G G n G G V u v V v u r V u v v u v u r v u a V R & & & & + = _{− +} − + + = = (1.16)

Si tratta di una quantità con segno: RG è positivo se il centro di curvatura

si trova sulla sinistra del veicolo, negativo in caso contrario.

Si può assumere u , poiché nella maggioranza delle manovre standard

l’accelerazione longitudinale è sempre molto bassa. Considerando poi che u/V

0 ≡ &

raggio di curvatura della traiettoria del baricentro, valida anche in condizioni di moto vario

u v r u V v r V R G G G _{& &} + ≈ + ≈ (1.17)

Come si vede, la presenza di può rendere Rv& G ben diverso da R = u/r. Si

noti inoltre che r& non compare nell’espressione di RG.

Nel caso di moto in condizioni stazionarie, ovvero con , l’accelerazione di G è solo centripeta, ovvero a

0 = = v

u_{& &}

t = 0 e an = VGr. Rispetto

al riferimento (x,y,z;G) solidale al veicolo, inclinato dell’angolo di assetto β rispetto alla traiettoria di G, si hanno a regime ax = -vr e ay = ur

= u2/R.

Per concludere il calcolo delle accelerazioni non rimane da considerare che l’accelerazione angolare: essa è data banalmente da Ω& =(0,0,r&).

1.4.2 Forze e momenti

In generale su un qualsiasi veicolo terrestre, in particolar modo su un autoveicolo, agiscono tre tipi di forze: la forza peso dovuta alla gravità, le reazioni sulle quattro ruote dovute al contatto pneumatico-strada e le

forze aerodinamiche dovute alla presenza dell’aria.

Rispetto al sistema di riferimento di assi corpo (x,y,z;G), si indicano con

(X,Y,Z) le tre componenti della forza risultante agente globalmente sul

veicolo e con (L,M,N) le sue tre componenti di momento.

Le tre equazioni di equilibrio dell’unico corpo rigido in moto piano (come abbiamo schematizzato il nostro autoveicolo grazie alle ipotesi semplificative), di massa m e momento d’inerzia J = Jz rispetto all’asse

verticale z per G, si possono quindi indicare sinteticamente nel modo seguente m ax = X (1.18) m ay = Y J r& = N

Fig.1.5: Forze agenti sul modello di veicolo

Una prima possibile complicazione del modello per renderlo più affine alla realtà sarebbe l’utilizzo nella prima equazione in (1.18) della massa apparente traslante mat che tiene conto anche dell’inerzia delle masse in

moto rispetto alla cassa del veicolo (ruote, motore, ecc.) in base alla seguente relazione 2 2 1 u m T = _at (1.19)

in cui T indica l’energia cinetica globale del veicolo. Tuttavia, si può verificare sperimentalmente come nelle marce lunghe mat sia di poco

superiore ad m, mentre in prima marcia la massa apparente traslante può essere anche il doppio di m, soprattutto a causa dell’inerzia e della notevole velocità di rotazione del motore. Dato che gli studi sulla guidabilità riguardano velocità di avanzamento abbastanza elevate, ottenibili solo con marce lunghe, è lecito utilizzare m anche nella prima equazione [17, 18].

Nell’ambito del modello piano in esame, le principali forze agenti sul

veicolo sono le forze trasmesse dai pneumatici, come indicato in

Fig.1.5, che servirà anche a definire le direzioni positive delle singole componenti delle forze. A queste si possono aggiungere la resistenza aerodinamica e l’eventuale spinta laterale del vento, di cui verificheremo la notevole influenza sui parametri di guida.

Si indicano con Fxij le componenti longitudinali e con Fyij le componenti

trasversali delle forze trasmesse dalla strada alle quattro ruote, dove i termini longitudinale e trasversale sono qui relativi alla ruota e non al veicolo. Per semplicità si suppongono nulli tutti i momenti di

autoallineamento Mzij.(A proposito delle forze agenti sui pneumatici e

sul loro rapporto si veda per approfondimento [6, 17, 18, 20]). Lo spostamento di pochi centimetri della retta di applicazione delle forze laterali avrebbe ben poca influenza sulla dinamica globale del veicolo.

Nelle Fxij vengono inglobate le forze di trazione e le resistenze al

rotolamento, anche se queste ultime sono spesso di entità trascurabile durante il moto in curva.

Tenendo conto che per angoli di sterzo fino a circa 15° è lecito porre cosδ ≈ 1 e sin δ ≈ δ, si ottiene dalla Fig. 1.5

2 2 1 ) ( ) ( ) ( ) ( 22 21 12 11 12 11 F F F F F SC u F vr u m _&− = _x + _x − _y + _y δ + _x + _x − ρ _x (1.20) ) ( ) ( ) ( ) ( 22 21 12 11 12 11 x y y y y x F F F F F F ur v m _&+ = + δ + + + + 2 ] ) ( ) ( ) [( ) ( )] ( ) [( 12 11 22 21 12 11 22 21 12 11 12 11 t F F F F F F b F F a F F F F r J_&= _x + _x δ + _y + _y − _y + _y − _x − _x + _x − _x − _y − _y δ

Si può avere una notevole semplificazione sommando i contributi delle due ruote di uno stesso asse ponendo

12 11 1 x x x F F F = + 22 21 2 x x x F F F = + (1.21) 12 11 1 y y y F F F = + 22 21 2 y y y F F F = +

in modo da rendere più compatta la notazione.

Nel caso della ripartizione della coppia motrice fra le due ruote dello stesso asse avvenga mediante un differenziale ordinario (non autobloccante), si ha che Fx11 = Fx12 e Fx21 = Fx22, con il conseguente

annullamento di parte dell’ultima riga in (1.20).

Rimane però il termine con (Fy11-Fy12)δt/2, che dal momento che contiene

la differenza delle forze laterali delle due ruote anteriori, costituisce un termine alquanto fastidioso per i successivi sviluppi. E’ prassi comune trascurare questo termine [7]. Si potrebbe anche ritenere che Fy11 ≈ Fy12,

ma, come evidenziato nella formulazione delle equazioni costitutive (1.3) e (1.4), anche se le due ruote lavorano con angoli di deriva quasi

uguali questo non basta per avere forze laterali quasi uguali. Anzi, a causa del trasferimento di carico, le due ruote sono sottoposte in curva a carichi verticali Fzij diversi e ciò ha una certa influenza. In definitiva,

l’eliminazione dell’ultimo termine in (1.20) limiterebbe l’uso del modello a manovre con piccole accelerazioni laterali, anche se questo requisito viene spesso disatteso nella pratica corrente.

In base a quanto detto, si possono scrivere le equazioni di equilibrio nella seguente forma

2 2 1 ) (u vr F₁ F₂ F₂ SC u m _&− = _x − _yδ + _x − ρ _x 2 1 1 ) (v ur F_x F_y F_y m _&+ = δ+ + (1.22) b F a F F r J&=( _x1δ + _y1) − _y2

in cui compaiono le componenti longitudinali e laterali delle forze esercitate globalmente da ciascun assale.

1.5 Equazioni costitutive

Per completare il modello del veicolo resta da definire il comportamento di ciascun pneumatico. Dalla notevole bibliografia presente sull’argomento, emerge che la forza laterale Fyij, esercitata dalla strada su

ciascuna ruota, dipende principalmente dal corrispondente angolo di deriva αij, ma non solo. Anche supponendo noto il coefficiente di

aderenza, si ha una influenza non trascurabile del carico verticale Fzij ed

anche dell’angolo di campanatura (camber) γij e della forza longitudinale

Fxij.

Tener conto di tutti questi fattori non è facile e non esiste una soluzione ottimale, ma vari compromessi fra semplicità e completezza, che

originano modelli matematici diversi. Si tenga sempre presente che ogni modello ha dei limiti e che nessuno è necessariamente migliore degli altri.

Per quanto riguarda l’influenza dell’angolo di camber, c’è da dire che la presunta trascurabilità del moto di rollio rende trascurabili anche le variazioni dell’angolo di camber delle singole ruote. Dato che, in marcia rettilinea, le due ruote di un assale hanno angoli opposti (γi1 = -γi2), si ha

l’annullamento reciproco della spinta di camber quando si considera la somma Fyi delle forze laterali agenti sulle ruote di uno stesso assale.

Con queste premesse, vengono solitamente formulati tre modelli di pneumatico, che qui accenneremo brevemente.

2.5.1 Pneumatico linearizzato

Ipotizza un legame lineare fra forza laterale e angolo di deriva. E’ il modello più semplice.

ij yij C ij

F = _αα

da cui, grazie al fatto che αi1 = αi2, è immediato ottenere

i yi C i C i F ( _{α α} )α 2 1+ =

Il campo di impiego è limitato a quei casi in cui gli angoli di deriva non superano i 2° su strada asciutta. Su strada scivolosa il campo lineare è ancor più limitato.

1.5.2 Pneumatico linearizzato con ritardo di risposta

Il modello lineare ipotizza una risposta immediata del pneumatico all’angolo di deriva. Se si vuole introdurre un ritardo di risposta pur

mantenendo il modello lineare, si può applicare la seguente

) (t C F F u d i i y yi + i = α &

dove d è la lunghezza di rilassamento di ciascuna ruota. Si noti che il pneumatico linearizzato senza ritardo può essere considerato un caso particolare di questo con d→0. Anche in questo caso le rigidezze di deriva Ci sono supposte costanti durante il moto.

1.5.3 Pneumatico non lineare

Se si vogliono studiare situazioni in cui gli angoli di deriva possono raggiungere valori elevati non è più possibile ipotizzare un legame lineare. Occorre introdurre l’effettiva risposta non lineare del pneumatico all’angolo di deriva, magari utilizzando una formula empirica tipo la Magic Formula oppure una tabella con rilevamenti

sperimentali.

In definitiva, una volta stabilito il fondo stradale e quindi il corrispondente coefficiente di aderenza, si suppone di conoscere per ciascun pneumatico una funzione del tipo

) , ( ij ij i i z y f F F = α

Ovviamente i carichi verticali Fzij agenti sulle singole ruote sono variabili

durante il moto. Inoltre, non possono essere determinati con semplici condizioni di equilibrio, ma solo considerando le sospensioni elastiche.

Nei veicoli senza sospensioni, come quello in esame, la cosa si presenta quindi problematica.

Fortunatamente è possibile, mediante un procedimento approssimato, far dipendere il carico verticale su ciascuna ruota di un assale dal corrispondente angolo di deriva. In tal modo, la forza laterale esercitata da ciascun assale può essere espressa come una funzione non lineare del solo angolo di deriva secondo la relazione

)) ( , ( )) ( , ( _{i z1 i i i z2 i} i yi f Fi f Fi F = α α + α α .

Introducendo una notazione più sintetica si ha quindi il legame ) ( _i i y Y F i = α

dove la funzione Yi(αi) è detta caratteristica effettiva dell’assale.

Volendo si può introdurre un ritardo di risposta anche per pneumatici non lineari, procedendo come visto nel § 1.5.2.