Juniode2006 JulioD.PérezTudela Análisisdelainfluenciadelasaberracionesdelsistemadifractorenelreconocimientodeimágenesporcorrelaciónóptica GrupdeRecercaenÒpticaF´ısicaDepartamentdeF´ısicaAplicadaiÒpticaUniversitatdeBarcelona

(1)

Departament de F´ısica Aplicada i `Optica Universitat de Barcelona

An´

alisis de la influencia de las aberraciones del sistema

difractor en el reconocimiento de im´

agenes por

correlaci´

on ´

optica

Julio D. P´erez Tudela

(2)

Correlador convergente de

Vander Lugt

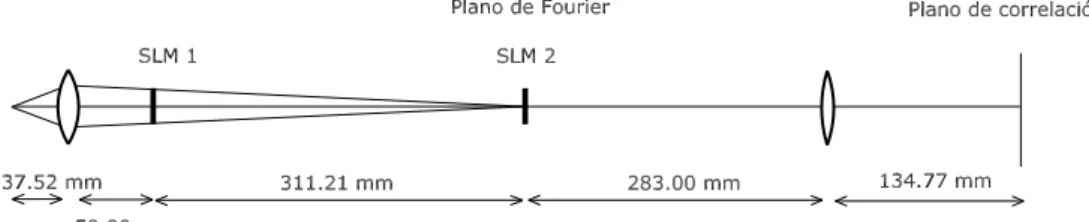
En el apartado 1.4.2 se introdujo una de las arquitecturas básicas utilizadas en la correlación óptica: el correlador de Vander Lugt. El primer montaje propuesto por el propio Vander Lugt fue el denominado correlador 4f [Lug64], el cual recibe este nombre por la distancia existente entre el plano de entrada y el de correlación. Un esquema de este dispositivo se puede ver en la figura 1.2. Tal y como se comentó en dicho apartado, uno de los principales inconvenientes que presenta esta configura-ción es la longitud necesaria para obtener las imágenes escaladas de forma adecuada, as´ı como la dificultad para adaptar la escala de la transformada de la escena a la del filtro utilizado. De las diferentes modificaciones que se han ido proponiendo la más utilizada es el denominado correlador convergente de Vander Lugt (ver figura 5.1), el cual se basa en el acoplamiento de dos difractómetros mediante la utilización de lentes convergentes.

Generalmente, la imagen a analizar es proyectada en una pantalla LCD situada en el plano de entrada. En el plano de Fourier se sitúa un segundo modulador que es el encargado de mostrar los filtros donde se encuentra codificada la imagen a detectar. Finalmente, los resultados de la correlación son capturados por una cámara de video CCD situada en el plano de correlación.

En este cap´ıtulo se pretenden analizar diversos aspectos de la influencia en la corre-lación de las aberraciones de los sistemas ópticos que componen el correlador con-vergente de Vander Lugt, y se propondrán diversos métodos para minimizar estos

(3)

efectos. En primer lugar, y continuando con la l´ınea desarrollada en el cap´ıtulo ante-rior, se evaluará la influencia de las aberraciones de cada uno de los difractómetros en la correlación final. A partir del análisis de los resultados obtenidos, se inten-tará reducir esta influencia mediante dos procedimientos: por una parte, modificando la posición relativa de los moduladores respecto de los sistemas ópticos, mantenien-do constante la distancia entre ellos. Por otro lamantenien-do, se generarán filtros a partir de imágenes afectadas por aberración, y se compararán los picos de correlación con los iniciales. Finalmente, se sintetizará este conjunto de medidas en la propuesta de un diseño óptimo para el correlador analizado.

5.1. Proceso de correlaci´

on en el correlador de Vander

Lugt

Como ya hemos dicho anteriormente, las principales ventajas que presenta la arqui-tectura de Vander Lugt respecto del correlador 4f son, por un lado, la reducción de la longitud total del sistema, y por otro, la facilidad de modificar la escala de la transformada de Fourier, puesto que tan sólo es necesario modificar la imagen de entrada, sin variar las caracter´ısticas de las lentes ni su posición. A continuación, se analizará el proceso de correlación óptica en la detección de un motivo concreto en una escena compleja que tiene lugar en un correlador de Vander Lugt, y para ello seguiremos la notación del propio Vander Lugt [Lug66, Lug92], la cual se basa en la definición de la siguiente función:

ψ(x, y; d) = e[jπ(x2+y2λD ] (5.1)

Esta funci´on representa una onda esf´erica que diverge y cuyo origen se encuentra a una distancia D del plano (x, y).

Sea un sistema iluminado con luz coherente monocrom´atica de longitud de onda λ que se expande desde el punto O. A una distancia d de este punto se encuentra situada una lente convergente (L1) de focal f10. La escena, representada por una funci´on

bidimensional f (x, y), se coloca a una distancia arbitraria d1 detr´as de esta lente.

Esta disposición corresponde al difractómetro convergente representado en la figura 1.1(c), y la distribución de luz en un plano situado a una distancia d2 de la imagen

(4)

Figura 5.1: Esquema de un correlador convergente de Vander Lugt. F (x0, y0) ∝ +∞_{Z Z} −∞ +∞_{Z Z} −∞ ψ(α, β; d)ψ∗(α, β; f₁0)ψ(α, β; d1)ψ(α, β; f10)e[−j 2παx+βy λd1 ]_×

f (x, y)ψ(x, y; d₂)ψ(x0, y0; d₂)e[−j2πxx0+yy0λd2 ]_{dα dβ dxdy} _(5.2)

La condici´on que se ha de verificar para que esta amplitud corresponda a la transfor-mada de Fourier de la escena multiplicada por una fase cuadr´atica es:

1 f0 1 = −1 d+ 1 d1+ d2 (5.3)

es decir, que la imagen del punto O a trav´es de la lente L1se forme en el plano situado

a distancia d₂ de la escena. Denominaremos a este punto imagen O0_{, mientras que}

este plano recibe el nombre de plano de Fourier, puesto que en él encontramos la transformada de Fourier de la escena junto con el término de fase cuadrático:

F (x0, y0) ≈ ψ(x0, y0; d2)F (u, v) donde u = x 0

λd2 y v =

y0

λd2 (5.4)

Es en este plano de Fourier donde se coloca el filtro, representado por la funci´on

H(u, v), y por tanto es en este plano donde se realiza el producto de las dos funciones F (u, v)H(u, v). Generalmente, el filtro es una funci´on compleja generada a partir de

la imagen que se desea detectar, representada por la funci´on g(x, y).

Utilizaremos ahora una segunda lente convergente L2 para realizar la segunda

(5)

el representado en la figura 1.1(b), donde el objeto se encuentra delante de la lente, a una distancia d3. Por lo tanto, la distribuci´on de luz en un plano P0 situado a una

distancia d0 _{de la lente vendr´a dada por la expresi´on [Lab00]:}

c(x00, y00) ∝ +∞_{Z Z} −∞ +∞_{Z Z} −∞ F (x0, y0)G∗(u, v)ψ(x0, y0, d3)ψ(α0, β0, d3)e[−j 2πα0x0+β0y0 λd3 ]_× ψ∗(α0, β0; f₂0)ψ(α0, β0; d0)ψ(x00, y00; d0)e[−j2πx00α0+y00β0λd0 ]dα0dβ0dx0dy(5.5)0

En este caso, la condici´on necesaria para que esta relaci´on se reduzca a una transfor-mada de Fourier es:

1 f0 2 = − 1 d2+ d3 + 1 d0 (5.6)

es decir, que la imagen del plano P a trav´es de la lente L2 se encuentre situada en

el plano P0_{, o plano de correlaci´}_{on, puesto que en ´el se forma la correlaci´on entre}

escena y referencia:

c(x00, y00) ∝ ψ(x00, y00; d_k)

+∞_{Z Z}

−∞

F (u, v)G∗(u, v)e[−j2π(x0x00+y0y00)d0(d2+d3)λd3 ]_dx0_dy0₌

ψ(x00, y00; dk)f µ d2+ d3 d0 x, d2+ d3 d0 y ¶ ⊗ g µ d2+ d3 d0 x, d2+ d3 d0 y ¶ (5.7) donde d_k = d0₋ d02 d2

3(d2+ d3). Analizando esta expresi´on se puede observar c´omo en

el plano de correlaci´on aparece la correlaci´on entre la escena y el motivo a detectar escalados y multiplicados por un factor de fase.

5.1.1. Filtros cl´asicos de correlaci´on

Una de las caracter´ısticas principales de los correladores tipo Vander Lugt es la uti-lización de filtros, o imágenes generadas a partir del objeto u objetos a reconocer, y que se sitúan en el plano de Fourier. Tanto el tipo de filtro como su generación son elementos determinantes en el resultado final del proceso de reconocimiento óptico.

El primer filtro utilizado en un montaje de correlación óptica fue el denominado filtro adaptado clásico ó MF1 _{[Lug64]. A partir de una imagen, representada por una}

funci´on bidimensional g(x, y), se define el MF como:

HM F(u, v) = G∗(u, v) = |G(u, v)|e−jφ(u,v) (5.8)

(6)

donde |G(u, v)| es la amplitud de la transformada de Fourier de la imagen y φ(u, v) su fase. Este filtro puede ser generado digitalmente y codificado ópticamente, aunque en un primer momento se propon´ıa el proceso para obtenerlo ópticamente: en un difractómetro se realiza la transformada de Fourier óptica de la imagen g(x, y), es decir, G(u, v), y en una pel´ıcula holográfica se registran las interferencias con una onda plana inclinada, tal y como se puede observar en la figura 1.4.

Aunque el MF se comporta de forma óptima en cuanto a relación señal - ruido2_{, no}

sucede lo mismo cuando se le aplican otros criterios. Esto ha provocado que desde su aparici´on se hayan propuesto diferentes tipos de filtros encaminados todos ellos a optimizar los resultados finales del proceso de correlaci´on.

Una de las modificaciones del MF es el denominado filtro s´olo de fase (POF)3_,

introducido en 1984 por Horner y Gianino [HG84], y definido como:

HP OF(u, v) = G ∗_{(u, v)} |G(u, v)| = e

−jφ(u,v) _(5.9)

Su principal diferencia con respecto al MF es que en este caso el filtro se genera incor-porando únicamente información de la fase de la transformada de Fourier de la imagen a detectar, cuya importancia hab´ıa quedado evidenciada anteriormente [OL81], man-teniendo la amplitud constante e igual a la unidad. Este filtro de correlación presenta la ventaja de ser más discriminante que el filtro anterior, las correlaciones presentan una menor base, y el valor del máximo es mayor. Esto hace que su caracter´ıstica más destacable sea la optimización de la eficiencia4_{, la cual permite tener una idea de la}

luz que absorbe el filtro en el proceso de detección. Que el filtro de fase sea óptimo en cuanto a eficiencia equivale a decir que toda la luz incidente se transmite al plano de correlación, y as´ı este filtro presenta unos valores superiores entre 50 y 500 veces a los del MF [HG84, FH89]. Por contra, el filtro de fase es más sensible a distorsiones y a ruido que el MF, puesto que éste último contiene toda la información de la amplitud.

Al POF se le unir´ıa m´as tarde el filtro inverso (IF)5 _{[AKJ90, KH90], definido de}

forma similar, aunque en este caso la transformada de Fourier de la imagen a detectar

2_{La relaci´on se˜}_{nal - ruido, o SNR, signal-to-noise ratio, es uno de los par´ametros de calidad}

habituales en procesado de señal, y se define como el cociente entre el valor medio del pico de correlación y su varianza. Valores más altos de SNR equivalen a detecciones de mayor calidad

3_{Phase Only Filter}

4_{La eficiencia ´optica de un filtro, o eficiencia de Horner, eval´}_{ua la fracci´on de la energ´ıa total}

presente en el plano de entrada que es recogida en el plano de correlaci´on [Cau82]

(7)

se divide por su amplitud al cuadrado:

H_IF(u, v) = G∗(u, v)

|G(u, v)|2 =

e−jφ(u,v)

|G(u, v)| (5.10)

El problema principal que presenta este filtro es la aparición de singularidades en los puntos en que la amplitud de la transformada se anula, aunque se han propuesto diversos métodos para solventar esta dificultad [AKJ90, KH90, MWW88]. De los tres filtros, éste es el que presenta mayor capacidad de discriminación y su comportamien-to es óptimo respeccomportamien-to a PCE, o peak-comportamien-to-correlation energy, un parámetro utilizado para medir la definición del pico de correlación, y para el cual el filtro inverso presenta un valor teórico igual a la unidad [KH90], lo que equivale a decir que toda la energ´ıa que atraviesa el filtro se concentra en el pico de correlación. En cuanto a aspectos a mejorar, éste es un filtro muy sensible a la presencia de ruido en la escena y presenta una eficiencia óptica inferior a la de los dos filtros anteriores.

Los tres filtros descritos se comportan de forma óptima únicamente con respecto a uno de los criterios de calidad anteriormente mencionados: as´ı, el MF es óptimo respecto a SNR, mientras que el POF lo es en cuanto a eficiencia, y el IF, respecto a PCE. Sin embargo, los resultados de cada uno de ellos en los dos otros parámetros presentan valores bastante pobres. Esto sugiere la posibilidad de diseñar filtros que tal vez no se comporten de forma óptima respecto a ninguno de los tres parámetros, pero cuyos resultados en el conjunto de los tres sean aceptables. Son los denominados filtros óptimos (OT)6 _{[Réf91], definidos de tal manera que se garantiza que siempre}

es posible encontrar un OT que se comporte mejor simult´aneamente para los tres criterios anteriores que cualquier filtro dado. Estos filtros podr´ıan considerarse una generalizaci´on de los tres anteriores, los cuales pasar´ıan a ser simplemente casos particulares de un filtro OT.

5.2. Descripci´

on del correlador. Dise˜

no b´

asico

De cara a analizar el comportamiento del correlador en función del grado de aberra-ción se trabajó con un correlador como el que se muestra en la figura 5.2.

Ambos sistemas ópticos eran lentes biconvexas, cuyas caracter´ısticas más relevantes vienen descritas en la tabla 5.1, y se encontraban iluminados por un láser con λ = 658 nm.

(8)

Figura 5.2: Configuración básica del correlador de Vander Lugt analizado. Configu-ración 1.

Sistema Radios de curvatura (mm) Espesor (mm) Material Distancia focal (mm) Lente 1 ±35.489 4.7 vidrio BK7 35.298 Lente 2 ±113.310 4.7 vidrio BK7 110.948

Tabla 5.1: Caracter´ısticas b´asicas de los sistemas ´opticos utilizados en el correlador de Vander Lugt.

De forma equivalente a como suced´ıa en el JTC, también el diseño de este correlador ven´ıa determinado en algunos aspectos por las caracter´ısticas de los elementos optoe-lectrónicos utilizados. As´ı, tanto la imagen a transformar como el filtro se introduc´ıan en el montaje utilizando unos moduladores BNS de 128×128 p´ıxeles con un interpi-xelado de 40 µm, y unas dimensiones de 5.12×5.12 mm. Teniendo en cuenta estas magnitudes, y utilizando la expresión 4.7, la distancia entre ambos moduladores para que la escala de la transformada del objeto y la del filtro coincidiesen deb´ıa estar fijada en el valor de D = P P_λ0 = 40µm·128·40µm_658nm ≈ 311.2 mm.

Las dimensiones de los moduladores determinaban nuevamente las condiciones de iluminación del correlador, ya que en el primer difractómetro la pupila de salida del sistema (primer modulador) deb´ıa estar completamente iluminada, mientras que en el segundo era la pupila de entrada (segundo modulador) la que delimitaba el diámetro m´ınimo del haz. Esto equival´ıa a fijar un diámetro para la PS del primer difractóme-tro de 7.24 mm, mientras que este mismo valor era el correspondiente al diámedifractóme-tro de la pupila de entrada del segundo sistema.

En este caso, como objeto a detectar se utilizó la imagen de un pez con 256 niveles de gris, y la escena se generó situándolo en tres posiciones diferentes en el plano corres-pondiente al modulador de entrada: una centrada en la imagen y dos desplazadas respecto a ella, tal y como se muestra en la figura 5.3. De este modo se consegu´ıa que

(9)

la imagen a detectar se viera afectada por grados diferentes de aberraci´on y se pod´ıa analizar la p´erdida (o no) de invarianza espacial en el correlador.

Figura 5.3: Objeto a detectar y escenas. Correlador de Vander Lugt.

As´ı pues, ya tenemos fijados los parámetros principales del correlador. Ahora bien, a la hora de analizar el comportamiento individual de cada sistema óptico debe te-nerse en cuenta que la configuración mostrada en la figura 5.2 no necesariamente ha de proporcionar unos valores similares de aberración para el primer y el segun-do difractómetro. Este aspecto no tendr´ıa mayor importancia si la influencia de la aberración de cada etapa del correlador en el resultado final fuese equivalente, pero tal y como ya se ha se ha analizado previamente en el JTC (apartados 4.3 - 4.5), esta influencia presenta caracter´ısticas muy dispares. En el caso del JTC monoban-co, tanto el primer como el segundo sistema óptico presentaban el mismo grado de aberración, puesto que la configuración del dispositivo no variaba entre las dos etapas.

Por lo tanto, en el análisis del correlador de Vander Lugt se debe tener en cuenta, a priori, el grado de aberración de cada difractómetro. En la configuración anterior, el valor máximo de la aberración en la pupila de salida del primer difractómetro equival´ıa aproximadamente a 3.7λ, mientras que para el segundo era inferior a 1λ.

(10)

De cara a realizar un estudio más pormenorizado se decidió incluir el análisis de dos nuevas configuraciones: una en la que los valores de aberración de ambos difractóme-tros fuesen similares, y una tercera en la que la aberración del segundo difractómetro fuese superior a la del primero.

Manteniendo los valores para la constante de difraccción y la iluminación de los mo-duladores, las nuevas distancias de trabajo son las que se muestran en las figuras 5.4 y 5.5. En ambos casos se mantiene constante la configuración del primer difractómetro, y, por lo tanto, su aberración, mientras que se modifica la correspondiente al segundo difractómetro: en la configuración 2 su aberración corresponde a aproximadamente 3.5λ, semejante a la del primer difractómetro, mientras que en la configuración 3 aumenta hasta un valor de 9λ, sensiblemente superior a la del primer difractómetro.

Figura 5.4: Configuraci´on 2 del correlador de Vander Lugt. Aberraciones similares en ambos difract´ometros.

Figura 5.5: Configuración 3 del correlador de Vander Lugt. Aberración superior en el segundo difractómetro.

5.3. An´

alisis de la influencia de los difract´

ometros

5.3.1. Influencia del primer difract´ometro

El procedimiento que se siguió para evaluar la influencia de la calidad del sistema óptico sobre la primera transformada de Fourier y, por lo tanto, en el proceso global de correlación, se basó en el cálculo de correlaciones digitales mediante dos

(11)

trans-formadas de Fourier en cascada. La primera de ellas, correspondiente a la escena, era obtenida mediante la simulación detallada del sistema óptico real, tal y como se ha descrito anteriormente en la sección 3.1. La segunda transformada se calculaba utilizando un algoritmo digital de transformada de Fourier, es decir, asumiendo que el segundo difractómetro se encontraba libre de aberraciones.

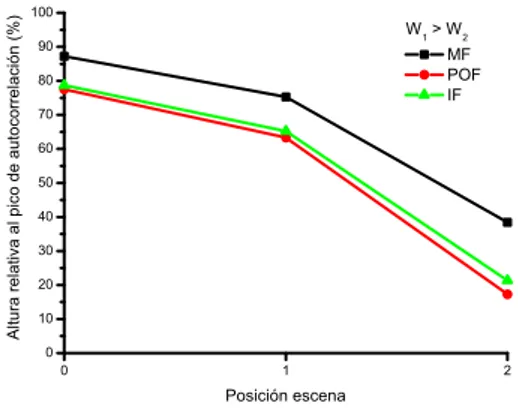
El objetivo era analizar los cambios producidos en los picos de correlación obtenidos en el caso ideal con los calculados mediante este procedimiento, y as´ı la figura 5.6 muestra los valores de los picos de correlación referidos al pico de autocorrelación pa-ra la imagen libre de aberpa-ración. Estos valores corresponden a la configupa-ración 1 del correlador. Puesto que en este caso únicamente se considera la aberración del primer difractómetro, y la segunda transformada se realiza de forma exacta, los resultados correspondientes a las dos configuraciones restantes son idénticos a los presentados en la figura 5.6, ya que en ellas únicamente se modificaba la configuración del segundo difractómetro. 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A l t u r a r e l a t i va a l p i co d e a u t o co r r e l a ci ó n ( % ) Posición escena W 1 > W 2 MF POF IF

Figura 5.6: Alturas relativas a la correlación ideal de los picos de correlación simulados considerando únicamente la aberración del primer difractómetro. Configuración 1.

El comportamiento de los tres filtros es notablemente similar, y cabe destacar el des-censo de la altura relativa de los picos de correlación a medida que la posición del objeto se desplaza hacia puntos más alejados del centro de la imagen, y afectados, por tanto, por valores más altos de aberración. Por lo tanto, los correladores reales, es decir, aquellos en los que se consideran las aberraciones de los sistemas ópticos que los forman, no son espacialmente invariantes. Esto puede ser un problema a tener en cuenta en situaciones, por ejemplo, de seguimiento de objetos a lo largo de una

(12)

escena compleja, o bien en el caso de trabajar con escenas multiobjeto, con imágenes a detectar situadas en diferentes posiciones de la escena a analizar. En ambos casos, la elección de un valor umbral a partir del cual discriminar los picos de detección respecto de aquellos picos erróneos puede resultar sumamente compleja, y variar en función del sistema óptico utilizado.

5.3.2. Influencia del segundo difract´ometro

El análisis del segundo difractómetro es sensiblemente más complicado, puesto que su sistema óptico recibe frentes de onda provenientes de los múltiples órdenes de difracción situados fuera de eje, los cuales son generados por el modulador donde se muestra el filtro de correlación. Ahora bien, tal y como se comentó anteriormente en el apartado 2.3, podemos utilizar la óptica geométrica para describir la propagación de la luz entre la pupila de entrada y la de salida del sistema, mientras que los efectos difractivos únicamente se consideran durante la propagación desde la pupila de salida hasta el plano imagen.

En el segundo difractómetro el modulador, donde se realiza la superposición entre la transformada de Fourier de la escena y el filtro correspondiente, actúa de pupila de entrada. Por lo tanto, el cálculo de la correlación considerando solamente los efectos de la aberración del segundo difractómetro se puede resumir según el siguiente procedimiento:

1. Cálculo de la transformada de Fourier ideal de la escena mediante un algoritmo FFT, que corresponde al resultado del primer difractómetro, considerado libre de aberración.

2. C´alculo de la imagen mostrada en el segundo modulador, entendida como el resultado del producto complejo de la transformada de Fourier de la escena por el filtro considerado.

3. Determinación de la posición de la pupila de salida del segundo difractómetro, y de sus aumentos geométricos.

4. Cálculo de la aberración del segundo sistema en el plano de la pupila de salida. 5. Multiplicación de la imagen del segundo modulador, obtenida en el paso 2, por los aumentos del segundo difractómetro, lo que equivale a trasladar esta imagen hasta la pupila de salida.

(13)

6. Propagaci´on de esta imagen hasta el plano de correlaci´on mediante transfor-mada de Fourier digital.

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu r a r e la t iva a l p ico d e a u t o co r r e la ci ó n (% ) Posición escena W1 > W2 MF POF IF (a) Configuración 1 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu r a r e la t iva a l p ico d e a u t o co r r e la ci ó n (% ) Posición escena W1 ≈ W2 MF POF IF (b) Configuración 2 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltr u a r e la t iva a l p ico d e a u t o co r r e la ci ó n (% ) Posición escena W 1 < W 2 MF POF IF (c) Configuración 3

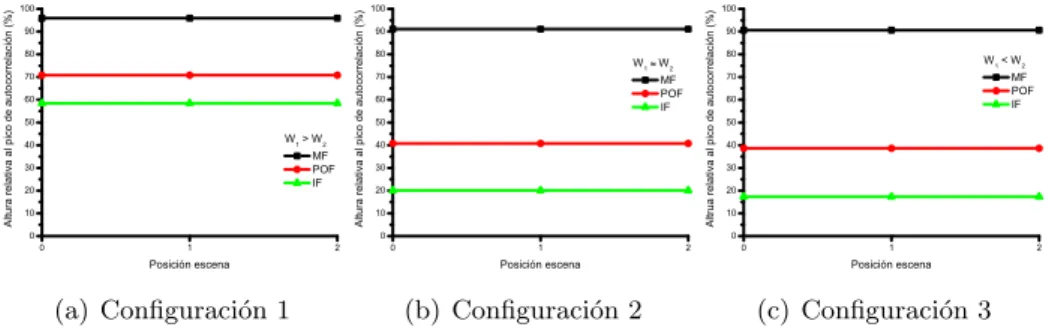
Figura 5.7: Alturas relativas a la correlación ideal de los picos de correlación simulados considerando únicamente la aberración del segundo difractómetro. Configuraciones 1, 2 y 3.

De la observación de los resultados obtenidos (figura 5.7) se puede concluir que la caracter´ıstica más importante introducida por el segundo difractómetro es un des-censo significativo de la altura de los picos de correlación, incluso en la posición 0, correspondiente a la imagen centrada del pez. Este descenso, por otra parte, afecta por igual a todos los puntos de la escena, es decir, es independiente de la posición de la escena dentro del plano objeto. Esta disminución en los valores se manifiesta especialmente al utilizar el filtro inverso, mientras que por contra, el filtro adaptado se muestra bastante resistente a este efecto. Por otro lado, tal y como era de esperar, a medida que aumenta el valor de la aberración, tanto mayor es el descenso en la altura de los picos, y as´ı, por ejemplo podemos llegar a obtener valores inferiores al 20 %, tal y como sucede con la configuración 3 al utilizar el filtro inverso.

5.3.3. An´alisis del proceso global

Finalmente, vamos a considerar el caso en que tenemos en cuenta los efectos de la aberración en la correlación final de tanto el primer como el segundo difractómetro. En este caso, se propaga la imagen aberrada presente en el primer modulador hasta el plano correspondiente a la posición del segundo modulador (imagen paraxial del punto objeto), donde se multiplica por el filtro. El resultado de este producto se tras-lada al plano donde se encuentra la pupila de salida del segundo sistema, es decir, la imagen de este modulador, puesto que éste actúa de pupila de entrada. Es en este plano donde se le añade la aberración correspondiente, para finalmente propagar el

(14)

resultado hasta el plano de correlación. 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu ra r e la t iva a l p i co d e a u to co r r e la ci ó n ( % ) Posición escena W 1 > W 2 MF POF IF (a) Configuración 1 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu r a r e la t iva a l p ico d e a u to co r r e la ci ó n (% ) Posición escena W 1≈ W 2 MF POF IF (b) Configuración 2 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu ra r e la t iva a l p i co d e a u to co r r e la ci ó n ( % ) Posición escena W1 < W2 MF POF IF (c) Configuración 3

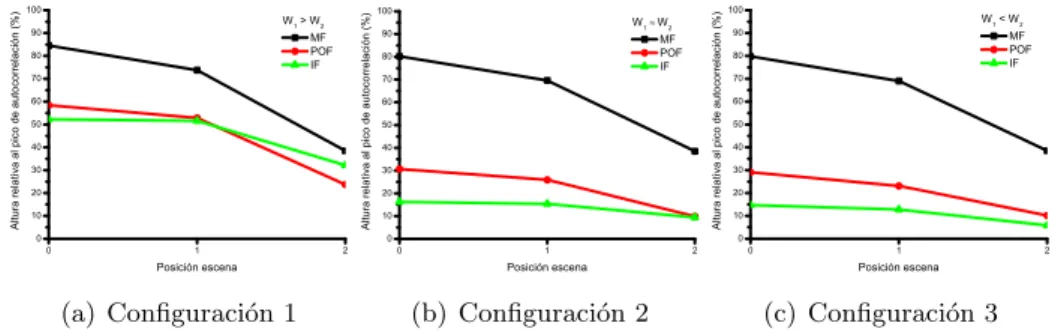
Figura 5.8: Alturas relativas a la correlación ideal de los picos de correlación simulados considerando la aberración de ambos difractómetros. Configuraciones 1, 2 y 3.

En este caso tambi´en se analizaron las tres configuraciones del correlador, y, tal y como se puede apreciar en la figura 5.8, los resultados coinciden con lo previsto inicialmente:

1. la influencia de la aberración del primer difractómetro genera varianza espacial, de manera que posiciones más alejadas del eje óptico, y por lo tanto, con valores más altos de aberración, equivalen a altura de picos de correlación menores. 2. la aberración del segundo difractómetro provoca un descenso generalizado en

la altura de los picos de correlación, tanto más acusado cuanto mayor es la aberración del sistema.

3. el filtro adaptado mantiene una cierta robustez a la influencia de la aberraci´on, con valores superiores al 40 % incluso en las situaciones m´as desfavorables. 4. tanto el filtro inverso como el de fase resultan especialmente sensibles a los

efectos de la aberraci´on, llegando a valores inferiores al 10 %.

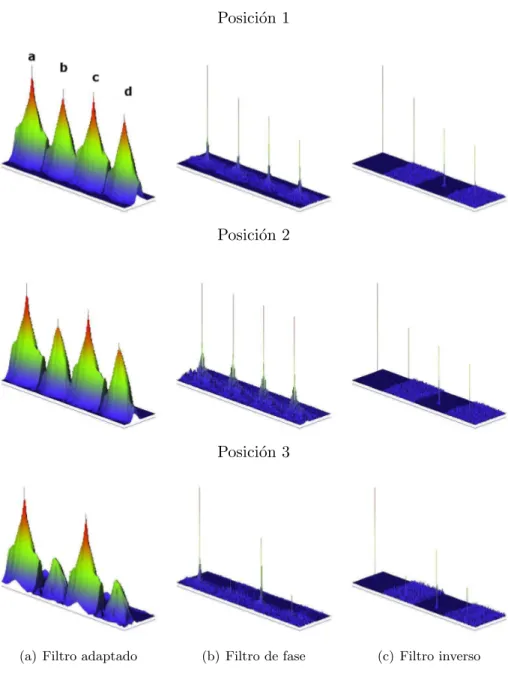
Las figuras 5.9 - 5.11 muestran representaciones tridimensionales de la intensidad de correlación entre las imágenes de la figura 5.3 y los tres filtros generados a partir del objeto libre de aberración, para cada una de las configuraciones del correlador analizadas. En cada una de estas figuras, las filas se corresponden a las tres posiciones posibles de la escena, mientras que las columnas indican el tipo de filtro utilizado: adaptado, de fase e inverso. Por otro lado, los cuatro picos en cada una de las imágenes se corresponden a las diferentes posibilidades que se consideraron al tener en cuenta la aberración de cada difractómetro:

(15)

Considerar ambos difract´ometros libres de aberraci´on.

Considerar únicamente la aberración del primer difractómetro. Considerar únicamente la aberración del segundo difractómetro. Considerar la aberración en ambos difractómetros.

5.4. Influencia de la posici´

on de los moduladores

respec-to de los sistemas ´

opticos

En el apartado 4.3.4 se propuso un método para mejorar los valores de los picos de correlación obtenidos en el JTC. A partir del análisis de la evolución de los picos al desplazar el plano de captación, y de la influencia de la aberración del primer y del segundo difractómetro, se realizaba la captación del JPS en el plano en que la esta-bilidad de los picos era más elevada, mientras que la captación de la correlación final se realizaba en el plano en que el descenso de los valores de los picos de correlación debido a la influencia del segundo difractómetro era menor. Ahora bien, esta confi-guración corresponder´ıa a un dispositivo experimental que operara con dos montajes difractivos independientes, o bien con un solo difractómetro al cual se le modificara la posición del plano de captación entre ambas transformadas.

En el caso que nos ocupa, ambos sistemas ópticos no actúan de forma independiente, sino que se encuentran ligados por la distancia entre los dos moduladores, la cual permite que la escala de la transformada de Fourier de la escena se ajuste a la del filtro. Esto hace que modificar esta distancia, reduciéndola, por ejemplo, lo que equi-valdr´ıa a colocar el filtro en un plano diferente del paraxial, y más cercano al primer sistema óptico, resulte inviable sin modificar otros parámetros del sistema, como por ejemplo, el interpixelado de los moduladores, la longitud de onda de la luz utilizada o la distancia focal de los sistemas ópticos.

Si nos ceñimos a una situación cercana a la realidad, resulta más adecuado despla-zar el conjunto formado por ambos moduladores, manteniendo fija la distancia entre ellos. Esto se traduce en varios efectos: por un lado, desplazar el primer modulador equivale a modificar la posición de la pupila de salida del primer sistema, y, por lo tanto, la aberración de este difractómetro. Por otra parte, estamos desplazando tam-bién el punto objeto del segundo difractómetro, as´ı como la posición de su pupila de

(16)

Posici´on 1

Posici´on 2

Posici´on 3

(a) Filtro adaptado (b) Filtro de fase (c) Filtro inverso

Figura 5.9: Representaciones tridimensionales de la intensidad de la correlación simu-lada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro, c) corre-lación considerando únicamente la aberración del segundo difractómetro, d) correla-ción considerando la aberracorrela-ción del primer y del segundo difractómetros. Configura-ción 1.

(17)

Posici´on 1

Posici´on 2

Posici´on 3

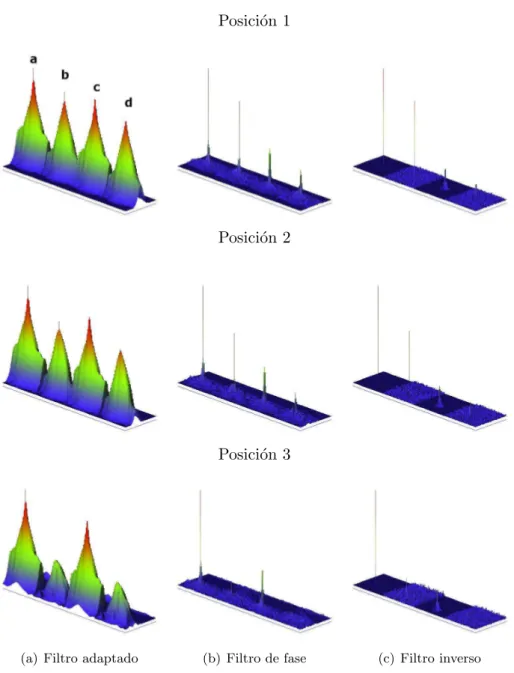
Figura 5.10: Representaciones tridimensionales de la intensidad de la correlación simulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractóme-tro, c) correlación considerando únicamente la aberración del segundo difractómetro, d) correlación considerando la aberración del primer y del segundo difractómetros. Configuración 2.

(18)

Posici´on 1

Posici´on 2

Posici´on 3

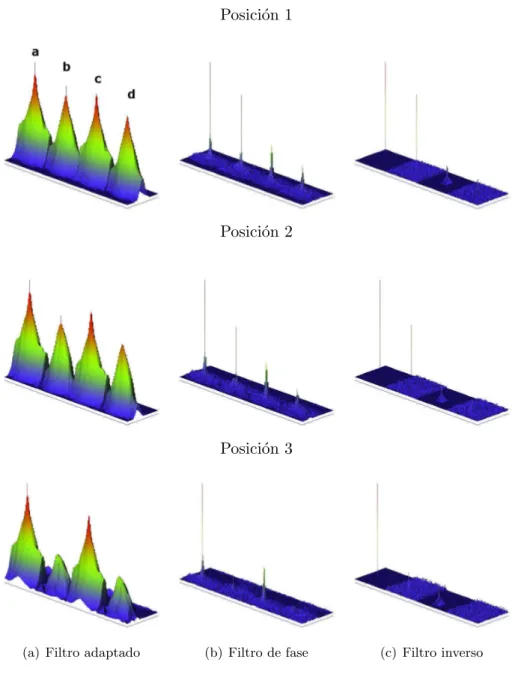
Figura 5.11: Representaciones tridimensionales de la intensidad de la correlación simulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractóme-tro, c) correlación considerando únicamente la aberración del segundo difractómetro, d) correlación considerando la aberración del primer y del segundo difractómetros. Configuración 3.

(19)

entrada. Esto modificará la posición de la pupila de salida, el cálculo de los aumentos del sistema y, finalmente, influirá en el valor de la aberración del segundo difractóme-tro.

Se procedió a realizar un estudio detallado de la evolución de los picos de correlación para diferentes desplazamientos de ambos correladores respecto a la configuración inicial (figura 5.2). Se decidió analizar un conjunto de 12 posiciones diferentes (in-cluida la posición del plano paraxial), considerando la aberración debida a ambos difractómetros. Debe tenerse en cuenta, por otra parte, que desplazar los modulado-res también implica modificar los valomodulado-res de abertura de ambos sistemas, de manera que se mantenga fijo el diámetro de la pupila de salida (en el primer difractómetro) y el de la pupila de entrada (en el segundo difractómetro), pues ambos quedan deter-minados por las dimensiones de los moduladores. Los resultados obtenidos para cada uno de los filtros utilizados son los que se muestran en la figura 5.12.

Si analizamos con detalle estos resultados vemos como a medida que desplazamos ambos moduladores hacia el primer sistema óptico (desplazamientos negativos), tan-to para el filtro adaptado como para el de fase, y para las tres posiciones de la escena, aumentan los valores de los picos de correlación. En el caso del filtro inverso esta ten-dencia se mantiene para la posición más alejada del eje óptico (posición 2), mientras que los valores para las otras dos posiciones disminuyen ligeramente. As´ı pues, se puede concluir que reducir la distancia entre el primer sistema óptico y el conjunto de ambos moduladores, manteniendo fija la separación entre ambos, mejora los re-sultados de la detección.

Ahora bien, ya hemos comentado anteriormente que este desplazamiento implica tam-bién una variación en los valores de la aberración tanto del primer como del segundo difractómetro. Por lo tanto, tal vez esta mejora en la correlación final sea debida a una disminución en la aberración de los sistemas y no sólo a que las transformadas sean mejores en otro plano. Para descartar o confirmar este aspecto, se calculó el valor de la aberración en cada uno de los planos analizados para ambos sistemas:

Para el primer difractómetro, los valores de aberración oscilaban entre las 4.17λ para el plano situado en la posición +15 y las 2.83λ correspondiente al plano situado en la posición -20, con una disminución gradual para los planos que se encuentran entre ambos. Por lo tanto, la aberración del primer sistema dismi-nuye a medida disminuimos su distancia a ambos moduladores.

(20)

-25 -20 -15 -10 -5 0 5 10 15 20 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e l a t i va a l p i co d e a u t o co r r e l a ci ó n ( % )

Desplazamiento de los moduladores (mm) MF (Ab. global)

Posición 0 Posición 1 Posición 2

(a) Filtro adaptado

-25 -20 -15 -10 -5 0 5 10 15 20 0 10 20 30 40 50 60 70 80 90 100 A l t u r a r e l a t i va a l p i co d e a u t o co r r e l a ci ó n ( % )

Desplazamiento de los moduladores (mm) POF (Ab. global)

Posición 0 Posición 1 Posición 2 (b) Filtro de fase -25 -20 -15 -10 -5 0 5 10 15 20 0 10 20 30 40 50 60 70 80 90 100 A l t u r a r e l a t i va a l p i co d e a u t o co r r e l a ci ó n ( % )

Desplazamiento de los moduladores (mm) IF (Ab. global)

Posición 0 Posición 1 Posición 2

(c) Filtro inverso

Figura 5.12: Evolución de la altura relativa a la correlación ideal de los picos de correlación simulados en función de la posición relativa de los moduladores respecto de los sistemas ópticos considerando la aberración de ambos difractómetros.

(21)

En el caso del segundo difractómetro, estos valores eran de 0.74λ para el plano de posición +15 y de 0.96λ para el plano situado en la posición -20, variando de manera progresiva entre uno y otro. Esto quiere decir que la aberración del segundo difractómetro disminuye cuando la distancia entre los moduladores y el segundo sistema óptico se reduce.

5.5. Generaci´

on de filtros adaptados a sistemas ´

opticos

aberrados

Una de las posibilidades que ofrece el correlador de Vander Lugt es la amplia gama de filtros que se pueden generar. En nuestro caso hemos estado trabajando con filtros generados a partir de la imagen a detectar (mostrada en la figura 5.3). Ahora bien, en el caso real de un correlador, la imagen que se superpone con el filtro no es la imagen ideal, libre de aberración, tal y como se muestra en la figura anterior, sino que esta imagen se verá modificada por las aberraciones introducidas por los sistemas ópticos presentes en el correlador. Parece por tanto adecuado realizar un diseño de filtros más espec´ıfico para el correlador con el que estemos trabajando, teniendo en cuenta este aspecto. Esto equivale a diseñar los filtros no a partir de la imagen ideal a detectar, sino a partir de esta imagen una vez ha sido modificada por las aberraciones.

Sin embargo hay que tener en cuenta que esta posibilidad, es decir, el poder compensar la aberración del sistema óptico a partir de un diseño inteligente de los filtros, impli-ca un proceso diferente en función del difractómetro que estemos considerando. As´ı, mientras se trabaja considerando únicamente la aberración del primer difractómetro, el filtro debe diseñarse a partir de la imagen afectada por esta aberración, de manera que permita detectar exactamente la imagen de la cual vamos a realizar su transfor-mada. Por el contrario, al considerar la aberración del segundo difractómetro, puesto que esta aberración influye de forma posterior a la introducción del filtro, éste debe generarse incorporando la fase conjugada de la aberración del difractómetro, de modo que en el proceso global quede de esta manera compensada.

As´ı pues, podr´ıamos llegar a generar cuatro conjuntos de filtros, en funci´on de los aspectos a analizar:

1. Filtros generados a partir de la imagen sin aberrar.

(22)

del primer difract´ometro.

3. Filtros generados a partir de la imagen afectada únicamente por la aberración ”conjugada” del segundo difractómetro.

4. Filtros generados a partir de la imagen afectada por la aberraci´on de ambos difract´ometros.

Teniendo todos estos aspectos en cuenta, los resultados que se obtuvieron en las si-mulaciones realizadas para la configuración con aberraciones similares para ambos difractómetros (configuración 2) son los que se muestran en la figura 5.13. En esta figura, las columnas se corresponden a cada uno de los filtros generados (MF, POF o IF), mientras que las filas se refieren al grado de aberración considerado: únicamente en el primer difractómetro, únicamente en el segundo difractómetro, o en ambos. Para su comparación se muestran igualmente los resultados correspondientes al caso en que el filtro se encontraba generado a partir de la imagen sin aberrar, y que ya se hab´ıan mostrado previamente en las figuras 5.6, 5.7 y 5.8.

De la observación de estos resultados podemos deducir una serie de consideraciones: el aspecto más destacado es la mejora sustancial en todos los casos de los valores correspondientes a la altura de los picos de correlación, en comparación con los valo-res corvalo-respondientes al supuesto en que los filtros utilizados hubiesen sido generados a partir de la imagen ideal, libre de aberraciones. Tal y como ser´ıa de esperar, esta mejora alcanza su nivel más alto cuando analizamos los datos correspondientes a la detección de la imagen a partir de la que se ha generado el filtro. As´ı, por ejemplo, para la posición 0, la correspondiente al pez centrado en la imagen, en todos los casos se consigue un valor del 100 % en la altura del pico, mejorando de forma evidente los resultados previos, especialmente los referidos a los filtros de fase e inverso en el caso de considerar la aberración en el proceso global.

Resulta destacable cómo se recupera este valor del 100 % independientemente de la posición de la escena al considerar únicamente la aberración del segundo difractóme-tro. Ya se comentó anteriormente que en este supuesto se produc´ıa una variación en la altura de los picos, pero que se manten´ıa la invarianza espacial. Por lo tanto, si ahora ya no se produce este descenso en la altura de los picos, y al mismo tiempo se mantiene un valor constante para todos ellos, el resultado es un valor global del 100 %.

(23)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e sp e ct o a l p ico d e a u t o co r r e la ci ó n ( % ) Posición de la escena MF (considerando aber. sólo en 1r difract.)

Filtro generado con imagen sin aberrar Filtro generado con imagen + aber. 1r difract.

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu r a r e sp e ct o p ico d e a u to co r r e la ci ó n ( % ) Posición de la escena POF (considerando aber. sólo en 1r difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu r a r e sp e ct o p ico d e a u to co r r e la ci ó n ( % ) Posición de la escena IF (considerando aber. sólo en 1r difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A l tu r a re sp e ct o p i co d e a u to co r r re la ci ó n ( % ) Posición de la escena MF (considerando aber. sólo en 2n difract.)

Filtro generado con imagen sin aberrar Filtro generado con imagen + aber. 2n difract.

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e sp e ct o p ico d e a u t o co r re la ci ó n ( % ) Posición de la escena POF (considerando aber. sólo en 2n difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e sp e ct o p ico d e a u t o co r re la ci ó n ( % ) Posición de la escena IF (considerando aber. sólo en 2n difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A l tu r a re sp e ct o p ico d e a u to co r r e la ci ó n (% ) Posición de la escena MF (considerando aber. global)

Filtro generado con imagen sin aberrar Filtro generado con imagen + aber. global

(a) Filtro adaptado

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A l tu r a re sp e ct o p ico d e a u to co r r e la ci ó n (% ) Posición de la escena POF (considerando aber. global)

(b) Filtro de fase 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e l a tiva a l p ico d e a u to co r r e la ci ó n ( % ) Posición de la escena IF (considerando aber. global)

(c) Filtro inverso

Figura 5.13: Alturas relativas a la correlación ideal de los picos de correlación simu-lados para las tres posiciones de la escena y tres supuestos: correlación considerando ´

unicamente la aberración del primer difractómetro, únicamente la del segundo di-fractómetro, o la de ambos, mediante la utilización de filtros generados incluyendo la aberración del primer difractómetro, del segundo o la del proceso global. Configura-ción 2.

(24)

Finalmente, de manera similar al apartado 5.3.3, las figuras 5.14 - 5.17 muestran representaciones tridimensionales de la intensidad de correlación. Cada una de es-tas figuras se corresponde con uno de los cuatro conjuntos de filtros especificados anteriormente, y en todas ellas las filas se corresponden a cada una de las tres po-siciones posibles de la escena, mientras que las columnas indican el tipo de filtro utilizado: adaptado, de fase e inverso. Igualmente, los cuatro picos se refieren a las diferentes posibilidades que se consideraron al tener en cuenta la aberración de cada difractómetro:

Considerar ambos difract´ometros libres de aberraci´on. Caso ideal7_.

Considerar únicamente la aberración del primer difractómetro.

Considerar únicamente la aberración del segundo difractómetro.

Considerar la aberraci´on en ambos difract´ometros.

5.6. Dise˜

no de un correlador de Vander Lugt ´

optimo

En los apartados anteriores se han analizado diferentes aspectos de la influencia de las aberraciones de los sistemas ópticos en el proceso final de correlación en un correlador de Vander Lugt. También se han propuesto una serie de métodos para aumentar la altura de los picos de correlación y mejorar la invarianza espacial del dispositivo. El propósito de este apartado es el de recoger todo este conjunto de resultados en un ´

unico dise˜no utilizando como base la configuraci´on mostrada en la figura 5.2.

Para diseñar este correlador se tendrán en cuenta dos aspectos principales: por un lado, la evolución de la altura de los picos de correlación en función de la posición de los moduladores con respecto a los sistemas ópticos, analizada en el apartado 5.4, y por otro lado los resultados obtenidos utilizando los filtros adaptados a la aberración de los difractómetros.

Del análisis de los resultados mostrados en la figura 5.12, y a partir del cálculo de los valores de aberración en posiciones extremas de los moduladores, se observó que a medida que la separación entre el primer sistema óptico y el primer modulador disminu´ıa, el valor de la aberración introducida por el primer difractómetro también

(25)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.14: Representaciones tridimensionales de la intensidad de la correlación simulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractóme-tro, c) correlación considerando únicamente la aberración del segundo difractómetro, d) correlación considerando la aberración del primer y del segundo difractómetros. Filtros generados a partir de la imagen sin aberración. Configuración 2.

(26)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.15: Representaciones tridimensionales de la intensidad de la correlación si-mulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro, c) correlación considerando únicamente la aberración del segundo difractómetro (sin trascendencia real, en este caso), d) correlación considerando la aberración del pri-mer y del segundo difractómetros. Filtros generados a partir de la imagen afectada por la aberración del primer difractómetro. Configuración 2.

(27)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.16: Representaciones tridimensionales de la intensidad de la correlación si-mulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro (sin trascendencia real, en este caso), c) correlación considerando únicamente la aberra-ción del segundo difractómetro, d) correlaaberra-ción considerando la aberraaberra-ción del primer y del segundo difractómetros. Filtros generados a partir de la imagen afectada por la aberración del segundo difractómetro. Configuración 2.

(28)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.17: Representaciones tridimensionales de la intensidad de la correlación si-mulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro, c) corre-lación considerando únicamente la aberración del segundo difractómetro d) correla-ción considerando la aberracorrela-ción del primer y del segundo difractómetros. Filtros generados a partir de la imagen afectada por la aberración de ambos difractómetros. Configuración 2.

(29)

era menor. De forma paralela, aproximar el segundo modulador al segundo sistema óptico también provocaba una disminución de la aberración del segundo difractómetro. Por lo tanto, parece lógico suponer que cuanto menor sean estas distancias (L1 -SLM1 y SLM2 - L2), tanto menor será la aberración introducida por cada una de las etapas del correlador, de manera que la configuración óptima se corresponda a elimi-nar completamente la separación entre los sistemas y los moduladores, tal y como se muestra en la figura 5.18. Esta configuración presenta para el primer difractómetro un valor máximo de la aberración de 1.95λ, mientras que para el segundo difractóme-tro la aberración correspondiente es de ´unicamente 0.06λ.

Figura 5.18: Configuraci´on ´optima del correlador de Vander Lugt.

Finalmente, tal y como se ha comentado en el apartado anterior 5.5, la utilización de filtros adaptados a la aberración de cada difractómetro, de manera que en el proceso de correlación real sean eliminados sus efectos, mejora sensiblemente los resultados obtenidos. La figura 5.19 muestra los resultados que se obtuvieron en las simulacio-nes realizadas para la configuración anterior. De forma semejante a los resultados presentados en la figura 5.13, las columnas se corresponden a cada uno de los filtros generados (MF, POF o IF), mientras que las filas se refieren a la aberración con-siderada, ya sea únicamente en el primer difractómetro, únicamente en el segundo difractómetro, o en ambos. De cara a poder evaluar la bondad de los resultados se encuentran resaltados los correspondientes a filtros generados a partir de la imagen sin aberrar y los relativos a los filtros diseñados incorporando la información sobre la aberración de ambos difractómetros.

Las figuras 5.20 - 5.23 muestran las representaciones tridimensionales de la intensidad de correlaci´on. Cada uno de estos conjuntos de im´agenes se han generado utilizando

(30)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e la tiva a l p i co d e a u to co r r e la ci ó n ( % ) Posición de la escena MF (considerando aber. sólo en 1r difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e la tiva a l p i co d e a u to co r r e la ci ó n ( % ) Posición de la escena POF (considerando aber. sólo en 1r difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u r a r e la tiva a l p i co d e a u to co r r e la ci ó n ( % ) Posición de la escena IF (considerando aber. sólo en 1r difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu ra r e la t iva a l p ico d e a u t o co r re la ci ó n ( % ) Posición de la escena MF (considerando aber. sólo en 2n difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu ra r e la t iva a l p ico d e a u t o co r re la ci ó n ( % ) Posición de la escena POF (considerando aber. sólo en 2n difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A ltu ra r e la t iva a l p ico d e a u t o co r re la ci ó n ( % ) Posición de la escena IF (considerando aber. sólo en 2n difract.)

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u ra r e la t iva a l p ico d e a u to co r r e la ci ó n (% ) Posición de la escena MF (considerando aber. global)

(a) Filtro adaptado

0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u ra r e la t iva a l p ico d e a u to co r r e la ci ó n (% ) Posición de la escena POF (considerando aber. global)

(b) Filtro de fase 0 1 2 0 10 20 30 40 50 60 70 80 90 100 A lt u ra r e la t iva a l p ico d e a u to co r r e la ci ó n (% ) Posición de la escena IF (considerando aber. global)

(c) Filtro inverso

Figura 5.19: Alturas relativas a la correlación ideal de los picos de correlación simu-lados para las tres posiciones de la escena y tres supuestos: correlación considerando ´

unicamente la aberración del primer difractómetro, únicamente la del segundo di-fractómetro, o la de ambos, mediante la utilización de filtros generados incluyendo la aberración del primer difractómetro, del segundo o la del proceso global. Configura-ción óptima del correlador.

(31)

uno de los cuatro tipos de filtros especificados anteriormente. As´ı, para obtener las correlaciones de la figura 5.20 se han utilizado los filtros MF, POF y IF generados a partir de la imagen centrada del pez sin aberración; las de la figura 5.21 se obtuvieron mediante la utilización de los filtros generados a partir de la imagen centrada del pez modificada por la aberración del primer difractómetro8_{; para obtener las}

correlacio-nes de la figura 5.22 se utilizaron filtros diseñados a partir de la imagen centrada del pez afectada por la aberración conjugada del segundo difractómetro9. Finalmen-te, el conjunto mostrado en la figura 5.23 corresponder´ıa al caso en que los filtros se diseñaron a partir de la imagen centrada del pez afectada por la aberración del primer difractómetro y la aberración conjugada del segundo. En todos los casos, de todas maneras, el valor de referencia corresponde a la correlación ideal, considerando ambos difractómetros libres de aberración, y con los filtros generados, por lo tanto, a partir de la imagen sin aberración.

Del mismo modo que suced´ıa en otros conjuntos similares ya mostrados (ver figura 5.9), las filas se corresponden a cada una de las tres posiciones posibles de la escena, mientras que las columnas indican el tipo de filtro utilizado: adaptado, de fase e inverso. Por último, los cuatro picos se refieren a las diferentes posibilidades que se consideraron al tener en cuenta la aberración de cada difractómetro:

Considerar ambos difractómetros libres de aberración. Caso ideal10. Considerar únicamente la aberración del primer difractómetro. Considerar únicamente la aberración del segundo difractómetro. Considerar la aberración de ambos difractómetros.

8_{En este caso la correlación correspondiente al supuesto en que sólo se considera la aberración}

del segundo difract´ometro tiene un sentido exclusivamente acad´emico, sin trascendencia real.

9_{En este caso la correlación correspondiente al supuesto en que sólo se considera la aberración}

del primer difract´ometro tiene un sentido exclusivamente acad´emico, sin trascendencia real.

(32)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.20: Representaciones tridimensionales de la intensidad de la correlación si-mulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro, c) corre-lación considerando únicamente la aberración del segundo difractómetro, d) corre-lación considerando la aberración del primer y del segundo difractómetros. Filtros generados a partir de la imagen sin aberración. Configuración óptima del correlador.

(33)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.21: Representaciones tridimensionales de la intensidad de la correlación si-mulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro, c) correlación considerando únicamente la aberración del segundo difractómetro (sin trascendencia real, en este caso), d) correlación considerando la aberración del pri-mer y del segundo difractómetros. Filtros generados a partir de la imagen afectada por la aberración del primer difractómetro. Configuración óptima del correlador.

(34)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.22: Representaciones tridimensionales de la intensidad de la correlación si-mulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro (sin trascendencia real, en este caso), c) correlación considerando únicamente la aberra-ción del segundo difractómetro, d) correlaaberra-ción considerando la aberraaberra-ción del primer y del segundo difractómetros. Filtros generados a partir de la imagen afectada por la aberración del segundo difractómetro. Configuración óptima del correlador.

(35)

Posici´on 1

Posici´on 2

Posici´on 3

Figura 5.23: Representaciones tridimensionales de la intensidad de la correlación si-mulada para las tres posiciones de la escena y cuatro supuestos: a) correlación ideal, b) correlación considerando únicamente la aberración del primer difractómetro, c) corre-lación considerando únicamente la aberración del segundo difractómetro, d) corre-lación considerando la aberración del primer y del segundo difractómetros. Filtros generados a partir de la imagen afectada por la aberración de ambos difractómetros. Configuración óptima del correlador.

(36)

5.7. Consideraciones generales

En los apartados anteriores se han analizado los resultados obtenidos al estudiar di-ferentes aspectos del proceso de correlación en un correlador convergente de Vander Lugt. Esta sección pretende sintetizarlos, de modo que sirva para otorgar una visión global de cómo las aberraciones de los sistemas ópticos modifican los picos de corre-lación, as´ı como de cuáles son algunas de las estrategias que se pueden utilizar para minimizar sus efectos.

En el estudio anterior se ha diseñado un correlador de Vander Lugt formado por dos lentes biconvexas, y una vez efectuado el estudio de los resultados para diferentes configuraciones del conjunto, se ha intentado reducir la influencia de las aberraciones. Para ello se han seguido dos procedimientos: por un lado, modificar la configuración original mediante el desplazamiento del conjunto de ambos moduladores respecto de los sistemas ópticos, y por otra parte, diseñando filtros que compensasen la aberración introducida por los sistemas ópticos. Finalmente, a la vista de los efectos observados se propone una configuración óptima.

Influencia de la aberración de cada difractómetro en la correlación final Se ha diseñado un correlador convergente de Vander Lugt que utiliza como sistemas ópticos dos lentes biconvexas, y una fuente de luz coherente con λ = 658 nm. Tanto la imagen a transformar como el filtro se introducen en el montaje utilizando unos moduladores BNS de 128×128 p´ıxeles con un interpixelado de 40 µm, y unas dimen-siones de 5.12×5.12 mm. Como objeto a detectar se ha utilizado la imagen de un pez con 256 niveles de gris, y las escenas se han generado situándolo en tres posiciones diferentes en el plano correspondiente al modulador de entrada: una centrada en la imagen y dos desplazadas respecto a ella. De este modo se consigue que la imagen a detectar se vea afectada por grados diferentes de aberración.

Se han calculado las aberraciones de cada uno de los difractómetros para tres configu-raciones diferentes del correlador anterior, correspondientes a otras tantas distancias entre el segundo modulador y el segundo sistema óptico. Esta variación influye en el valor de la aberración máxima introducida por el segundo difractómetro, de modo que se han analizado configuraciones donde la aberración del primer difractómetro era sensiblemente superior a la del segundo; donde ambas ten´ıan valores similares, y una tercera en que la aberración del segundo difractómetro era superior a la del

(37)

primero. De este modo se pretende que la diferencia relativa entre ambas aberraciones no altere el an´alisis de la altura de los picos de correlaci´on.

Independientemente de la configuración utilizada, se comprueba que la influencia de la aberración del primer difractómetro, de forma similar a como ocurr´ıa al estudiar el JTC, se traduce fundamentalmente en una disminución progresiva de la altura de los picos de correlación a medida que la escena se ve afectada por valores más altos de aberración, es decir, a medida que la imagen se aleja del centro de la imagen. Del mismo modo, se ha comprobado que considerar la aberración del segundo difractóme-tro indifractóme-troduce un efecto global de disminución del valor de los picos de correlación, independientemente de la posición de la escena en la imagen, al igual que en suced´ıa en el análisis del JTC.

Por último, se ha analizado el efecto de la aberración conjunta de ambos difractóme-tros en la correlación final. En este caso, la influencia de la aberración del primer difractómetro genera varianza espacial, de manera que posiciones más alejadas del eje óptico, y por lo tanto, con valores más altos de aberración, equivalen a altura de picos de correlación menores, mientras que, al mismo tiempo, la aberración del segundo difractómetro provoca un descenso generalizado en la altura de los picos de correlación, tanto más acusado cuanto mayor es la aberración del sistema. Por otra parte, cabe destacar que el filtro adaptado mantiene una cierta robustez a la influencia de la aberración, con valores superiores al 40 % incluso en las situaciones más desfavorables, mientras que el filtro inverso y el de fase resultan especialmente sensibles a esta influencia, con valores inferiores incluso al 10 %.

Dependencia de la correlación con la posición relativa de los moduladores respecto de los sistemas ópticos

Se ha calculado la variación de los picos de correlación a medida que se modifica la distancia entre ambos moduladores y los sistemas ópticos. Se ha comprobado cómo, para los dos moduladores, la altura de los picos aumenta a medida que se reduce la distancia entre estos y los sistemas ópticos. Esta variación es más pronunciada para los filtros adaptado y de fase, mientras que no resulta tan evidente al considerar el filtro inverso, pues en este caso la variación en la altura de los picos es sensiblemente menor. Se ha analizado la evolución de la aberración de cada difractómetro para cada uno de los plano considerados anteriormente, y se ha comprobado cómo las aberraciones del primer y del segundo difractómetro se reducen a medida que, manteniendo constante

(38)

la distancia entre ambos moduladores, estos se aproximan a los sistemas ´opticos.

Diseño de filtros adaptados a las aberraciones de los sistemas difractivos. El cálculo del polinomio de aberración ha permitido incluirlo en el diseño de filtros. De este modo, se han generado filtros a partir de la imagen ideal, incluyendo infor-mación sobre la aberración del primer difractómetro, sobre la aberración del segundo difractómetro, o bien filtros que incorporan la información sobre la aberración de ambos difractómetros. Se han calculado las correlaciones correspondientes utilizan-do los conjuntos de filtros anteriores. Del análisis de los resultautilizan-dos se concluye que incorporar la información de la aberración al diseño de los filtros elimina su efecto en la correlación, de manera que se recuperan los valores correspondientes a efectuar la correlación en el caso ideal, considerando el correlador libre de aberración. Ahora bien, dado que los filtros se han generado a partir de la imagen centrada, se mantiene la variación en la altura de los picos a medida que desplazamos la escena por el plano de entrada.

Dise˜no de un correlador de VanderLugt ´optimo

A partir del diseño inicial, con correlaciones similares en ambos difractómetros, y una vez realizados los estudios anteriores, se ha propuesto una configuración alternativa, manteniendo los sistemas ópticos, los dispositivos optoelectrónicos y el factor de esca-la. Se han calculado los picos de correlación para este nuevo diseño, utilizando tanto filtros generados a partir de la imagen ideal como filtros generados incorporando la información sobre la aberración de los difractómetros. Incluso en las condiciones más desfavorables (filtros más sensibles, como el inverso y el de fase, escena afectada por mayores valores de aberración, y filtro generado a partir de la imagen sin aberrar), la altura de los picos se sitúa por encima del 60 % respecto del valor calculado para el correlador ideal, libre de aberración. En el caso más favorable (escena centrada en el plano de entrada y filtro generado con la información relativa a la aberración de ambos difractómetros) se recupera el valor máximo (100 %), correspondiente al caso ideal, para los tres filtros considerados.

(39)