Modello analitico 2

(1)

Modello analitico

La dinamica di un satellite è classicamente modellata nelle ipotesi di moto Kepleriano [13]. Nella realtà l’azione di varie fonti perturbative determina significative differenze tra l’orbita predetta dal modello kepleriano e quella effettiva tracciata dal veicolo. Per ridurre tali discrepanze, sono generalmente impiegati modelli semi-‐analitici che tengono conto delle fondamentali accelerazioni di disturbo agenti sul satellite oppure metodi di integrazione numerica delle equazioni di moto perturbate [17]. Nel seguito saranno introdotte le equazioni planetarie di Lagrange nel caso di orbita ellittica e di orbita circolare al fine di trovare le equazioni delle variazioni secolari degli elementi orbitali. Saranno poi descritte le accelerazioni dovute alle perturbazioni naturali e alla spinta del propulsore elettrico. Queste accelerazioni modificano i parametri orbitali, cioè il semiasse maggiore a,

(2)

l’eccentricità e, l’inclinazione i, l’ascensione retta del nodo ascendente Ω e l’argomento del perigeo ω.

2.1 Moto kepleriano ed elementi orbitali classici

Il modello kepleriano fa riferimento ad una condizione ideale in cui i corpi celesti si muovono come un insieme di punti materiali sottoposti all’unica forza di gravità. Il moto dei corpi celesti, riferito al Sistema Solare, è descritto dalle tre leggi di Keplero [17]:

I. L’orbita di ciascun pianeta è un’ellisse ed il Sole occupa un fuoco.

II. La congiungente pianeta-‐Sole spazza aree uguali in tempi uguali.

III. Il quadrato del periodo di ogni pianeta è proporzionale al cubo della distanza media del pianeta dal Sole.

L’equazione del moto di un corpo secondario (e.g. satellite) rispetto a un corpo primario (e.g. pianeta), trascurando l’effetto di altri corpi celesti tenendo conto solo della forza di gravità è espressa dall’Eq. 2:

𝒓 = −𝐺(𝑀 + 𝑚)

𝑟! 𝒓

(2)

(3)

dove r rappresenta la posizione del corpo secondario di massa m rispetto al corpo primario di massa M. Poiché il corpo primario ha una massa molto più grande di quella secondario, si ha che:

𝑀 + 𝑚 ≈ 𝑀 (3)

e introducendo il parametro gravitazionale relativo al corpo primario μ, espresso come:

𝜇 = 𝐺𝑀 (4)

L’Equazione del moto diventa:

𝒓 = − 𝜇

𝑟!𝒓 (4)

L’Equazione 4 descrive il problema dei due corpi.

La posizione di un satellite è individuata dalla definizione di sei grandezze scalari, che rispetto a un sistema di riferimento Geocentrico-‐ Equatoriale prendono il nome di elementi orbitali. Cinque servono per determinare le caratteristiche dell’orbita e il suo orientamento nello spazio, il sesto elemento serve per determinare la posizione del satellite lungo la propria orbita [17]. Gli elementi orbitali sono:

• a = semiasse maggiore (r per il caso di orbite circolari) • e = eccentricità (nulla per orbite circolari)

(4)

• i = inclinazione

• Ω = ascensione retta del nodo ascendente (RAAN) • ω = argomento del perigeo

• ν = anomalia vera

2.2 Equazioni di moto perturbato

Nelle ipotesi di satellite di massa m approssimato a un punto materiale, in orbita attorno a un corpo celeste (primario) avente parametro gravitazionale μ, la risultante delle forze F agenti sul centro di massa del satellite è data dalla relazione [17]:

𝑭 =𝑚 𝜇 𝑟! 𝒓 + 𝑭!! ! !!! (5a)

Dove r rappresenta il vettore posizione nel sistema di riferimento RTN (vedi Fig. 6) del satellite all’istante t, il primo termine a secondo membro modella l’attrazione gravitazionale del primario supposto a simmetria sferica e 𝑭!! è l’i-‐esima delle n forze perturbative agenti sul satellite.

Dividendo ambo i membri dell’Eq.4 per la massa m l’equazione di moto perturbato del satellite risulta [17].:

(5)

𝑭 𝑚= 𝜇 𝑟!𝒓 + 𝒂!! ! !!! (5b)

dove il termine 𝒂_!_! rappresenta l’i-‐esima forza perturbativa per unità di massa, e quindi un’accelerazione perturbativa.

Le principali accelerazioni perturbative agenti sul veicolo sono tradizionalmente modellate nel sistema di riferimento RTN, la cui origine coincide, istante per istante, con il baricentro del satellite e i cui versori sono !_!, !_!, !_!. Il versore !_! è diretto lungo la radiale locale e punta verso l’esterno rispetto al primario, !_! è perpendicolare al piano orbitale istantaneo ed è concorde con il momento della quantità di moto

h e !_! giace nel piano di moto istantaneo ed è concorde con il vettore velocità v (vedi Fig.6).

(6)

Figura 6 -‐ Definizione del sistema di riferimento RTN [15]

A causa delle accelerazioni perturbative gli elementi orbitali classici variano nel tempo, subendo delle variazioni espresse come la differenza fra il valore finale e il valore iniziale del parametro orbitale, come illustrato nelle Eq.6:

𝛥𝑎 = 𝑎!− 𝑎! 𝛥𝑒 = 𝑒!− 𝑒! 𝛥𝑖 = 𝑖_!− 𝑖_! 𝛥𝛺 = 𝛺_!− 𝛺_! 𝛥𝜔 = 𝜔_!− 𝜔_! (6)

(7)

dove 𝛥𝑎, 𝛥𝑒, 𝛥𝑖, 𝛥𝛺, 𝛥𝜔 sono rispettivamente le variazioni del semiasse maggiore, dell’eccentricità, dell’inclinazione, dell’ascensione retta del nodo ascendente e dell’argomento del perigeo. Col pedice f si indicano i valori finali degli elementi orbitali mentre col pedice i i valori iniziali.

Considerando un metodo diretto, come quello descritto da P. H. Cowell [18], l’integrazione del valore dell’accelerazione di perturbazione per tempo lunghi potrebbe essere molto costoso in termini di tempo di calcolo. Una soluzione alternativa a questo problema è l’implementazione del metodo di Encke [18], applicabile fin tanto che l’errore di propagazione rimanga piccolo. Data l’instabilità numerica e la perdita di precisione si preferisce non utilizzare questo metodo [19]. Le equazioni planetarie di Lagrange in forma gaussiana [13], rappresentano un’ulteriore alternativa per modellare gli effetti di perturbazione. Tali equazioni saranno descritte nel paragrafo successivo.

2.3 Equazioni planetarie di Lagrange

Le equazioni planetarie di Lagrange, in forma gaussiana, esprimono l’evoluzione nel tempo dei parametri orbitali classici sotto l’effetto di perturbazioni non conservative e sono [13]:

(8)

𝑑𝑎 𝑑𝑡 = 2 𝑎! 𝜇(1 − 𝑒!₎ 𝑒 sin 𝜈 𝑎!"+ 1 + 𝑒 cos 𝜈 𝑎!" (7) 𝑑𝑒 𝑑𝑡 = 𝑎(1 − 𝑒!₎

𝜇 sin 𝜈 𝑎!" + cos 𝐸 + cos 𝜈 𝑎!" 𝑑𝑖 𝑑𝑡= 𝑎(1 − 𝑒!₎ 𝜇(1 + 𝑒 cos 𝜈)cos 𝑢 𝑎!" 𝑑𝛺 𝑑𝑡 = 𝑎(1 − 𝑒!_{) sin 𝑢} 𝜇(1 + 𝑒 cos 𝜈) sin 𝑖𝑎!" 𝑑𝜔 𝑑𝑡 = 𝑎(1 − 𝑒!₎ 𝜇 − sin 𝑢 cot 𝑖 1 + 𝑒 cos 𝜈𝑎!!+ 2 + 𝑒 cos 𝜈 𝑒 (1 + 𝑒 cos 𝜈)sin 𝜈 𝑎!" −cos 𝜈 𝑒 𝑎!"

dove ν è l’anomalia vera, u è l’argomento della latitudine, 𝑎_!_!, 𝑎_!" e 𝑎_!" sono rispettivamente la componente normale, circonferenziale e radiale della risultante delle accelerazioni di perturbazione nel sistema di riferimento RTN.

Si possono scrivere le variazioni dei parametri orbitali anche in termini di anomalia eccentrica E , una misura angolare definita come:

𝐸 = 2 arctan 1 − 𝑒 1 + 𝑒tan 𝜈 2 (8)

(9)

dove e è l’eccentricità dell’orbita e ν è l’anomali vera.

A tal fine utilizzando la relazione [17]: 𝑑𝐸 𝑑𝑡 = 1 𝑟 𝜇 𝑎 (9)

che esprime la variazione temporale dell’anomalia eccentrica, le equazioni di variazione dei parametri orbitali, si scrivono [13]:

𝑑𝑎 𝑑𝐸 = 2𝑎! 𝜇 (𝑎!"𝑒 sin 𝐸 + 𝑎!" 1 − 𝑒!) (10) 𝑑𝑒 𝑑𝐸 = 𝑎! 𝜇 [𝑎!" 1 − 𝑒! sin 𝐸 + 𝑎!" 1 − 𝑒!(2 cos 𝐸 − 𝑒 − 𝑒 𝑐𝑜𝑠!𝐸)] 𝑑𝑖 𝑑𝐸 = 𝑎! 𝜇 𝑎!"(1 − 𝑒 cos 𝐸) (cos 𝐸 − 𝑒) cos 𝜔 1 − 𝑒! − sin 𝐸 sin 𝜔 𝑑𝛺 𝑑𝐸 = 𝑎! 𝜇 𝑎!" 1 − 𝑒 cos 𝐸 sin 𝑖 cos 𝐸 − 𝑒 sin 𝜔 1 − 𝑒! + sin 𝐸 cos 𝜔 𝑑𝜔 𝑑𝐸 = 𝑎!

𝜇 𝑒[−𝑎!" 1 − 𝑒! cos 𝐸 − 𝑒 + 𝑎!" 2 − 𝑒!− 𝑒 cos 𝐸 sin 𝐸 − 𝑎!" 1 − 𝑒 cos 𝐸 cot 𝑖 [ cos 𝐸 − 𝑒 sin 𝜔 1 − 𝑒! + sin 𝐸 cos 𝜔]]

(10)

Poiché nel presente lavoro l’analisi di missione sarà condotta nell’ipotesi di orbita circolare per ogni istante di moto, ponendo e=0 nelle Eq.7 si ottengono le equazioni di variazione dei parametri orbitali nel caso di orbita circolare:

𝑑𝑎 𝑑𝑡 = 2 𝑎! 𝜇 𝑎!" (11) 𝑑𝑖 𝑑𝑡= 𝑎 𝜇cos 𝑢 𝑎!" 𝑑𝛺 𝑑𝑡 = 𝑎 sin 𝑢 𝜇 sin 𝑖𝑎!"

In particolare, per orbita circolare, l’equazione di variazione dell’argomento del perigeo non compare perché tale elemento orbitale non è definito [13]. Inoltre, per ipotesi di orbita circolare ad ogni istante di moto, nel presente lavoro saranno trascurate anche le variazioni di eccentricità. Le variazioni degli elementi orbitali in termini di anomalia eccentrica E per orbita circolare sono [13]:

𝑑𝑎 𝑑𝐸= 2𝑎! 𝜇 𝑎!" (12) 𝑑𝑖 𝑑𝐸= 𝑎!

𝜇 𝑎!" cos 𝐸 cos 𝜔 − sin 𝐸 sin 𝜔 = 𝑎!

(11)

𝑑𝛺

𝑑𝐸 =

𝑎!

𝜇 𝑎!" 1

sin 𝑖 sin 𝜔 cos 𝐸 + sin 𝐸 cos 𝜔 = 𝑎!

𝜇 𝑎!" 1

sin 𝑖sin 𝑢

Dalle Eq. 12 risulta che il semiasse maggiore subisce una variazione solo in presenza di un’accelerazione perturbativa con componente tangenziale (𝑎_!") non nulla !_!, mentre l’inclinazione e l’ascensione retta del nodo ascendente variano solo in presenza di un’accelerazione perturbativa con componente normale (𝑎_!") non nulla. Per trovare le variazioni secolari di ciascun elemento orbitale si integrano le Eq. 10 – 12 su un’intera orbita mantenendo gli altri costanti.

2.4 Principali azioni perturbative naturali considerate

Le principali azioni perturbative agenti su un satellite in orbita intorno alla Terra sono dovute a [17]:

• Resistenza atmosferica

• Asimmetria del campo gravitazionale terrestre

• Azione di attrazione gravitazionale del Sole e della Luna • Pressione di radiazione solare

In quest’analisi sarà preso in considerazione solo l’effetto della resistenza atmosferica e di J2, poiché per orbite LEO gli effetti dell’attrazione Luni-‐Solare e della pressione di radiazione solare sono trascurabili. Infatti, a tali altitudini la pressione di radiazione solare e

(12)

l’accelerazione dovuta all’attrazione Luni-‐Solare, hanno un ordine di grandezza di circa 10!!_.

2.5.3 Accelerazione perturbativa dovuta all’azione aerodinamica

L’effetto della resistenza atmosferica è la diminuzione sia del semiasse maggiore che dell’eccentricità di un’orbita ellittica [17]. Durante la “circolarizzazione” dell’orbita l’altitudine del perigeo è pressappoco costante pertanto la riduzione del semiasse maggiore dell’orbita è principalmente dovuta alla diminuzione della quota di apogeo. Raggiunta la condizione di eccentricità quasi nulla la resistenza aerodinamica determina una traiettoria a spirale con costante diminuzione della quota, fino a quando il satellite non raggiunge un’altitudine tale che la densità atmosferica è così elevata da provocarne il surriscaldamento per attrito e quindi la distruzione completa o parziale. In quest’ultimo caso i resti impatteranno con la superficie terrestre [RIF]. Per altitudini sopra i 600 km circa, a causa della scarsa densità atmosferica (~1,45 × 10!!"_{𝑘𝑔/𝑚}!_{),
l’effetto
della}

resistenza aerodinamica è quasi trascurabile [17].

Al di sotto dei 600 km di altitudine la densità dell’atmosfera risulta sufficientemente elevata (~10!!"_{𝑘𝑔/𝑚}!_{)
da
avere
effetto
significativo}

sul moto del satellite, determinandone in molti casi il deorbitamento naturale e la conseguente riduzione della vita operativa.

(13)

La risultante delle forze aerodinamica agenti sul satellite è legata principalmente a [17]:

• la forma del satellite e il suo assetto di moto (l’intensità e la direzione delle forze aerodinamiche agenti sul veicolo variano in funzione di essi);

• le caratteristiche fisiche dell’atmosfera terrestre che variano in funzione dell’altitudine e dall’attività solare e geomagnetica (ad esempio, ad altitudini particolarmente elevate l’aria non può essere considerata un mezzo continuo perché si comporta come un gas molto rarefatto);

• al grado di ionizzazione dell’atmosfera (le molecole ionizzate possono interagire con le superfici esposte del satellite).

Tale forza risultante, 𝐅_!_! , agisce nel piano dell’orbita del veicolo ed è scomponibile nella direzione parallela al vettore velocità relativa satellite-‐atmosfera (𝒗 ) e nella direzione perpendicolare a quest’ultima (𝒗_𝒑) ottenendo [17]:

𝐅_!_! = −𝐷𝒗 + 𝐿𝒗_𝒑 (13)

nella quale D è detta forza di resistenza ed L forza di portanza.

Poiché i satelliti sono considerati dei corpi tozzi, generalmente l’effetto della portanza è trascurabile rispetto a quello dovuto alla resistenza aerodinamica [20]. Quest’ultima è espressa come[17]:

(14)

𝐷 = 1

2𝑚𝜌𝐴𝑉!𝐶! (14)

in cui m è la massa del satellite, A è l’area media della sezione trasversale del satellite nella direzione del moto, V è il modulo della velocità orbitale, ρ è la densità locale dell’aria e 𝐶_! è il coefficiente di resistenza.

L’accelerazione perturbativa dovuta all’azione aerodinamica è quindi: 𝑎! = − 1 2𝜌𝐶!𝐴 𝑉! 𝑚 (15)

e può essere scomposta nella direzione tangenziale:

𝒂_!" = −𝐷 cos 𝛾 !_! (16)

e in quella radiale:

𝒂!" = −𝐷 sin 𝛾 !! (17)

nelle quali γ è l’angolo di traiettoria, definito come:

𝛾 = 𝑠𝑖𝑔𝑛 𝒓 • 𝒗 arccos _{𝑟 𝑣}ℎ (18)

dove h è il momento della quantità di moto, r e v rappresentano rispettivamente il vettore posizione e il vettore velocità.

(15)

Al fine di ricavare la variazione secolare degli elementi orbitali generata dalla resistenza atmosferica si sostituiscono le espressioni per le componenti di accelerazione (Eq.16 e 17) nelle equazioni di Lagrange per un’orbita circolare (Eq. 12) ottenendo [13]:

𝑑𝑎 𝑑𝐸= − 2𝑎! 𝜇 𝐷 = − 𝑎!_𝜌𝐴𝐶 ! 𝑚 (19)

Integrando l’Eq. 19 su un’intera orbita, ovvero per E tra 0 e 2π, si ottiene la variazione secolare del semiasse maggiore Δa dovuta alla resistenza atmosferica [13]: ∆𝑎 = −𝑎!𝜌𝐴𝐶! 𝑚 𝑑𝐸 !! ! = −𝑎!𝜌𝐴𝐶! 𝑚 2𝜋 (20)

L’Eq. 19 è ricavata nell’ipotesi semplificativa di densità atmosferica ρ costante lungo l’intera orbita. Per semplificare il problema, nel presente lavoro si ipotizza la densità atmosferica costante su un’orbita ma variabile da orbita circolare a orbita circolare in funzione dell’altitudine. Il segno meno nell’Eq. 20 indica che il semiasse maggiore dell’orbita diminuisce, determinando la perdita di quota del satellite.

La resistenza atmosferica non provoca, invece, alcuna variazione secolare d’inclinazione e di RAAN perché esse dipendono entrambe solo dalla presenza di un’accelerazione perturbativa diretta lungo la direzione normale !_! (vedi Eq.12)

(16)

2.5.2 Asimmetria del campo gravitazionale terrestre

A causa dell’effetto provocato dalla non perfetta sfericità della Terra, ovvero dall’asimmetria del geopotenziale ed in particolare dell’armonica zonale J2, essendo due ordini di grandezza maggiore rispetto a tutte le altre, il piano orbitale del satellite subisce una rotazione attorno all’asse polare della Terra, che si traduce in una continua rotazione (precessione) della linea dei nodi [22], producendo una variazione secolare dell’ascensione retta del nodo ascendente e dell’argomento del perigeo.

Una delle perturbazioni di maggior interesse per satelliti in orbite LEO è quella dovuta alla non perfetta sfericità del campo gravitazionale terrestre. È noto che la distribuzione di massa della Terra non è perfettamente sferica e la densità non è uniforme [22], quindi la superficie equipotenziale del campo gravitazionale terrestre non è una sfera, bensì un geoide (vedi Fig. 7).

Il geoide è la superficie che meglio di qualunque altra approssima la forma geometrica della Terra, però risulta pressoché inutilizzabile per il calcolo del campo gravitazionale a causa della sua eccessiva irregolarità [22]. La figura geometrica più semplice che meglio approssima il geoide è l’ellissoide di rotazione biassiale. Quindi, al fine di evitare le notevoli

(17)

complicazioni derivanti dall’uso del geoide nel calcolo del campo gravitazionale, è ragionevole schematizzare la forma geometrica della Terra con un ellissoide il cui raggio equatoriale è più grande di quello polare. Grazie a questa approssimazione, si può ottenere un modello semi-‐analitico del potenziale gravitazionale in un generico punto esterno all’ellissoide, come [17]:

𝑈 =𝐺 𝑀! 𝑟 [1 − 𝐽! 𝑅_! 𝑟 ! 𝑃_!(sin 𝛿) ! !!! ] (21)

nella quale r è la distanza del punto dal centro di massa della Terra, 𝑀_! e 𝑅! sono rispettivamente la massa e il raggio equatoriale della Terra, δ

è la declinazione del punto, 𝑃_!(sin 𝛿) rappresenta il polinomio di Legendre di ordine n in (sin δ), ed infine 𝐽_! sono delle costanti chiamate

armoniche zonali.

L’armonica zonale che produce un effetto più significativo è 𝐽_! perché è dell’ordine di 10!!_{,
mentre
le
altre
di
10}!!_{o
di
entità
inferiore;
si
può}

quindi riscrivere il potenziale gravitazionale relativo solo a quest’ultima [17]: 𝑈_!_! = − 𝜇 𝑟𝐽! 𝑅 𝑟 ! ₃ 2𝑠𝑖𝑛!𝛿 − 1 2 (22)

Calcolando il gradiente del potenziale gravitazionale in Eq. 22 si ottiene l’espressione finale dell’accelerazione di perturbazione dovuta a 𝐽_! [17]:

(18)

𝒂_𝑱_𝟐 = −𝜇𝐽_!𝑅! 3 𝑟! 1 2− 3 2𝑠𝑖𝑛!𝑖 𝑠𝑖𝑛!𝑢 𝒊𝑹− 𝑠𝑖𝑛!𝑖 sin 𝑢 cos 𝑢 𝒊𝑻 + cos 𝑖 sin 𝑖 sin 𝑢 𝒊_𝑵

(23)

Diversamente dal vettore accelerazione relativo alla resistenza aerodinamica (Eq. 15), il vettore accelerazione relativo all’effetto di 𝐽_! possiede tutte e tre le componenti: radiale, tangenziale e normale.

Sostituendo l’espressione ottenuta per l’accelerazione perturbativa (Eq.23) nelle equazioni di perturbazione relative al caso di orbita circolare (Eq.12) si giunge alle seguenti relazioni[RIF]:

𝑑𝑎 𝑑𝐸= − 2 3𝑟!𝑎!𝐽!𝑅! 𝑠𝑖𝑛!𝑖 1 2sin 2𝑢 (24) 𝑑𝑖 𝑑𝐸= 𝑎! 𝜇 −𝜇𝐽!𝑅! 3

𝑟! cos 𝑖 sin 𝑖 sin 𝑢 cos 𝐸 cos 𝜔

− sin 𝐸 sin 𝜔 𝑑𝛺 𝑑𝐸 = 𝑎! 𝜇 1 sin 𝑖 −𝜇𝐽!𝑅! 3

𝑟! cos 𝑖 sin 𝑖 sin 𝑢 cos 𝐸 sin 𝜔

+ sin 𝐸 cos 𝜔

Per ricavare le variazioni secolari dei tre parametri orbitali si effettua l’integrazione delle Eq.24 su un’intera orbita, giungendo ai risultati seguenti:

(19)

∆𝑎 = −𝑠𝑖𝑛!𝑖 3𝑟 𝐽!𝑅! !! ! sin 2𝑢 𝑑𝐸 = −𝑠𝑖𝑛!𝑖 3𝑟 𝐽!𝑅! sin 2𝐸 𝑑𝐸 !! ! = 0 (25) ∆𝑖 = 3𝐽!𝑅! 4𝑟! sin 2𝑖 sin 2𝑢 𝑑𝐸 !! ! =3𝐽!𝑅! 4𝑟! sin 2𝑖 sin 2𝐸 𝑑𝐸 !! ! = 0 ∆𝛺 = −3𝐽!𝑅! 𝑟! cos 𝑖 𝑠𝑖𝑛!𝑢 𝑑𝐸 !! ! = −3𝐽!𝑅! 𝑟! cos 𝑖 𝑠𝑖𝑛!𝐸 !! ! 𝑑𝐸 = −3𝜋𝐽_𝑟!_!𝑅!cos 𝑖

Si nota che l’unico parametro orbitale a subire una variazione secolare a causa dell’asimmetria del campo gravitazionale terrestre è l’ascensione retta del nodo ascendente.

2.5 Modellazione della spinta

Poiché nella realtà si ha a disposizione una spinta finita e non infinita, sorge il problema di determinare le condizioni secondo le quali l’approssimazione di manovra impulsiva è accettabile, e quando è invece necessario ricorrere a un modello più preciso e complicato. In accordo con la teoria di Chobotov [13], poiché non è possibile definire una netta distinzione fra un livello “alto” e uno “basso” di spinta, si ricorre al valore del rapporto spinta/peso per quantificare, in modo approssimato, l’entità della spinta fornita dal propulsore. Il rapporto spinta/peso rappresenta il rapporto tra il modulo della spinta (T)e il peso locale (𝑊_! ) del veicolo spaziale calcolato come [17]:

(20)

𝑊_! = 𝑚 𝜇

𝑟! (26)

in cui m è la massa istantanea del veicolo e r è la sua distanza dal centro di massa del corpo primario, avente un parametro gravitazionale μ.

Se (T/𝑊!)≥0.5 la spinta è definita alta. In questo caso la spinta del

propulsore è il termine dominante rispetto a 𝑊_!, quindi la manovra può essere considerata, in prima analisi, impulsiva. Se invece (T/𝑊!)≤10!!,

la spinta è detta bassa e in tal caso per ottenere una variazione significativa dei parametri orbitali è necessario che agisca in modo continuo per un lungo intervallo temporale. Inoltre, la spinta in quest’ultimo caso è talmente bassa che può essere trattata alla stregua di una perturbazione orbitale, così da poter utilizzare le equazioni di Lagrange e ottenere modelli semi-‐analitici per lo studio del moto propulso.

Poiché in questo lavoro, il satellite utilizza un motore a propulsione elettrica, la spinta è talmente bassa (~10!!_{N)che
può
essere
trattata}

come una perturbazione orbitale.

2.5.2 Accelerazione di perturbazione dovuta al motore

Al fine di utilizzare le Equazioni di Lagrange in forma di Gauss, Eq.10, anche per la determinazione della variazione dei parametri orbitali per

(21)

effetto di una bassa spinta, è necessario calcolare le tre componenti del vettore accelerazione di spinta nel sistema RTN.

In Fig. 8 è rappresentata la scomposizione del vettore accelerazione di spinta 𝒂! (in rosso) lungo le tre direzioni del sistema di riferimento

RTN (𝒂_!_!, 𝒂_!_! e 𝒂_!_! ). Il vettore 𝒂_!_!" , tratteggiato in rosso, giace sul piano orbitale osculante ed è la risultante delle componenti radiale e tangenziale del vettore di accelerazione.

Figura 8 -‐ Componenti del vettore accelerazione di spinta nel sistema di riferimento RTN.

(22)

Figura 9 – Definizione degli angoli di spinta.

In Figura 9 sono illustrati gli angoli γ e β, detti angoli di spinta, che rappresentano rispettivamente l’angolo compreso tra i vettori 𝒂_!_! e 𝒂_!_!" e l’angolo compreso tra i vettori 𝒂_! e 𝒂_!_!" . Tali angoli permettono di individuare la direzione del vettore accelerazione di spinta nel sistema di riferimento RTN. Infatti, le tre componenti del vettore accelerazione di spinta nel sistema RTN possono essere espresse in funzione di γ e β secondo le relazioni:

𝑎!! = 𝑎!!"cos 𝛾 = 𝑎!cos 𝛽 cos 𝛾

(27)

𝑎_!_!= 𝑎_!_!"sin 𝛾 = 𝑎_!cos 𝛽 sin 𝛾

(23)

2.5.2 Variazioni dei parametri orbitali per effetto della spinta

Sostituendo le espressioni delle componenti dell’accelerazione di spinta (Eq. 27) all’interno delle equazioni planetarie di Lagrange (Eq.10) si ottengono le variazioni dei parametri orbitali dovute alla spinta [23]:

𝑑𝑎

𝑑𝐸=

2𝑎!

𝜇 (𝑎!cos 𝛽 sin 𝛾 𝑒 sin 𝐸 + 𝑎!cos 𝛽 cos 𝛾 1 − 𝑒!)

(28) 𝑑𝑒

𝑑𝐸=

𝑎!

𝜇 [𝑎!cos 𝛽 sin 𝛾 1 − 𝑒! sin 𝐸

+ 𝑎!cos 𝛽 cos 𝛾 1 − 𝑒!(2 cos 𝐸 − 𝑒 − 𝑒 𝑐𝑜𝑠!𝐸)]

𝑑𝑖 𝑑𝐸= 𝑎! 𝜇 𝑎!sin 𝛽 (1 − 𝑒 cos 𝐸) (cos 𝐸 − 𝑒) cos 𝜔 1 − 𝑒! − sin 𝐸 sin 𝜔 𝑑𝛺 𝑑𝐸 = 𝑎! 𝜇 𝑎!sin 𝛽 1 − 𝑒 cos 𝐸 sin 𝑖 cos 𝐸 − 𝑒 sin 𝜔 1 − 𝑒! + sin 𝐸 cos 𝜔 𝑑𝜔 𝑑𝐸 = 𝑎!

𝜇 𝑒[−𝑎!cos 𝛽 sin 𝛾 1 − 𝑒! cos 𝐸 − 𝑒

+ 𝑎_!cos 𝛽 cos 𝛾 2 − 𝑒!_{− 𝑒 cos 𝐸 sin 𝐸}

− 𝑎_!sin 𝛽 1 − 𝑒 cos 𝐸 cot 𝑖 [ cos 𝐸 − 𝑒 sin 𝜔

1 − 𝑒! + sin 𝐸 cos 𝜔]]

(24)

Integrando le Eq.28 su un’intera orbita, nell’ipotesi che l’angolo γ rimanga costante, si ottengono le espressioni delle variazioni secolari dei cinque parametri orbitali seguenti [23]:

∆𝑎 =4𝑎!𝑎!cos 𝛽 (𝜋 cos 𝛾 1 − 𝑒!+ 2𝑒 sin 𝛾)

𝜇

(29) ∆𝑒 = 𝑎!𝑎!_𝜇cos 𝛽[4 sin 𝛾 1 − 𝑒! _{+ 1 − 𝑒}!_{cos 𝛾 8 − 3𝜋𝑒 ]}

∆𝑖 =𝑎!𝑎!sin 𝛽 𝜇 1 − 𝑒! 4 + 4𝑒 !_{− 3𝜋𝑒 cos 𝜔 + 2 𝑒 − 2 1 − 𝑒}!_{sin 𝜔} ∆𝛺 = 𝑎!𝑎!sin 𝛽 𝜇 1 − 𝑒!_{sin 𝑖} 4 + 4𝑒 !_{− 3𝜋𝑒 sin 𝜔} + 2 𝑒 − 2 1 − 𝑒!_{cos 𝜔} ∆𝜔 = − 𝑎!𝑎!

𝑒𝜇 1 − 𝑒! e sin 𝛽 cot 𝑖 sin 𝜔 4 + 4𝑒

!_{− 3𝜋𝑒} + 2 1 − 𝑒!_{cos 𝜔 2 − 𝑒} + cos 𝛽[ 2 1 − 𝑒!_{cos 𝛾 𝑒 − 4 + 2𝑒}! + 2 sin 𝛾 𝑒!_{− 1 (𝜋𝑒 − 2)]}

Ipotizzare che l’angolo γ rimanga costante su un’intera orbita è solo un’approssimazione semplificativa. Infatti, γ, in realtà, dipende esplicitamente dall’anomalia eccentrica E e dall’eccentricità, come espresso dalle seguenti relazioni [24]:

(25)

sin 𝛾 = 𝑒 sin 𝐸 1 − 𝑒 cos 𝐸 1 + 𝑒𝑐𝑜𝑠 𝐸 (30) cos 𝛾 = 1 − 𝑒! 1 − 𝑒 cos 𝐸 1 + 𝑒𝑐𝑜𝑠 𝐸

Specificando le Eq. 28 per il caso di orbita circolare (e=0, cos 𝛾 = 1 e sin 𝛾 = 0) si ottengono le variazioni secolari dei parametri orbitali a, i e

Ω che saranno utilizzate nel presente lavoro.

In particolare, la variazione istantanea del semiasse maggiore di un’orbita circolare risulta:

𝑑𝑎 𝑑𝐸= 2𝑎!_𝑎 !! 𝜇 (31)

ed integrando su un’orbita, ovvero per E tra 0 e 2π, si ottiene la variazione secolare di 𝑎:

∆𝑎 = 2𝑎!𝑎!! 𝜇 𝑑𝐸 !! ! =4𝜋𝑎!𝑎!! 𝜇 = 4𝜋𝑎! 𝜇 𝑎!cos 𝛽 cos 𝛾 (32)

Poiché per orbita circolare cos 𝛾=1 l’Eq.32 diventa infine:

∆𝑎_!"#"$% =4𝜋𝑟!

𝜇 𝑎!cos 𝛽 (33)

(26)

nella quale r è il raggio orbitale.

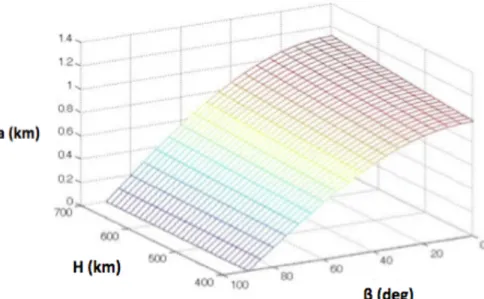
Analizzando l’andamento di Δa in funzione di r e β, è possibile ottenere per quali valori di β, compresi tra 0 e 90°, Δa assume valore massimo o minimo fissato il raggio orbitale. In Figura 10 è rappresentato l’andamento di Δa in funzione dell’altitudine H e β per valori di altitudine compresi tra 400 e 35000 km. Tali dati sono ottenuti prendendo in considerazione un satellite di massa pari a 1000 kg e 100 mN di spinta. In Figura 11 è raffigurato l’andamento di Δa nelle stesse ipotesi ma considerando un intervallo di altitudini più ristretto, compreso tra 400 e 700 km.

Figura 10 -‐ Andamento di Δa in funzione dell’angolo β e dell’altitudine H (400 km<H<35000 km).

(27)

Figura 11 -‐ Andamento di Δa in funzione dell’angolo β e dell’altitudine H (400 km<𝑯<700 km)

Analizzando la Fig.10 è risulta che indipendentemente dall’altitudine valori di β prossimi allo zero danno una maggiore variazione del semiasse rispetto a quelli prossimi a 90°. Tale differenza risulta più marcata all’aumentare dell’altitudine. Inoltre, per ogni valore di β maggiore è la quota dell’orbita, maggiore è la variazione di Δa. Il massimo valore di Δa nel grafico corrisponde all’orbita con altitudine di 35000 km ed è dell’ordine di centinaia di chilometri. In Figura 11 si nota come la variazione del semiasse maggiore cambi dell’ordine di qualche centinaia di metri per valori di altitudine inferiore a 700 km e valori di β pari a 0.

(28)

Per valori diversi da zero, l’angolo di spinta β provoca anche cambiamenti di inclinazione e di RAAN, come sarà mostrato nel seguito del paragrafo.

La variazione d’inclinazione dovuta all’effetto della spinta è data da: 𝑑𝑖 𝑑𝐸= 𝑎! 𝜇 𝑎!!cos 𝐸 𝑑𝑖 𝑑𝐸 = 𝑎!

𝜇 𝑎!! cos 𝐸 cos 𝜔 − sin 𝐸 sin 𝜔 =𝑎!

𝜇 𝑎!!cos 𝑢

(34)

ottenuta tenendo in considerando il fatto che per un’orbita circolare:

cos 𝑢 = cos(𝜔 + 𝐸) ≅ cos 𝐸 𝑑𝑖

𝑑𝐸 =

𝑎!

𝜇 𝑎!!cos 𝐸 (35)

Poiché, in generale integrando l’Eq.34 fra 0 e 2π il risultato sarebbe zero, è necessario adottare una strategia di spinta opportuna che permetta di ottenere una variazione secolare d’inclinazione diversa da zero. Si sceglie una strategia di spinta normale che permetta di ottenere una pura variazione di inclinazione su un’orbita, ovvero che non determini variazione secolare di RAAN. Tale strategia consiste nell’invertire il verso della componente normale della spinta in due punti dell’orbita, a E=π/2 e E=-‐π/2, e permette di ottenere la variazione massima possibile di inclinazione su un’orbita:

(29)

∆𝑖_!"#"$% = 𝑎! 𝜇 𝑎!!cos 𝑢 𝑑𝐸 !! ! = 𝑎! 𝜇 𝑎!sin 𝛽 cos 𝐸 !! ! 𝑑𝐸 =2 𝑎! 𝜇 𝑎!sin 𝛽 cos 𝐸 𝑑𝐸 ! ! !!_! =4𝑟! 𝜇 𝑎!sin 𝛽 (36)

dove r indica il raggio orbitale iniziale supposto invariabile.

In Figura 12 è mostrato il grafico dell’andamento di Δi in funzione di r e

β per altitudini comprese fra 400 km e 35000 km. Diversamente dal

caso precedente, il massimo valore della variazione di inclinazione si ottiene per β uguale a zero, specialmente alle quote vicine a quella dell’orbita GEO. La Fig. 13, invece, mostra l’andamento di Δi per altitudini comprese fra 400 km e 700 km, dove le variazioni sono dell’ordine di 10!! _{gradi.
Tali
dati
sono
ottenuti
prendendo
in}

considerazione un satellite di massa pari a 1000 kg e 100 mN di spinta

Figura 12 – Andamento di Δi in funzione dell’altitudine 𝑯 (400 km<𝑯<35000 km) e dell’angolo β.

(30)

Figura 13 – Andamento di Δi in funzione dell’altitudine 𝑯 (400 km<𝑯<35000 km) e dell’angolo β.

L’accelerazione di perturbazione per il caso di orbita circolare determina una variazione di RAAN espressa da:

𝑑𝛺 𝑑𝐸 = 𝑎! 𝜇 1

sin 𝑖𝑎!! cos 𝐸 sin 𝜔 + sin 𝐸 cos 𝜔 = 𝑎!

𝜇 1

sin 𝑖𝑎!!sin 𝑢 (37)

Considerando un’orbita circolare (vedi Eq. 35) si ottiene la relazione: 𝑑𝛺 𝑑𝐸 = 𝑎! 𝜇 1 sin 𝑖𝑎!!sin 𝐸 (38)

Anche in questo caso al fine di ottenere una variazione secolare di RAAN non nulla è necessario adottare una specifica strategia di spinta

(31)

normale. Si sceglie di invertire la componente normale della spinta in due punti dell’orbita a E=π e E=0, ciò permetta di ottenere una pura variazione di inclinazione su un’orbita, ovvero che non determina variazione secolare di inclinazione:

∆𝛺_!"#"$% = 𝑎! 𝜇 1 sin 𝑖𝑎!!sin 𝑢 𝑑𝐸 !! ! =𝑎! 𝜇 1

sin 𝑖𝑎!sin 𝛽 sin 𝐸

!! ! 𝑑𝐸 =2 𝑎! 𝜇 1

sin 𝑖𝑎!sin 𝛽 sin 𝐸

! ! 𝑑𝐸 =𝑟! 𝜇 4 sin 𝑖𝑎!sin 𝛽 (38)

dove r è il raggio orbitale iniziale supposto costante. Si noti che l’Eq. 38 non è utilizzabile nel caso di orbite equatoriali, infatti per esse il RAAN non è definito.

Dato che ΔΩ dipende da r, i e β, per studiarne l’andamento sono stati fissati arbitrariamente due diversi valori di inclinazione, 20° e 80°, e per ognuno la variazione di ΔΩ in funzione di r e β è stata analizzata. In Figura 14 tali andamenti per altitudini comprese tra 400 e 35000 km sono rappresentati con due superfici corrispondenti ai due diversi casi di inclinazione analizzati. Il grafico relativo all’inclinazione di 20° mostra variazioni secolari di RAAN maggiori, perché, da come si nota nell’Eq.38, il ΔΩ dipende dall’inverso del seno dell’inclinazione; quindi minore è l’inclinazione dell’orbita maggiori sono le variazioni di RAAN. La Figura 15 mostra grafici analoghi nel caso di altitudini comprese fra

(32)

400 e 700 km. Tali dati sono ottenuti prendendo in considerazione un satellite di massa pari a 1000 kg e 100 mN di spinta.

Figura 14 – Andamenti di ΔΩ in funzione dell’altitudine 𝑯 (400 km<𝑯<35000 km) e dell’angolo β; il grafico superiore è relativo a un’inclinazione di 20°,

(33)

Figura 15 -‐ Andamenti di ΔΩ in funzione dell’altitudine 𝑯 e β (400 km<𝑯<700 km); il grafico superiore è relativo a un’inclinazione di 20°, mentre quello

inferiore a una di 80°.

2.5.3 L’angolo β

Dallo studio degli andamenti delle variazioni per rivoluzione dei tre elementi orbitali a, i e RAAN, è possibile dedurre i valori dell’angolo di sparo fuori dal piano (β) per i quali è massima la variazione secolare di ciascun elemento. Il massimo Δa è ottenibile per β=0°. In tal caso Δi e

ΔΩ sono entrambi nulli (Eq. 35). La massima variazione secolare di

inclinazione o di ascensione retta per le strategie di sparo specificate è data da β=90°. In tal caso Δa è nullo in quanto la componente di accelerazione di spinta nel piano istantaneo di moto è nulla. Chiaramente questi valori di β possono essere usati solo ed

(34)

esclusivamente se si vuole ottenere, singolarmente, un cambio di semiasse maggiore, un cambio di inclinazione oppure un cambio di

RAAN. Al fine di ottenere una contemporanea variazione di semiasse

maggiore e di inclinazione dell’orbita oppure di semiasse maggiore e di RAAN è necessario selezionare valori dell’angolo di sparo β diversi da 0 e da 90°.

La selezionata strategia di spinta su un’orbita per ottenere Δi è caratterizzata dall’inversione della componente normale della spinta a E= ±π/2. Ciò si traduce nel cambiamento di segno dell’angolo β all’attraversamento di uno dei due valori dell’anomalia eccentrica E. Quindi, il propulsore è supposto sparare per metà orbita in una direzione fuori dal piano orbitale, mentre per l’altra metà nella direzione opposta. Per quanto riguarda ΔΩ la strategia di spinta è analoga, ma i due archi di circonferenza sono compresi fra 0 e π. Risulta quindi che non è possibile ottenere contemporaneamente un cambiamento di inclinazione e uno di RAAN, mentre è possibile modificare contemporaneamente il semiasse maggiore e l’inclinazione o il semiasse maggiore e il RAAN.

Nel presente lavoro siamo interessati ad analizzare missioni di trasferimento da un’orbita circolare all’altra utilizzando le strategie di sparo descritte. Sarà, quindi, necessario determinare l’andamento temporale dell’angolo di sparo β durante l’intero trasferimento. L’angolo γ è fissato uguale a zero ad ogni istante in quanto non influenza le variazioni secolari di Δi e ΔΩ e la strategia di sparo tangenziale è quella che massimizza Δa [15] .

(35)

Combinando le Eq. 33 – 35 – 38 la relazione che esprime β per cambiamenti di a ed i lungo un’orbita circolare è:

𝛽_!/! = arctan𝛥𝑖 𝜋 𝑟

𝛥𝑟 (39)

mentre combinando le Eq. 33 – 35 – 38 si ottiene β per cambiamenti di

a e RAAN:

𝛽_!/! = arctan𝛥𝛺 𝜋 𝑟 sin 𝑖

𝛥𝑟 (40)

In entrambe le Eq. 39 e 40 è stato sostituito Δa con Δr poichè si stanno trattando orbite circolari, per le quali essi coincidono. Inoltre, in entrambe r ed i sono i valori del raggio e dell’inclinazione dell’orbita iniziale, e le variazioni dei parametri orbitali sono le variazioni ottenibili su un’orbita. Quindi, il valore di β cambia di orbita in orbita.

(36)