157
6.
ANALISI DEI DATI
Terminata l’attività sperimentale, sono stati effettuati l’analisi dei dati rilevati ed il confronto tra questi ed i valori ottenuti attraverso l’applicazione delle formule teoriche presentate nel Cap. 3 e la soluzione delle simulazioni C.F.D. (Computational Fluid Dynamics).
6.1. Valutazione preliminare dei risultati delle misure
Una volta completata la campagna prove indicata dalle tabelle in Figg. (5.64) e (5.65) al Cap. 5, è stato possibile procedere ad una prima valutazione qualitativa degli andamenti di pressione rilevati e del fenomeno fisico.
Da tale analisi si è evinto che, coerentemente con le indicazioni generali date dal principio di Bernoulli, l’entità delle variazioni della pressione e della temperatura lungo un raggio del piattello aumenta al crescere della portata ed al diminuire dell’altezza del meato.
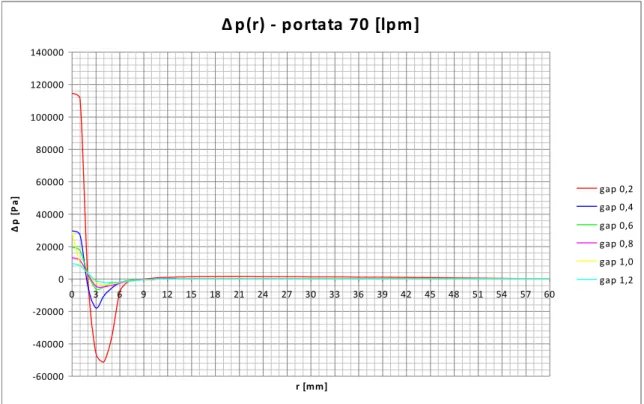
La Fig. 6.1. mostra l’andamento delle pressioni in funzione del raggio per tutti i gap impostati con una portata par a 70 lpm.
Δ p(r) - portata 70 *lpm+ -60000 -40000 -20000 0 20000 40000 60000 80000 100000 120000 140000 0 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 r [mm] Δ p [ P a ] gap 0,2 gap 0,4 gap 0,6 gap 0,8 gap 1,0 gap 1,2
Figura 6.1. Andamento delle pressioni relative per tutti i valori del gap impostati ad una portata di 70 lpm. Si può notare come i valori assoluti della pressione relativa crescano, a
parità di portata, al diminuire dell’altezza del meato.
E’ stato riscontrato anche che, per determinati valori del gap e della portata, la pressione relativa in zone relativamente ampie del piattello, distanti dall’asse, risulta positiva, con conseguente generazione di forza repulsiva fra le pareti del meato. Appropriata è risultata poi la scelta di infittire la frequenza dei rilievi sperimentali per i valori più bassi del raggio, inferiori a 12 mm, nella parte, quindi, più vicina all’asse del condotto verticale, date le variazioni molto marcate della pressione in questa zona del meato.
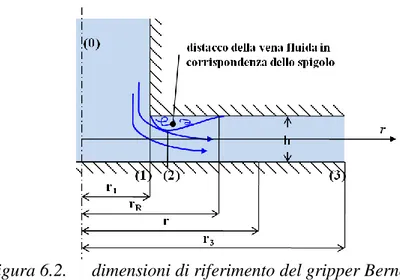
158 Figura 6.2. dimensioni di riferimento del gripper Bernoulli.
Come già accennato nel Cap. 5, (Par. 5.2.1.2), è stato verificato che la pressione assoluta per r=r3 di Fig. 6.2 coincide, praticamente, con quella atmosferica: ciò significa che, in tale sezione, gli effetti dell’efflusso radiale sono del tutto trascurabili.
L’analisi degli andamenti, al variare del gap e della portata, ha consentito di individuare alcune combinazioni di questi due parametri, per le quali risultasse proficuo confrontare i valori rilevati sperimentalmente con quelli forniti da modelli matematici e soluzioni C.F.D., riportate il Tab. 6.1. CONFIGURAZIONE GRIPPER Di = 4,0mm / Di = 8,6mm De = 120mm
*
* * *
* * * *
* * *
30 P O R TA TA [ lp m ]*
* * * * * * * * * * * * * * * *
50*
* * *
* * * *
* * * *
70*
*
* * * * * * * * * * * * * * *
90* *
* * * * * * * * * * * * *
110* * *
* * * *
* * * *
130 0 ,2 0 ,3 0 ,4 0 ,6 0 ,8 1 ,0 1 ,2 1 ,4 1 ,6 1 ,8 2 ,0 2 ,5 3 ,0 3 ,5 4 ,0 4 ,5 5 ,0 GAP [mm]Tabella 6.1. Matrice delle prove con indicazione delle combinazioni di gap e portata considerate per il confronto fra dati teorici e dati sperimentali. Tali combinazioni sono indicate dai simboli in grigio. Esse sono state investigate per entrambe le configurazioni del
gripper, tranne che quelle con h=0,3mm e quella con h=0,6mm e Q=130lpm. La combinazione h=0,6 e Q=110lpm è stata presa in considerazione solo per il gripper con
Di=8,6mm. Gli asterischi in rosso indicano prove effettuate solo con il gripper in configurazione con Di=8,6mm.
159 Come visibile in Tab. 6.1., sempre coprendo un’ampia gamma di condizioni pratiche applicative, si è scelto di investigare valori del gap di separazione relativamente bassi, in corrispondenza dei quali si verificano gli effetti più significativi. I valori dell’altezza del meato superiori a 3mm sono stati esclusi perché, per essi, gli effetti dell’efflusso radiale sono stati ritenuti poco rilevanti.
6.2. Adimensionalizzazione
I risultati verranno presentati in forma adimensionale, ponendo:
dove, con riferimento alla Fig. 6.2, Q è la portata [m3/s], ρ è la densità del fluido [Kg/m3], μ la viscosità dinamica [Pa·s], D1=2 r1 [m], patm è la pressione atmosferica [Pa], p(r) è la pressione assoluta [Pa] misurata o calcolata e u0 è la velocità del fluido in [m/s] in corrispondenza della sezione (0).
6.3. Stima dell’errore sulle misurazioni della pressione
Le misure effettuate sono naturalmente affette da errori. E’ stato possibile stimare numericamente alcuni di essi, cosiddetti casuali (random errors). Gli errori sistematici (bias errors), invece, quando non noti a priori, sono risultati ineliminabili e di impossibile quantificazione. In generale, gli errori sono stati determinati dalle differenze fra il modello di prova ideale e quello realmente impiegato negli esperimenti. Gli effetti di queste discrepanze si manifestano contemporaneamente e sono difficilmente separabili. Essi sono dovuti, fra l’altro, alla non costanza del gap, all’imprecisa regolazione della portata d’aria, agli errori di posizionamento sul piano (X-Y) e lungo l’asse Z del polso del robot S.C.A.R.A., all’errore di ortogonalità fra asse del condotto verticale della boccola e superficie attiva della piastra, alla forma dello spigolo tra lo stesso condotto ed il piattello.
Per poter effettuare un confronto efficace fra i valori di pressione e temperatura calcolati od estrapolati dalle soluzioni delle simulazioni C.F.D., e quelli rilevati sperimentalmente, si è reso necessario eseguire una stima, se pur grossolana, dell’incertezza dei valori misurati al fine di attribuirgli un intervallo di confidenza, ancorché di prima approssimazione.
6.3.1 Errore casuale
Per ciascuna delle combinazioni di (h, Q) scelte per il confronto dei dati (contraddistinte con il simbolo del grafico in Tab. 6.1), sono state effettuate cinque serie di rilievi della pressione, per un totale di 125 prove, secondo una sequenza operazionale analoga a quella indicata nel Cap.5, Par. 5.2.1.4, interrompendo però il flusso al termine di ogni serie di rilievi agendo ora sui flussometri e non più sulla valvola di intercettazione a monte di essi, lasciata in posizione aperta. La portata dunque è stata regolata ad ogni ripetizione. Ciò ha consentito, per ogni valore di pressione, di calcolare una media, ed attribuire ad essa una deviazione standard, secondo le tradizionali formule della statistica([2], [37]):
160 con n=5, numero di misure della pressione al raggio r.
6.3.2 Errore sistematico
Alcuni errori sistematici sono risultati noti e corrispondenti alle incertezze degli strumenti di misura utilizzati (i cui valori sono riportati al Par. 5.1.5 e Cap. 5). E’ stato possibile quindi considerare tali incertezze nel calcolo della deviazione standard da attribuire alla media dei dati sperimentali rilevati, secondo la
dove σS rappresenta l’incertezza dello strumento di misura.
Gli altri errori sistematici, causati da un insieme di diversi fattori, fra cui quelli elencati precedentemente e i cui singoli effetti non sono isolabili, sono risultati non essere quantificabili numericamente. Tuttavia, è stato possibile determinare approssimativamente i casi in cui i loro effetti potessero essere considerati trascurabili. Infatti, detti fattori determinano un andamento della pressione non simmetrico, lungo un diametro, rispetto all’asse del condotto verticale (r=0), ovvero p(r) ≠ p(-r) (Fig. 6.3). L’andamento di pressione in condizioni ideali è, invece, simmetrico, ovvero si ha che p(r) = p(-r). E’ stato possibile definire allora una grandezza, la asimmetria A(r), che tiene conto degli scostamenti dell’andamento reale rispetto a quello ideale:
A(r) = p(r) - p(-r)
Figura 6.3. Andamento della pressione sul diametro per gripper con Di=8mm, Q=30lpm, gap 0,2mm(blu), 0,6mm(verde), 2,0mm(rosso) e angolo di inclinazione del piattello α=0°,0’,30’’ corrispondente ad un errore di parallelismo sul diametro di circa 0,1mm, cautelativamente superiore a quelli effettivamente riscontrati durante la campagna prove.
161 Figura 6.4. Andamento del valor medio delle pressioni misurate p(r) e p(-r) (in rosso) ed il
valore assoluto della discrepanza A(r) fra questo ed il valore misurato(in blu).
Dall’analisi della Fig. 6.3 si nota come i fattori che determinano l’andamento asimmetrico della pressione abbiano un’incidenza direttamente proporzionale alla portata ed inversamente proporzionale all’altezza del meato. A(r), infatti, come visibile dai grafici di Figg. 6.3 e 6.4, diminuisce all’aumentare del gap, fino a diventare praticamente nulla per valori di h sufficientemente grandi, dell’ordine di 0,4mm. In questi casi, l’andamento della pressione diviene quindi quasi perfettamente simmetrico ed è sembrato ragionevole considerare gli errori sistematici trascurabili.
Non significativi, infine, sono risultati gli errori introdotti dalla imprecisione di posizionamento, sia sul piano (X-Y) che lungo l’asse Z del polso del robot, come si evince anche dell’estrema ripetibilità delle prove (si veda Cap. 5, Par. 5.2.2).
In conclusione, nei casi in cui gli errori sistematici incogniti possono essere considerati trascurabili, la stima, in prima approssimazione, dell’incertezza dei valori misurati può essere assunta pari a quella fornita dalla (6.4). A titolo d’esempio si riportano, in Fig. 6.5, gli intervalli di incertezza attribuiti al valor medio delle pressioni misurate per h*=0,05, Q=30lpm e D3/D1=30. Si noti come le incertezze crescano al tendere del raggio a zero. Ciò è
dovuto in parte all’impiego di strumenti di misurazione della pressione caratterizzati da σS maggiore ed in parte alla più marcata influenza che gli errori commessi nella regolazione della portata hanno in questa zona del piattello, nella quale piccole variazioni di Q determinano, data la conservazione della portata, grandi variazioni di velocità del fluido e quindi della sua pressione.
E’ stato altresì verificato che l’incertezza relativa, σREL(r) data dalla
162 Figura 6.5. Valori medi con relativi intervalli di confidenza.
Per esigenze cautelative e di praticità, è apparso dunque ragionevole attribuire a tutti i valori di pressione misurati uno stesso valore di incertezza, pari a quello massimo riscontrato caso per caso.
6.4
Criterio di accettazione dei dati
E’ stato deciso cautelativamente di considerare poco attendibili le misure per cui risultasse |A(r)|max > | σS |max
con σS incertezza dello strumento di misura. Per tutti gli altri casi si assume A(r) ≈ 0 e gli errori sistematici, eccetto l’incertezza degli strumenti di misura, vengono considerati trascurabili.
Vengono considerati non accettabili i valori di pressione, calcolati tramite i modelli teorici o estrapolati dalle simulazioni realizzate in Fluent®, che cadono fuori dall’intervallo di confidenza ± .
6.5
Validazione delle simulazioni CFD e loro valutazione
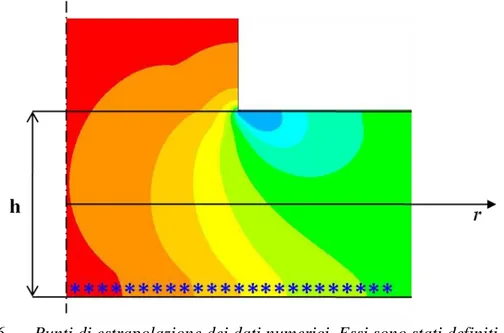
Per effettuare un confronto con le distribuzioni di pressione ottenute sperimentalmente, l’andamento delle stesse ottenuto dalle soluzioni dei modelli ai volumi finiti è stato estrapolato su una linea prossima alla parete inferiore del condotto, ad una distanza tale da consentire di valutare la pressione all’interno del flusso ma non oltre l’altezza del sottostrato laminare.
163 Figura 6.6 Punti di estrapolazione dei dati numerici. Essi sono stati definiti lungo una
linea nel flusso all’interno del sottostrato laminare.
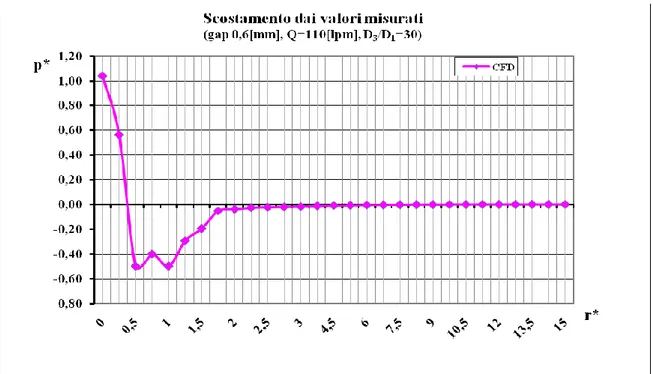
Le discrepanze maggiori si presentano nei valori della pressione di ristagno, come visibile in Fig. 6.8, e sono dovute essenzialmente alle approssimazioni introdotte nel modello, in particolare per quanto riguarda la temperatura d’ingresso (vedi Cap. 4). In ogni caso, comunque, i risultati estrapolati cadono all’interno dell’intervallo di accettazione precedentemente definito e risultano dunque utilizzabili per studiare qualitativamente i fenomeni che avvengono all’interno del meato.
Figura 6.7. Andamento delle pressioni relative misurate (in rosso) e dei valori estrapolati dalle soluzioni delle simulazioni del modello ai volumi finiti (in giallo), per h* = 0,15, Q* =
10456 e D3/D1 = 30. Si evince come l’utilizzo del software Fluent® permetta di stimare l’andamento della pressione anche al di fuori del meato.
164 Figura 6.8 Andamento lungo il raggio degli scostamenti dei valori estrapolati dalla
soluzione del modello ai volumi finiti rispetto ai valori misurati.
Dalla visualizzazione dell’andamento della velocità (Fig. 6.9(a)), si evince che, in corrispondenza dello spigolo fra condotto verticale e piattello (modellato come uno spigolo vivo), si verifica sempre il distacco del flusso d’aria, con conseguente insorgenza della vena contracta . In tale zona si verificano spesso le condizioni per l’insorgere di moto turbolento e la velocità del fluido mostra un’inversione in prossimità del piattello. Tale inversione è ben visualizzabile dal grafico di Fig. 6.9(b), dove il profilo di velocità diventa negativo in prossimità del piattello.
Figura 6.9 (a)Visualizzazione globale dell’andamento della velocità. Si notano il ristagno in corrispondenza della zona di impatto del getto d’aria con la parete del piattello(in blu), l’accelerazione del fluido in corrispondenza dello spigolo ed il conseguente distacco della
vena. (b) Andamento del profilo della velocità in corrispondenza di una sezione effettuata nella zona di distacco del flusso. Si può osservare l’inversione in prossimità del piattello (x =
165 Superata la zona dove di distacco della vena fluida, il moto risulta laminare pienamente sviluppato per ogni caso studiato.
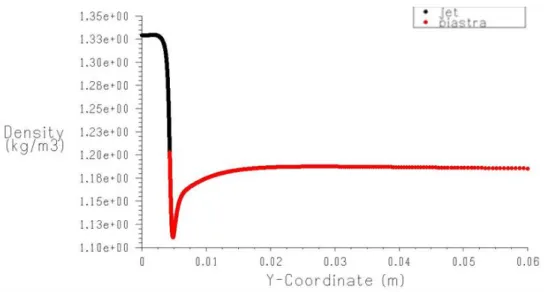
I valori ottenuti per i numeri di Mach e Reynolds lungo il meato forniscono una precisa indicazione riguardo il regime di moto e lo stato del fluido. Esso risulta sempre, eccetto per la vena contracta, praticamente incomprimibile. Una conferma di ciò è fornita dall’andamento della densità lungo il raggio, riportato in Fig. 6.10. Si nota come, in prossimità dell’asse del gripper , il fluido abbia un elevata densità per effetto dell’impatto contro la parete del gripper(porzione della curva in nero). Successivamente, dopo un picco di abbassamento dovuto all’espansione, torna su valori praticamente costanti, confermando la bontà del modello incomprimibile per lo studio della zona oltre la vena contracta.
Figura 6.10 Variazione della densità lungo il meato. In nero è rappresentato l’andamento per r < r1 (jet), mentre in rosso quello per r1 < r <r3 (piastra).
Per quanto riguarda, invece, il moto del fluido, l’analisi dei numeri di Reynolds locali ha confermato la possibilità dell’insorgere di fenomeni locali di turbolenza, soprattutto all’aumentare del gap e della portata. Tali fenomeni, confermando l’analisi effettuata, si verificano sempre in corrispondenza della strizione generata dalla vena contracta, come evidente dall’andamento riportato in Fig. 6.11.
Figura 6.11 Visualizzazione del numero di Reynolds Re che evidenzia l’insorgere di fenomeni di turbolenza locale (in rosso)in corrispondenza della zona di vena contracta.
166 Le simulazioni consentono inoltre, a differenza delle formule sperimentali che sono applicabili soltanto all’efflusso radiale, di stimare l’andamento della pressione anche per r < r1.
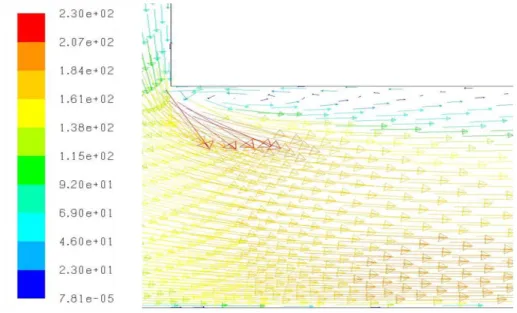
Un importante risultato ottenuto grazie ai dati estrapolati dalle soluzioni dei modelli ai volumi finiti è stata la stima del reattachment radius, rR per tutti i casi studiati. Per eseguire tale stima sono stati considerati gli angoli che i vettori velocità formano, localmente, con l’asse del condotto verticale: l’andamento tipico di tali vettori nella porzione di meato soggetta a distacco della vena fluida è riportato in Fig. 6.12.
Figura 6.12 Visualizzazione dei vettori velocità nella zona di meato interessata dal fenomeno della vena contracta.
rR è stato posto pari al valore del raggio in corrispondenza del qual tale angolo è risultato essere pari a 90°, ovvero termina in distacco della vena fluida. Gli andamenti in funzione di Q* sono riportati in Fig. 6.13. I valori trovati mostrano buon accordo con quelli presentati da Moller (Cap.2, [20] e [21]). Per portate (e quindi valori di Re) sufficientemente elevati, rR risulta funzione, praticamente, soltanto di h*.
167 Figura 6.13 Stima della variazione del reattachment radius rR, in funzione di Q*, al variare
di h* per D3/D1=30 e D3/D1=15 .
6.6
Confronto fra dati sperimentali e formule teoriche
L’analisi qualitativa del fenomeno e la valutazione quantitativa dei vari parametri che lo definiscono, effettuate tramite i dati ottenuti dalle simulazioni e quelli calcolati in base ai rilievi sperimentali (Ma, Re e velocità) per le combinazioni di h e Q riportate in Tab. 6.1, hanno permesso di definire il tipo di flusso per ogni prova effettuata. Esso è risultato essere, eccezion fatta per la zona della vena contracta, laminare, ed è stato possibile considerare il fluido incomprimibile, ricadendo quindi sempre nel quadrante I del grafico di Fig.6.13 che viene qui riproposto.
168 Figura 6.14 Grafico Ma-Re, il quale definisce le quattro zone che caratterizzano ogni possibile stato del fluido in moto in un condotto. Le formule proposte, indicate dai propri numeri di riferimento(in rosso), vengono inserite all’interno dei rispettivi campi di validità.
La zona evidenziata in verde rappresenta il campo in cui si trovano le prove effettuate.
La formula (2.4) è stata esclusa a priori dal confronto poiché, essendo di natura sperimentale, dipende fortemente da coefficienti empirici validi solo per il particolare gripper utilizzato, diverso, per configurazione e geometria, da quelli impiegati per la presente attività sperimentale.
Il confronto si è ridotto quindi alle due formulazioni realizzate da Roura (3.2) e (3.42) con perdite calcolate secondo la (3.46) presentata in questo lavoro, di seguito riproposte per chiarezza espositiva:
Nella porzione del meato dove si ha efflusso laminare pienamente sviluppato, sia la (6.5) che la (6.6) rientrano negli intervalli d’incertezza dell’andamento di pressione, come visibile dagli andamenti riportati in Figg. 6.15 e 6.16. Nella zona interessata da distacco della vena fluida, invece, le ipotesi di flusso pienamente sviluppato i di fluido incomprimibile non sono più valide e queste formulazioni cadono in difetto dal punto di vista teorico e presentano discrepanze superiori alla confidenza delle misure, con conseguente inattendibilità dei dati forniti.
Sulla base anche delle indicazioni fornite dalle soluzioni in Fluent, si è quindi provato ad abbandonare, per r < rR, almeno l’ipotesi di incomprimibilità e ad utilizzare, per descrivere l’andamento reale del fluido, la formulazione della politropica data dalla (3.17) con n = 1,36. Per la stima delle perdite, è stata sfruttata la formulazione (3.32), integrata numericamente. Purtroppo, i risultati così ottenuti, come del resto prevedibile, non hanno portato miglioramenti nella stima dell’andamento della pressione nella zona di vena contracta:
169 l’errore rispetto ai dati sperimentali è risultato tale da non consentire di poter accettare questo modello come valido.
E’ sembrato dunque ragionevole ritornare alle formulazioni (6.5) e (6.6) che, pur mostrandosi anch’esse inadeguate, possiedono quantomeno la caratteristica di semplicità.
Figura 6.15 Andamento delle pressioni misurate(in rosso) e delle pressioni calcolate lungo il piattello del gripper secondo Roura (formula (6.5), in verde) e secondo la teoria presentata
in questo lavoro((6.6), in blu).
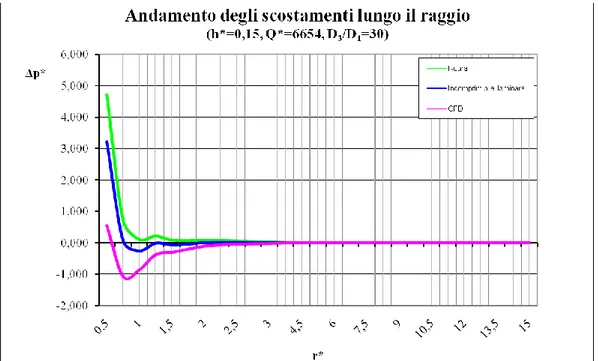
Figura 6.16 Scostamento, rispetto alle pressioni misurate, delle pressioni calcolate lungo il piattello del gripper secondo Roura (formula (6.5), in verde), secondo la teoria presentata in
170 Sempre la maggior facilità di utilizzo e la necessità di ricorrere ad un numero inferiore di coefficienti sperimentali, oltre ad un migliore accordo con gli andamenti medi di pressione rilevati, hanno portato ad individuare nella (6.6) la migliore stima dell’andamento reale di pressione. Si osservi, a tal riguardo, gli andamenti delle discrepanze in Fig. 6.16.
Si è scelto di riportare, a titolo di esempio, solo il confronto effettuato per h*=0,15, Q*=6654 e D3/D1=30. Per gli analoghi confronti, con le altre combinazioni di h* e Q* considerate, i dati sono riportati in Allegato IV.
Si deve notare come, data anche l’entità delle depressioni generate, la trattazione analitica che si basa sulle ipotesi di laminarità del flusso ed incomprimibilità del fluido per l’intero piattello, non tenendo conto dell’effetto di distacco della vena fluida(in pratica, le formule (6.5) e (6.6)), consente di descrivere, anche se solo in prima approssimazione, l’andamento di pressione con una precisione sufficiente per molti scopi pratici, come, ad esempio, una stima di prima approssimazione della forza di attrazione sviluppata FS.
6.7 Misure di temperatura
Poiché, per tutte le prove analizzate, il fluido è risultato incomprimibile in moto laminare, per studiarne il comportamento non è stato necessario considerarne la temperatura al variare del raggio. Non si è proceduto dunque ad una analisi accurata dei dati rilevati.
Un breve confronto, puramente qualitativo, fra gli andamenti misurati e quelli forniti dalle soluzioni dei modelli C.F.D., suggeriscono comunque che i valori rilevati sperimentalmente siano affetti da disturbi significativi e non eliminabili con l’attrezzatura e lo strumento di misura utilizzati.
6.8 Coefficiente correttivo K(r)
La formula (6.6) può essere considerata pienamente valida per valori del raggio superiori ad rR. Nella rimanente zona del piattello, come detto, essa si discosta invece dall’andamento reale. D’altra parte, l’analisi fin qui condotta ha confermato l’impossibilità di definire modelli, sia fisici che matematici, di validità generale (indipendenti quindi dalla geometria del gripper e dalle condizioni di esercizio), che riescano a descrivere bene il fenomeno.
E’ possibile però fornire per i casi analizzati, che comunque coprono un ampio range di condizioni di pratico interesse, una formulazione matematica che permetta di stimare con buona precisione l’andamento della pressione anche nella zona di vena contracta.
A tal fine, è stato definito il coefficiente correttivo K(r) come:
dove patm è la pressione atmosferica rilevata per ogni serie di misurazioni e p(r)sperim e p(r)teorica sono, rispettivamente, le pressioni relative misurata e calcolata tramite la (6.6). Tale coefficiente tiene implicitamente conto di parametri geometrici quali il raggio di raccordo fra condotto verticale e piattello e l’altezza del meato, e delle caratteristiche del flusso quali la portata, l’effetto del distacco della vena fluida e le locali condizioni di turbolenza e comprimibilità.
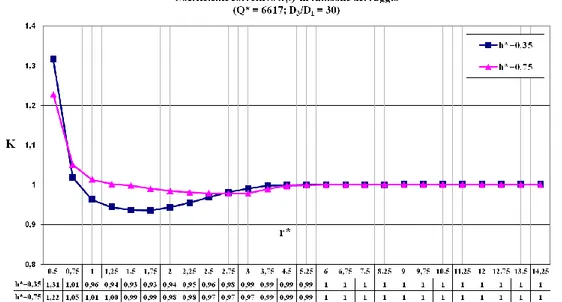
171 A titolo esemplificativo si riporta, in Fig. 6.17, l’andamento di K(r) per Q*= 6617 e D3/D1=30, al variare di h* tra alcuni valori discreti.
Figura 6.17. Andamento del fattore correttivo K, in funzione del raggio, al variare di h*. Per valori di r superiori a rR, K(r) può essere ragionevolmente considerato pari a 1.
Nella (6.7), l’utilizzo delle pressioni assolute consente di avere una definizione robusta dal punto di vista termodinamico del coefficiente, escludendo praticamente la possibilità che esso possa assumere forme indeterminate. Il suo domino fisico di esistenza risulta essere infatti dato dall’intervallo [0; +∞[ .
Per come è stato definito, esso fornisce una stima dello scostamento del modello teorico dalle condizioni reali. In particolare, tale parametro indica una sovrastima dell’andamento reale della pressione per valori di K(r) < 1 e una sottostima per K(r) >1. Come si vede dai dati tabulati sotto il grafico di Fig. 6.14, per valori di r > rR, risulta sempre essere K(r) ≈ 1, a conferma della bontà del modello teorico in questa zona del piattello.
K(r) così valutato risulta essere discreto, definito cioè solo per i valori del raggio in corrispondenza dei quali vengono effettuate le misure.
Volendo ottenere invece, per esso, una funzione continua in grado di fornire la correzione da apportare a p(r)teorica per valori di r compresi nell’intervallo [Di/2; rR], è stato possibile, attraverso l’utilizzo del software Mathcad®
, calcolare la curva interpolante i valori di K(r), di equazione
Si è deciso di porre m=4 perché rappresenta, per i casi analizzati, un buon compromesso tra accuratezza della stima di K(r) e praticità d’uso. In Fig. 6.18 si riporta la curva di interpolazione di K(r) per D3/D1= 30, Q*=6617, h*=0,35.
In sintesi, dunque, l’andamento della pressione per i casi presi in esame può essere stimato tramite la
172 Figura 6.18 Curva di interpolazione per D3/D1= 30, Q=130lpm, h*=0,35, avente costanti a0 = 2,263; a1 = -0,715; a2 = 0,135; a3 = -0,011; a4 = 3,055·10-4.La deviazione
standard dei residui è σRES=0,027.
I valori dei coefficienti del polinomio interpolante (6.8) per tutti i casi analizzati sono riportati dei seguito nelle Tabb. 6.2 e 6.3.
E’ evidente che i valori dei coefficienti K(r) dipendono dalla particolare configurazione del gripper considerata, come del resto l’altezza e l’estensione della zona di vena contracta. Allo stato attuale, d’altra parte, non è possibile ottenere un’espressione di validità generale.
D3/D1 = 30 h* a0 a1 a2 a3 a4 rR/D1 σres Q* = 2851 0,05# 2,24 -0,737 0,149 -0,013 3,731·10-4 0,75 0,039 0,15 1,213 -0,129 0,026 -2,064·10-3 5,82·10-5 1,25 6,516·10-3 0,35 1,062 -0,033 5,79·10 -3 -4,222·10 -4 1,099·10 -5 2,75 6,431·10 -4 0,75 1,034 -0,016 2,731·10 -3 -1,946·10 -4 5,028·10 -6 5 4,849·10 -4 Q* = 6653 0,05# -18,402 10,703 -2,038 0,161 -4,486·10 -3 1,5 0,781 0,15 1,779 -0,441 0,085 -6,669·10-3 1,857·10 -4 1,5 0,024 0,35 1,241 -0,13 0,023 -1,691·10 -3 4,434·10 -5 3,25 4,122·10 -3 0,75 1,142 -0,073 0,013 -1,011·10 -3 2,804·10 -5 6,5 2,59·10 -3 Q* = 10456 0,15 4,001 -1,815 0,357 -0,028 7,946·10 -4 1,75 0,109 Q* = 12357 0,35 2,159 -0,629 0,112 -8,315·10-3 2,212·10-4 3,5 0,028 0,75 1,743 -0,387 0,071 -5,538·10-3 1,551·10-4 7,5 0,017
Tabella 6.2 La tabella raccoglie i coefficienti di ( )
~
r
K per il gripper con D
3/D1 = 30 (Di = 4 mm), per r < rR. Per r > rR si pone K(r) = 1. I valori del gap contrassegnati da (#) non sono ritenuti completamente attendibili, ma vengono ugualmente riportati i relativi coefficienti, utili per un grossolano calcolo di prima approssimazione. La σres è data dall’espressione:
5 ) ( ~ ) ( 1 2 1 n r K r K n i i res ,
173 D3/D1 = 15 h* a0 a1 a2 a3 a4 rR/D1 σres Q* = 1426 0,05# 1.014 -6.472·10-3 1.047·10-3 -7.252·10-5 1.833·10-6 0,625 1.48·10-4 0,075 1.002 -8.555·10-4 1.356·10-4 -9.113·10-6 2.216·10-7 0,75 2.119·10-5 0,175 1 -1.411·10-4 1.899·10-5 -1.049·10-6 2.024·10-8 1,375 3.817·10-6 0,375 1 -2.391·10-5 2.295·10-6 -9.098·10-8 1.362·10-9 2,625 7.733·10-7 Q* = 3326 0,05# 1.015 -6.98·10-3 1.148·10-3 -8.069·10-5 2.055·10-6 0,625 1.698·10-4 0,075 1.002 -8.73·10-4 1.428·10-4 -9.945·10-6 2.506·10-7 0,875 2.002·10-5 0,175 1 -1.362·10-4 1.845·10-5 -1.04·10-6 2.086·10-8 1,625 3.262·10-6 0,375 1 -2.416·10-5 2.579·10-6 -1.246·10-7 2.453·10-9 3,125 6.712·10-7 Q* = 6178 0,075 1.002 -9.511·10-4 1.553·10-4 -1.074·10-5 2.683·10-7 0,875 3.008·10-5 0,175 1 -1.349·10-4 1.613·10-5 -7.409·10-7 1.03·10-8 1,75 4.812·10-6 0,375 1 -2.131·10-5 1.493·10-6 -1.778·10-8 -8.05·10-10 3,875 9.457·10-7
Tabella 6.3 La tabella raccoglie i coefficienti di ( )
~
r
K per il gripper con D
3/D1 = 15 (Di = 8 mm), per r < rR. Per r > rR si pone K(r) = 1. I valori del gap contrassegnati da (#) non sono ritenuti completamente attendibili, ma vengono ugualmente riportati i relativi coefficienti, utili per un grossolano calcolo di prima approssimazione. La σres è data dall’espressione:
5 ) ( ~ ) ( 1 2 1 n r K r K n i i res ,
con n = numero dei valori del raggio considerati per la determinazione dei K(r).
6.9 Possibili ottimizzazioni geometriche
Dall’analisi qui compiuta, come dagli studi eseguiti riguardanti il gripper Bernoulli, appare chiaro che il suo funzionamento e, di conseguenza, le sue prestazioni, sono governati dal comportamento del fluido nella zona della vena contracta. E’ dunque ovvio che ogni tentativo di ottimizzazione geometrica debba muovere dal tentativo di controllare il flusso in tale porzione del meato e di massimizzarne gli effetti positivi sulla depressione.
In quest’ottica, i dati reperiti in letteratura, l’analisi del fenomeno sopra esposta e, soprattutto, le indicazione fornite dalle soluzioni dei modelli ai volumi finiti, forniscono alcuni spunti per proporre, a titolo puramente indicativo e qualitativo, possibili configurazioni geometriche ottimizzate del gripper, onde rendere più performante l’effetto di presa.
L’esame del flusso suggerisce che, nella zona di distacco della vena fluida, una significativa porzione del volume del meato è occupata, nella parte superiore, da aria ferma. E’ intuitivo, quindi, pensare di “riempire” tale settore, conformando il piattello superiore del gripper secondo una linea suggerita dall’andamento della stessa vena contracta, come mostrato in Fig. 6.19.
174 Figura 6.19 Andamento ipotetico di un profilo del piattello del gripper Bernoulli ottimizzato
in funzione delle linee di flusso. Si noti in particolare la forma del profilo della generatrice del deflettore, che risulta assimilabile a quello tipico delle valvole dei motori a combustione interna.
La forma del meato è stata ottimizzata basandosi sulle indicazioni fornite dalle simulazioni effettuate in Fluent® che, come già affermato in precedente, si è dimostrato un valido ed attendibile strumento di analisi previsionale.
L’utilizzo del deflettore, in una simile conformazione geometrica, aiuta a convogliare il flusso d’aria verso la sezione di gola, evitando eccessive perdite di carico, brusche variazioni di direzione e, naturalmente, riduce la forza repulsiva Fjet. La geometria proposta dovrebbe consentire un controllo ed una descrizione precisi del flusso stesso e di minimizzare gli effetti indesiderati conservando al tempo stesso la strizione della sezione di passaggio che è all’origine della forte caduta di pressione. Essa comunque, poiché il fenomeno è strettamente dipendente dalla portata e dall’altezza del gap di separazione, sarà efficiente, con tutta probabilità, solo per alcune combinazioni dei due suddetti parametri.
Naturalmente, un’altra possibilità di ridurre gli effetti indesiderati della vena contracta e, al contempo, massimizzare gli effetti positivi della strizione, è data dall’utilizzo di un deflettore appositamente conformato (Fig. 6.20). Il profilo di tale deflettore, all’incirca parabolico, unitamente all’ampio raggio di raccordo dello spigolo tra condotto di asservimento dell’aria e piattello del gripper, consente di deviare il flusso in maniera graduale. La sezione di passaggio dovrebbe poter essere regolata a seconda delle esigenze.
Figura 6.20. Soluzione di Bernoulli gripper con deflettore a fungo (fonte [6]). Comunque, potrebbero essere significativi i vantaggi derivanti dal conformare la parte terminale del piattello in modo da rendere più accentuato, al variare del raggio, l’aumento di sezione di passaggio.
![Figura 6.20. Soluzione di Bernoulli gripper con deflettore a fungo (fonte [6]).](https://thumb-eu.123doks.com/thumbv2/123dokorg/7532217.107180/18.892.120.777.105.333/figura-soluzione-bernoulli-gripper-deflettore-fungo-fonte.webp)