Capitolo 6 Risultati numerici e conclusioni

Capitolo 6

Risultati numerici e conclusioni

Abbiamo utilizzato i programmi da noi sviluppati per calcolare auto-stati Hartree-Fock di un sistema di elettroni confinato in una scatola cubi-ca: da questi abbiamo ricavato energia dello stato fondamentale ed ener-gia HOMO-LUMO e profilo della densità elettronica ρ. Abbiamo eseguito i calcoli al variare del numero di elettroni, fissando la densità elettronica desiderata: il volume della scatola è in tal modo univocamente determina-to dalla relazione ρ = N/V. Parte dei calcoli è stata effettuata a densità 1, principalmente per confronto con calcoli simili [36], un’altra parte usando la densità elettronica di un bulk d’oro: considerando che il parametro rs per questo metallo è 3.01 [16], abbiamo ρ = 8.754108 · 10−3

A partire dai risultati Hartree-Fock abbiamo calcolato la polarizzabilità statica con metodi TDHF e MP2. Abbiamo utilizzato il metodo MP2 sola-mente come confronto per il metodo TDHF, in quanto l’introduzione di un campo elettrico nell’Hamiltoniano rompe la simmetria del problema: gran parte delle ottimizzazioni da noi sviluppate perdono efficacia su di un sistema di simmetria più ridotta e a questo si somma il dover effettuare svariate iterazioni per avere dati a disposizione per intensità diverse del campo.

Nell’ultima parte abbiamo poi ricalcolato le quantità di interesse con l’aggiunta di un volume di spill out per valutare la correzione apporta-ta; abbiamo valutato poi l’andamento della polarizzabilità al variare del volume dello spill out per testare la validità e i limiti del modello.

6.1 LIVELLI ENERGETICI E PROFILI DI DENSITÀ 51

6.1

Livelli energetici e profili di densità

In una simulazione come la nostra, basata su una scatola cubica, i livelli energetici non sono in linea di principio gli stessi ricavabili per un model-lo a simmetria sferica, con il quale si ottengono autofunzioni diverse, sia per tipo che per numero. Nonostante questo i numeri magici rimangono gli stessi in entrambi i modelli e coincidono con quelli osservati sperimen-talmente: riportiamo, come indicato da De Heer [6], le dimensioni dei clu-ster per i quali si osserva particolare stabilità. Inoltre è spesso riscontrato [40] che le energie ed i comportamenti generali di un jellium valutati con una scatola cubica o con una sfera differiscono per un fattore geometrico dell’ordine dell’unità.

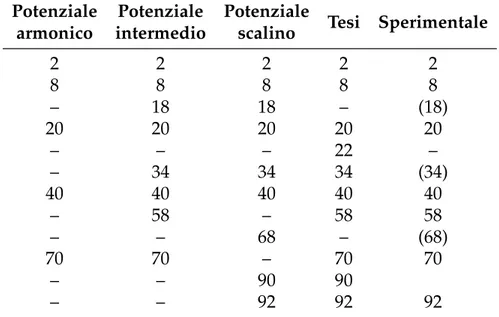
Potenziale Potenziale Potenziale

Tesi Sperimentale armonico intermedio scalino

2 2 2 2 2 8 8 8 8 8 – 18 18 – (18) 20 20 20 20 20 – – – 22 – – 34 34 34 (34) 40 40 40 40 40 – 58 – 58 58 – – 68 – (68) 70 70 – 70 70 – – 90 90 – – 92 92 92

Tabella 6.1:Numeri magici di cluster con vari modelli: il primo è un cluster

sferico con potenziale armonico, il secondo con un potenziale intermedio ar-monico/buca, il terzo con un potenziale a buca; il quarto è il nostro modello di cluster cubico, l’ultimo numeri magici di cluster di Sodio (sono indicati tra parentesi i picchi di abbondanza secondari). Dati tratti da De Heer [6].

La densità elettronica calcolata è simile a quella riscontrata per calco-li analoghi effettuati per cluster sferici riportata nel secondo capitolo ma, mentre per questi ultimi la densità radiale illustra efficacemente la distri-buzione di carica, nel nostro caso per chiarezza abbiamo graficato diver-se diver-sezioni del cubo. Abbiamo inoltre normalizzato a π le dimensioni dei cluster per facilitare il confronto tra cluster di dimesioni diverse;

l’inte-6.1 LIVELLI ENERGETICI E PROFILI DI DENSITÀ 52

grale della densità di carica elettronica su tutto il volume del cubo è per definizione pari al numero di elettroni.

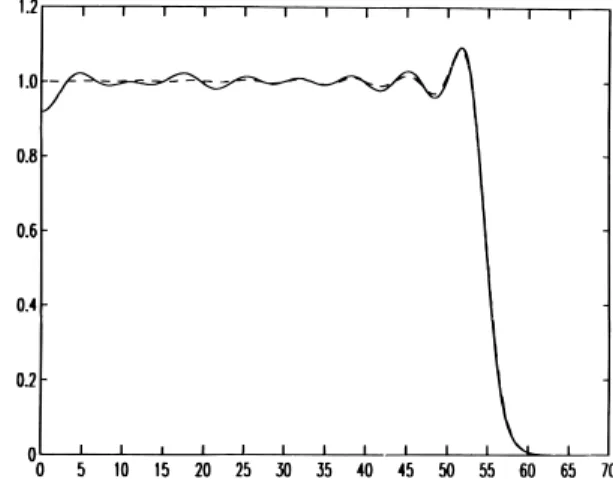
Possiamo osservare come per i cluster più piccoli la densità abbia un solo picco al centro del cubo, come si vede in figura 6.2; per cluster più grandi sono presenti altri massimi oltre a quello centrale, mentre la den-sità elettronica si sposta all’esterno, con picchi situati simmetricamente sulle quattro diagonali del cubo: questo comportamento si accentua al-l’aumentare del numero di elettroni. Uno spostamento progressivo della carica elettronica verso l’esterno è comunque confermato in letteratura, ad esempio da Serra [41], ma ci aspettiamo che al limite, per cluster più gran-di gran-di quelli trattati qui, il profilo gran-di densità tenda a gran-diventare quella gran-di una distribuzione di Fermi standard, come indicato da Genzken e Brack [42].

Figura 6.1:Comportamento asintotico della densità elettronica (in unità

del-la densità del jellium): in linea continua il profilo di densità per un cluster sferico di sodio con 2654 atomi [42]; in linea tratteggiata la densità elettronica perpendicolare alla superficie di un bulk di sodio semi infinito [18]. Immagine tratta da Brack [24].

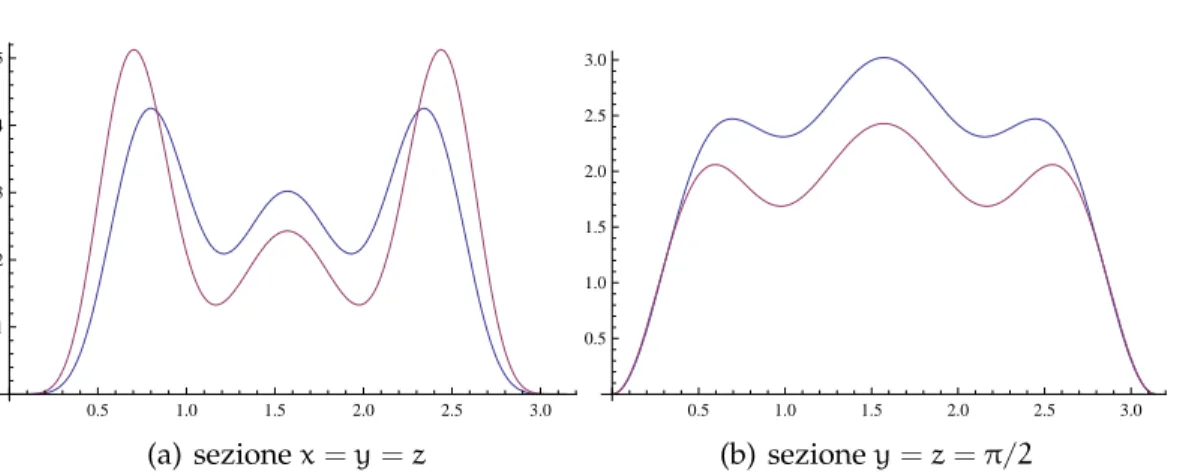
Per cluster di densità diversa da 1 si osserva lo stesso comportamento: i profili nei due casi sono molto simili, quando normalizzati sulle stesse dimensioni e si osserva lo stesso andamento all’aumentare del numero di elettroni. Per la densità pari a 0.00875 si osserva una maggiore definizio-ne dei picchi. Riportiamo come esempio il caso a 22 elettroni in figura 6.3: nella prima figura è evidenziato come lungo una diagonale del cubo i pic-chi siano più evidenti, mentre in una sezione parallela ad uno spigolo è presente meno carica.

I casi fin qui trattati mostrano un profilo di densità simile a quello in cui alla carica viene permesso di fuoriuscire dalla barriera del jellium:

ab-6.1 LIVELLI ENERGETICI E PROFILI DI DENSITÀ 53 0 1 2 3 0 1 2 3 0.0 0.2 0.4 0.6 0.8

(a) 2 elettroni, sezione z = y

0.5 1.0 1.5 2.0 2.5 3.0 0.2 0.4 0.6 0.8 (b) 2 elettroni, sezione z = y = π/2 0 1 2 3 0 1 2 3 0 2 4 (c) 20 elettroni, sezione z = y 0.5 1.0 1.5 2.0 2.5 3.0 0.5 1.0 1.5 2.0 (d) 20 elettroni, sezione z = y = π/2 0 1 2 3 0 1 2 3 0 5 10 15 20

(e) 108 elettroni, sezione z = y

0.5 1.0 1.5 2.0 2.5 3.0 2 4 6 8 (f) 108 elettroni, sezione z = y = π/2

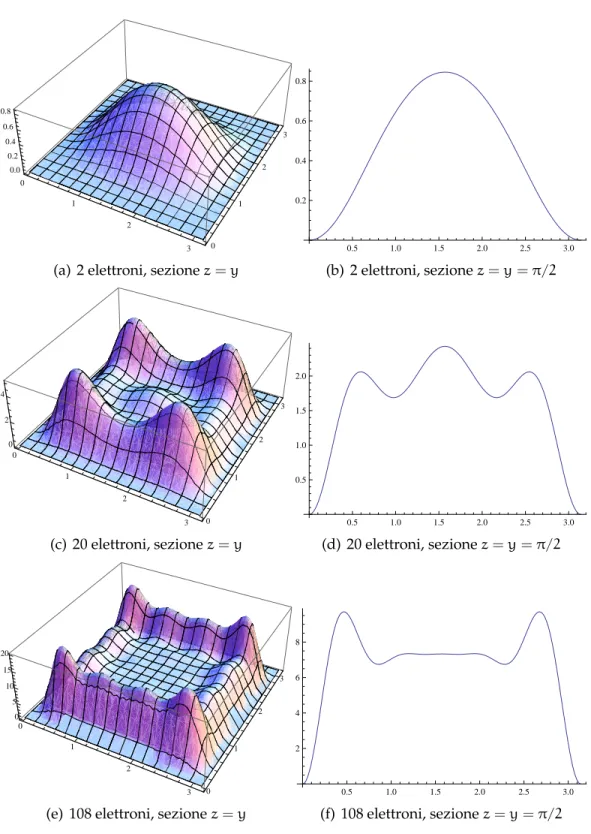
Figura 6.2:Rappresentazione grafica tridimensionale della densità elettronica

1 ρ = 1 a numero di elettroni variabile: per chiarezza abbiamo indicato anche l’andamento della densità in una sezione parallela allo spigolo

6.2 CALCOLO DELLE ENERGIE IN ASSENZA DI SPILL OUT 54 0.5 1.0 1.5 2.0 2.5 3.0 1 2 3 4 5 (a) sezione x = y = z 0.5 1.0 1.5 2.0 2.5 3.0 0.5 1.0 1.5 2.0 2.5 3.0 (b) sezione y = z = π/2

Figura 6.3:Rappresentazione grafica della densità elettronica per un cluster

di 22 elettroni: in azzurro per ρ = 1 e in viola per ρ = 0.00875

biamo considerato, per un cluster d’oro, un valore di spill out stimato a 1.4ua come suggerito da letteratura. La densità di carica è più concentra-ta all’interno del jellium, dove è controbilanciaconcentra-ta dalla carica positiva; nei casi con più elettroni notiamo come i picchi sugli spigoli appaiono legge-mente più marcati, mentre si assiste ad una uniformizzazione sul resto del volume.

Non è possibile calcolare il parametro q introdotto nell’espressione 1.2 e definito per cluster sferici, ma è possibile ricavare la carica elettronica presente nel volume aggiuntivo: seguendo la notazione del paragrafo 5.3 possiamo scrivere la carica desiderata come differenza tra quella totale e quella interna al volume del jellium:

ZZZwπ 0 dxdydzρ(r) − ZZZwπ−η η dxdydzρ(r) = N − ZZZwπ−η η dxdydzρ(r) I calcoli da noi effettuati mostrano come la carica esterna al jellium nel caso in cui l’effetto dello spill out è maggiore, un cubo contenente solo 2 elettroni, sia pari al 12.10% della carica totale; questo valore diminuisce al 6.94% per un un cluster di 22 elettroni e al 5.67% per un cluster di 88 elettroni.

6.2

Calcolo delle energie in assenza di spill out

In assenza di spill out il modello da noi sviluppato è quasi identico a quello elaborato in un articolo di Ghosh e Gill [36]: l’unica differenza

6.2 CALCOLO DELLE ENERGIE IN ASSENZA DI SPILL OUT 55 0.5 1.0 1.5 2.0 2.5 3.0 0.05 0.10 0.15 0.20 0.25 0.30

(a) 2 elettroni con spill out: x = y = z

0.5 1.0 1.5 2.0 2.5 3.0 0.2

0.4 0.6 0.8

(b) 2 elettroni con/senza spill out, normaliz-zata a 1: y = z = π/2 0.5 1.0 1.5 2.0 2.5 3.0 0.5 1.0 1.5 2.0 2.5 (c) 22 elettroni; x = y = z 0.5 1.0 1.5 2.0 2.5 3.0 0.2 0.4 0.6 0.8 1.0 (d) 22 elettroni; y = z = π/2

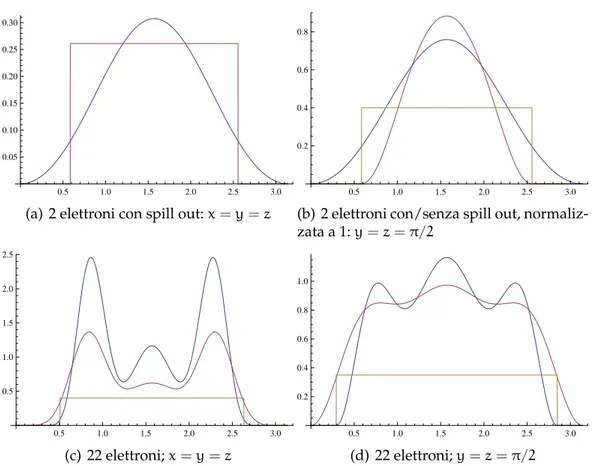
Figura 6.4:Confronto di densità elettronica con/senza spill out: nelle figure

(a) e (b) il caso a due elettroni, nelle successive due il caso a 22 elettroni. La scatola è normalizzata a π. Nei grafici di confronto la funzione senza spill out è in azzurro. Abbiamo inoltre riportato per chiarezza il profilo a scalino del jellium

6.2 CALCOLO DELLE ENERGIE IN ASSENZA DI SPILL OUT 56

sostanziale, oltre ad un diverso controllo per la convergenza, è che noi non imponiamo l’occupazione di orbitali particolari, ma scegliamo quel-li con energia minore; questo ci permette sia di scegquel-liere un autostato di energia più bassa, sia di evitare situazioni in cui la differenza di energia HOMO − LUMO(rispettivamente Highest Occupied Molecular Orbital e Lo-west Unoccupied Molecular Orbital) sia negativa, come ad esempio ottenuto per 96 e 150 elettroni. Al contempo la nostra scelta ci pone due problemi:

• La convergenza può essere molto più lenta o assente, a causa della presenza di livelli energetici molto vicini tra loro; abbiamo rilevato come questo accada usando soprattutto per i cluster più grandi (con più di 100 elettroni) e usando la densità reale dell’oro.

• A volte calcoli effettuati con un numero di basi differenti danno una diversa struttura elettronica ed i risultati ottenuti non risultano in questo modo facilmente paragonabili: questo è tuttavia un proble-ma che dovrebbe sparire all’aumentare del numero di basi, dato che per numero di basi crescenti dovremmo individuare in maniera più efficace il reale minimo energetico. Come esempio di questo proble-ma può considerare il caso a 64 elettroni illustrato nella tabella 6.2: la configurazione elettronica più esterna è 3A2

1g3T1u6 3T2g6 4T1u6 per il cal-colo con 60 funzioni di base, 3A2

1g3T1u6 4T1u6 3T2g6 per il calcolo con 87 funzioni di base e 3T6 1u3A 2 1g1T 6 1g2T 6

2gper i casi a 133 e 178 funzioni di base, con le differenze di energie HOMO-LUMO che si riferiscono a orbitali diversi.

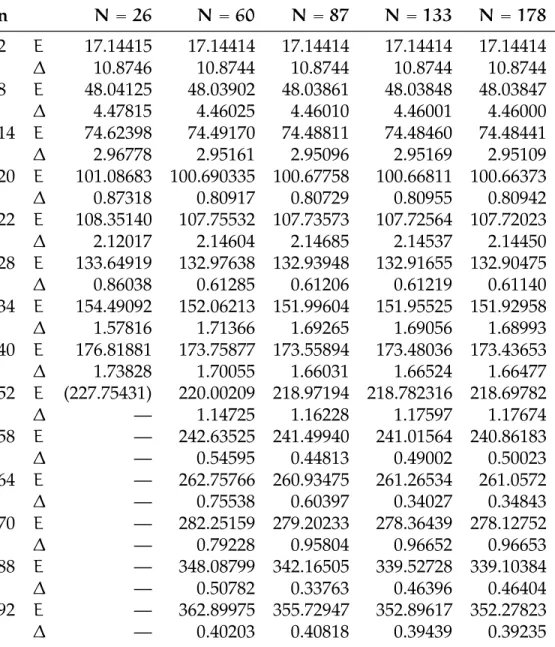
Nonostante le differenze tra i modelli, il confronto tra le energie otte-nute da noi e da Ghosh è eccellente, con differenze minori dello 0.001%, senza considerare i casi in cui la configurazione elettronica è differente. Lo stesso accordo è presente anche in alcuni casi con densità diversa da 1, non presenti nell’articolo [36] ma comunicatici in forma privata dall’autore. I calcoli di energia sono stati effettuati con diverso numero di funzione di base: abbiamo usato basi formate da 26, 60, 87, 133 e 178 funzioni di base, che corrispondono rispettivamente alle funzioni di base in cui la somma dei quadrati dei loro coefficienti mx, my, mzdell’espressione 4.1 (valore di aspettazione dell’operatore energia cinetica sulle funzioni di base) sia ri-spettivamente minore di 20, 30, 40, 50 e 60. Naturalmente si avranno dei risultati tanto migliori quanto estesa sarà la base utilizzata per i calcoli: si noti a questo proposito come il risultato dell’energia per il calcolo a 52 elettroni e 26 funzioni di base (senza cioè avere a disposizione orbitali vir-tuali) sia chiaramente inadatto e molto differente rispetto agli altri; si noti

6.2 CALCOLO DELLE ENERGIE IN ASSENZA DI SPILL OUT 57 n N = 26 N = 60 N = 87 N = 133 N = 178 2 E 17.14415 17.14414 17.14414 17.14414 17.14414 ∆ 10.8746 10.8744 10.8744 10.8744 10.8744 8 E 48.04125 48.03902 48.03861 48.03848 48.03847 ∆ 4.47815 4.46025 4.46010 4.46001 4.46000 14 E 74.62398 74.49170 74.48811 74.48460 74.48441 ∆ 2.96778 2.95161 2.95096 2.95169 2.95109 20 E 101.08683 100.690335 100.67758 100.66811 100.66373 ∆ 0.87318 0.80917 0.80729 0.80955 0.80942 22 E 108.35140 107.75532 107.73573 107.72564 107.72023 ∆ 2.12017 2.14604 2.14685 2.14537 2.14450 28 E 133.64919 132.97638 132.93948 132.91655 132.90475 ∆ 0.86038 0.61285 0.61206 0.61219 0.61140 34 E 154.49092 152.06213 151.99604 151.95525 151.92958 ∆ 1.57816 1.71366 1.69265 1.69056 1.68993 40 E 176.81881 173.75877 173.55894 173.48036 173.43653 ∆ 1.73828 1.70055 1.66031 1.66524 1.66477 52 E (227.75431) 220.00209 218.97194 218.782316 218.69782 ∆ — 1.14725 1.16228 1.17597 1.17674 58 E — 242.63525 241.49940 241.01564 240.86183 ∆ — 0.54595 0.44813 0.49002 0.50023 64 E — 262.75766 260.93475 261.26534 261.0572 ∆ — 0.75538 0.60397 0.34027 0.34843 70 E — 282.25159 279.20233 278.36439 278.12752 ∆ — 0.79228 0.95804 0.96652 0.96653 88 E — 348.08799 342.16505 339.52728 339.10384 ∆ — 0.50782 0.33763 0.46396 0.46404 92 E — 362.89975 355.72947 352.89617 352.27823 ∆ — 0.40203 0.40818 0.39439 0.39235

Tabella 6.2: Energia E e gap HOMO-LUMO ∆ in approssimazione RHF al

variare della dimensione della base N e del numero di elettroni n. Densità elettronica=1

6.3 CALCOLO DI POLARIZZABILITÀ 58

inoltre come i calcoli a 133 e 178 funzioni di base, in cui sono presenti molti orbitali virtuali, siano sempre in eccellente accordo reciproco.

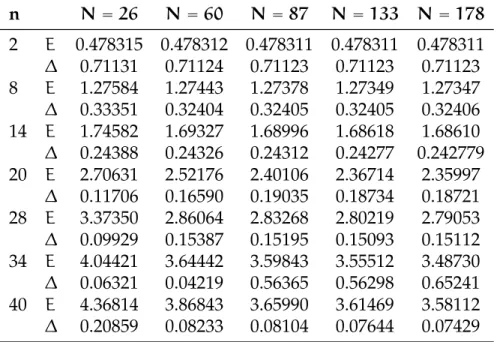
Calcoli utilizzando la densità dell’oro sono risultati molto più sensibili alle dimensioni della base utilizzata e anche la convergenza è estremamen-te rallentata: mentre per ρ = 1 il numero di iestremamen-terazioni di self consisestremamen-tenza è quasi sempre minore di 10, nel caso di ρ = 8.7541 · 10−3_{si assesta intorno} a 30 − 40. Nella tabella 6.3 riportiamo alcuni dei dati ottenuti per i cluster di piccole dimensioni. n N = 26 N = 60 N = 87 N = 133 N = 178 2 E 0.478315 0.478312 0.478311 0.478311 0.478311 ∆ 0.71131 0.71124 0.71123 0.71123 0.71123 8 E 1.27584 1.27443 1.27378 1.27349 1.27347 ∆ 0.33351 0.32404 0.32405 0.32405 0.32406 14 E 1.74582 1.69327 1.68996 1.68618 1.68610 ∆ 0.24388 0.24326 0.24312 0.24277 0.242779 20 E 2.70631 2.52176 2.40106 2.36714 2.35997 ∆ 0.11706 0.16590 0.19035 0.18734 0.18721 28 E 3.37350 2.86064 2.83268 2.80219 2.79053 ∆ 0.09929 0.15387 0.15195 0.15093 0.15112 34 E 4.04421 3.64442 3.59843 3.55512 3.48730 ∆ 0.06321 0.04219 0.56365 0.56298 0.65241 40 E 4.36814 3.86843 3.65990 3.61469 3.58112 ∆ 0.20859 0.08233 0.08104 0.07644 0.07429

Tabella 6.3: Energia E e gap HOMO-LUMO ∆ in approssimazione RHF al

variare della dimensione della base N e del numero di elettroni n. Densità elettronica ρ = 0.008754

.

6.3

Calcolo di polarizzabilità

Per questo calcolo si ritrovano alcuni dei temi riportati nel capitolo pre-cedente: abbiamo calcolato la polarizzabilità di cluster in approssimazione TDHF ed MP2 al variare del numero di elettroni e del numero di funzio-ni di base; anche in questo caso abbiamo notato una variabilità al variare della dimensione della base per ρ = 1 rispetto a ρ = 8.7541 · 10−3_.

In letteratura si trova che i calcoli di tipo Hartree-Fock con jellium sot-tostimano di circa il 20% il risultato sperimentale: purtroppo il modello

6.4 L’EFFETTO DELLO SPILL OUT 59

da noi sviluppato si è rivelato ancora più inadatto, mostrando grosse de-ficienze anche nei confronti del risultato classico. Nella tabella 6.4 ripor-tiamo i risultati al variare del numero di elettroni per ρ = 1: il confronto con il risultato classico è quasi immediato, in quanto il volume del cluster equivale numericamente al numero di elettroni del sistema. Come si vede, nel caso più eclatante, cluster con 2 elettroni, il nostro modello tiene con-to solamente circa del 4% del risultacon-to classico; all’aumentare del numero di elettroni l’errore diminuisce, ma rimane sempre al di sotto del 40% del risultato classico.

Per la densità dell’oro i risultati migliorano leggermente, ma il trend generale rimane lo stesso: per 2 elettroni la polarizzabilità è al 16% del risultato classico, con la percentuale che migliora fino ad arrivare al 52% per i cluster più grandi.

Possiamo notare come il calcolo della polarizzabilità sia molto più sen-sibile alla dimensione della base utilizzata rispetto a quantità come l’ener-gia e la differenza HOMO-LUMO: si avvertono divergenze apprezzabili quando il numero di orbitali virtuali diventa minore degli orbitali occupa-ti; nella prima colonna delle tabelle 6.4 e 6.5 si vede come la polarizzabi-lità aumenti di valore, raggiunga il suo massimo intorno ai 30 elettroni e poi diminuisca: questa diminuzione, fisicamente scorretta per una quanti-tà estensiva come la polarizzabiliquanti-tà, è sintomo della mancanza di orbitali virtuali con cui costruire stati eccitati del sistema.

I confronti riportati con il metodo MP2 sono effettuati con un nume-ro di base “ottimale”, cioè la base più piccola tra quelle utilizzate che ci consentisse di avere a disposizione un numero di orbitali virtuali maggio-re del numero di orbitali occupati; questa scelta ci consente di avemaggio-re una polarizzabilità attendibile senza dilatare eccessivamente i tempi di calcolo. Dal confronto possiamo notare come le polarizzabilità calcolate con metodo MP2 per ρ = 1 confermino i dati calcolati col il metodo TDHF, risultando comunque sistematicamente leggermente inferiori al dato cor-rispondente con lo stesso numero di basi; c’è maggiore discrepanza invece per ρ = 0.008754, probabilmente per il diverso peso della correlazione elettronica a densità minori.

6.4

L’effetto dello spill out

L’effetto dello spill out è quello di aumentare il volume a disposizione della carica elettronica, non lasciandola confinata all’interno del volume del jellium, come è costretta dalle caratteristiche del modello, ma

lascian-6.4 L’EFFETTO DELLO SPILL OUT 60 n 26 60 87 133 178 MP2 2 0.02061 0.02061 0.02061 0.02061 0.02061 0.02059 8 0.28576 0.29035 0.29043 0.29048 0.29051 0.27920 14 0.61663 0.64430 0.64481 0.64548 0.64584 0.62822 20 1.08751 1.16728 1.17456 1.17691 1.17820 1.10018 22 1.32815 1.45451 1.46628 1.46986 1.47164 1.39358 28 1.73265 2.05802 2.09549 2.10712 2.11145 2.02463 34 2.17139 2.70751 2.78807 2.81550 2.82352 2.70192 40 1.22330 2.83900 2.96823 2.99913 3.00969 2.81557 52 (0) 4.71859 5.08405 5.26191 5.30604 4.62091 58 — 5.63572 5.83636 5.74449 5.77564 5.78132 64 — 5.65390 6.25763 6.73491 7.03645 6.54612 70 — 6.50184 7.13315 7.5456 7.66855 7.3160 88 — 8.57757 8.98128 9.67433 10.01849 8.72146 92 — 5.71549 9.17283 10.23598 10.84100 9.77135

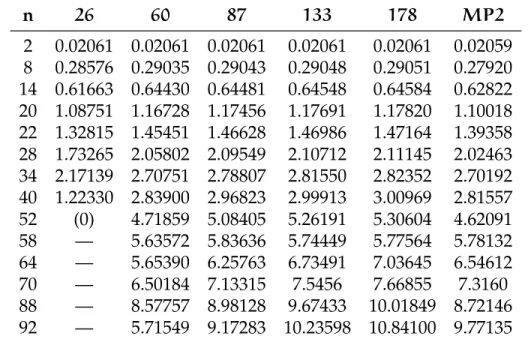
Tabella 6.4:Polarizzabilità statica α in approssimazione TDHF al variare

del-la dimensione deldel-la base N e del numero di elettroni n; nell’ultima colonna è riportato un calcolo MP2 a numero di basi variabile. Densità elettronica ρ = 1

. V 26 60 87 133 178 MP2 228 9.1026 9.1043 9.1052 9.1054 9.1054 9.025 913 82.344 89.248 92.884 93.69341 93.937 77.375 1599 160.188 177.695 180.573 181.780 182.438 147.443 2284 233.955 248.925 253.421 257.321 259.004 261.920 2513 277.778 302.653 338.301 341.308 343.936 273.001 3198 365.018 409.381 427.799 445.708 451.059 374.614 3884 339.451 528.105 571.734 588.641 594.994 475.627 4571 240.486 569.463 646.834 661.553 667.355 570.882 5485 73.611 581.003 679.781 696.126 703.154 613.504

Tabella 6.5:Polarizzabilità statica α in approssimazione TDHF al variare

del-la dimensione deldel-la base N e del volume V; nell’ultima colonna è indicato un calcolo MP2 a numero di basi variabile. Densità elettronica ρ = 0.008754

6.4 L’EFFETTO DELLO SPILL OUT 61

dola fuoriuscire.

Il valore che tipicamente si ottiene da simulazioni numeriche per clu-ster metallici è compreso tra 1.2 e 2: noi abbiamo usato il valore 1.4ua, come suggerito da diverse fonti [6, 24, 31].

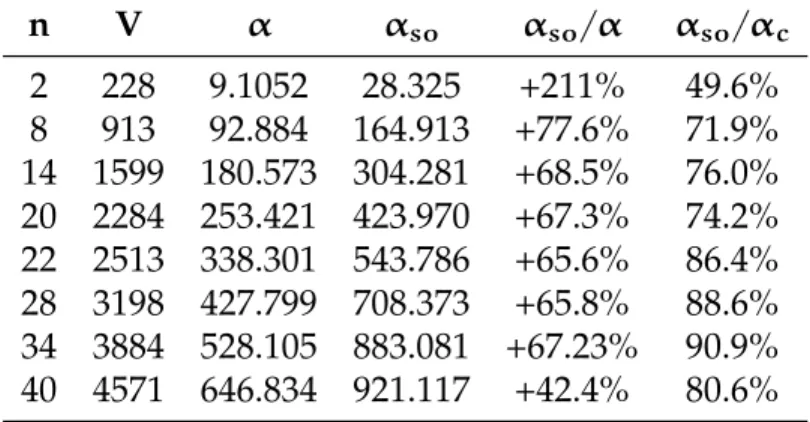
L’introduzione di questo parametro migliora notevolmente i valori pre-cedenti, soprattutto per i cluster più piccoli, dove l’aumento di volume è percentualmente più significativo. Riportiamo nella tabella 6.6 i risultati al variare delle funzioni di base per alcuni cluster di piccole dimensioni.

n V α αso αso/α αso/αc 2 228 9.1052 28.325 +211% 49.6% 8 913 92.884 164.913 +77.6% 71.9% 14 1599 180.573 304.281 +68.5% 76.0% 20 2284 253.421 423.970 +67.3% 74.2% 22 2513 338.301 543.786 +65.6% 86.4% 28 3198 427.799 708.373 +65.8% 88.6% 34 3884 528.105 883.081 +67.23% 90.9% 40 4571 646.834 921.117 +42.4% 80.6%

Tabella 6.6: Confronto tra polarizzabilità α e αso in assenza e in presenza

di spill out per 87 funzioni di base. È indicato il miglioramento percentua-le del caso con lo spill out e il rapporto con il risultato classico αc. Densità

elettronica ρ = 0.008754

Come possiamo vedere si ha un netto miglioramento dei risultati, che si mantengono però ancora non sufficientemente vicini ai risultati speri-mentali.

Il caso a due elettroni, il peggiore nel caso senza spill out, è come ci aspettavamo quello che ha maggiori benefici dall’estensione del modello, aumentando di più di 3 volte la propria polarizzabilità. L’effetto positivo diminuisce a mano a mano che aumenta il numero di elettroni, ma rimane comunque importante, intorno al 60%.

Tuttavia, nonostante il miglioramento dei risultati, una descrizione del-lo spill out come quella usata in questa tesi non riesce a tenere conto in ma-niera adeguata dell’andamento delle autofunzioni all’esterno della carica positiva.

Un andamento realistico darebbe una diminuzione esponenziale della densità di carica all’esterno del volume del jellium, con un valore finito della carica elettronica esterna al volume: una descrizione di questo tipo

6.5 POLARIZZABILITÀ DINAMICA: QUALCHE RISULTATO 62

non può essere raggiunta dal nostro modello con poche funzioni di base di tipo trigonometrico.

Per illustrare questo problema abbiamo effettuato calcoli su di un clu-ster in cui il volume di spill out è stato via via aumentato da 0 a 9 unità ato-miche: la carica esterna al jellium tende ad aumentare senza stabilizzarsi, e lo stesso avviene per la polarizzabilità. In un modello stabile dovremmo assistere ad una convergenza al valore reale della carica esterna, che sarà sicuramente raggiunto anche dal nostro modello, ma probabilmente con un numero di funzioni tale da non renderne conveniente l’uso.

6.5

Polarizzabilità dinamica: qualche risultato

Per il calcolo della polarizzabilità dinamica abbiamo utilizzato un riar-rangiamento delle formule indicate nel capitolo 3, riportate in dettaglio da [43], che ci ha permesso di identificare i poli della polarizzabilità, corri-spondenti alle frequenze di transizione di dipolo ωi.

La polarizzabilità dinamica può essere scritta come α(ω) =X

i

fi ω2_{− ω}2

i

dove le fisono dette forze dell’oscillatore, per le quali valgono diverse regole di regola di somma [44, 28], tra cui quella di Thomas-Khun [44]:P_ifi= N, con N il numero degli elettroni.

Abbiamo verificato che la regola di somma di Thomas-Khun è sod-disfatta entro un buon margine di incertezza, entro pochi punti percen-tuali, e con precisione crescente all’aumentare delle dimensioni della base utilizzata.

Il metodo che abbiamo utilizzato ci dà un numero molto elevato di fre-quenze di transizione, dipendente dal numero di funzioni di base N e dal numero di elettroni 2n come n(N − n). Abbiamo verificato che tipicamen-te, comunque, solo pochi tra questi picchi hanno intensità importanti ed essi esauriscono gran parte della regola di somma.

Le frequenze di assorbimento collettive principali di un cluster sferico sono di solito due, corrispondenti (macroscopicamente) alle frequenza di plasmone di volume e di superficie [1]; Kresin, ad esempio, nella tratta-zione indicata nel primo capitolo utilizza solo queste due frequenze per la descrizione della polarizzabilità. Considerazioni su cluster cubici [45, 46] trovano una separazione del modo plasmonico superficiale sferico in più picchi distinti, ma non variano significamente le frequenze in gioco.

6.6 CONSIDERAZIONI FINALI 63

I risultati da noi ottenuti numericamente per cluster in assenza di spill out anche in questo caso hanno pochi riscontri con i risultati teorici e spe-rimentali: per cluster di due elettroni una singola frequenza copre il 96% delle regole di somma per ω = 0.79, mentre per cluster più grandi c’è una frequenza principale per ω = 1.16 attorno alle quali si sviluppano i picchi di intensità maggiore (2 o 3 a seconda dei casi); tuttavia queste frequenze non corrispondono al valore numerico della frequenza di plasma per l’oro, nè per quelle di plasmone superficiale, .

Per calcoli in presenza di spill out si assiste ad uno shift delle frequenze, dovuto al fatto che le dimensioni della nuvola elettronica sono differenti: anche in questo caso tuttavia non si hanno riscontri con i dati di letteratura.

6.6

Considerazioni finali

I risultati di questo lavoro di tesi sono divisi in due parti: la prima ana-lizza un modello di cluster approssimato da un jellium cubico su cui è libera di interagire la carica elettronica. Un calcolo di questo tipo, chiara-mente insufficiente, è servito da base e da confronto per lo sviluppo di un modello leggermente più complesso, in cui venisse inserito un parametro “fenomenologico” come lo spill out, che mantenesse però le caratteristiche di semplicità del calcolo iniziale.

La velocità di calcolo del nostro modello è sicuramente uno dei punti di forza: è necessario un investimento iniziale (circa 23 ore di tempo di calcolo) per calcolare numericamente con il metodo di Gauss-Legendre a 320 punti tutti gli integrali (p|q) necessari ad un calcolo per basi fino a 343 funzioni di base, ma i calcoli successivi, grazie all’uso delle simmetria del sistema, sono estremamente veloci: per un calcolo della polarizzabilità con 26elettroni di base, sufficiente per i cluster più piccoli, sono necessari solo pochi secondi; per i cluster più grandi ed una base di 178 funzioni sono mediamente necessari meno di 18 minuti.

Il trattamento effettuato per permettere agli elettroni di fuoriuscire dal-la carica del jellium può essere inoltre generalizzato: grazie al principio di sovrapposizione dei campi [17] possiamo considerare modelli in cui la densità del jellium sia radialmente diversa in diversi punti (ad esempio ρ0 per 0 ≤ x, y, z ≤ δ1, ρ1per δ1≤ x, y, z ≤ δ2, . . . , ρnper δn≤ x, y, z ≤ π/2). Il numero di integrali supplementare per n scalini è pari a 120(n−1) per un numero di basi fino a 343; un modello di questo tipo ci permetterebbe di considerare con minimo sforzo cluster in cui la carica nucleare non è uni-forme sul volume, oppure cluster con atomi di diverso numero atomico all’interno e all’esterno.

6.6 CONSIDERAZIONI FINALI 64

Questi elementi positivi sono però purtroppo controbilanciati da una inefficace descrizione delle caratteristiche ottiche del sistema: le nostre aspettative durante la stesura dei programmi erano di ottenere una descri-zione della polarizzabilità paragonabile a quella ottenuta da altri calcoli si-mili, come ad esempio [15, 25, 41, 47]; il nostro modello si è rivelato invece inadeguato, soprattutto considerando che non riesce a riprodurre nemme-no il caso classico. Riteniamo che le proprietà basilari del sistema, quali l’energia e le differenze HOMO-LUMO siano calcolate in modo sufficien-temente preciso, mentre per le proprietà ottiche del sistema sia preferibile riferirsi a calcoli di tipo diverso.