6
6
S
S
i
i
m
m
u
u
l
l
a
a
z
z
i
i
o
o
n
n
e
e
d
d
e
e
l
l
m
m
o
o
d
d
e
e
l
l
l
l
o
o
c
c
o
o
n
n
v
v
o
o
l
l
u
u
t
t
i
i
v
v
o
o
p
p
e
e
r
r
s
s
e
e
g
g
n
n
a
a
l
l
i
i
f
f
M
M
R
R
I
I
6.1 Costruzione del modello
er verificare l’applicabilità del modello convolutivo a situazioni reali e valutarne l’efficacia, ci possiamo costruire un prototipo simulante ciò che accade in uno o più voxel attivati a seguito di una stimolazione.
In primo luogo dobbiamo simulare un “paradigma” di stimolazione e la scelta cade su un treno di onde quadre (di periodo T=50 secondi, ampiezza A=2, duty cycle pari a ½ e valor medio nullo) imitante una stimolazione sensoriale con analoghe caratteristiche temporali a cui viene sottoposto un ipotetico paziente. Assumendo poi valido il modello lineare [22-26] possiamo ricavare la risposta fMRI semplicemente convolvendo il nostro paradigma con la funzione di trasferimento del sistema-voxel, così come visto nel capitolo 1. Come funzione di trasferimento (SI) si è scelto di utilizzare quella proposta da Cohen, che richiama l’andamento di una funzione gamma e qui riproposta per maggior chiarezza:
) /
exp( t b
kt
SI = a − (5.1)
dove a = 8.60 e b = 0.547 e il cui andamento è evidenziato in figura 5.1.
Fig. 5.1 Risposta impulsiva del voxel
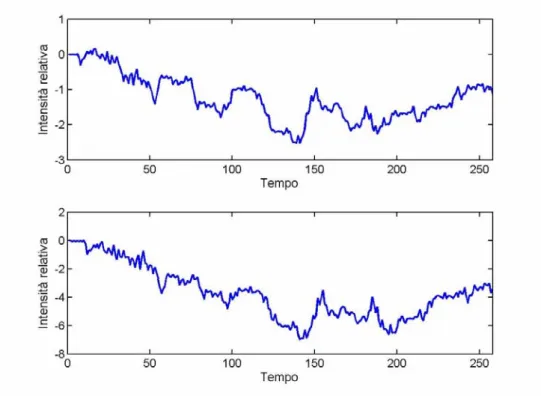
A questo punto la risposta attesa risulta la convoluzione del paradigma di stimolazione con la (5.1). Nelle acquisizioni tipiche il tempo di ripetizione TR (tempo necessario ad acquisire i dati provenienti da una slice cerebrale e quindi tempo che intercorre tra una acquisizione e la successiva) è dell’ordine di qualche secondo, per questo si è scelto di sottocampionare il segnale risultante dalla convoluzione, in modo tale da ottenere una sequenza temporale verosimile, mostrata in figura 5.2 in basso.
Come secondo segnale (figura 5.2 in alto) in ingresso al nostro sistema si è scelto un effettivo andamento temporale attribuibile ad artefatti (dovuti a movimenti del paziente).
Fig 5.2 Segnali di ingresso
6.2 Deconvoluzione nel dominio del tempo
Il nostro scopo è ora valutare gli effetti convolutivi del canale (vale a dire del mezzo cerebrale in cui si originano e si propagano i segnali) riuscendo possibilmente ad isolare il segnale utile dagli artefatti. Ulteriormente sarebbe auspicabile riuscire a stimare lo sfasamento introdotto dal mezzo convolutivo, che come sappiamo fornisce utili informazioni sul ritardo emodinamico.
Per simulare gli effetti del canale si è usato una matrice H(z) di dimensione 2×2×12, in cui ogni elemento rappresenta un filtro FIR di
ordine 12, come evidenziato in figura 5.3. I filtri sono stati scelti di tipo passa basso, a fase lineare, frequenza di taglio normalizzata pari a 0.9 e modulo arbitrario in modo tale da provocare nel canale uno sfasamento relativo dei segnali pari a circa 4 secondi. In figura 5.3 si nota infatti che i vari elementi della matrice di convoluzione risultano reciprocamente sfasati in modo tale da ottenere l’effetto desiderato.
Fig. 5.3 Matrice di convoluzione
In base alla (4.15) si possono ora valutare i segnali misurati, quelli cioè che escono convoluti e reciprocamente ritardati dal nostro canale, come è rappresentato in figura 5.4.
Per procedere ora alla ricerca delle sorgenti originarie e in particolar modo del segnale utile rappresentato dalla risposta fMRI modellata, l’ipotesi di fondo che si deve fare è l’indipendenza statistica delle sorgenti. Nello
specifico, volendo applicare un metodo deconvolutivo, nel dominio del tempo, basato sulla minimizzazione di una funzione costo e sfruttando la regola del gradiente naturale, si ricercherà l’indipendenza minimizzando la mutua informazione secondo la (4.61).
Fig. 5.4 Segnali osservati
Prima di applicare l’algoritmo di separazione risulta utile effettuare un’operazione di sbiancamento dei dati senza riduzione di dimensionalità del problema. Ciò ci permette, come già ricordato nel capitolo 3, di diminuire il numero di parametri da computare.
Ulteriori accorgimenti sono stati presi in fase di inizzializzazione dell’algoritmo in modo da evitare soluzioni spurie e a questo riguardo si è scelto di imporre che il valore al passo iniziale della matrice di deconvoluzione W, espressa dalla (4.76), sia pari al valore della matrice identica come suggerito in [15].
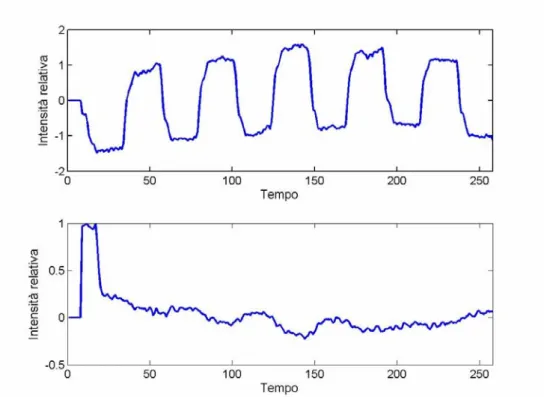
Il risultato della separazione delle sorgenti iniziali è mostrato in figura 5.5, dove si rileva che l’algoritmo riesce apprezzabilmente ad evidenziare l’andamento del paradigma di attivazione cercato, ma non giunge a separare completamente gli artefatti.
Fig. 5.5 Segnali deconvoluti
Come indice numerico indicante la bontà del risultato possiamo valutare il coefficiente di correlazione tra l’inviluppo deconvoluto e la sorgente iniziale, ottenendo: 892 . 0 ≈ = j i ij ij s s s r (5.2)
dove si è la deviazione standard del vettore i-esimo che rappresenta uno
dei due segnali.
La fig. 5.5 indica anche l’ambiguità che, qui così come per la BSS istantanea, affligge il modello e cioè l’indeterminazione del fattore di scala dovuto al fatto che comunque non è possibile determinare le energie delle componenti indipendenti.
A questo punto ci chiediamo se sia possibile recuperare le informazioni riguardanti lo sfasamento introdotto dalla convoluzione e dai filtri FIR utilizzati. In quest’ottica risulta utile considerare apertamente la natura multicanale dei segnali acquisiti e cioè valutare i contributi delle sorgenti indipendenti nei vari canali di filtraggio. Nella nostra simulazione abbiamo una sola componente utile (l’altra è, come abbiamo visto, un artefatto) filtrata da un mezzo bi-canale, il cui effetto è generare campioni ritardati che arrivano pertanto mischiati in punti diversi sul segnale rilevato.
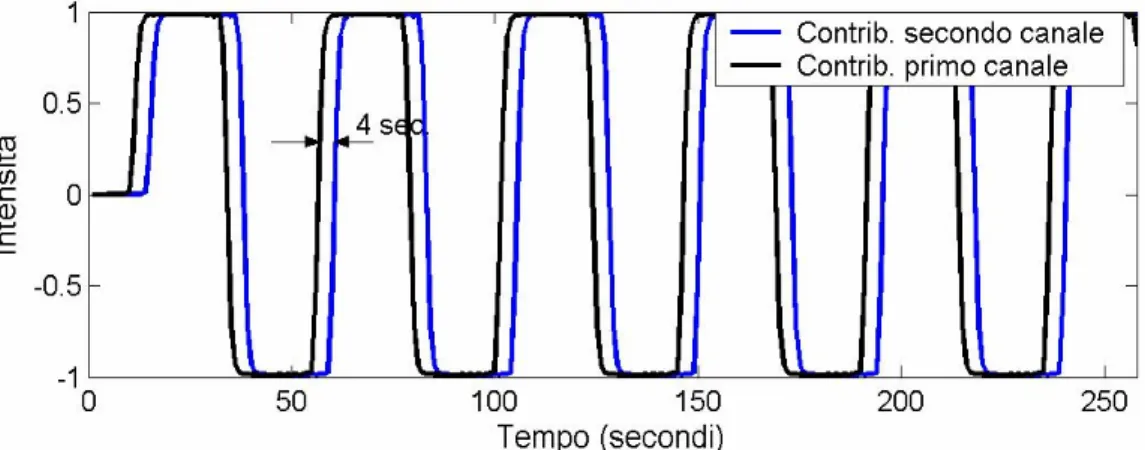
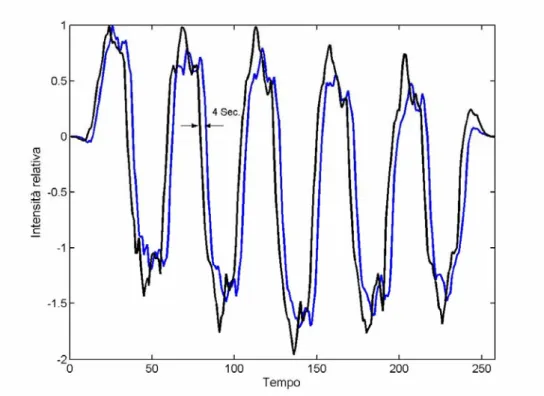
In figura 5.6 sono rappresentati i contributi normalizzati del paradigma di attivazione all’uscita del primo canale (linea nera) e del secondo canale (linea blu) così come sarebbero osservati se non ci fosse l’artefatto in ingresso.
Come si può apprezzare i due segnali risultano ritardati reciprocamente di circa 4 secondi a causa dell’effetto del filtraggio.
La valutazione sulla performance dell’algoritmo nel dominio temporale si conclude, quindi, nel valutare qualitativamente e quantitativamente (attraverso l’algoritmo proposto in appendice) se la sopraccitata informazione sullo sfasamento dei segnali viene riportata in uscita dai segnali deconvoluti e ricostruiti. Ricostruire significa filtrare il segnale deconvoluto attraverso i filtri di deconvoluzione stimati W(z), in modo tale da poter fare un raffronto diretto (vedi figura 5.7) tra i segnali osservati (xi(t)) e i segnali ricostruiti (xi' t( )).
Fig. 5.7 Diagramma a blocchi dell’operazione da eseguire
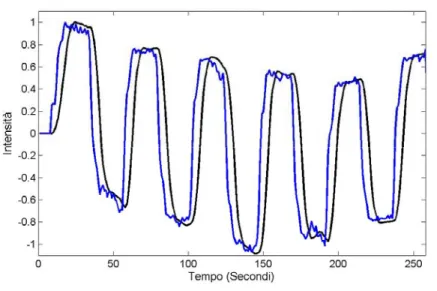
I risultati del confronto sono visibili in figura 5.8 di pagina seguente in cui è evidente come questo tipo di deconvoluzione non permette di recuperare l’esatta informazione relativa allo sfasamento temporale indotto dal canale, tuttavia è capace di fornire informazioni sulle dinamiche temporali dei segnali. Sovrapponendo infatti i segnali ricostruiti sui rispettivi canali si evidenzia uno sfasamento compatibile con quello introdotto dal canale medesimo e valutabile in 4.2 sec (per i metodi di stima dello sfasamento vedere appendice). H(z) CONFRONTO W(z) s(t) y(t) x’(t) x(t) ⊗
Fig. 5.8 Sovrapposizione tra i segnali ricostruiti sui rispettivi canali e loro reciproco sfasamento
6.3 Deconvoluzione nel dominio della frequenza
Nel tentativo di ottenere un’informazione più precisa sul ritardo, vediamo allora di provare l’algoritmo di BSS convolutiva nel dominio frequenziale descritto nel capitolo 4. Il modello usato per stimare la risposta fMRI rimane il solito, così come identici restano le considerazioni sui filtri convolutivi e le ipotesi sull’indipendenza statistica delle sorgenti.
Operativamente inoltre va valutato che la larghezza della finestra su cui si esegue la STFT è un compromesso tra la risoluzione temporale e frequenziale che vogliamo ottenere, così come il numero di campioni usati non può essere inferiore all’ordine dei filtri utilizzati. Viene infatti effettuata la trasformata discreta di Fourier dei segmenti dei segnali xi(t) e, lavorando
in frequenza, si deve supporre che il numero di matrici di mescolamento che stiamo cercando non sia maggiore dei campioni di frequenza a disposizione. Infine l’algoritmo di separazione delle componenti indipendenti in frequenza è l’algoritmo FastICA descritto nel capitolo 3.
Valutando direttamente il contributo della risposta utile e degli artefatti sui due canali deconvulutivi si può vedere (figura 5.9) come anche questo approccio “rintracci” il paradigma fMRI ma sia meno accurato nell’estrarre la componente relativa agli artefatti. Quest’ultima considerazione tuttavia non c’è d’alcun ostacolo, poiché il nostro fine risulta la stima del ritardo introdotto dal mezzo convolutivo, stima sulla quale il criterio nel dominio temporale ha mostrato di fallire.
Fig. 5.9 Contributi delle componenti deconvolute nei rispettivi canali. Segnale utile in alto,
Sovrapponendo quindi i contributi in uscita dal canale convolutivo con i rispettivi segnali deconvoluti, ricostruiti e normalizzati nei rispettivi canali si può valutare l’informazione relativa al ritardo temporale. Una prima indicazione positiva arriva subito dal confronto tra i due segnali ricostruiti in uscita evidenziati in figura 5.10.
Fig. 5.10 Reciproco sfasamento dei segnali ricostruiti in uscita
Questi due segnali risultano reciprocamente sfasati e l’entità di tale sfasamento è confrontabile con il reale ritardo introdotto dal canale convolutivo. Nel punto indicato dalle due frecce, ad esempio, lo sfasamento equivale esattamente a 4 secondi (vedere appendice), quantità che ci si era imposti di ritrovare a partire dalla figura 5.6. Utilizzando l’algoritmo proposto in appendice si ritrova infatti un ritardo temporale tra i due segnali pari a 3.95 secondi. Una ulteriore conferma della bontà di tale stima
è mostrata in figura 5.11 in cui i segnali ricostruiti e normalizzati sono sovrapposti ai rispettivi contributi del canale convolutivo.
Fig. 5.11 Sovrapposizione incrociata tra i contributi in uscita dal canale convolutivo (linea
intera) ed i segnali ricostruiti (linea tratteggiata).
Nella figura sopra riportata si nota che, a seconda del canale considerato, i segnali ricostruiti risultano in anticipo o in ritardo di una quantità temporale ragionevolmente confrontabile con il ritardo da noi imposto con l’operazione di filtraggio convolutivo e pari a 4 secondi.
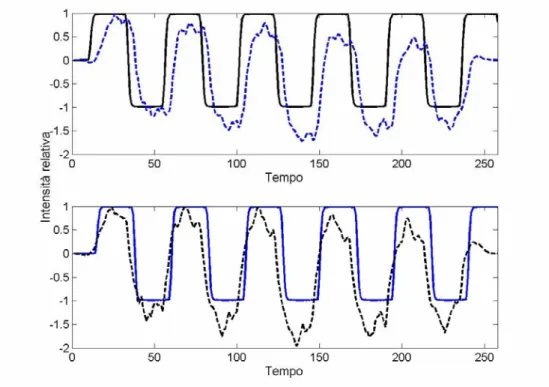
Infine, calcolando il coefficiente di correlazione tra i segnali ricostruiti in uscita e i corrispondenti segnali filtrati convolutivamente si ottiene un indicatore del risultato raggiunto. Un valore di 0.89 per il caso rappresentato in alto in figura 5.12 e un valore di 0.93 per quello rappresentato in basso è indice di una ricostruzione quanto mai fedele (si
ricorda che il coefficiente di correlazione vale al massimo 1 e in tale caso questo valore significa assoluta correlazione tra i due segnali).
Fig. 5.12 Confronto tra i contributi in uscita del canale convolutivo (linea intera) e i segnali
ricostruiti sui canali corrispondenti (linea tratteggiata).
6.4 Valutazione dell’accuratezza della deconvoluzione
Quale indicatore dell’accuratezza dei risultati ottenuti sia nel dominio temporale che in quello frequenziale, si è scelto di utilizzare il Noise Reduction Rate (NRR). Tale indice è definito [29] come la differenza tra il rapporto segnale-rumore (SNR) espresso in dB dell’output e il rapporto segnale-rumore dell’input. L’output è rappresentato ovviamente dalle componenti indipendenti deconvolute mentre l’input sono i segnali
sorgente che si è interessati ad individuare, perciò il nostro indice (definito per due sorgenti) è esprimibile come:
) ( 2 1 ( ) 2 1 ) ( I l l O l SNR SNR NRR=
∑
− = (5.2)dove si assume che le sorgenti indesiderate in ogni canale sono da considerarsi rumore. I due valori del SNR presenti nella (5.2) sono quindi definibili come:
∑
∑
∑
∑
= = f n f ll l I l f n f ll l O l f S f H f S f H SNR f S f C f S f C SNR 2 ln 2 10 ) ( 2 ln 2 10 ) ( ) ( ) ( ) ( ) ( log 10 ) ( ) ( ) ( ) ( log 10 (5.3)dove l≠n e SNRl(O) e SNRl( I) sono il rapporto segnale_rumore di uscita e
di ingresso rispettivamente. Sl(f) è invece la trasformata di Fourier del
segnale sorgente sl(t), mentre Hij( f) è l’elemento nella i-esima riga e
nella j-colonna della matrice C(f)=W(f)H(f), con W( f) e H( f)
rappresentazione, rispettivamente, della matrice di deconvoluzione e di mescolamento nel dominio della frequenza.
Con queste premesse la performance ottenuta dai due algoritmi di separazione usati nei paragrafi precedenti è riportata nel grafico di figura 5.13. Affinché i risultati siano più significativi si è scelto di effettuare un numero di prove usando come segnali di ingresso (oltre al segnale utile
rappresentato in figura 5.2 in basso) una serie di 10 artefatti diversi dovuti a movimento e caratterizzati attraverso la loro deviazione standard.
0 2 4 6 8 10 12 1 2 3 4 5 6 7 8 9 10 Prove N R R (N o is e R e d u c ti o n R a te ) [d B ] NRR separazione in frequenza NRR separazione nel tempo 1-> 0.0557 2-> 0.0471 3-> 0.025 4-> 0.0618 5-> 0.0417 6-> 0.069 7-> 0.05 8-> 0.013 9-> 0.087 10-> 0.074
Fig. 5.13 Performance di separazione degli algoritmi utilizzati (a destra della tabella sono
indicati i valori della deviazione standard degli artefatti).
6.5 Confronto con il modello istantaneo
Alla luce dei risultati ottenuti è interessante applicare un algoritmo di separazione istantaneo agli stessi dati simulati, usati nei precedenti paragrafi e valutarne l’abilità nell’individuare le componenti indipendenti.
In pratica si applica l’algoritmo ai segnali convoluti incontrati in figura 5.4, sfruttando la massimizzazione della neg-entropia e utilizzando come nonlinearità la tangente iperbolica analogamente a quanto è stato fatto per i processi deconvolutivi sopra esposti.
Fig. 5.14 Componenti indipendenti separate con l’algoritmo FastICA
Come si può constatare (in figura 5.12) i risultati (se paragonati ad esempio con quelli ottenuti in figura 5.5) conducono ad un evidente peggioramento nell’individuazione della componente indipendente rappresentata dal segnale in alto (coefficiente di correlazione tra sorgente iniziale e componente trovata pari a 0.29 e NRR pari a 3.06). Anzi, viene perso anche l’andamento dell’inviluppo degli artefatti (in basso) oltre al fatto che, naturalmente, risulta impossibile valutare lo sfasamento introdotto dal processo convolutivo non potendo separare i contributi sui vari canali.