CAPITOLO 4 Comportamento meccanico dei solidi cellulari

CAPITOLO 4

Comportamento meccanico dei solidi

cellulari

4.1 Definizione

Le schiume sintattiche vengono classificate anche come una particolare classe di solidi cellulari, (da qui anche la denominazione come schiuma), classificazione che permette di valutare l’adattabilità alle schiume sintattiche in dei modelli teorici di questa tipologia di materiale. Una trattazione completa dei solidi cellulari è stata effettuata da Ashby-Gibson in “Cellular Solids” [1].

Si definisce un solido a struttura cellulare, un solido costituito dall’assemblaggio nello spazio di singole unità dette celle; dove per cella si intende un elemento spaziale cavo delimitato da spigoli e facce. Molti materiali naturali, come il legno, la cellulosa, le ossa degli animali, presentano questo tipo di struttura e per questo motivo possono essere classificati come solidi cellulari. Materiali di questo tipo stati realizzati attraverso processi artificiali che partendo da un materiale a struttura compatta, permettono di realizzare strutture cellulari bidimensionali o tridimensionali. I solidi cellulari possono essere impiegati per raggiungere diversi scopi, uno dei più importanti è quello di migliorare le caratteristiche meccaniche specifiche, ovvero le caratteristiche meccaniche relative al peso specifico del materiale.

Il parametro caratteristico per definire le caratteristiche di un materiale a struttura cellulare risulta essere la densità relativa, ossia il rapporto ρ*/ρs ovvero il rapporto tra la densità del solido a struttura cellulare, e la densità del solido di partenza (4.1)

compatto solido del Densità cellulare struttura a solido del Densità * = S ρ ρ

(4.1 - Densità relativa di un solido cellulare)

Il grado di vuoto all’interno di un materiale, può essere espresso con un altro parametro strettamente legato alla densità relativa, ovvero la porosità che è espressa dalla (4. 2):

S

ρ ρ*

Questi parametri vengono ricavati sperimentalmente, tramite alcune procedure standard, e risultano particolarmente importanti perché ad essi possono essere associati direttamente quelle che sono le caratteristiche geometriche della cella, e quindi le sue proprietà meccaniche.

4.2 Classificazione dei solidi celulari

I solidi cellulari possono essere classificati in due categorie:

o Honeycomb: sono strutture cellulari caratterizzate da un array bidimensionale di celle, aventi tutte la stessa profondità e la stessa geometria della sezione, la più utilizzata in genere è la geometria esagonale, per questo motivo sono dette honeycomb o struttura a nido d’ape, come rappresentato nella figura.2.7

o Schiume: sono strutture cellulari caratterizzate da celle poliedriche disposte nello spazio in maniera generalmente casuale. Possono essere classificate come schiume (Figura 4.1), a celle aperte o a celle chiuse

o A celle aperte (open cell foams): ogni cella è costituita solo dagli spigoli (Figura 4.2) o A celle chiuse (closed cell foams): gli spigoli della cella sono connessi tra loro dalle

facce, come un vero e proprio poliedro. Generalmente la parete ha uno spessore più piccolo rispetto allo spigolo della cella. All’interno della cella rimane intrappolato del gas (Figura 4.3). Le schiume sintattiche possono essere classificate come un particolare tipo di schiuma a celle chiuse.

Figura 4.2 - Schiuma di Nichel a struttura aperta – Immagine tratta da P.S. Liu “Tensile fracture behavior of foamed metallic materials” [26]

Figura 4.3 – Schiuma di Polietilene a celle chiuse – Immagine tratta da F.Ramsteiner, N.Fell, S.Forster – “Testing the deformation behaviour of polymer foams” [27]

4.3 Caratteristiche Geometriche

Le grandezze fondamentali della geometria della cella possono essere ricondotte al:

- t : spessore di parete (cell wall thickness) - L: lunghezza di spigolo ( edge lenght)

Prendendo in esame le possibili topologie della cella è possibile determinare i parametri caratteristici del solido cellulare, densità relativa e porosità, in funzione delle caratteristiche geometriche t, L ed in particolare del loro rapporto.

La caratterizzazione della topologia di un solido a struttura cellulare è fatta attraverso un indagine micrografica, tramite la quale si può stabilire:

• Dimensioni della cella

• Tipo di forma, in particolar modo la sua anisotropia • Dispersione della forma

Infatti la densità relativa di un solido cellulare può essere espressa attraverso le caratteristiche geometriche della cella (Tabella 4.1 ). Nel caso in cui, si supera un certo limite della densità relativa, risulta opportuno aggiungere un fattore correttivo, che altrimenti è trascurabile:

Densità Relativa * 0.2 s > ρ ρ Strutture a nido d’ape C1 _Lt s * = ρ ρ       − = L t D L t C_{1 1} s 1 * ρ ρ Schiume a celle aperte 2 2 s *       = L t C ρ ρ _      − = L t D L t C_{2 2} s 1 * ρ ρ Schiume a celle chiuse C3 _Lt s * = ρ ρ       − = L t D L t C_{3 3} s 1 * ρ ρ

Tabella 4.1 – Densità relativa per le varie classi di solidi cellulari

C1,C2,C3,D1,D2,D3 sono costanti dipendenti dalla geometria della cella.

Nel caso delle schiume a celle chiuse, bisogna tener conto di un altro termine correttivo. Nella formazione della schiuma, si nota che il materiale tende a concentrarsi negli spigoli piuttosto che nelle pareti della cella, quindi per questo motivo è opportuno tenere conto di un ulteriore parametro φ, definito come frazione di volume di materiale contenuto negli spigoli.

φ è funzione delle caratteristiche topologiche della cella, rispettivamente lo spessore delle pareti, e lo spessore degli spigoli della cella.

4.4. Comportamento meccanico dei solidi cellulari

A caratterizzare il comportamento meccanico di un solido cellulare concorrono in particolar modo questi fattori:

o Geometria della cella

o Le caratteristiche meccaniche e la natura costitutiva del solido di partenza

Ad esempio il comportamento costitutivo di una schiuma ricavata da un materiale elastomerico, sarà prevalentemente elastico, ovvero presenterà meccanismi di deformazione che rimarranno fino a rottura di tipo elastico, senza mostrare deformazioni plastiche.

La tabella 4.2 riassume i meccanismi di deformazione di un solido cellulare tenendo presente la natura costitutiva del solido da cui è stato ricavato:

Modello Costitutivo Trazione Compressione

Elastico Rottura senza deformazione plastica

C’è un valore del carico oltre il quale si verifica il buckling

Elasto-Plastico Snervamento e deformazioni

plastiche raggiungere il collasso plastico del Gli spigoli si deformano fino a materiale, oppure anche in questo

caso si può avere buckling

Fragile Rottura fragile Rottura Fragile

Tabella 4.2 – Meccanismi di rottura in funzione della natura costitutiva

Particolarmente importante, visto l’impiego di questi materiali come anima in strutture a sandwich, la caratterizzazione del comportamento a compressione. In compressione, proseguendo con la deformazione, le celle iniziano a collassare l’una sull’altra, dando luogo ad un fenomeno che in [1] viene definito processo di densificazione del materiale (densification). Le curve sforzo-deformazione dipendono dalla densità relativa del materiale, maggiore è la densità relativa, maggiori sono i valori di t, L, più robusta risulta essere la singola cella e dunque più resistente diventa il materiale.

Questo meccanismo di deformazione in compressione è stato evidenziato anche nelle prove sperimentali effettuate sulla schiuma sintattica E-Foam.

4.5

Comportamento meccanico delle strutture a nido d’ape

Nella trattazione di Ashby-Gibson, viene prima discusso il comportamento di una struttura a nido d’ape con celle esagonali, per poi passare alla trattazione delle altre strutture più complicate, confrontandole sempre con il modello iniziale che risulta più semplice e comprensibile. Si distinguono due tipi di analisi per quanto riguarda lo studio del comportamento meccanico (valutazione della rigidezza e della resistenza) di una struttura a nido d’ape:

o Comportamento meccanico “In Plane” o Comportamento meccanico “Out Plane”

Tenendo presente la figura seguente (4. 5), il comportamento meccanico “In Plane” è quello relativo al piano X1 , X2 , invece per comportamento “Out Plane”, si intende il comportamento

della struttura sollecitata con carichi agenti al di fuori del piano X1 , X2.

Figura 4.5 - Schematizzazione per l’analisi del comportamento meccanico di una struttura a nido d’ape

Si consideri una cella esagonale, come in genere vengono realizzate le strutture a nido d’ape, si è indicato le varie grandezze geometriche nel modo seguente:

l : lunghezza dello spigolo inclinato h: lunghezza dello spigolo verticale L: profondità della cella

t : spessore di parete

θ : angolo d’inclinazione della cella formato dallo spigolo l e lo spigolo h

Le caratteristiche costitutive del solido cellulare sono legate alla geometria della cella, in particolare con l diverso da h, una struttura a nido d’ape con cella esagonale, presenta un comportamento costitutivo macroscopico ortotropo. Se invece l ha la stessa lunghezza dello spigolo h, allora la cella ha la geometria di un esagono regolare e quindi il comportamento costitutivo macroscopico sarà quello di un materiale isotropo.

Il coefficiente di Poisson del solido cellulare risulta dipendente dall’angolo θ, in particolare se se θ < 0, il coefficiente risulta essere negativo, e questa è una caratteristica desiderabile, quando le schiume vengono utilizzate come materiale antiurto, ad esempio nei sistemi d’imballaggio.

Una volta definita la struttura geometrica della cella, risulta determinata immediatamente anche la densità relativa del materiale, che è espressa dalla (4.3)

      +       + = θ ϑ ρ ρ sen l h l h l t cos 2 2 * s

(4.3 – Densità relativa di una struttura a nido d’ape)

Comportamento meccanico “ in plane”

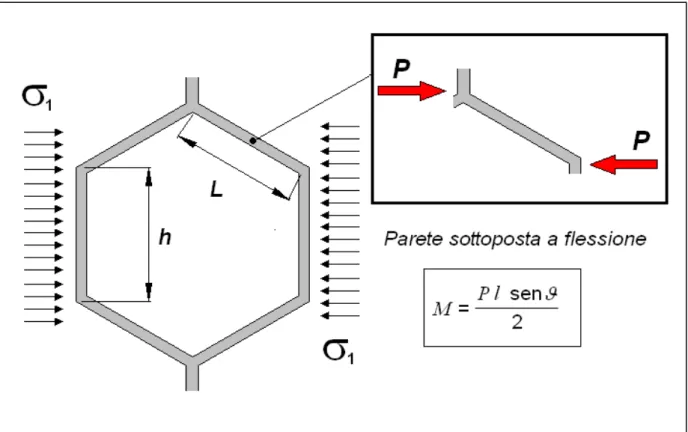
Nel caso di uno stato di sollecitazione di tipo “in plane”, la deformazione della cella è governata dalla flessione dello spigolo inclinato della cella. Quindi se si vuole avere una valutazione della rigidezza della cella nelle direzioni di carico “in plane” è sufficiente isolare lo spigolo inclinato ed andare a studiare l’equilibrio meccanico su di esso. Le figure successive 4.6, 4.7 schematizzano il problema per la valutazione della rigidezza della cella per uno stato di sollecitazione uniassiale nelle direzioni X1, X2:

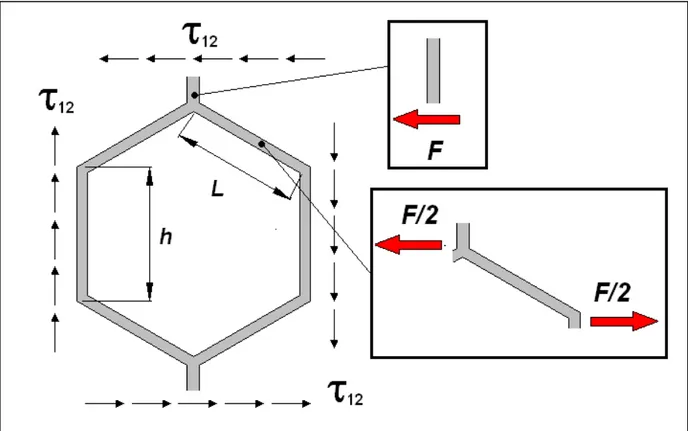
Figura 4.8 – Analisi di uno stato di tensione di taglio puro di una cella a nido d’ape

In [1] si fa l’ipotesi di poter applicare allo spigolo inflesso, la teoria della travi, infatti studiando lo spigolo della cella come una trave sollecitata a flessione è possibile ottenere le rigidezze della cella nelle direzioni 1 e 2 e quindi le espressioni dei moduli di elasticità normale e tangenziale e del coefficiente di Poisson “in plane”.

Il modulo di elasticità normale in direzione X1 è dato dal rapporto tra la tensione e la

deformazione statica della trave inflessa, che sono grandezze note dalla schematizzazione in figura 4.6. Per il modulo in direzione X2 si procede in maniera del tutto analoga.

La figura 4.8 riporta la schematizzazione utilizzata in [1], per la determinazione del modulo di elasticità tangenziale. In questo caso, mantenendo l’ipotesi di poter impiegare la teoria delle travi, anziché usare la deformazione dovuta alla flessione della parete, si utilizza la deformazione dovuta al taglio indicata in figura 4.8, e successivamente si usa la stessa procedura utilizzata per i moduli di elasticità normale.

La tabella 4.3, riporta le espressioni dei moduli per una struttura a nido d’ape con celle esagonali.

Modulo di elasticità normale in direzione X1

θ θ θ 2 3 * 1 cos sen sen L h L t Es E       +       =

Modulo di elasticità normale in direzione X2

θ θ 3 3 * 2 cos       +       = sen L h L t Es E Coefficiente di Possion θ θ θ ν sen sen L h       + = 2 * 12 cos

Modulo di elasticità tangenziale

θ θ cos 2 1 2 3 * 12       +             +       = L h L h sen L h L t Es G

Tabella 4.3 – Moduli elastici “In plane” di una struttura a nido d’ape

Poiché il materiale è ortotropo vale la relazione (4.4); se h = l , il comportamento costitutivo risulta isotropo. * 12 * 2 * 21 * 1ν Eν E = (4.4)

Per quanto riguarda la determinazione della resistenza della cella, questa risulta strettamente legata alla natura costitutiva del solido di partenza come espresso dalla tabella.

Se abbiamo a che fare con un materiale elasto-plastico, sollecitato a trazione la cella raggiungerà il collasso plastico, quando la sezione della parete soggetta a flessione raggiungerà il valore limite corrispondente al momento di completa plasticizzazione della sezione (formazione della cerniera plastica – plastic hinge). Il momento massimo sopportabile dallo spigolo sollecitato a flessione nella direzione 1 (figura 4.6), è espresso dalla (4.5):

(

)

L,t,b : dimensioni dello spigolo sollecitato a flessione

σ2: tensione normale lungo la direzione X2 τ12: tensione tangenziale

σys: tensione di snervamento del solido di partenza

Dalla relazione 4.5 è facile determinare il valore delle tensioni massime ammissibili dal materiale lungo la direzione X1:

ϑ ϑ σ σ sen sen L h L t ys pl       +       = 2 1 ) ( 2 1 *

(4.6 – Tensione ammissibile lungo X1)

Analogamente per quanto riguarda la direzione X2 , tenendo presente la figura 4.7:

2 2 2 2 2 4 1 cos 2 1 max) (M = σ bL ϑ=Mp= σ_ysbt (4.7) ϑ σ σ 2 2 2 * cos 2 1 ) (       = L t ys

pl _{(4.8 – Tensione ammissibile lungo X}

2)

Per quanto riguarda la resistenza a taglio del materiale, il momento agente sulla parete inflessa è F h/2. 2 12 4 1 cos 2 2 max F h bL Mp bt M = = τ ϑ = = σ_ys (4.9) ϑ σ τ cos 1 4 1 ) ( 2 12 * L h L t ys pl      

= (4.10 – Tensione di taglio ammissibile)

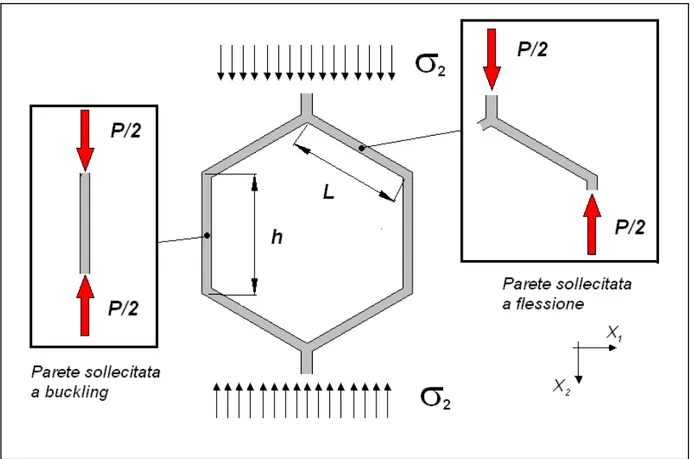
Quando la cella esagonale è sollecitata a compressione lungo direzione X2, (figura 4.6) bisogna

tenere in considerazione il possibile manifestarsi di un’instabilità di tipo euleriano sulla parete verticale della struttura. Lo schema in figura (4.9) descrive questa situazione:

Figura 4.9 – Schema di analisi per la valutazione della resistenza di una cella esagonale sottoposta a compressione nella direzione X2

Quando il carico P, che è il carico puramente assiale sopportato dalla colonna è uguale al carico critico, l’espressione di P risulta considerando una colonna di spessore t

2 2 2 2 cos 2 h EsI n Lb P= σ ϑ = π (4.11) ϑ π σ cos 1 24 ) ( 2 3 2 2 2 * lh t n Es

el _{= (4.12 – Carico critico della cella esagonale)}

Anche in questo caso la modalità di rottura dipende dalla geometria della cella, infatti se la cella è caratterizzata da un elevato t/L il buckling può precedere il collasso plastico, questo avviene se è verificata la condizione (4.13):

Es L h n L t σ_YS ϑ π 2 2 2 _cos 12       > (4.13)

Se la natura costitutiva del solido di partenza è fragile, la cella si rompe in maniera fragile, una volta che il suo spigolo sollecitato a flessione raggiunge il valore della tensione di rottura del materiale di partenza, σfs definito in [1] “modulus of ropture”.

La sezione si rompe quando il momento è tale da raggiungere tale valore, (espressione 4.14):

2 6 1

bt

Mf = σ_fs (4.14)

I corrispondenti valori limite delle tensioni:

ϑ ϑ σ σ sen sen L h L t fs cr       +       = 3 1 ) ( * ₁ 2

(4.15 – Tensione di rottura del materiale)

ϑ σ σ 2 2 2 * cos 3 1 ) (       = L t fs cr _(4.16)

Per quanto riguarda il comportamento a trazione, bisogna tener presente che quando avviene la rottura di una cella, il carico si ripartisce sulle celle restanti e bisogna quindi valutare se ci sono le condizioni per la propagazione della frattura. Un meccanismo di questo tipo richiede considerazioni di meccanica della frattura, in pratica bisogna definire un K*IC delle strutture a

nido d’ape. Per ottenere le equazioni costitutive (4.17) del materiale sottoposto ad uno stato di tensione biassiale basta combinare insieme le equazioni ottenute precedentemente nel caso di tensione monoassiale:

(

)

(

)

(

)

Lo stato di tensione biassiale influenza il comportamento a buckling della cella, il problema teorico rimane irrisolto [1]. Nel caso di un struttura a celle esagonali regolari, tutte aventi lo stesso orientamento, il buckling è possibile solo nella direzione X2 .

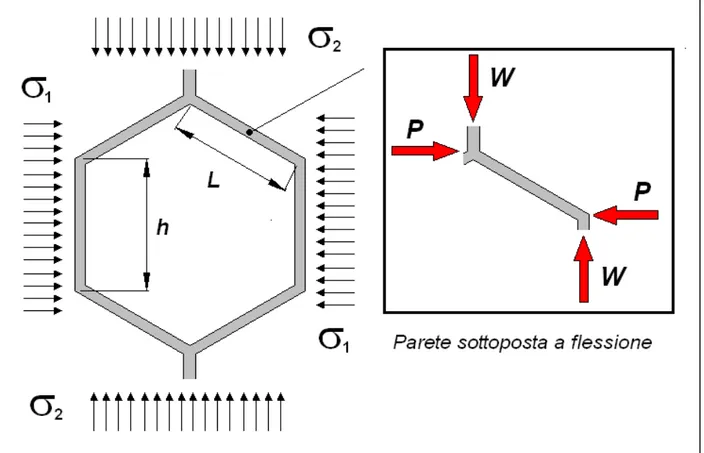
Figura 4.10 – Cella esagonale sottoposta ad uno di tensione biassiale

Si consideri lo spigolo inclinato della cella (figura 4.10 ), alle tensioni generate dalla flessione bisogna aggiungere quelle dirette assialmente. Le relazioni (4.18) riportano le espressioni del momento flettente e dello tensione assiale agente sullo spigolo.

+ + = + ± = ϑ ϑ σ θ ϑ σ σ ϑ σ θ ϑ σ cos cos 1 cos 2 1 2 1 2 2 2 1 sen sen L h t b L BLsen sen L h M a (4.18)

                − = 2 2 ₁ 4 1 ys a ysbt Mp σ σ

σ (4.19 - Momento di completa plasticizzazione della sezione)

Eguagliando il momento flettente al momento necessario per raggiungere la completa plasticizzazione si ottiene una curva che in diagramma σ1, σ2 rappresenta l’insieme di tutti gli

stati di tensioni che inducono il materiale allo snervamento (4.20):

                                +       + − =             ₋       + ± 2 2 1 2 2 2 2 1 cos cos 1 2 1 cos L t sen sen L h L t b L bLsen sen L h ys ys σ ϑ ϑ σ θ ϑ σ σ ϑ σ θ ϑ σ

(4.20) – Curva di snervamento della struttura a celle esagonali

Se invece il materiale ha una natura costitutiva fragile, raggiunge la frattura quando il momento assume il valore tale da raggiungere la tensione di rottura del materiale. Analogamente si ottiene una curva di rottura data dall’equazione (4.21)

                              +       + − =             −       + ± L t sen sen L h L t b L bLsen sen L h fs fs σ ϑ ϑ σ θ ϑ σ σ ϑ σ θ ϑ σ cos cos 1 3 1 cos _{1 2} 2 2 2 2 1

(4.21) – Curva di rottura fragile della struttura a celle esagonali

Comportamento meccanico “ out plane”

Per caratterizzare il comportamento elastico bisogna introdurre ulteriori costanti elastiche:

l t sen l h l h Es E_s       +       + = = θ ϑ ρ ρ cos 2 2 * s * (4.22)

s ν ν ν = * = 32 * 31 (4.23) 0 * 23 * 13=ν ≈ ν (4.24)

La valutazione dei moduli di taglio è molto complessa, sono state ricavate delle relazioni partendo da considerazioni energetiche:

      +       = ϑ θ sen L h L t Gs G* cos 13 _(4.25) θ ϑ ϑ ϑ ϑ cos 2 2 1 cos 2 1 2 * 23       +       +       < <             +       + sen L h sen L h L t Gs G L t L h sen L h (4.26)

Per quanto riguarda la resistenza della cella “out plane”, le modalità di rottura risultano sempre strettamente legate alla natura costitutiva del materiale.

Se il materiale elastico, a trazione la rottura avviene una volta raggiunto il valore massimo ammissibile del materiale, senza deformazioni plastiche; a compressione invece nella maggior parte dei casi prevale il buckling della cella. Il buckling “out plane” è un fenomeno abbastanza complesso [1]. Se la natura del solido è elasto-plastica, è necessario distinguere il comportamento in trazione e in compressione. A trazione è sufficiente calcolare l’effettivo valore della sezione resistente, invece a compressione, la cella tende a piegarsi fino a formare una cerniera plastica e poi collassare a causa di un buckling di tipo plastico. Se la cella è costituita da materiale fragile, a trazione bisogna tener presente la possibile presenza di difetti ed utilizzare quindi metodologie legate alla meccanica della frattura. In compressione, la struttura è decisamente più resistente che in trazione, (in presenza di difetti), tuttavia per tener conto di effetti di intaglio che si generano durante la deformazione, si utilizza una relazione semi-empirica.

La tabella 4.4, riporta le espressioni proposte da [1], per la valutazione della resistenza “out plane”.

Modello Costitutivo

Trazione Compressione

Elastico Rottura senza deformazione plastica ϑ ϑ ν σ sen sen L h h L L t Es _s el       +       + −       = 2 2 1 2 ) ( 2 3 3 * Elasto-Plastico l t sen l h l h YS pl       +       + = = θ ϑ ρ ρ σ σ cos 2 2 * ) ( s 3 * 2 3 * cos 2 4 ) (             +       + = l t sen l h l h YS pl θ ϑ π σ σ Fragile l t sen l h l h fs f       +       + = = θ ϑ ρ ρ σ σ cos 2 2 * ) ( s 3 * l t fs cr) ₁₂ ( * ₃ ≈ σ σ

Tabella 4.4 – Valori massimi ammissibili per la valutazione della resistenza “out plane” di una struttura a nido d’ape con celle esagonali

4.6 Comportamento meccanico delle schiume

La metodologia utilizzata in [1] per affrontare il problema di caratterizzare il comportamento meccanico delle schiume consiste nel trovare un modello semplice che permetta di descrivere il comportamento della schiuma, confrontarlo con i risultati sperimentali e modificarlo per trovare la convergenza. Il modello più semplice per descrivere una schiuma a celle aperte è quello riportato in figura 4.11:

Figura 4.11 – Modello semplificato per l’analisi del comportamento meccanico di una schiuma a celle aperte.

L’utilizzo di una cella a forma cubica, implica di ipotizzare un comportamento costitutivo macroscopico di un materiale isotropo. In [1] si estende alle schiume la modellazione effettuata per le celle a nido d’ape e si ipotizza che a governare il comportamento elastico-lineare della cella sia la flessione dello spigolo. Si consideri:

F: forza trasmessa dalle altre celle che agisce sullo spigolo e ne causa la sollecitazione a flessione

La forza F risulta direttamente proporzionale al prodotto delle tensioni normali e il quadrato della lunghezza l dello spigolo [1]. Lo spostamento δ invece è proporzionale al prodotto di F per la lunghezza dello spigolo al cubo ( relazioni (4.27)).

Da queste dipendenze risulta che il modulo di elasticità della schiuma risulta direttamente proporzionale alla quantità espressa dalla (4.28).

EsI FL L L F 3 2 ∝ = ∝ δ δ ε σ (4.27) 4 L FEsI E= ∝ ε σ (4.28)

Dove I non è altro che il momento d’inerzia dello spigolo della cella. Il modello in figura 4.11, ipotizza di considerare la sezione dello spigolo come un quadrato di lato t. Quindi il modulo di elasticità risulta essere direttamente proporzionale al termine t/L elevato alla quarta, e riprendendo quanto scritto nella tabella 4.1 si può scrivere la (4.29)

2 1 * *       = s C Es E ρ ρ (4.29)

Dai dati sperimentali: C1=1

Anche se consideriamo una sollecitazione di taglio puro, gli spigoli della cella tendono ad inflettersi, e con considerazioni analoghe si può scrivere:

2 2 * *       = s C Es G ρ ρ (4.30)

Dai dati sperimentali C2=3/8

3 1 1 2 1 * _{= − =} C C ν (4.31)

La tabella 4.5 riassume le espressioni del moduli di elasticità di una schiuma a celle aperte isotropa: Modulo di Young _* 2 *       = s Es E ρ ρ Modulo di Taglio _* 2 * 8 3       = s Es G ρ ρ Modulo di Poisson 3 1 * ₌ ν

Tabella 4.5 – Moduli di elasticità di una schiuma a celle aperte isotropa

Per la modellazione del comportamento meccanico di una schiuma a celle chiuse, in [1] viene proposto di utilizzare il modello riportato in figura 4.12. Se la schiuma è ricavata da un liquido, la maggior parte del materiale rimane addensato negli spigoli e quindi è approssimabile ad una schiuma a celle aperte.

Figura 4.12 – Modello semplificato per l’analisi del comportamento meccanico di una schiuma a celle chiuse.

In generale bisogna considerare alcune significative differenze, ed aggiungere dei termini correttivi.

1. La massa non si ripartisce in maniera uniforme, ma tende a concentrarsi maggiormente negli spigoli rispetto alle pareti. Bisogna quindi introdurre il fattore φ, che è stato introdotto nella caratterizzazione della topologia della cella

2. La presenza del fluido che rimane intrappolato all’interno della cella contribuisce alla rigidezza in compressione della cella. Il suo contributo è determinabile applicando la legge di Boyle (4.32):

(

)

3. Il contributo della sollecitazione membranale delle pareti della cella non è un effetto trascurabile. Alla flessione dello spigolo della cella corrisponde uno stretching della parete e contribuisce all’aumento di rigidezza a flessione.

Il contributo viene calcolato andando a scrivere l’energia elastica immagazzinata nella cella per effetto della forza F e della freccia δ, e si può scrivere secondo la (4.33):

s C ρ ρ φ) * 1 ( ' 1 − (4.33)

La tabella 4.6 riassume le espressioni del moduli di elasticità di una schiuma a celle chiuse isotropa: Modulo di Young

(

)

Per quanto riguarda la trattazione della resistenza delle schiume, tutto le considerazione fatte per descrivere il comportamento delle strutture a nido d’ape, continua a valere anche per le strutture cellulari tridimensionali. Anche nel calcolo dei valori massimi ammissibili delle tensioni sono stati determinate delle relazioni che permettano di legare questi valori alla densità relativa del materiale. Se la densità relativa è elevata, (maggiore del 0,2 – 0.3) bisogna considerare dei termini correttivi. Le tabelle 4.7 – 4.8, riportano le espressioni proposte in [1] per la valutazione della resistenza della cella aperta o chiusa.

Densità Relativa > 0.3 Buckling _* 2 * 05 . 0 _      = s el Es ρ ρ σ _* 2 1/2 2 * 1 * 03 . 0               +       = s s el Es ρ ρ ρ ρ σ Collasso Plastico _* 3/2 * 3 . 0 _      = s ys pl ρ ρ σ σ _{3/2 1/2} 2 * _* 1 * 23 . 0               +       = s s el Es ρ ρ ρ ρ σ Frattura Fragile _* 3/2 * 65 . 0 _      = s fs cr ρ ρ σ σ _* 3/2 1/2 2 * 1 * 65 . 0               +       = s s fs cr ρ ρ ρ ρ σ σ

Tabella 4.7 – Valori delle tensioni massime ammissibili di una schiuma a celle aperte

Buckling Es P P Es atm o s el ₊ −       = 2 * _* 05 . 0 ρ ρ σ Collasso Plastico ys atm o s s ys pl P P σ ρ ρ φ ρ ρ σ σ _{+ − +} −       =0.3 * (1 ) * 2 / 3 * Frattura Fragile s s fs cr ρ ρ φ ρ ρ σ σ * ) 1 ( * 65 . 0 2 / 3 * − +       =

Tabella 4.8 – Valori delle tensioni massime ammissibili di una schiuma a celle chiuse nel caso in cui la densità relativa è maggiore di 0.3, si deve aggiungere il solito termine

Con considerazioni simili a quanto fatto nella trattazione delle strutture a nido d’ape, mantenendo quindi l’ipotesi che anche il comportamento meccanico delle schiume sia condizionato dalla flessione della parete della cella, in [1] si arriva a definire anche per le schiume a celle aperte all’equazione delle superfici di snervamento (4.34) e di rottura fragile (4.35) del materiale 1 3 0 3 0 2 2 3 =                         +         ys s * m ys / s * d . . σ ρ ρ σ σ ρ ρ σ (4.34) 1 65 . 0 * 2 / 3 * + = fs s m fs s d σ ρ ρ σ σ ρ ρ σ (4.35)

Le schiume sintattiche vengono classificate come schiume a celle chiuse. L’estensione della teoria dei solidi cellulari, vista in precedenza risulta molto complessa. In [8] vengono effettuate considerazioni di tipo qualitativo per descrivere le affinità del comportamento meccanico delle schiume sintattiche con i solidi cellulari, ma l’approccio utilizzato non è di tipo analitico, ma numerico, tramite la modellazione con il metodo degli elementi finiti. Il modello di Gibson per il comportamento elastico delle schiume sintattiche è riportato al capitolo 6.