6 MODELLO STAZIONARIO DELL’IMPIANTO

6

MODELLO STAZIONARIO DELL’IMPIANTO

6.1

Introduzione

Come parte conclusiva del presente lavoro di tesi si è studiato e messo a punto un modello dell’impianto completo, con lo scopo di avere una stima, seppur grossolana, delle prestazioni dello stesso in regime stazionario e di mettere in luce il ruolo dei singoli parametri. In particolar modo l’attenzione è stata rivolta al dimensionamento dell’impianto di raffreddamento ad acqua e degli scambiatori di calore, necessari sia per mantenere la temperatura delle pareti del diffusore a valori accettabili, e sia per raffreddare il flusso prima di inviarlo alle pompe.

6.2

Configurazione dell’impianto

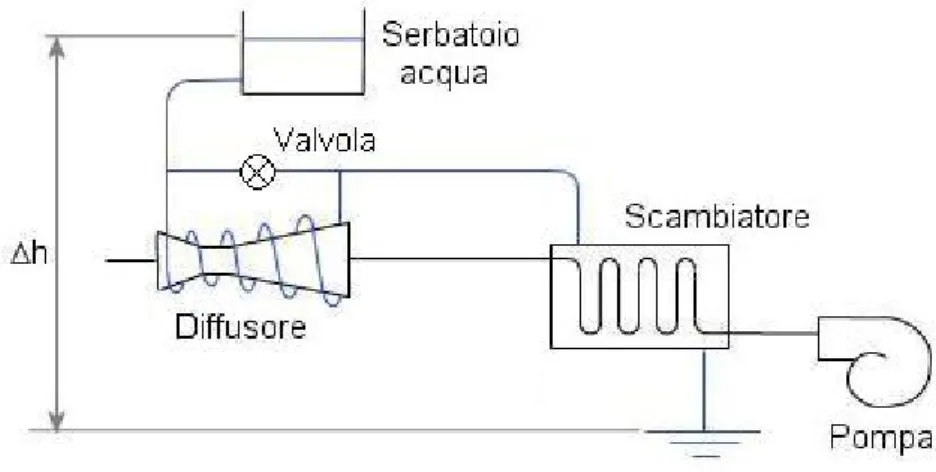
La configurazione di riferimento dell’impianto a valle dell’ugello è quella mostrata in Figura 6.1.

Il flusso in entrata viene compresso per mezzo del diffusore e successivamente inviato allo scambiatore attraverso un condotto in materiale refrattario. Nello scambiatore il gas perde gran parte della sua entalpia, mentre recupera densità per effetto dello scambio termico. Maggiore è la densità alla quale si riesce a portare il gas e minore sarà la portata volumetrica richiesta per l’impianto di pompaggio. Per incrementare la densità del gas in uscita, però, sarà necessario abbassare il più possibile la sua temperatura e questo può richiedere l’impiego di uno scambiatore eccessivamente grande. Un buon dimensionamento dell’impianto dovrà perciò tener conto di entrambi questi aspetti.

6.3

Modello del circuito di raffreddamento

I compiti principali del sistema di raffreddamento sono quelli di limitare la temperatura delle pareti del diffusore e sottrarre calore al gas prima di inviarlo alle pompe. La seconda funzione, oltre a prevenire un eccessivo riscaldamento delle pompe stesse, permette anche di recuperare densità nel gas in modo da mas-simizzare la portata di massa asportata dal sistema di pompaggio.

Il circuito di raffreddamento utilizza come fluido l’acqua attinta dal pozzo e pompata all’interno di un serbatoio ad una pressione di 3 bar. L’acqua in uscita dal circuito verrà poi nuovamente scaricata nel pozzo. Nel modello di calcolo adottato, il pozzo sarà trattato come un serbatoio di capacità termica infinita.

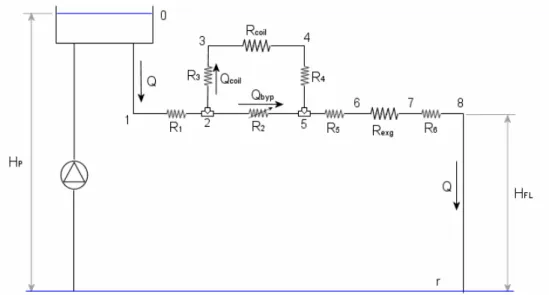
In Figura 6.2 è mostrato lo schema idraulico del circuito di raffreddamento

dove r corrisponde alle condizioni del fluido nel pozzo e 0 a quelle nel serbatoio in pressione. Con HP si è indicata la prevalenza della pompa e con Q la portata

volumetrica, che nel punto 2 si divide in due parti, quella che va ad interessare il diffusore è denominata Qcoil, l’altra è detta di bypass Qbyp. Le Ri rappresentano le

resistenze idrauliche dei tratti di condotto corrispondenti, mentre Rcoil e Rexg sono

rispettivamente la resistenza idraulica dell’avvolgimento elicoidale e quella dello scambiatore di calore. La resistenza R2 può essere variata per mezzo di una

valvola in modo da ottenere il corretto valore di Qcoil. Inoltre si dovrà tener conto

delle perdite concentrate nelle giunzioni in corrispondenza dei punti 2 e 5.

Il problema di figura può essere risolto mediante il metodo dell’analogia tra circuiti idraulici e circuiti elettrici ([1],[2],[3]), che sarà oggetto del prossimo paragrafo. Nella soluzione del problema si sono supposte valide le seguenti assunzioni:

• fluido di raffreddamento incomprimibile. Questa ipotesi pone di fatto un limite alla massima temperatura raggiungibile nell’acqua, che dovrà mantenersi suf-ficientemente al di sotto di quella di ebollizione per evitare la formazione di bolle di vapore.

• circuito di raffreddamento piano, posto ad un altezza HFL dal pelo libero

dell’acqua nel pozzo che si suppone costante. In questo modo, l’unica variazione di quota che viene considerata è quella iniziale, necessaria per portare l’acqua fino alla quota del circuito stesso.

6.3.1 Analogia tra circuiti elettrici e idraulici

Si consideri il moto stazionario di un fluido ideale incomprimibile all’interno di un condotto a sezione costante. Per il teorema di Bernoulli si avrà che su ogni linea di corrente la quantità H

′

detta carico totale si mantiene costante, ovvero

0 H s ′= ∂ ∂ (6.1)

dove con s si è indicato l’ascissa curvilinea lungo la linea d’asse del tubo. Il carico totale H

′

ha le dimensioni di una lunghezza ed è dato da

g 2 v h

H′= + 2 (6.2)

dove g è l’accelerazione di gravità. Il termine v2_{/2g della (6.2) è detto altezza}

cinetica, mentre h prende il nome di quota piezometrica ed è data da p

nella quale z rappresenta la quota geodetica, mentre p/ρg è l’altezza piezometrica dovuta alla pressione.

Se le linee di corrente sono tutte rettilinee e parallele, ovvero si è in presenza di una corrente gradualmente variata, si può dimostrare che la quota piezometrica h è uniforme su ogni sezione del condotto. In generale v può non essere uniforme nella sezione variando da una linea di corrente all’altra, così come farà anche il carico totale H

′

. Per definire un carico totale H medio, relativo all’intera sezione, è quindi necessario introdurre la velocità media U, data dal rapporto tra la portata volumetrica e l’area della sezione del condotto

A Q

U=

che, per le ipotesi di fluido incomprimibile e sezione del tubo costante, risulta uguale in tutte le sezioni del condotto.

A questo punto H può essere definito imponendo la condizione che la potenza del flusso sia costante lungo il condotto

0 dA gHU s _A ⎟⎟_⎠= ⎞ ⎜ ⎜ ⎝ ⎛ ρ ∂ ∂

∫

(6.4) ottenendo α + = g 2 U h H 2 (6.5) dove α=

∫

A 3 3_A v dA U

1 _{prende il nome di coefficiente di Coriolis ed è sempre} maggiore di 1. Poiché nei casi di interesse pratico α=1.06÷1.08, per calcoli di prima approssimazione è possibile porre α=1. Per il carico totale definito dalla (6.5) è possibile scrivere un’equazione formalmente identica alla (6.1), ma valida per l’intero tubo anziché per una singola linea di corrente.

Nel caso di fluido reale, l’equazione di Bernoulli deve essere modificata per tener conto delle perdite per attrito, ovvero

J g 2 U h s H s 2 − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ = ∂ ∂ (6.6)

dove J è un termine sempre positivo detto cadente. In base alla formula di resistenza di Darcy-Weisbach il cadente può essere espresso tramite la relazione

D 1 U g 2 1 J_{= f} 2 _(6.7)

dove D è il diametro del condotto e f è il fattore di attrito. Nel paragrafo successivo saranno brevemente riassunte le principali formule comunemente impiegate per il calcolo di f.

Integrando la (6.6) tra due sezioni 1 e 2 a distanza L si ottiene

D L U g 2 1 ds J H H 2 L 2 1− =

∫

= f (6.8)

Moltiplicando ambo i membri della (6.8) per ρg e facendo comparire al secondo membro la portata volumetrica al posto della velocità si ottiene la seguente espressione per le perdite di pressione nel condotto

2 5 2 loss Q D L 8 z g p f π ρ + ∆ ρ = ∆ (6.9)

se si considera un tratto di condotto piano la (6.9) può essere riscritta come

2 loss RQ p = ∆ (6.10) dove la quantità _{2 5} f D L 8 R π ρ

= prende il nome di resistenza idraulica in analogia con la legge di Ohm per i conduttori elettrici. E’ facile dimostrare che, per le resistenze idrauliche, valgono le seguenti leggi di composizione:

• resistenze in serie 2 eq loss R Q p = ∆ con R_eq =R₁+R₂ • resistenze in parallelo 2 eq loss R Q p = ∆ con 2 1 eq R 1 R 1 R 1 _{= +}

sono disponibili in letteratura i fattori di perdita k relativi ad un’ampia gamma di casi, con k dato dal rapporto tra la caduta di pressione causata dalla perdita concentrata e la pressione dinamica del flusso in ingresso o in uscita.

2 loss U 2 1 p k ρ ∆ = (6.11)

Dalla (6.11) è poi immediato calcolare la resistenza idraulica corrispondente alla perdita concentrata 4 2_D k 8 R π ρ = (6.12)

dove Din è il diametro del tubo al quale si riferisce la U.

Dato un circuito idraulico, alimentato da una pompa con prevalenza HP, è

possibile ridurlo mediante scomposizione in serie e paralleli ad un circuito con un’unica resistenza equivalente. Imponendo poi la condizione

( )

2 eq loss P Q p R Q H g =∆ = ρ (6.13) sarà possibile determinare la portata volumetrica all’interno del circuito, in corrispondenza dell’intersezione tra la curva di carico e la curva caratteristica della pompa.

6.3.2 Determinazione del fattore di attrito

In regime laminare, convenzionalmente associato a ReD < 2100, il fattore di

attrito può essere valutato mediante la nota relazione

D

Re 64 =

f (6.14)

valida indipendentemente dalla rugosità della superficie interna del tubo.

In regime turbolento, al contrario, la finitura superficiale del tubo assume una notevole rilevanza. Per tubi idraulicamente lisci1_{, f obbedisce alla classica legge di}

Karman-Nikuradse

1 _{un tubo può considerarsi idraulicamente liscio quando le asperità della sua}

(

f

)

f 0.8 2log10ReD

1 _{=− +}

(6.15)

Per tubi scabri si definisce la rugosità relativa come il rapporto tra lo spessore medio delle asperità della superficie (indicato con ε) e il diametro del tubo.

Nel caso di flusso completamente turbolento2_{, si osserva che f risulta praticamente}

indipendente dal numero di Reynolds e può essere espresso attraverso la relazione sperimentale ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ε + =1.14 2log D 1 10 f (6.16)

per regimi turbolenti non completamente sviluppati, invece sarà necessario far ricorso a diagrammi come quello di Moody (Figura 6.3)

Figura 6.3 Diagramma di Moody ([4]).

2 _{il flusso è considerato completamente turbolento quando si verifica la condizione}

6.3.3 Determinazione delle resistenze idrauliche e soluzione del circuito

A questo stadio del progetto non è ancora possibile conoscere con esattezza le lunghezze dei vari tratti del circuito e sarà perciò necessario fare delle ipotesi cercando di essere per quanto possibile cautelativi. I valori di lunghezze e diametri considerati per i vari tratti di Figura 6.2 del condotto sono riportati nella seguente Tabella 6.1 Tratto Lunghezza [m] Diametro [mm] 1-2 15 35 2-3 1.5 9 4-5 1.5 9 2-5 1 35 5-6 2 35 7-8 15 35

Tabella 6.1 Parametri geometrici del circuito.

Per quanto concerne, invece, la quota geodetica del circuito HFL, essa è stata

stimata in 6 metri.

Le perdite concentrate in corrispondenza delle giunzioni 2 e 5 sono state valutate in base al fattore di perdita k. Nella seguente Figura 6.4 sono riportati alcuni valori di k, relativi a giunzioni a T e raccordate.

Sfruttando le formule di composizione delle resistenze idrauliche è possibile ridurre l’intero circuito ad un’unica resistenza equivalente Req data da

6 exg 5 2 4 coil 3 2 1 eq R R R R R R 1 R 1 R R _⎟⎟ + + + ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + + + + = − (6.17)

dove R1 e R5 sono soprassegnate per indicare che in esse sono stati inclusi anche i

contributi delle perdite concentrate rispettivamente in 2 e 5.

Una volta calcolata la resistenza equivalente con la (6.17) è possibile determinare la prevalenza HP della pompa, in funzione della portata che si vuole

mantenere nel circuito.

( )

eq

( )

2 FL P _g Q Q R H Q H ⋅ ρ + = (6.18)

6.4

Modello del diffusore raffreddato

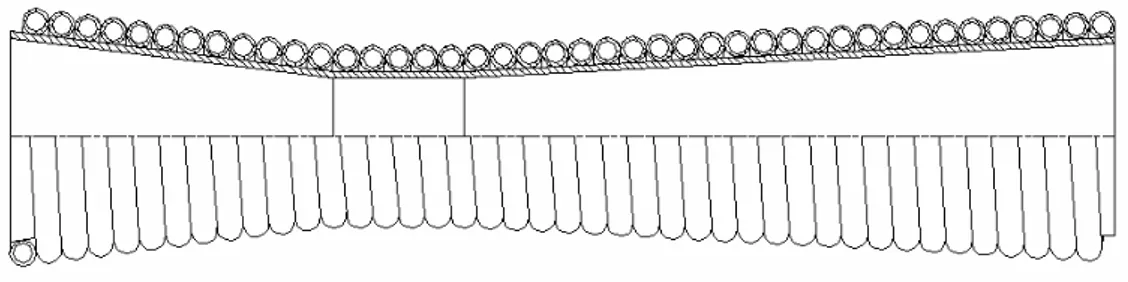
Come detto precedentemente, il diffusore dovrà essere dotato di un sistema di raffreddamento delle pareti che consenta di mantenere la temperatura ad un livello accettabile per il materiale impiegato. La soluzione prescelta per il raffreddamento è stata quella di un avvolgimento elicoidale, saldato sulla parete esterna del diffusore, all’interno del quale scorre l’acqua di raffreddamento (Figura 6.5). Poiché il diffusore è destinato ad operare all’interno della camera a vuoto, ad una pressione dell’ordine di qualche decina di Pascal, è ragionevole trascurare lo scambio termico con l’aria circostante e considerare solo quello tra il gas all’interno e il liquido refrigerante.

Si farà inoltre l’ipotesi che tutte le parti solide che compongono il diffusore siano alla stessa temperatura Tw. Se Q& è la potenza termica complessivamente

scambiata nel diffusore allora vale la relazione ([5],[6])

(

)

∫

− = coil S L w L T T dS h Q& (6.19)

dove Scoil è la superficie interna dell’avvolgimento elicoidale e hL e TL sono

rispettivamente, i valori locali di coefficiente di scambio termico convettivo e temperatura del fluido refrigerante. Poiché Tw è costante dalla (6.19) si ottiene

∫

∫

+ = coil coil S L S L L w dS h dS T h Q T & (6.20)

che permette di determinare il valore della temperatura delle pareti, una volta che Q& , hL e TL siano stati calcolati con gli appositi modelli descritti nei paragrafi

successivi. Essendo le quantità a destra della (6.20), esse stesse funzioni della temperatura Tw, la soluzione del problema dovrà essere ottenuta iterativamente.

Il problema è stato affrontato suddividendo il diffusore in tre parti, tratto convergente gola e tratto divergente. Per il tratto convergente sono stati sfruttati i risultati ottenuti per via numerica nel capitolo precedente, dove si era ottenuta una relazione funzionale tra il calore scambiato e la temperatura della parete. Per gola e tratto divergente è stata invece utilizzata la teoria unidimensionale illustrata in appendice A, valida per condotti conici e che tiene conto di attrito e scambio termico.

Figura 6.5 Disegno CAD di una possibile configurazione del diffusore raffreddato mediante avvolgimento elicoidale percorso da acqua.

6.4.1 Tratto convergente del diffusore

Supponendo di conoscere il valore di Tw ad un generico passo dell’iterazione, la

potenza termica Q&conv scambiata tra gas caldo e refrigerante nel tratto

convergente può essere ricavata dalle simulazioni numeriche fatte nel capitolo precedente. In particolare sostituendo la (5.12) nella (5.11) si ottiene

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + θ + − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = − − 3 1 i 2 i 3 01 w 01 p 01 02 01 p conv D D 10 x 78 . 0 0063 . 0 T T 0824 . 0 123 . 0 T c m T T 1 T c m Q & & & (6.21)

nella quale i parametri θ e Di2/Di1 si considerano noti.

Una volta noto Q&_conv, la temperatura di uscita del refrigerante TLout può essere

determinata imponendo il bilancio energetico ([5],[6])

( )

L

(

Lout Lin

)

L L

conv m C T T T

Q& = & − _(6.22) dove m&_L e TLin sono rispettivamente il flusso di massa e la temperatura di

ingresso del liquido, che si considerano assegnati; mentre CL

( )

TL è il suo calore

specifico, valutato alla temperatura media nel tratto di condotto considerato. In prima approssimazione si può adottare per C_L un valore costante riferito ad una temperatura plausibile. In alternativa si può utilizzare una delle molte relazioni empiriche disponibili in letteratura; in questo caso, però, dato che TL dipende da

TLout e la (6.22) non risulterà invertibile e sarà necessario risolvere tale equazione

6.4.2 Tratto divergente del diffusore

Il modello di calcolo della parte divergente del diffusore è basato sulla scomposizione del condotto in una serie di tratti cilindrici, ognuno dei quali è circondato da un elemento toroidale all’interno del quale scorre il fluido refrigerante. Se Nd è il numero complessivo di spire dell’avvolgimento elicoidale

del divergente, la scomposizione è fatta suddividendo il condotto in altrettanti elementi di lunghezza pari al diametro esterno de del tubo.

Figura 6.6 Modello teorico del generico elemento i-esimo del tratto divergente. Si noti che questo tipo di trasformazione non conserva la lunghezza del condotto stesso, infatti la sua lunghezza reale sarà data da N_dd_ecosθ_d, mentre nel modello trasformato la lunghezza complessiva risulta N_dd_e. Tuttavia l’errore può ritenersi trascurabile poiché per il divergente si prevedono angoli di semiapertura θd molto piccoli (inferiori a 3°).

Come detto ogni tratto troncoconico del condotto sarà approssimato con un cilindro, il cui diametro interno D_eq sarà tale da far in modo che la superficie interna sia conservata, ovvero

D cos D D d eq = _θ ≅

dove D è il diametro medio geometrico del tratto di condotto considerato.

Imponendo il bilancio energetico per il generico elemento i-esimo, rappresentato in Figura 6.6, è possibile ricavare l’incremento di temperatura del fluido ∆TL,i relativo alla spira.

( )

Li, Li, i, L L i, div m C T T Q& = & ∆ _(6.23) dove, ancora una volta TL,i è la temperatura media del liquido di raffreddamento

ed è legata al ∆TL,i dalla relazione

(

L,i 1 L,i

)

1 i , L i , L ₂ T T 1 T T = ₋ + ∆ ₋ +∆ (6.24)

nella quale TL,i−1 e ∆TL,i-1 sono noti dal calcolo relativo alla spira precedente.

La potenza termica Q&divi, ceduta al refrigerante nell’i-esimo tratto del

divergen-te sarà pari a quella sottratta al gas nel medesimo tratto. Come precedendivergen-temendivergen-te accennato, per il calcolo di Q&divi, relativamente al gas, si è utilizzato il metodo

descritto in appendice A. Tale metodo è basato sulla soluzione delle equazioni del moto unidimensionale nel caso in cui siano presenti variazioni di area, attrito e scambio termico. Le ipotesi alla base del metodo sono:

• gas caloricamente perfetto.

• variazione lineare del diametro lungo l’asse del condotto.

• coefficiente di attrito cf e numero di Stanton Ch costanti nel condotto

considera-to.

• fattore di recupero unitario.

• temperatura alla parete proporzionale alla temperatura totale del flusso. Il modello unidimensionale consente di calcolare il rapporto tra le proprietà del flusso a monte e a valle di una porzione di condotto del quale si conosca il numero di Mach in entrata e quello in uscita, in funzione dei parametri cf, Ch, tanθ e Tw/T0.

Perciò applicando tale modello all’elemento i-esimo del divergente si ottiene una relazione del tipo

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = i 01 02 i, 01 p i, div _T T 1 T c m Q& & (6.25) con ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ θ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ i 0 w d i , h i , f i , 2 i , 1 i 01 02 T T , tan , C , c , M , M T T 0 T f (6.26)

dove il pedice 1 indica la sezione d’ingresso del tratto di condotto, il 2 indica l’uscita, mentre il simbolo soprasegnato fa riferimento alle condizioni medie, definite come media aritmetica tra le condizioni di ingresso e uscita. Poiché nella (6.26) si introduce un ulteriore incognita, vale a dire M2,i, è necessario imporre

un’altra condizione per rendere il problema determinato: tale condizione sarà ov-viamente quella sul rapporto delle aree del tratto i-esimo

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ θ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ i 0 w d i , h i , f i , 2 i , 1 i 1 2 T T , tan , C , c , M , M A A A f (6.27)

dove (A2/A1)i è noto e vale, nell’ipotesi di θd piccolo,

d i, 1 e i 1 2 _sin D d 2 1 A A _{≅ − θ} ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ (6.28)

Anche in questo caso, la soluzione del sistema dato da (6.23), (6.25), (6.26) e (6.27) deve essere ottenuta mediante una procedura iterativa. Il procedimento utilizzato è composto dai seguenti passi:

• si ipotizzano dei valori di Tw/T0, cf e Ch di primo tentativo, uguali per tutte le

sezioni del condotto.

• conoscendo tutti i parametri del flusso in ingresso all’i-esimo elemento si ricava per tentativi dalla (6.27) il valore M2,i che fornice il valore corretto del rapporto

delle aree dell’elemento in esame.

• una volta determinato il giusto valore di M2,i, dall’applicazione del modello

unidimensionale, è possibile calcolare i parametri del flusso all’uscita. In particolare dalla (6.26) si ottiene (T02/T01)i che sostituito nella (6.25) fornisce il

valore della potenza termica Q&_divi, scambiata tra gas e liquido nell’elemento i-esimo del divergente.

• a questo punto dalla (6.23) si ottiene, in modo analogo a quanto fatto nel paragrafo precedente, l’incremento di temperatura del liquido ∆TL,i relativo alla

spira i-esima.

nuovo valore di (Tw/T₀)i e nuovi valori di c_fi, e C_h,i basati sui valori medi, nel

tratto corrispondente, dei numeri di Prandtl e Reynolds.

• utilizzando questi nuovi valori dei parametri si effettua nuovamente lo stesso procedimento finché non si raggiunge la convergenza. Ad esempio la condizione di convergenza può essere effettuata sul massimo valore dello scarto su (Tw/T0)i

tra due iterazione successive.

6.4.3 Gola del diffusore

Assumendo che la lunghezza della gola sia pari a N_gd_e, dove Ng è il numero di

spire dell’avvolgimento elicoidale nel tratto di gola, è possibile adottare un metodo di calcolo molto simile a quello utilizzato per il divergente. In particolare, l’equazione (6.23) resta formalmente immutata, mentre nella (6.26) il termine tanθ diviene identicamente nullo poiché il tratto di gola è cilindrico. Per determinare il numero di Mach in uscita da ogni singolo tratto M2,i, invece, non è

più possibile utilizzare la (6.27), che non ha più alcun senso, ed è necessario quindi ricorrere ad un’altra condizione. Nel caso di un condotto a sezione costante, il modello unidimensionale fornisce la seguente equazione differenziale per la variazione del numero di Mach lungo l’asse3

(

)

[

]

D dx 4 M K c K M 2 1 1 M 1 1 M dM 2 h f h 2 2 2 2 − γ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ γ− + − = (6.29)

con K_h =C_h

(

1−T_w T₀

)

, che nelle solite ipotesi di Tw/T0, cf e Ch costanti può essere

integrata ottenendo

(

)

(

)

(

(

)

)

c 2 1 h f h 2 2 h f h b 2 1 2 2 a 2 1 2 2 D x M K c K M K c K M 1 2 M 1 2 M M e _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − γ + − − γ + − ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − γ + − γ + ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ∆ (6.30) dove si è posto

(

)

(

)

(

)

h f h h f h f h K 1 c 2 K K c 1 2 c K 1 c 2 1 b K 1 a + γ − γ − γ − = + γ − γ + γ = − =

Per ogni tratto della gola, conoscendo il numero di Mach in ingresso, è possibile ricavare il Mach in uscita sfruttando la (6.30) nella quale si pone ∆x=de e D uguale

al diametro interno della gola. Il resto della procedura di calcolo utilizzata per la gola rimane sostanzialmente identico a quanto fatto per il divergente.

6.4.4 Calcolo della temperatura alla parete

Come detto all’inizio del paragrafo, il calcolo del diffusore deve essere effettuato iterativamente rispetto alla temperatura della parete Tw, partendo da un valore di

primo tentativo e calcolando i nuovi valori per mezzo della (6.20). In base alla scomposizione descritta nei paragrafi precedenti la (6.20) può essere riscritta nella forma

∑

∑

∑

∑

= = = = + + + + + = d g d g N 1 i div i , L div i , L N 1 i gola i , L gola L conv i , L gola L N 1 i div i , L div i , L div i , L N 1 i gola i , L gola i , L gola L conv i , L conv i , L conv L w h S h S h S T h S T h S T h S Q T & (6.31)

dove Q& è la potenza termica complessiva ed è data da

∑

∑

= = + + = g Nd 1 i i , div N 1 i i , gola conv Q Q Q

Q& & & &

conv L

S e gola

L

S sono rispettivamente, la superficie interna dell’avvolgimento relativo al tratto convergente e a quello relativo al tratto di gola e possono essere valutati in modo approssimato mediante le relazioni

(

)

∑

= + + π = Nc 1 i e i , conv i 2 conv L d D 2t d S

(

gola e

)

g i 2 gola L d N D 2t d S =π + +

Analogamente, div 2 _i

(

_{div,i e}

)

i

,

L d D 2t d

S =π + + è la superficie interna della spira i-esima del tratto divergente.

Per quanto riguarda il calcolo del coefficiente di scambio termico convettivo

( )

L

L T

h è stato utilizzato il modello proposto da Mori e Nakayama ([7],[8]) e descritto nel paragrafo successivo.

6.4.5 Flusso all’interno di tubi curvi

Il problema del calcolo del flusso all’interno di un tubo con linea d’asse curva è sicuramente uno dei più studiati, sia teoricamente che sperimentalmente, di tutta la fluidodinamica per i suoi notevoli interessi applicativi, soprattutto nel campo dello scambio termico.

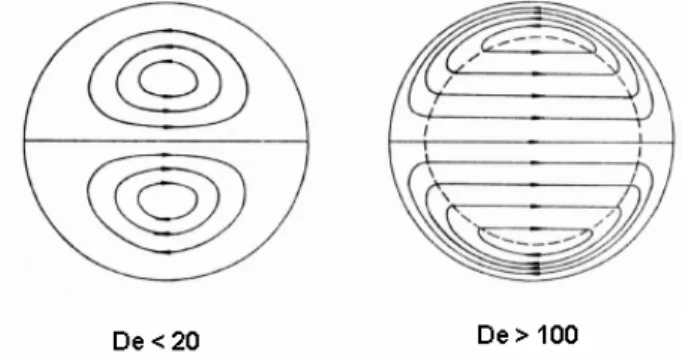
I primi lavori teorici relativi al flusso laminare incomprimibile in un condotto curvo, furono pubblicati alla fine degli anni ’20 da Dean ([9],[10]). Dean mise in luce come al campo fluidodinamico assiale, analogo a quello che caratterizza i tubi dritti, si sovrapponga un campo di velocità trasversale, alimentato dalle forze centrifughe, che tende a spostare il fluido dalla zona dell’intradosso del tubo verso l’estradosso creando così due ampie zone di ricircolo nella sezione del tubo (Figura 6.7). L’effetto della presenza del campo secondario è quello di aumentare sia l’attrito, che lo scambio termico tra il fluido e le pareti del condotto rispetto ad un tubo dritto a parità di diametro e gradiente di pressione.

Dean individua, inoltre, il parametro adimensionale che determina le proprietà del campo secondario e che, per questa ragione, nella letteratura odierna viene spesso denominato numero di Dean:

c

R r Re

De=

dove r è il raggio della sezione del condotto e Rc è il raggio di curvatura locale della

linea d’asse del tubo. Gli effetti del campo secondario sono tanto più marcati quanto più elevato è il numero di Dean. Questo fenomeno è ben illustrato in Figura 6.7, per bassi De la posizione dei nuclei vorticosi è piuttosto centrale e quindi l’interazione con le pareti è debole; esperimenti condotti da White ([11]) dimostrano che per De<11.6 gli effetti del flusso secondario sono del tutto trascurabili. All’aumentare di De la posizione dei vortici si sposta verso le pareti creando una forte interazione con le stesse; in queste condizioni il campo secondario assume un tipico aspetto a due strati, con un core flow uniforme e uno strato limite lungo le pareti del condotto dove si ha il ricircolo del fluido.

La presenza del campo secondario ha importanti conseguenze anche per quanto riguarda l’instabilità del flusso all’interno del condotto, in particolare l’effetto è quello di aumentare il Reynolds critico. A tale proposito Ito ([13]) ha determinato empiricamente la seguente formula valida per r/Rc compresi tra 1/15 e 1/860;

32 . 0 c crit _R r 20000 Re _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = (6.32)

per r/Rc minori di 1/860 il Reynolds critico coincide con quello di un tubo dritto.

Nel corso degli anni sono stati proposti numerosi modelli sia teorici che sperimentali per la stima del coefficiente di attrito e del numero di Nusselt all’interno di tubi con linea d’asse curva, sia nel caso turbolento che laminare. In questo lavoro si è fatto riferimento a quello proposto da Mori e Nakayama, che offre i vantaggi di completezza e ampiezza di applicabilità oltre ad un buon accordo con i dati sperimentali.

Il modello di Mori e Nakayama è basato sulla suddivisione del campo in core flow e strato limite e perciò è applicabile per numeri di Dean sufficientemente elevati da rendere verosimile questa assunzione. Senza entrare nei dettagli del calcolo, di seguito sono elencati i principali risultati.

Nel caso di flusso laminare, si ha ([7]):

• spessore medio dello strato limite del flusso secondario

De 631 . 4 r m ₌ δ (6.33)

valida per De>103_.

• fattore di attrito4

( )

De De 108 . 0 12 lam c f s k f f _{= ⋅} ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ (6.34) 4 _{definito come}

(

)

_d V 2 1 ds dp c 4 _{f 2} ρ − = = f

dove fc è il fattore di attrito per il tubo curvo, mentre fs è il fattore di attrito per

un tubo dritto con lo stesso numero di Reynolds e vale (fs)lam=64/Re. Il fattore

correttivo

( )

_{1 3.253De} 12 1 De ₋ − = f k (6.35)

migliora l’accuratezza della (6.34) a bassi numeri di Dean, mentre per De>103

può essere posto uguale a 1. • numero di Nusselt5

(

De, ,Pr

)

De 198 . 0 Nu Nu Nu 2 1 lam c _{⋅ ζ} ζ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ k s (6.36)

dove nuovamente il numero di Nusselt per il tubo curvo è stato espresso in rapporto a quello per il tubo dritto corrispondente pari a (Nus)lam=48/11. Il

parametro ζ è il rapporto tra lo spessore dello strato limite termico e dello strato limite di velocità ed è funzione del numero di Prandtl, secondo la relazione ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + = ζ 2 Pr 1 4 77 1 1 11 2 _(6.37)

Anche in questo caso kNu rappresenta un fattore di correzione per bassi numeri

di Dean e vale, per Pr > 1

(

)

2 1 Nu De Pr 10 1 30 13 10 1 120 17 40 1 05 . 37 1 1 Pr , , De − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ζ + ζ − ζ + = ζ k (6.38) 5 _{definito come}

(

Tw Tm

)

k d q Nu − ⋅ =

dove q è il flusso di calore, k è la conducibilità termica del fluido, Tm e Tw sono

Nel caso di flusso turbolento ([8]) si suppone che, il fattore di attrito relativo ad un tubo dritto, abbia un’espressione del tipo

( )

s turb _Re1m

1 α =

f (6.39) dove il coefficiente α è esso stesso funzione della costante m.

Per numeri di Reynolds più bassi (ovviamente sempre maggiori del Recrit) si ha

una miglior corrispondenza con i dati sperimentali per m=4, mentre m=5 funziona meglio per Re maggiori. Per tubi dritti il Reynolds di transizione tra i due valori di m è approssimativamente R ′es=50000, mentre per tubi curvi gli autori

suggeriscono il seguente criterio

⎪ ⎩ ⎪ ⎨ ⎧ > ′ < × = ′ 170 r R per e R 170 r R per R r 10 5 . 6 e R c s c c 5 c (6.40)

Per Re<R ′ec, adottando m=4, si ha per α il valore 0.305 e si ottengono le seguenti

espressioni per:

• spessore medio dello strato limite

5 2 c 5 1 4 m m r R Re 257 . 0 r ⎟⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ δ = (6.41) • fattore di attrito

( )

(

)

[

]

[

(

)

]

_⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + × = = ₂ 15 c 5 1 2 c c turb 4 m c R r Re 112 . 0 1 R r Re 300 . 0 R r f (6.42) • numero di Nusselt

(

)

₍

₎

(

)

[

]

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ × − = = ₂15 c 10 1 c 5 4 3 2 turb 4 m c R r Re 098 . 0 1 R r Re 074 . 0 Pr 2 . 26 Pr Nu (6.43)

Nel caso in cui Re>R ′e_c si ha invece m=4, α=0.184 e si ricava: • spessore medio dello strato limite

12 5 c 6 1 5 m m r R Re 190 . 0 r ⎟⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ δ = (6.44) • fattore di attrito

( )

(

)

[

]

[

(

)

]

_⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + × = = _2.5 16 c 6 1 5 . 2 c c turb 5 m c R r Re 068 . 0 1 R r Re 192 . 0 R r f (6.45) • numero di Nusselt

(

)

(

)

[

]

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ × = = _2.5 16 c 12 1 c 6 5 4 . 0 turb 4 m c R r Re 061 . 0 1 R r Re 0 . 41 Pr Nu (6.46)

6.4.6 Perdite di pressione nel liquido

In questo paragrafo verrà ricavata la resistenza idraulica dell’avvolgimento elicoidale, che sarà data dalla somma delle resistenze dei tre tratti considerati. Poiché si è supposto la densità del liquido costante si avrà:

⎥⎦ ⎤ ⎢⎣ ⎡ _{+ +} π ρ = + + =

∫

Lconv

∫

div

∫

gola

0 L 0 L 0 5 i 2 gola div conv Coil d d d d 8 R R R R l l l f f f (6.47)

dove Lconv, Ldiv e Lgola sono le lunghezze degli avvolgimenti elicoidali nei tre tratti

ed f è il valore locale del fattore di attrito calcolato con il modello di Mori e Nakayama.

Gli integrali al secondo membro della (6.47) sono stati valutati in modo approssimato. Per quanto riguarda il tratto convergente si è valutato f in base ai valori medi delle proprietà fisiche e geometriche nel tratto e lo si è supposto costante sull’intera lunghezza, in questo modo

(

)

∑

∫

conv = ≅π N₌c + + 1 i convi, e conv conv conv L 0 f dl f L f D 2t d (6.48)

Per tratto divergente e gola si è invece proceduto in maniera analoga a quanto fatto per il calcolo dello scambio termico, suddividendo l’elica in spire e supponen-do costanti le proprietà su ogni spira

(

divi, e

)

N 1 i i, div N 1 i i, div i, div L 0 d L D 2t d d d div + + π = =

∑

∑

∫

f l ₌ f ₌ f (6.49)

(

_)∑

∫

gola =π + + N₌g 1 i i, gola e gola L 0 f dl D d 2t f (6.50)

6.4.7 Coefficiente di attrito e numero di Stanton per il gas

Per quanto riguarda la determinazione del coefficiente di attrito del gas all’interno del tratto divergente e della gola del diffusore è stato utilizzato il modello proposto da Van Driest ([14]), valido per uno strato limite comprimibile, turbolento su una lastra piana. Questo modello permette di calcolare il coefficiente di attrito locale in funzione dei numeri di Mach e Reynolds locali e del rapporto tra la temperatura alla parete e quella del flusso esterno, attraverso la relazione implicita

(

)

(

)

⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + = β + α ω + 5 . 0 w f x 10 w f T T c Re log 41 . 0 sin a sin a T T c A 242 . 0 _(6.51)

nella quale ω è l’esponente della legge esponenziale per la viscosità e può essere determinato in base alla legge di Sutherland per l’intervallo di temperatura di interesse. Le quantità α e β sono date da

2 2 2 A 4 B B A 2 + − = α 2 2 _4A B B + = β dove T T M 2 1 A w 2 2 − γ = e 1 T T M 2 1 1 B w 2 − − γ + =

Poiché tra le ipotesi alla base del modello di Van Driest c’è quella di numero di Prandtl unitario, sfruttando l’analogia di Reynolds per il calcolo del numero di Stanton, si ottiene semplicemente

2 c

C f

h = (6.52)

6.5

Modello dello scambiatore

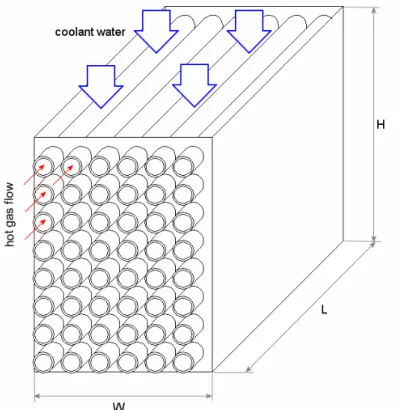
Per la stima delle prestazioni e dimensionamento preliminare dello scambiato-re di caloscambiato-re, si è fatto riferimento ad una configurazione molto semplice, come mostrato in Figura 6.8.

Figura 6.8 Schema dello scambiatore di calore a flussi incrociati.

Lo scambiatore è sostanzialmente del tipo a tubi e mantello a correnti incrocia-te, con mescolamento nel fluido del mantello. All’interno dei tubi scorre, con un singolo passaggio, il gas caldo proveniente dal diffusore. Il banco di tubi è investito

Lo scopo principale del dimensionamento sarà quello di determinare il valore della superficie di scambio termico, necessaria affinché la potenza termica richies-ta possa essere trasferirichies-ta dal gas al refrigerante. Assumendo come superficie di riferimento quella del liquido sarà

L d N

S= π _e (6.53) dove N è il numero dei tubi, de è il loro diametro esterno ed L è la loro lunghezza.

Nel modello adottato si sceglie di fissare de ed N come parametri di progetto e si

determina L in base alla superficie di scambio.

Conoscendo le temperature di ingresso del gas Tg1 e del liquido TL1, e fissando

arbitrariamente il valore della temperatura del gas che si vuol ottenere in uscita Tg2 è possibile calcolare la temperatura del liquido in uscita TL2 mediante il

bilancio energetico

(

g1 g2

)

L L

(

L2 L1

)

pg

gc T T m c T T

m

Q& = & − = & − (6.54) Seguendo il procedimento illustrato da Kreith ([5]), la potenza termica scambiata può essere posta nella forma

eff

T S U

Q& = ∆ (6.55) dove U è la conduttanza globale unitaria. Supponendo che lo spessore dei tubi t sia abbastanza piccolo rispetto al diametro, si ha per U l’espressione

L g L g h 1 h 1 h 1 k t h 1 U 1 ₊ ε ≅ + ε + ε = (6.56)

dove ε=di/de e k è la conducibilità termica del materiale dei tubi. Per i valori

normalmente in gioco in questo problema, il termine nella (6.56) dovuto al contributo della parete può essere considerato trascurabile. Per quanto riguarda ∆Teff si tratta di una differenza di temperatura effettiva data dalla media

logaritmica delle differenze di temperatura tra gas e liquido, moltiplicata per un coefficiente correttivo F che tiene conto della geometria dello scambiatore.

(

) (

)

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − − − − = ∆ 2 L 2 g 1 L 1 g 2 L 2 g 1 L 1 g eff T T T T ln T T T T F T (6.57)

Il fattore F, per la tipologia di scambiatore in esame, può essere derivato dal grafico di Figura 6.9 al variare del parametro

2 g 1 g 1 L 2 L T T T T Z − − =

Figura 6.9 Fattore di correzione F per uno scambiatore di calore a correnti incrociate con il fluido nel mantello mescolato e singolo passaggio nei tubi ([5],[6]).

I modelli di calcolo adottati per i coefficienti di scambio termico hg e hL

saran-no descritti nei prossimi paragrafi. Si anticipa comunque che, poiché hL risulta

dipendente dall’incognita del problema L, ancora una volta la soluzione dovrà essere ottenuta per via iterativa, ipotizzando un valore di primo tentativo per L e procedendo per approssimazioni successive.

6.5.1 Coefficiente di scambio termico e perdita di pressione per il liquido

Si consideri un banco di tubi investito ortogonalmente da una corrente. Per definire le proprietà fisiche del fluido è utile introdurre le seguenti temperature caratteristiche ([5]):

• temperatura Ts della superficie di scambio, ovvero delle pareti dei tubi.

• temperatura media di massa del fluido Tm, valutabile come la media tra la

temperatura di ingresso e quella di uscita del liquido. • temperatura media del film Tf, definita come 0.5(Tm+Ts).

Si definisce inoltre la quantità Gmax, data dal flusso di massa del liquido m&_L

diviso per la minima sezione di passaggio Amin, che ovviamente dipenderà dalla

disposizione dei tubi. Le configurazioni più comuni sono riportate nella seguente figura

Figura 6.10 Possibili disposizioni dei tubi nel banco.

dove SL e ST sono rispettivamente il passo longitudinale e quello trasversale tra le

file, che generalmente assumono valori compresi tra 1.25 e 1.5 volte il diametro esterno dei tubi. La sezione minima di passaggio, sarà allora data da:

(

S_T−d_e

)

L nel caso a) di tubi allineati L d S S2L 2T e⎟_⎠⎞ ⎜ ⎝

⎛ _{+ − nel caso b) di tubi sfalsati.}

Sperimentalmente è stato dimostrato che il parametro adimensionale che governa il flusso attraverso il banco di tubi è il cosiddetto numero di Reynolds di massa, definito come

m e max max d G Re µ = (6.58)

dove µm è la viscosità del fluido riferita alla temperatura Tm. Il regime di moto del

fluido è laminare per Remax<200, turbolento per Remax>6000 e di transizione negli

altri casi.

Per il problema in esame i valori di Remax in gioco sono, come emerge da studi

preliminari, dell’ordine di poche centinaia e quindi a cavallo tra il regime di flusso laminare e quello di transizione. In questo caso possono essere utilizzate le seguenti correlazioni empiriche per il coefficiente medio di scambio termico hL,

(

)

⎪ ⎨ ⎧ ≥ × = ⎟ ⎟ ⎞ ⎜ ⎜ ⎛_µ 1 perN 10 j Pr h f 14 . 0 s 3 / 2 m L _(6.59)

dove i pedici indicano a quale temperatura sono riferite le rispettive quantità, e per la perdita di carico per attrito

25 . 0 m s f 2 max f N G 2 p _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ µ µ ρ ′ = ∆ f (6.60)

Nelle (6.59) e (6.60) Nf indica il numero di file di tubi nella direzione del moto del

fluido. I valori dei coefficienti j e f′ sono stati determinati sperimentalmente, al variare del numero di Reynolds di massa e della disposizione dei tubi, come riportato in Figura 6.11.

Figura 6.11 Fattore di attrito f’ e fattore di Colburn j per il moto trasversale di un fluido su un banco di tubi al variare del numero di Reynolds, per varie disposizioni dei tubi ([5],[6]).

Sia la (6.59) che la (6.60) richiedono la conoscenza della temperatura alla parete, che non è nota, ma è calcolabile attraverso la relazione:

(

s m

)

g

(

g s

)

L T T h T T

h

Q& = − = ε − _(6.61) dove Tg è la temperatura media del gas e dove al solito si è trascurato l’effetto

della conduzione attraverso la parete. Poiché generalmente sarà h_L >>h_gε è ragionevole ritenere che la temperatura alla parete sia molto prossima a quella

del liquido. La soluzione del sistema (6.59) - (6.61) può allora essere ottenuta itera-tivamente partendo dalla condizione µs/µm=1.

Oltre alle perdite per attrito date dalla (6.61) si dovrà considerare anche le perdite concentrate di immissione ed emissione del fluido dallo scambiatore

out 2 out in 2 in f tot V k 2 1 k V 2 1 p p =∆ + ρ + ρ ∆ (6.62)

dove Vin e Vout sono le velocità del flusso rispettivamente all’interno del condotto in

ingresso e di quello d’uscita e coincidono se i diametri dei due condotti sono uguali. Per la determinazione dei fattori di perdita kin e kout si è fatto riferimento

rispettivamente al caso di brusco allargamento, per il quale i manuali riportano kin=1.0, e imbocco non raccordato kout=0.5.

Dalla (6.62) e (6.60) è possibile ricavare l’espressione della resistenza idraulica dello scambiatore ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + π ρ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ µ µ ρ ′ = 4 out out 4 in in 2 25 . 0 m s min f exg D k D k 8 A N 2 R 2 f _(6.63)

6.5.2 Coefficiente di attrito e di scambio termico per il gas

Per quanto riguarda il flusso del gas nei tubi, il numero di Reynolds riferito al diametro può essere scritto

ε π µ = e g D d N m 4 Re & (6.64)

Convenzionalmente si considera il flusso laminare per ReD al di sotto di 2100

dopodiché si entra nella fase di transizione fino a raggiungere un moto completamente turbolento per ReD superiori a 10000. Nel passaggio da regime

laminare a regime di transizione si ha un repentino aumento del coefficiente di scambio termico e perciò sarà conveniente, attraverso un’opportuna scelta del prodotto Nde, far sì che ReD risulti il più vicino possibile alla zona turbolenta. Ad

esempio, poiché si ha m& =2.57x10_g -2 _{kg/s e considerando una temperatura media}

del gas di 700 K (per la quale dalla formula di Sutherland si ha µ=3.31x10-5

kg/ms), per ottenere ReD=5000 si dovrà avere Nd_eε≅198mm, ovvero se de=9mm

ed essendo ε≅1 saranno necessari 22 tubi.

Purtroppo l’attuale comprensione dei fenomeni di scambio termico in regime di transizione non è ancora completa e non esistono modelli di validità generale, in quanto la situazione può variare significativamente da caso a caso. In questa

analisi, che vuol essere puramente preliminare, si supporranno valide le correlazioni determinate per il flusso completamente turbolento, ovvero

3 / 2 f 2 . 0 i f pg g _Pr Gd 023 . 0 G c h ₋ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ µ = (6.65)

dove il pedice f indica, ancora una volta, che si considera la temperatura media del film. Per quanto riguarda il fattore di attrito può essere utilizzata ancora la relazione di Karman-Nikuradse6 _{(6.15), considerando un fattore correttivo che}

tenga conto degli effetti dello scambio termico

14 . 0 m s isot ff T T ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = f fe (6.66)

dove fisot è il valore isotermo calcolato con la (6.15) e feff è il valore effettivo.

6.5.3 Perdita di pressione nel gas Con riferimento alla Figura 6.12,

Figura 6.12 Schema del passaggio del gas attraverso lo scambiatore.

la perdita di pressione7 _{subita dal gas nell’attraversare lo scambiatore è dovuta a:}

6 _{la formula di Karman-Nikuradse è valida per tubi lisci, comunque dal}

diagramma di Moody (figura 6.3), è possibile vedere come a numeri di Reynolds dell’ordine di 4000-5000 gli effetti della rugosità siano abbastanza modesti, almeno per tubi di buona qualità.

• brusco allargamento della sezione di ingresso. Supponendo che l’allargamento sia leggermente raccordato è possibile considerare un fattore di perdita k=0.9,

( )

V 0.9 2 1 p p i 2 0 i ₌ ρ − (6.67)

• perdite per imbocco nel banco di tubi. In questo caso i manuali riportano per k il valore 0.5

( )

V 0.5 2 1 p p 1 2 1 0 ₌ ρ − (6.68)

Le condizioni del flusso al punto 1 sono state calcolate considerando la densità costante tra i ed 1.

• perdite per attrito lungo il tubo. In realtà lungo il tubo si ha anche un lieve recupero di pressione dovuto alla sottrazione di calore che però a bassi numeri di Mach risulta praticamente ininfluente. Sfruttando i risultati del paragrafo precedente si ha perciò:

( )

i eff 1 2 2 1 d L V 2 1 p p f = ρ − (6.69)

• perdite per sbocco dal banco di tubi. Considerando lo sbocco dai tubi come un brusco allargamento della sezione si dovrà considerare k=1.0, e quindi

( )

V 1.0 2 1 p p 2 2 3 2 ₌ ρ − (6.70)

A parte la pressione, tutte le altre variabili sono dominate dallo scambio termico, perciò le proprietà del flusso al punto 2 possono essere calcolate mediante le note relazione del flusso monodimensionale in un condotto a sezione costante e variazione di temperatura totale.

(

)

(

)

2 1 2 2 2 2 2 2 2 1 2 1 2 2 1 2 01 02 M M M 1 M 1 M M T T T T ≅ γ + γ + = ≅ (6.71) 2 1 2 2 2 2 2 1 2 1 2 2 1 2 2 1 M M M 1 M 1 M M V V _≅ γ + γ + = = ρ ρ _(6.72)

Conoscendo la variazione di temperatura, è possibile ricavare M2 dalla prima e

sostituirlo nella seconda in modo da ottenere densità e velocità del flusso in uscita dal banco di tubi.

• perdite per imbocco nel condotto di uscita. Anche qui, considerando un leggero raccordo si può supporre k=0.3 e di conseguenza

( )

V 0.3 2 1 p p e 2 e 3 ₌ ρ − _(6.73)

dove i valori di ρe e Ve sono determinati imponendo la conservazione della massa e

supponendo che la densità si mantenga costante tra 2 ed e.

Ricapitolando, la perdita totale di pressione può essere espressa da

( )

(

)

_⎪⎭⎪⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ β + + + α + = ρ − 2 1 2 i eff 2 i 2 e i _{1 0.3} T T d L 5 . 0 1 9 . 0 V 2 1 p p f (6.74)

dove α è il rapporto tra la sezione di passaggio all’interno del banco dei tubi e quella del condotto in ingresso, mentre β è l’analogo per la sezione del condotto in uscita.

6.6

Risultati principali

In questo paragrafo si riportano i risultati più significativi ottenuti con la procedura di calcolo descritta nei paragrafi precedenti

6.6.1 Risultati relativi al diffusore

Per quanto riguarda il diffusore il problema è stato affrontato nel seguente modo. Si sono scelti come parametri indipendenti la posizione dell’onda d’urto, rappresentata dal rapporto tra il numero di Mach dell’urto stesso e quello all’ingresso del divergente

1 , div sh M M f =

e il rapporto dei diametri del convergente dato da Dgola/Din.

• angoli θ di semiapertura del tratto convergente e del tratto divergente rispettivamente pari a 6.5° e 2.5°.

• diametro esterno ed interno del tubo dell’avvolgimento elicoidale di raffreddamento pari rispettivamente a 10 mm e 9 mm.

• lunghezza della gola del diffusore uguale a 60 mm.

• incremento della temperatura dell’acqua di raffreddamento pari a 50°C.

Le variabili dipendenti sono, invece: le condizioni di ristagno del gas all’uscita del diffusore, il flusso di massa di refrigerante necessario e la sua perdita di pressione, la lunghezza complessiva del diffusore e il suo diametro di uscita.

I risultati ottenuti sono stati riportati graficamente nelle seguenti Figura 6.13-Figura 6.18 e numericamente nella Tabella 6.1.

Figura 6.13 Temperatura di ristagno

Figura 6.15 Lunghezza complessiva

del diffusore. diffusore. Figura 6.16 Diametro all’uscita del

Figura 6.17 Portata di acqua

Dth/Din f p0 [Pa] p [Pa] T0 [K] ρ [kg/m3_] Dex [mm] Ldiff [mm] ∆ploss [bar] w [g/s] 1.0 53317 53004 1402 0.131 60.2 658 0.25 36.2 1.1 43015 42744 1396 0.106 64.9 712 0.28 36.8 1.2 33947 33729 1389 0.084 72.0 793 0.34 37.6 1.3 26384 26211 1383 0.066 82.2 910 0.44 38.6 0.34 1.4 20293 20163 1376 0.051 94.7 1054 0.58 39.6 1.0 49070 48772 1410 0.120 62.6 660 0.25 35.3 1.1 38400 38162 1402 0.095 69.6 741 0.30 36.1 1.2 29421 29235 1394 0.073 78.3 840 0.38 37.0 1.3 22246 22103 1387 0.055 90.0 975 0.50 38.0 0.36 1.4 16680 16572 1380 0.042 103.4 1128 0.65 38.8 1.0 44951 44684 1416 0.110 65.7 671 0.25 34.6 1.1 34099 33871 1410 0.084 72.8 752 0.31 35.4 1.2 25367 25202 1401 0.063 85.4 896 0.42 36.5 1.3 18672 18550 1393 0.046 98.7 1049 0.56 37.5 0.38 1.4 13659 13570 1385 0.034 115.2 1238 0.76 38.4

Tabella 6.2 Risultati numerici relativi al calcolo del convergente.

Come si vede, avere un basso valore del parametro f migliora le prestazioni sotto praticamente tutti i punti di vista. Questo fatto d’altronde, era largamente prevedibile alla luce delle considerazioni fatte nel capitolo 4. Come sarà messo in luce in seguito, la posizione dell’urto normale è determinata dalla pressione a valle, che a sua volta dipende dal sistema di pompaggio. In seguito ad una perturbazione che faccia salire la pressione a valle, può accadere che l’urto entri all’interno della gola e sia spinto fuori dal tratto convergente. E’ perciò opportuno selezionare un valore di f sufficientemente maggiore di 1, in modo da fornire una certa robustezza a questo genere di disturbi. Se si suppone che la massima ampiezza dei disturbi sulla pressione sia pari al 10% del valore nominale, dai valori della Tabella 6.2 si ottiene che un valore di sicurezza può essere f=1.06.

Per quanto riguarda la perdita di pressione del refrigerante nell’avvolgimento elicoidale, si è trovato che essa corrisponde a circa la metà della caduta di pressione complessiva nel circuito. Un possibile modo di ridurre tali perdite è illustrato in Figura 6.19, sostituendo all’avvolgimento unico due avvolgimenti connessi tra loro in parallelo.

Figura 6.19 Due possibili suddivisioni dell’avvolgimento elicoidale in due avvolgimenti connessi in parallelo.

Il modello di calcolo descritto in precedenza per l’avvolgimento unico può essere facilmente adattato per trattare il caso b) semplicemente suddividendo il problema in due parti. Ad esempio, si può considerare che un avvolgimento interessi convergente e divergente e l’altro il tratto divergente, oppure la divisione può essere fatta in modo che la potenza termica scambiata dai due avvolgimenti sia all’incirca la stessa. Per il caso a) la questione è un po’ più complicata poiché la geometria del condotto indebolisce le ipotesi su cui si basa il modello. Tuttavia, un modo per adattare, anche a questa situazione, il metodo basato sulla suddivisione dell’avvolgimento in spire può essere quello di considerare le spire pari appartenenti ad un elica, mentre quelle dispari appartenenti all’altra.

Gli effetti della suddivisione in due dell’avvolgimento possono essere, approssimativamente, valutati in modo molto semplice. Nelle ipotesi che:

• i due avvolgimenti abbiano una resistenza pari alla metà di quella dell’avvolgi-mento singolo.

• la portata volumetrica Qcoil complessivamente destinata al raffreddamento del diffusore resti invariata (questa ipotesi comporta che l’incremento di tempera-tura subito dal fluido rimanga, in prima approssimazione, lo stesso che nel caso di avvolgimento singolo).

si ottiene una resistenza equivalente, e quindi una perdita di pressione, pari a 1/8 di quella relativa al singolo avvolgimento. I benefici di questa nuova disposizione sono visualizzati in Figura 6.20.

Figura 6.20 Perdita di pressione subita dal refrigerante nel caso di due avvolgimenti elicoidali connessi in parallelo.

6.6.2 Risultati dell’impianto completo

Per i calcoli relativi allo scambiatore si è adottato, come parametro indipendente, la temperatura del gas in uscita e sono stati imposti i seguenti vincoli:

• tubi disposti in modo allineato (caso a di Figura 6.10) con 6 tubi per ogni fila trasversale al flusso.

• sezione di passaggio complessiva del gas nel banco di tubi pari ad α=1.1 volte quella di ingresso. Questa condizione è necessaria per evitare la presenza di una terza sezione ristretta nel condotto.

• diametro esterno dei tubi di 10 mm e spessore di 0.5 mm. • passo tra le file di tubi pari a 1.25 volte il diametro esterno. • temperatura dell’acqua in uscita non superiore a 50°C.

I parametri relativi allo scambiatore, che si vuole determinare sono: il flusso di massa di liquido necessario allo scambiatore, la superficie di scambio termico complessiva e la perdita di pressione nel liquido. Per quanto riguarda il diffusore, le ipotesi del paragrafo precedente rimangono inalterate e inoltre si fissa per Dth/Din il valore 0.34.

La portata volumetrica della pompa che consente il funzionamento continuo della galleria sarà data da:

p RT m m V& & = &

ρ

= (6.75)

dove p e T sono rispettivamente la pressione e la temperatura del gas in ingresso alla pompa. Assumendo T come variabile indipendente la pressione p risulterà funzione di T ed f come rappresentato in Figura 6.21.

Figura 6.21 Pressione del gas in ingresso alla pompa in funzione della posizione dell’onda d’urto e della temperatura del gas in uscita dallo scambiatore.

I corrispondenti valori della portata volumetrica della pompa V&, calcolati mediante la (6.75), sono dati in Figura 6.22.

Figura 6.22 Portata volumetrica della pompa richiesta per il funzionamento continuo, in funzione della posizione dell’onda d’urto e della temperatura del gas in uscita dallo scambiatore.

Figura 6.23 Superficie totale di scambio termico dello scambiatore in funzione della posizione dell’onda d’urto e della temperatura del gas in uscita dallo scambiatore.

La Figura 6.23 mostra la superficie di scambio termico tra gas e liquido necessaria allo scambiatore, per portare il gas alla temperatura di uscita desiderata. Ovviamente minore è la temperatura che si vuole ottenere maggiore è la superficie richiesta. Si noti che, per una stessa configurazione, il costo dello scambiatore può ritenersi approssimativamente proporzionale alla superficie di scambio e quindi è conveniente che il suo valore sia il più basso possibile.

La Figura 6.24 mostra la lunghezza richiesta per i tubi dello scambiatore, mentre il numero totale di tubi è riportato in Tabella 6.3. Si noti che, in virtù dell’ipotesi sulla sezione di passaggio nel banco, tale numero risulta indipendente dalla temperatura di uscita del gas.

Figura 6.24 Lunghezza dei tubi dello scambiatore in funzione della posizione dell’onda d’urto e della temperatura del gas in uscita dallo scambiatore.

f Numero di _tubi 1.0 50 1.1 58 1.2 71 1.3 92 1.4 122

Tabella 6.3 Numero complessivo di tubi nel banco al variare della posizione dell’urto.

Figura 6.25 Portata di fluido richiesta dallo scambiatore in funzione della posizione dell’onda d’urto e della temperatura del gas in uscita dallo scambiatore.

Figura 6.26 Prevalenza della pompa richiesta in funzione della posizione dell’onda d’urto e della temperatura del gas in uscita dallo scambiatore.

La Figura 6.25 mostra la portata di massa di acqua richiesta dallo scambiatore che logicamente dipende fortemente dalla temperatura di uscita dei gas. La portata che attraversa lo scambiatore coincide con quella complessivamente circolante nel circuito, ovvero è la somma di quella che fluisce nell’avvolgimento attorno al diffusore più quella di bypass. Confrontando la Figura 6.25 con la Figura 6.17 si vede che il rapporto m&coil m&tot assume valori compresi tra 0.1 e

0.15.

Nella Figura 6.26 è invece mostrata la prevalenza richiesta alla pompa del refrigerante per vincere le perdite nel circuito, nel caso di doppio avvolgimento elicoidale. La dipendenza dalla temperatura di uscita del gas è trascurabile, mentre la dipendenza dalla posizione dell’onda d’urto è legata prevalentemente alla lunghezza del diffusore.

Bibliografia del Capitolo 6

[1]. Citrini D., Noseda G. – “Lezioni di Idraulica”, Tamburini Ed., 1971.

[2]. Davis C.V., Sorensen K.E. – “Handbook of Applied Hydraulics” – , McGraw-Hill Book Co., 1969.

[3]. Rouse H., “ Engineering Hydraulics”, John Wiley & Sons, 1950.

[4]. Moody, L.F., “Friction Factors for Pipe Flow”, Trans. A.S.M.E., Vol. 66, 1948. [5]. Kreith, F., – “Principals of Heat Transfer” – HarperCollins Publishers, 1948 [6]. Shao Ti Hsu, – “Engineering Heat Transfer” – D. Van Nostrand Company Inc.,

1963.

[7]. Mori Y., Nakayama W., “Study on forced convective heat transfer in curved pipes (1st Report, laminar region)”, International Journal of Heat and Mass Transfer, Vol.8, 1965.

[8]. Mori Y., Nakayama W., “Study on forced convective heat transfer in curved pipes (2st Report, turbulent region)”, International Journal of Heat and Mass Transfer, Vol.10, 1967.

[9]. Dean, W.R. ”Note on the motion of fluid in a curved pipe”, Philosophical Magazine, Series 7, Vol. 4, 1927.

[10]. Dean, W. R. “The streamline motion of fluid in a curved pipe. Philosophical Magazine, Series 7, Vol. 5, 1928.

[11]. White, C.M. “Streamline flow through curved pipes” Proceedings of the Royal Society of London, Series A, Vol. 123, 1929.

[12]. Dravid, A.N., Smith, K.A., Merrill K.A., and Brian K.A., “Effect of secondary fluid motion on laminar flow heat transfer in helically coiled tubes”, AIChE Journal, Vol. 17, 1971.

[13]. Ito, H. “Friction factors for turbulent flow in curved pipes”, Journal of Basic Engineering, Transactions of the ASME, Vol. 81, 1959.

[14]. Van Driest, E.R. “Turbulent Boundary Layer in Compressible Flows”, Journal of the Aeronautical Sciences, Vol. 18, No. 3, 1951.