1. 2. 3. 4.

1.

2.

3.

4.

5. ANALISI DEL COMPORTAMENTO DINAMICO DEL

VELIVOLO RIGIDO.

5.1 - INTRODUZIONE.

Analizzate le condizioni di trim compatibili con le caratteristiche aerodinamiche della macchina si è interessati a conoscere il comportamento del velivolo in seguito a manovre prescritte nella normativa FAR 25.255(a), al fine di determinare i massimi carichi agenti sulla coda orizzontale. La dinamica connessa alle manovre studiate riguarda il piano longitudinale: si tratta sempre di condizioni di volo in cui la traiettoria seguita è contenuta nel piano di simmetria per il velivolo stesso, costituito dal piano verticale virtuale passante per l’asse longitudinale della fusoliera. L’analisi che segue viene effettuata facendo uso di equazioni di moto scritte in una terna assi stabilità, definita nel precedente paragrafo 2.5, ipotizzando che la struttura del velivolo sia infinitamente rigida. Tale dinamica si sviluppa con l’azionamento del comando d’equilibratore, la cui superficie viene fatta ruotare secondo opportune leggi temporali.

5.2 - MODELLO ANALITICO PER LO STUDIO DELLA DINAMICA.

Lo studio del comportamento dinamico del velivolo è svolto mediante le equazioni longitudinali del moto (tabelle 5.1, 5.2) valutate in assi stabilità ed in assenza di disturbi atmosferici, quali vento o forti raffiche, discusse in precedenza nei paragrafi 2.3 - 2.5. Definita una generica condizione di trim, ovvero una condizione di volo rettilineo orizzontale con ali livellate, angolo d’imbardata nullo e vettore velocità appartenente al piano longitudinale di simmetria, si valutano le variazioni delle componenti di tale vettore, ossia la variazione di velocità orizzontale u e verticale oltre alla variazione di velocità angolare , conseguenti l’azionamento da parte del pilota del comando d’equilibratore. Operando in questo modo si determinano le risposte del velivolo e quindi si possono calcolare le variazioni delle sollecitazioni alle quali è sottoposta la coda orizzontale.

w

Nel fare questo studio si segue inizialmente un primo livello di approssimazione, adottando il modello della dinamica di corto periodo (tabella 5.1). Tale modello ha tempi caratteristici di evoluzione dell’ordine di qualche secondo ed è generalmente caratterizzato da trascurabili variazioni della componente longitudinale della velocità u. Si ottiene a partire dal modello completo a tre gradi di libertà della dinamica del velivolo trascurando l’equazione relativa al moto nella direzione dell’asse X e tutti i termini in u che compaiono nelle due rimanenti equazioni, relative rispettivamente al moto nella direzione dell’asse ed intorno all’asse Y .

S

S

Z _S

Successivamente viene analizzato il più dettagliato modello completo a tre gradi di libertà di seguito riportato (tabella 5.2). Ciò richiede la ricostruzione di alcune derivate aerodinamiche del velivolo in assi stabilità quali: X , , , , non note sperimentalmente ma legate a caratteristiche aerodinamiche della macchina in precedenza valutate. A tale proposito si fa notare che i termini che compaiono nella prima equazione del modello completo legati alle derivate aerodinamiche X ed , possono essere trascurati senza commettere un errore significativo. Infatti, una perturbazione di velocità angolare di beccheggio q comporta principalmente una variazione della portanza sulla

coda del velivolo con conseguente variazione di portanza globale, ovvero risulta diverso da zero il termine , ma implica una trascurabile variazione di resistenza aerodinamica tale da ritenere nullo il contributo .

u Xw q u Z w X_& u M q Z_q q X_q

Analogamente si può ritenere trascurabile il termine , in quanto anche l’effetto del ritardo di “downwash” si traduce principalmente in una variazione di portanza in coda senza effetti significativi sulla resistenza. Si rileva esplicitamente che questi risultati sono validi solo in assi stabilità e non in assi corpo generici. Inoltre è bene precisare che in assi stabilità le derivate in u sono nulle perché una variazione di u non induce una corrispondente variazione dell’angolo d’incidenza. Ne conseguono: .

w X_{w& &} & 0 = = _u u M Z

X_u& = _{& &}

Le derivate aerodinamiche in w, quali Z ed , rappresentano fisicamente il ritardo aerodinamico che ha effetto principalmente sulla portanza in coda: una variazione di incidenza in ala si traduce in una corrispondente variazione dell’angolo di “downwash” in coda. Tale variazione non avviene istantaneamente, ma con un ritardo ∆ proporzionale alla distanza ala-coda divisa per la velocità di volo del velivolo. Dunque, si assume che il “downwash” sulla coda all’istante attuale sia funzione del valore della portanza e quindi

& w&

t

w

M_&

e X w Z q Z w Z Vq

w& = + _w + _q + _w& &+ _δeδ

e M w M q M w M

q_&= _w + _q + _{w& &}+ _δeδ

q

=

θ&

Tab. 5.1: Equazioni longitudinali del moto in assi stabilità, in assenza di vento o raffica, secondo il modello della dinamica di corto periodo.

w X u X g w X q X w X u X g

u_&=− θ + _u + _w + _q + _{w& &} ≅− θ + _u + _w

e X w Z q Z w Z u Z Vq

w_& = + _u + _w + _q + _{w& &} + _δeδ

e M w M q M w M u M

q_&= _u + _w + _q + _{w& &} + _δeδ

q

=

θ&

VARIABILI AGGIUNTIVE IN TERMINI DI VARIAZIONI

V w wb = ∆α wb α θ γ =∆ −∆ g w Vq n_Z = − & ∆

Tab. 5.2: Equazioni longitudinali del moto in assi stabilità, in assenza di vento o raffica, secondo il modello della dinamica a tre gradi di libertà.

dell’incidenza dell’ala al tempo t−∆t.

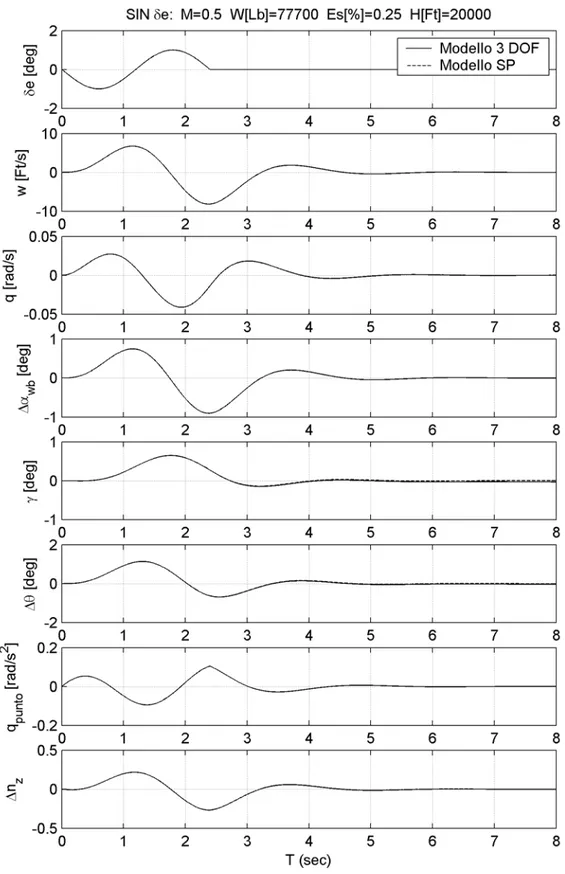
A titolo d’esempio nelle figure 5.1 – 5.2 che seguono sono riportate sovrapposte alcune risposte del velivolo secondo i due modelli ad opportuni comandi d’equilibratore, come di seguito indicato, con ampiezza massima unitaria per una condizione di volo a mach 0.50 e quota di 20000 Ft. I comandi applicati hanno rispettivamente un andamento “a rampa” e sinusoidale tali da far cabrare il velivolo. Le risposte vengono valutate per un tempo pari a 5 secondi a partire dall’azionamento del comando, ovvero dall’istante in cui la superficie di controllo dell’equilibratore inizia a ruotare verso l’alto. Si riscontra un ottimo grado d’approssimazione del modello di corto periodo: i risultati forniti cominciano a differenziarsi da quelli ottenuti dal modello completo solo quando ormai è avvenuta l’estinzione del modo di corto periodo. Alla luce di questi risultati è giustificata l’adozione del modello di corto periodo nel seguito di questo lavoro.

Mediante l’analisi delle risposte temporali si vuole conoscere l’evoluzione della dinamica nel corto periodo al fine di valutare la massima escursione delle sollecitazioni agenti sulla coda del velivolo che si manifestano entro pochi secondi dalla rotazione della superficie dell’equilibratore da parte del pilota.

Le condizioni di regime di corto periodo per il velivolo in esame sono raggiunte generalmente entro 5-10 secondi dall’azionamento del comando. Dal modello di corto si determinano gli autovalori della matrice degli stati che costituiscono i poli del sistema risultante. Tali autovalori coincidono con le radici, generalmente complesse, del seguente polinomio caratteristico:

( )

[

]

(

2 ₂ 2

)

SP SP SP SP LONG S = S + ω ς +ω ∆

I fattori ω_SP e ς_SP rappresentano rispettivamente la pulsazione e lo smorzamento della coppia di poli complessi coniugati: i valori di pulsazione e smorzamento sono noti in funzione delle stesse derivate aerodinamiche del velivolo. Per questi valgono le relazioni che seguono [7], [15]:

Fig. 5.1: Confronto delle risposte del velivolo al comando a rampa d’equilibratore nelle condizioni di volo indicate, fornite dal modello completo e di corto periodo.

Fig. 5.2: : Confronto delle risposte del velivolo al comando sinusoidale d’equilibratore nelle condizioni di volo indicate, fornite dal modello completo e di corto periodo.

(

)

1/2 α ω_SP = Z_wM_q −M

(

)

SP q w SP M M Z ω ξ α 2 & + + − =

Il modo di corto periodo è caratterizzato da elevata pulsazione e forte smorzamento. Ovviamente l’effettivo valore dei poli dipende dai parametri che caratterizzano l’intero sistema, quali la velocità di volo, i valori delle derivate aerodinamiche, dipendenti quest’ultimi dalla quota, dal numero di mach e dall’architettura del velivolo. Poiché per un sistema del secondo ordine puro il tempo d’assestamento è dell’ordine di

SP SP a _{ω ς} 4 = t , si

può ricavare in modo esplicito la durata del corto periodo per ogni condizione di volo esaminata.

In conclusione sono note tutte le caratteristiche del moto del velivolo secondo una dinamica di corto periodo negli istanti immediatamente successivi la rotazione dell’equilibratore nei quali, come detto, il piano di coda orizzontale è maggiormente sollecitato.

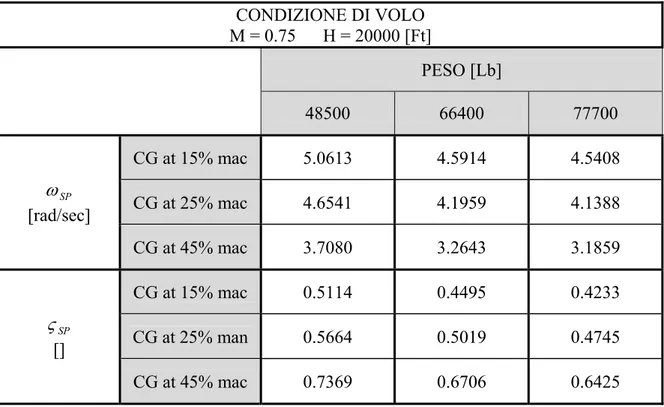
A titolo di esempio nelle tabelle 5.3, 5.4, 5.5 che seguono sono riportati i più significativi valori di ω_SP e ς_SP relativi a condizioni di volo per mach 0.20 a bassa quota e mach 0.75 ad alta quota.

CONDIZIONE DI VOLO M = 0.20 H = SL PESO [Lb] 48500 66400 77700 CG at 15% mac 1.9906 1.8173 1.8071 CG at 25% mac 1.8735 1.7041 1.6930 SP ω [rad/sec] CG at 45% mac 1.6132 1.4515 1.4378 CG at 15% mac 0.6415 0.6114 0.6013 CG at 25% man 0.6923 0.6621 0.6520 SP ς [] CG at 45% mac 0.8287 0.8011 0.7617

Tab. 5.3: Pulsazione e smorzamento di corto periodo nelle condizioni indicate.

CONDIZIONE DI VOLO M = 0.75 H = 20000 [Ft] PESO [Lb] 48500 66400 77700 CG at 15% mac 5.0613 4.5914 4.5408 CG at 25% mac 4.6541 4.1959 4.1388 SP ω [rad/sec] CG at 45% mac 3.7080 3.2643 3.1859 CG at 15% mac 0.5114 0.4495 0.4233 CG at 25% man 0.5664 0.5019 0.4745 SP ς [] CG at 45% mac 0.7369 0.6706 0.6425

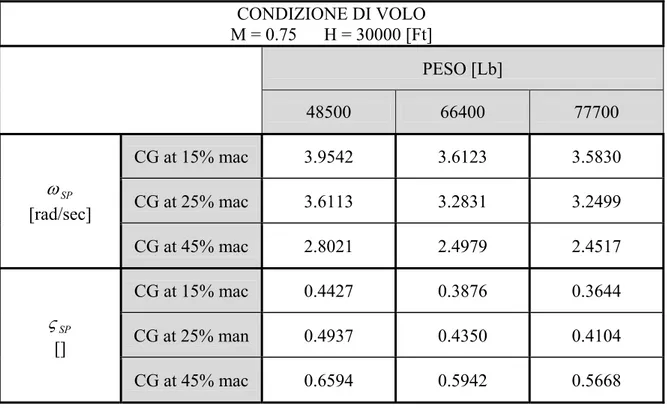
CONDIZIONE DI VOLO M = 0.75 H = 30000 [Ft] PESO [Lb] 48500 66400 77700 CG at 15% mac 3.9542 3.6123 3.5830 CG at 25% mac 3.6113 3.2831 3.2499 SP ω [rad/sec] CG at 45% mac 2.8021 2.4979 2.4517 CG at 15% mac 0.4427 0.3876 0.3644 CG at 25% man 0.4937 0.4350 0.4104 SP ς [] CG at 45% mac 0.6594 0.5942 0.5668

Tab. 5.5: Pulsazione e smorzamento di corto periodo nelle condizioni indicate.

5.3 - COMANDI DI INGRESSO PER LA SIMULAZIONE NUMERICA.

Per effettuare un’analisi dei carichi strutturali ai quali è sottoposta la coda orizzontale di un velivolo da trasporto commerciale in condizioni di volo simmetrico, vengono considerate le seguenti manovre (da effettuarsi in precise condizioni operative identificate sui diagrammi di manovra):

• Brusca manovra di richiamata per una incontrollata rotazione verso l’alto e verso il basso dell’equilibratore a fattori di carico di progetto.

• Manovra connessa ad una rotazione controllata dell’equilibratore a fattori di carico di progetto.

In entrambi i casi, tali manovre richiedono una singola e rapida rotazione della superficie del comando d’equilibratore da effettuarsi rispettando un’opportuna legge di moto prestabilita. Secondo la normativa FAR/JAR 25.337 (b) e (c) e FAR/JAR 25.345 (a) (1) e

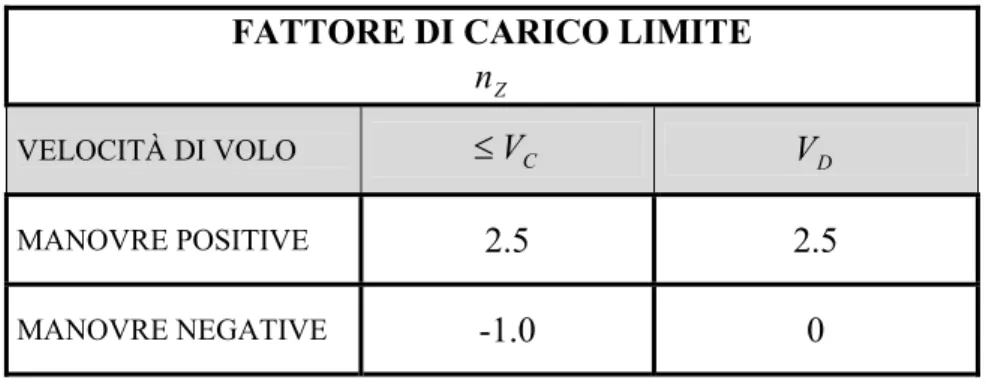
(d), il valore limite del fattore di carico a cui il velivolo può essere sottoposto in seguito a manovre simmetriche nella condizioni di “flaps up”, è 2.5 per manovre a fattore di carico positivo (“manovre positive”), mentre per manovre a fattore di carico negativo o nullo (“manovre negative“) vale: -1.0 per velocità di volo inferiori alla velocità di progetto per la crociera ; 0 per una velocità pari alla massima velocità in affondata, generalmente indicata con V . Tali condizioni sono riassunte nella tabella 5.10.

C

V

D

FATTORE DI CARICO LIMITE

Z

n

VELOCITÀ DI VOLO ≤V_C V_D

MANOVRE POSITIVE 2.5 2.5

MANOVRE NEGATIVE -1.0 0

Tab. 5.6: Fattori di carico massimi consentiti dalla normativa per manovre simmetriche.

I regolamenti FAR 25.331 (c) richiedono che l’analisi connessa ad una brusca manovra di richiamata non controllata venga effettuata alla velocità di progetto per la manovra in corrispondenza della quale si assume che la macchina stia procedendo in volo orizzontale livellato, in condizioni di equilibrio stabile a fattore di carico unitario: si richiede che, compatibilmente con il massimo sforzo esercitabile dal pilota sulla barra di comando, la superficie dell’equilibratore venga fatta ruotare molto rapidamente, per ottenere la massima accelerazione in beccheggio fino al raggiungimento del valore limite consentito del fattore di carico identificato per ciascuna condizione sul relativo diagramma di manovra. Per determinare il carico in coda occorre valutare la risposta dinamica del velivolo ed analizzare il transitorio di tale risposta prima del raggiungimento della condizione di regime nella dinamica di corto periodo. I carichi strutturali che si hanno in seguito ad una accelerazione normale del baricentro del velivolo, qualora venga oltrepassato il valore limite positivo massimo del fattore di carico n imposto per la manovra, non devono essere presi in considerazione. La brusca manovra di richiamata per una incontrollata rotazione verso l’alto dell’equilibratore, può essere analiticamente

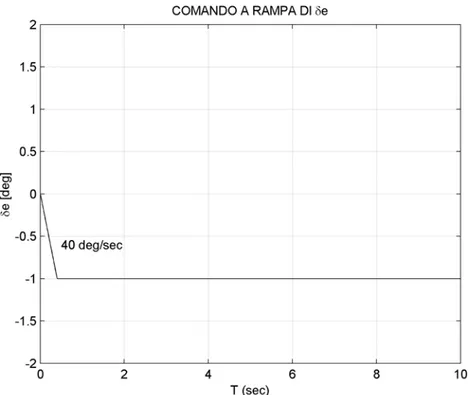
ricostruita considerando, come comando di ingresso per descrivere il moto della superficie di comando, una rampa lineare con velocità iniziale costante, pari a 40 deg/sec, che impiega un tempo di 0.40 secondi per raggiungere la massima rotazione possibile per la superficie mobile. Oltre tale istante l’equilibratore viene mantenuto nella posizione di massima deflessione raggiungibile in ogni condizione.

Per la normativa FAR 25.331 (c) (1) la rotazione massima disponibile e richiesta per la simulazione di una manovra non controllata è limitata o dal raggiungimento del valore limite consentito del fattore di carico, o dai fermi di fine corsa della superficie mobile dell’equilibratore, o dal massimo sforzo di barra esercitabile dal pilota stimato in 300 Lb, oppure dalla capacità di potenza dell’unità di controllo del movimento della superficie mobile medesima. In base ai dati a disposizione relativi al velivolo di riferimento, si assume una rotazione massima disponibile, consentita dall’architettura del piano di coda orizzontale, pari a ±15 deg.

Per una manovra controllata basata su una rotazione razionale dell’equilibratore, deve essere stabilito in quali condizioni il valore limite di progetto del fattore di carico, specificato nella FAR 25.337 precedentemente menzionata, non viene superato. La risposta del velivolo deve essere caratterizzata da un’accelerazione in beccheggio non inferiore a prefissati valori, dipendenti anche dalle caratteristiche della macchina. Per effettuare l’analisi dei carichi connessi alla manovra controllata, come indicato nel riferimento [3], si assume che l’aereo si trovi in una condizione d’equilibrio stabile ad una velocità compresa tra la velocità di progetto per la crociera e la massima velocità in affondata, quando l’equilibratore viene rapidamente deflesso secondo una legge di moto di tipo sinusoidale: la superficie mobile ruota rapidamente in una direzione per poi tornare indietro oltrepassando la posizione di trim originaria fino al massimo consentito riportandosi infine nella posizione di partenza. La legge di moto seguita dalla superficie mobile in termini di angolo di deflessione δ , è definita analiticamente dalla seguente espressione: e

(

t

)

e

e δ ω_SP

δ = ₀sin

L’ampiezza δe₀ della funzione è data dall’angolo d’equilibratore richiesto per raggiungere un valore limite di progetto predefinito del fattore di carico od eventualmente dal massimo angolo di deflessione disponibile, nel caso in cui la massima rotazione non

comporta il raggiungimento del valore limite massimo consentito di n . La pulsazione della funzione sinusoidale rappresenta la velocità angolare della superficie mobile, ed è selezionata pari alla pulsazione naturale del modo rigido di corto periodo in beccheggio

Z

SP ω .

A titolo di esempio nelle figure 5.3 e 5.4 che seguono sono rappresentate graficamente le due distinte leggi di moto della superficie mobile, di ampiezza massima unitaria (1 [deg] ), impiegate nella simulazione delle manovre.

Fig. 5.3: Legge di moto dell’equilibratore per un comando a rampa.

5.4 - SIMULAZIONE NUMERICA.

Per calcolare le risposte del velivolo ai comandi prestabiliti si effettua un’integrazione numerica diretta del sistema completo di equazioni differenziali lineari della dinamica del velivolo precedentemente discusse, con la costruzione di un opportuno codice lavorando in ambiente Matlab. Le simulazioni condotte sono di durata pari a 5-10 secondi e l’algoritmo d’integrazione numerica utilizza un passo di integrazione temporale di 0.01 secondi. Dal momento che le manovre analizzate sono effettuate in corrispondenza di in una generica condizione di trim a partire dalla quale si valutano le risposte temporali del velivolo, le condizioni iniziali di tutte le variabili di stato in gioco sono assunte nulle.

5.5 - MOMENTI DI INERZIA DEL VELIVOLO.

Le componenti del tensore di inerzia del velivolo relative alle tre differenti condizioni di peso sono valutati in una terna assi stabilità a partire dai corrispondenti valori noti in assi corpo, secondo le diverse combinazioni di carico pagante e combustibile imbarcati. Ciò richiede una rotazione del tensore d’inerzia riferito ad una terna assi corpo pari all’angolo

w

α compreso tra gli assi X_B ed X_S , essendo α_w come illustrato in precedenza nella figura 2.1 l’angolo individuato tra la direzione del flusso asintotico che investe il sistema ala-fusoliera e l’asse X . Definiti: T la matrice di trasformazione, T e il tensore d’inerzia rispettivamente in assi stabilità ed in assi corpo, tra questi vale la relazione che segue: B R S TB 1 − ⋅ ⋅ = _{R B R} S T T T T dove:           − = w w w w R T α α α α cos 0 sin 0 1 0 sin 0 cos

Nelle tabelle 5.11, 5.12, 5.13 sono indicati i valori delle componenti del tensore d’inerzia per i tre pesi del velivolo considerati comuni a tutte le condizioni di volo prese in esame. B T PESO VELIVOLO [Lb]: W =48500 X I 1.75 105 Y I 7.80 105 Z I 8.80 105 COMPONENTI TENSORE DI INERZIA IN ASSI CORPO [Slug Ft2]

XZ

I 0.70 105

Tab. 5.7: Componenti del tensore d’inerzia in assi corpo per un peso di 48500 Lb.

SO VELIVOLO [Lb]: W =66400 X I 2.00 105 Y I 9.00 105 Z I 10.30 105 COMPONENTI TENSORE DI INERZIA IN ASSI CORPO [Slug Ft2_]

XZ

I 0.70 105

Tab. 5.8: Componenti del tensore d’inerzia in assi corpo per un peso di 66400 Lb.

PESO VELIVOLO [Lb]: W =77700 X I 2.56 105 Y I 9.01 105 Z I 10.86 105 COMPONENTI TENSORE DI INERZIA IN ASSI CORPO [Slug Ft2]

XZ

I 0.70 105

5.6 - DERIVATE AERODINAMICHE DEL VELIVOLO.

Le derivate aerodinamiche da ricostruire per il calcolo delle risposte temporali del velivolo secondo il modello della dinamica a tre gradi di libertà sono le seguenti:

( )

D u C W SV X =−ρ _w

( )

C_L W SV X 2 ρ =

( )

L u C W SV Z =−ρ _w

(

C _L C _D

)

W SV Z = − ρ _α + 2 q W

( )

CLq c SV Z 4 ρ − =

( )

α ρ & & L w C W c S Z 4 − = _e

(

C_Le

)

W SV Z_δ ρ _δ 2 2 − =

(

Mu

)

u f C M = ρ

(

_Mα

)

Y w C I c SV M 2 =

( )

_Mq Y q C I c SV M 4 2 ρ =

(

_α

)

ρ & & M Y w _I C c S M 4 2 =

(

_Me

)

Y e _I C c SV M_δ ρ _δ 4 2 =

Le dimensioni delle derivate sono tali da fornire, rispettivamente per quelle in Z ed in

M , forze divise per il peso del velivolo oppure coppie divise per il momento d’inerzia del velivolo rispetto all’asse Y se moltiplicate per la variabile di stato rispetto alla quale sono state ottenute. Le precedenti derivate aerodinamiche riferite ad una terna assi stabilità risultano essere funzioni oltre che della geometria e delle caratteristiche ponderali del velivolo dei parametri che caratterizzano ciascuna condizione di volo quali: peso,quota e velocità di volo. Inoltre, tutti i coefficienti aerodinamici che caratterizzano le derivate in

S

dipendono fondamentalmente dal numero di mach di volo mentre quelli che influenzano le derivate in M anche dalla posizione del centro di gravità del velivolo.

S

w α

M

C _α&

Le derivate Z e sono implicitamente note, essendo noti sperimentalmente i coefficienti aerodinamici da cui dipendono: C e C riferiti all’intero velivolo. Il valore di è determinabile a partire dai valori sperimentali di

w& Zq α& L Lq e Z_δ

(

C_Lα

)

∗_tail e e S δ α ∂ ∂ . Risulta infatti:

( )

e C S S e C S S e C S S C S tail L t S S tail L t tail L t e L _δ α δ α α δ α δ _∂ ∂ = ∂ ∂ ∂ ∂ = ∂ ∂ = ∗

Il valore del coefficiente così valutato deve essere moltiplicato per la superficie di riferimento e per la velocità V del velivolo al fine di ottenere la cercata in quanto il

include l’effetto della variazione della velocità del flusso che investe la coda rispetto a quello asintotico indisturbato.

e Z_δ

(

)

∗ tail L C _α

Per la derivata Z occorre determinare il coefficiente C riferito all’intero velivolo: derivando rispetto all’angolo d’incidenza dell’ala

w Lα

w

α la portanza complessiva data dal contributo fornito dall’ala e dalla coda, esplicitato quest’ultimo proprio in funzione dell’angolo stesso, si ottiene la seguente espressione:

(

) (

)

S S C C C t w tail L wb L Lα = α + α ∗ 1−εα

La pendenza della curva di portanza del sistema ala-fusoliera C si determina dalle curve sperimentali C

wb Lα

(

_w

Lwb = f α

)

. Si è già discusso circa la pendenza della curva di

portanza della coda orizzontale nel paragrafo 4.5.

Per calcolare le derivate M ed sfruttando i coefficienti aerodinamici sperimentali ,

(

riferiti all’intero velivolo con una posizione del baricentro coincidente con il punto individuato sull’asse longitudinale di fusoliera corrispondente al 25 % della corda media aerodinamica dell’ala misurato a partire dal bordo d’attacco della stessa, occorre valutare i contributi forniti singolarmente dal sistema ala-corpo e dalla sola coda orizzontale al valore complessivo dei coefficienti aerodinamici C , . Calcolando i

q Mw&

( )

A

Mq

C _0.25

)

₀A_.25

Xa Xt− Xt Xa CG 0.25 mac 0.25 mac

Fig. 5.5: Parametri geometrici dell’ala e della coda orizzontale del velivolo.

contributi al momento rispetto al centro di gravità del velivolo forniti dalle singole componenti e dipendenti dalla posizione del baricentro stesso, ne derivano per i coefficienti suddetti le seguenti espressioni (figura 5.5):

( )

( )

( )

_   +     + = S S c Xa C c Xa C C C t tail Lq wb Lq A Mq Mq _0.25

(

)

(

)

+_

(

)

_     + = S S c Xa C c Xa C C C t tail L wb L A M

Mα& α& 0.25 α& α&

Per il coefficiente aerodinamico C da cui dipende la derivata M vale la seguente

considerazione. L’incremento di momento picchiante dovuto alla rotazione

e

dell’equilibratore è funzione dell’incremento della portanza

( )

L_{tail δe} e della coppia aerodinamica

(

M_tail

)

_δe agenti sulla coda e generatisi in seguito alla deflessione δe

dell’equilibratore, pensati applicati in corrispondenza della proiezione sull’asse longitudinale di fusoliera del centro aerodinamico della coda orizzontale medesima. La risultante dell’incremento di momento picchiante complessivo espressa in termini di coefficienti aerodinamici, fornisce la relazione necessaria per determinare .

(

M

)

_δe e M C _δ M C_M

)

_tail e M C _δ 0 e M C _δ = Xa C w Lα

( )

w S f α α =

( )

_δe =

(

M_tail

) ( ) (

_δe − L_{tail δe} Xt−Xa

)

Da cui:

(

)

_−_

(

)(

−

)

_   = c Xa Xt C c S c S C t t _Le tail e M e δ δ δ

Per conoscere il valore di C rimane da ricavare il coefficiente aerodinamico relativo alla sola coda

(

: avendo a disposizione i valori sperimentali del

(

relativi all’intero velivolo con baricentro al 25 % della corda media aerodinamica e conoscendo il , sulla base della precedente relazione è possibile determinare il coefficiente cercato ponendo . L’espressione che ne deriva è la seguente:

e Mδ

)

_0.25 e L C _δ

(

)

(

)

(

)

_      +       = t t e L t t e M tail e M c Xt S S C c S c S C _{δ δ} δ 0.25

Il termine M richiede il coefficiente : in analogia a quanto fatto per il C , derivando l’equazione di momento rispetto all’angolo d’incidenza dell’ala ed esprimendo in funzione di quest’ultimo l’angolo d’incidenza della coda (

α

M

C

), ritenendo sempre valida l’ipotesi che gli angoli siano di modesta entità e che siano trascurabili i relativi termini di ordine superiore al primo, si ottiene la seguente relazione:

(

)(

[

)

(

)

]

(

)

      − + − −     = ∗ c Xa Xt S S C C c Xa C C t tail D tail L w wb L Mα α 1 εα α 0

Le derivate X , , possono essere immediatamente calcolate perché legate ai coefficienti di portanza o di resistenza complessiva dell’intero velivolo, entrambi noti.

u Xw Zu

Nel calcolo della X in prima analisi si può assumere trascurabile la variazione del

coefficiente di resistenza del velivolo con l’angolo d’incidenza dell’ala, generalmente indicato con il termine C , rispetto al valore del coefficiente di portanza del velivolo .

w

α

D CL

Infine si può ricostruire la derivata aerodinamica M effettuando a priori una

approssimazione coerente con l’ordine di grandezza che generalmente questa possiede. L’espressione completa della derivata M si può ottenere derivando tutti i contributi

forniti al momento intorno all’asse

u

u

Y del velivolo

(

Y_B ≡Y_S

)

con polo nel centro

aerodinamico dell’ala rispetto alla velocità di volo al trim V : questa risulta avere la seguente forma:

( )

_       ∂ ∂ +         ∂ ∂ = ∂ ∂ = ∗ Ltrim trim Ltrim trim trim V C M C V M V u V C q c S V q C c S V M M , ,

La precedente relazione deriva dall’aver considerato il momento complessivo delle forze aerodinamiche M come funzione della pressione dinamica q e del coefficiente di momento complessivo C il quale a sua volta risulta funzione sostanzialmente della velocità di volo:

M

( )

qSc CM

Il termine _       ∂ ∂ Ltrim trimC V M V C q c ,

S che compare nell’espressione di

( )

M_u ∗, ed in particolare la

variazione

V C_M ∂ ∂

, dipende dalle variazioni nell’intorno della condizione d’equilibrio con la velocità ovvero con il numero di mach per condizioni di volo a quota costante, delle seguenti quantità: 1- il coefficiente di portanza della coda orizzontale; 2- il coefficiente di momento aerodinamico del sistema ala-corpo, intorno al relativo centro aerodinamico; 3- la forza propulsiva: 1:

(

( )

)

V C_L trim_tail ∂ ∂ 2:

(

(

)

)

V C_M trim_wb ∂ ∂ _0.25 3:

(

( )

)

V T_eng trim ∂ ∂ ovvero: 1:

(

( )

)

M C_L trim_tail ∂ ∂ 2:

(

(

)

)

M C_M trim_wb ∂ ∂ _0.25 3:

(

( )

)

M T_eng trim ∂ ∂

Nelle figure 5.6 - 5.10 sono rappresentate per alcune condizioni di volo le curve equilibrate in funzione del mach relative rispettivamente al coefficiente di portanza della coda orizzontale, alla spinta propulsiva ed al coefficiente di momento aerodinamico del sistema ala-corpo: •

( )

C trim f

( )

M tail L = •

( )

T trim f(M) eng =

(

C

)

f

( )

M triem wb M0.25 = •

(

C_M0.25

)

triem_wb = f

(

M

)

L’analisi degli andamenti delle curve citate consente di ritenere in prima analisi che il contributo apportato dalle singole variazioni

(

( )

)

V C_L trim_tail ∂ ∂ ,

(

(

)

)

V C_M trim_wb ∂ ∂ _0.25 ,

(

( )

)

V T_eng trim ∂ ∂ alla variazione complessiva V C_M ∂ ∂

sia di modesta entità quindi si ritiene accettabile trascurare nella espressione della derivata aerodinamica

( )

M_u ∗ il termine dipendente dalla

V C_M ∂ ∂

rispetto alla quantità _

      ∂ ∂ Ltrim trimC V M V q C c S ,

. In conclusione quindi, per il calcolo della

( )

M_u ∗

si assume che il termine che tiene conto della variazione della sola pressione dinamica con la velocità di volo sia quello preponderante.

Inoltre per un propulsore a getto, potendo generalmente ritenere la spinta T indipendente

dalla velocità di volo almeno in intervalli sufficientemente ampi nell’intorno della velocità di trim, il termine eng

( )

(

)

V T trim eng ∂ ∂

)

∗ u M

può considerarsi sempre nullo [14]. Dunque l’espressione finale adottata per la

(

dalla quale si ottiene la derivata M_u cercata è la seguente:

( )

_       ∂ ∂ = ∗ Ltrim trimC V M u V q C c S M , → 

( )

Y u u I M M ∗ =

Fig. 5.6: Curve

( )

C_L trim_tail = f

(

M

)

nelle condizioni indicate per un peso di 48500 Lb.

Fig. 5.8: Curve

( )

C trim f

(

M

tail

L =

)

nelle condizioni indicate per un peso di 77700 Lb.

5.7 - ANALISI DELLE RISPOSTE TEMPORALI DEL VELIVOLO.

La simulazione numerica fornisce le risposte temporali del velivolo che ne caratterizzano la dinamica negli istanti immediatamente successivi l’azionamento del comando. A titolo di esempio nelle figure 5.11 – 5.12 che seguono, per una condizione di volo ad alta velocità ed alta quota sono riportati gli andamenti temporali delle variazioni delle grandezze che descrivono la dinamica del velivolo ottenute mediante il modello di corto periodo con un ingresso d’equilibratore sia a rampa che sinusoidale, avente in entrambi i casi ampiezza pari a 1 [deg]. In particolare si riportano in funzione del tempo:

• Angolo di rotazione della superficie mobile dell’equilibratore δe in [deg].

• Componente di velocità e in [Ft/sec]. w

• Velocità angolare q in [rad/sec]. • Accelerazione angolare q in [rad/sec_& 2_].

• Variazione dell’angolo d’attacco dell’ala ∆α_wb in [deg].

• Variazione dell’angolo d’assetto del velivolo ∆θ in [deg].

• Variazione dell’angolo di pendenza della traiettoria di volo γ in [deg].

• Variazione del fattore di carico ∆n_Z.

Per la condizione di volo analizzata si riscontra che, con una rotazione verso l’alto dell’equilibratore fino al raggiungimento di un’ampiezza massima unitaria facendo seguire all’angolo di deflessione della superficie mobile le due distinte leggi di moto precedentemente discusse nel paragrafo 5.3, il fattore di carico raggiunto dal velivolo è sempre inferiore al valore massimo consentito di 2.5.

Fig. 5.11: Risposte temporali del velivolo al comando a rampa d’equilibratore nelle condizioni indicate.

Fig. 5.12: Risposte temporali del velivolo al comando sinusoidale d’equilibratore nelle condizioni indicate.