2 – Analisi modale del telaio col metodo degli elementi
finiti.
2.1 – Introduzione.
Le analisi agli elementi finiti sono state le prime analisi effettuate in ordine di tempo. Esse hanno permesso di “prendere confidenza” con la struttura, individuando il range di frequenza entro il quale sono contenuti i primi modi propri, e visualizzando le relative forme modali. Nell’ambito di tali analisi sono stati sviluppati diversi modelli per riprodurre il comportamento del telaio, ciascuno con un differente grado di approssimazione. Le fasi principali del loro sviluppo sono state la modellazione solida, la discretizzazione in E.F. e la successiva analisi. La modellazione solida è stata effettuata utilizzando un modellatore solido quale il ProENGINEER; ciò ha permesso di ottenere un modello parametrico del telaio, utile per future analisi di sensibilità. I dati geometrici, necessari per la sua modellazione, sono stati ricavati da un disegno costruttivo del telaio, fornito dalla DUCATI. Rispetto al modello reale, nel modello CAD-3D sono stai trascurati tutti quei particolari quali bulloneria, piastrine di supporto, fermi, ritenuti non influenti sul comportamento dinamico della struttura. Le analisi F.E.M. sono state effettuate col software di calcolo ANSYS; sono state effettuate sia analisi dinamiche con diverse condizioni di vincolo applicate alla struttura, sia analisi di rigidezza. I paragrafi seguenti riportano una breve descrizione dei modelli sviluppati ed i risultati ottenuti.
2.2 – Modello trave.
Il modello trave, nominato Telaio_beam, è stato sviluppato modellando le linee d’asse dei tubi presenti sul telaio. Le coordinate dei punti d’intersezione geometrica delle linee d’asse sono state ricavate graficamente dal disegno costruttivo. In questo modello alcuni particolari del telaio, quali la staffa supporto serbatoio e la piastra supporto chiavistello, sono stati semplificati nella forma, ipotizzando uno sviluppo con sezione costante. Altri particolari quali le maniglie
passeggero, le boccole fissaggio motore e le boccole di fissaggio del bilanciere sopsensione,
ottenuto dal modello CAD-3D. In questa fase non sono stati modellati alcuni piastrini di rinforzo presenti nella zona anteriore, e nella zona della sospensione posteriore. Gli elementi utilizzati nell’analisi F.E.M. sono stati principalmente il PIPE16, usato per i tratti di tubo rettilineo, ed il PIPE18, utilizzato per i tratti curvi. Le dimensioni dei tubi sono state inserite come costanti reali nella definizione dei parametri degli elementi. Per alcuni particolari, quali la
staffa supporto serbatoio e la piastra supporto chiavistello, e per la costruzione dei vincoli
posti alla struttura, sono stati utilizzati degli elementi trave, quali il BEAM8. La discretizzazione in E.F. del modello è stata fatta manualmente introducendo nei tubi “portanti” un numero di nodi sufficiente a riprodurre correttamente le forme modali; i puntoni di collegamento tra i tubi portanti sono stati modellati con un solo nodo interno. Le condizioni di vincolo applicate alla struttura sono state
o incastro sul cannotto, nel modello TELAIO_BEAM_I;
o appoggio sul cannotto e cerniera sulla sospensione posteriore, nel modello
TELAIO_BEAM_A;
o assenza di vincoli, nel modello TELAIO_BEAM_L;
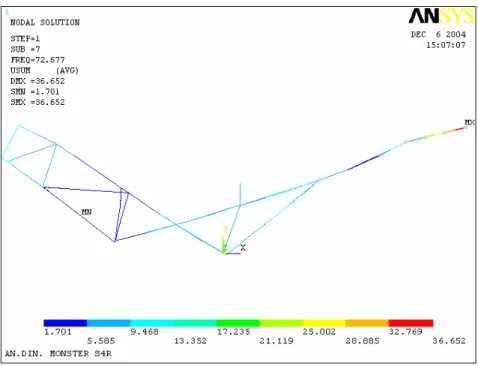
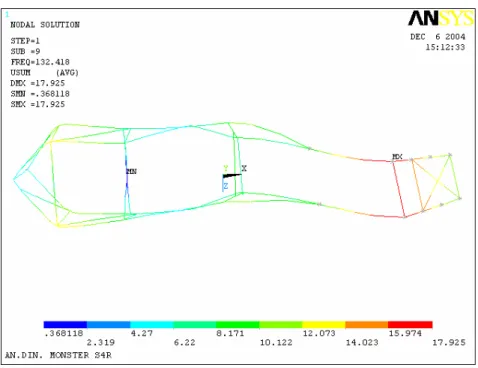
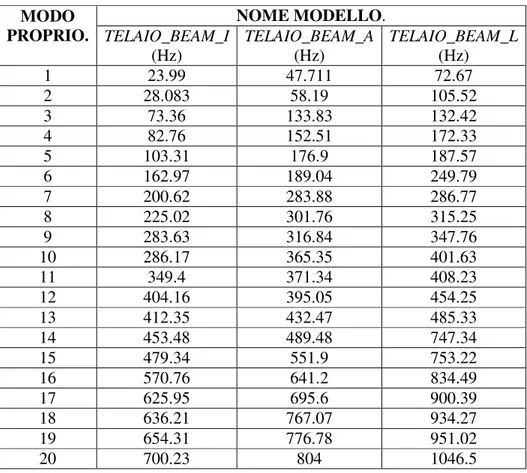
La figura 2.1 mostra un’immagine del modello TELAIO_BEAM_L. La figura 2.2, 2.3, 2.4 mostrano un’immagine dei primi modi propri del telaio, supposto in assenza di vincoli. La tabella 2.1 elenca le frequenze proprie trovate.
Figura 2.4: Terzo modo proprio ad una frequenza di 132.41 Hz.
NOME MODELLO. MODO PROPRIO. TELAIO_BEAM_I (Hz) TELAIO_BEAM_A (Hz) TELAIO_BEAM_L (Hz) 1 23.99 47.711 72.67 2 28.083 58.19 105.52 3 73.36 133.83 132.42 4 82.76 152.51 172.33 5 103.31 176.9 187.57 6 162.97 189.04 249.79 7 200.62 283.88 286.77 8 225.02 301.76 315.25 9 283.63 316.84 347.76 10 286.17 365.35 401.63 11 349.4 371.34 408.23 12 404.16 395.05 454.25 13 412.35 432.47 485.33 14 453.48 489.48 747.34 15 479.34 551.9 753.22 16 570.76 641.2 834.49 17 625.95 695.6 900.39 18 636.21 767.07 934.27 19 654.31 776.78 951.02 20 700.23 804 1046.5
2.3 – Modello guscio.
Il modello guscio ha avuto come obbiettivo la riproduzione del comportamento della superficie media della struttura, permettendo inoltre di modellare particolari quali piastrine di rinforzo,
maniglie passeggero che sono stati trascurati nel modello precedente. La sua modellazione è
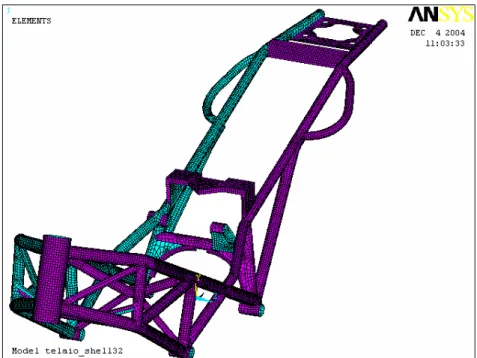
stata effettuata in ambiente ProENGINEER, ed è stato utilizzato il modello trave come scheletro di partenza, lungo il quale estrudere le superfici. Sebbene l’obbiettivo della modellazione era la creazione di superfici, si è preferito usare delle feature di modellazione solida creando dei tubi pieni, di diametro pari al diametro medio dei tubi presenti sul telaio; successivamente con la rimozione del volume interno e l’eliminazione di alcune superfici si è ottenuto il modello voluto. L’uso di feature di modellazione solida, al posto di quelle di modellazione di superfici, ha permesso di ottenere in automatico le superfici di intersezione dei tubi convergenti nei nodi del telaio. La rimozione del volume intermo ha creato dei buchi sulla struttura, rendendo necessaria una successiva operazione di “riparazione” in ambiente F.E.M. La figura 2.6 mostra un’immagine del modello CAD-3D.
Il modello CAD-3D è stato importato direttamente in ambiente ANSYS, dove sono stati rimossi il volume interno e alcune superfici “tappo” non desiderate. L’elemento utilizzato per la sua discretizzazione in E.F: è stato lo SHELL63, un elemento guscio con quattro nodi all’estremità, con sei gradi di libertà per nodo. Il problema principale della discretizzazione è stato quello di rispettare i limiti sulla forma degli elementi, cioè i rapporti b/h, tipicamente compresi tra 1/10<b/h<10, e la loro estensione in senso circonferenziale, in genere minore di quindici gradi al fine di ottenere una buona approssimazione delle superfici curve. La discretizzazione è stata fatta in automatico dal programma, prevedendo sulle linee del modello un’ampiezza degli elementi non superiore a cinque millimetri. Essa è stata controllata solo nelle zone di riparazione del modello dove, per facilitare l’operazione d’inserimento manuale degli elementi, sono state previste delle dimensioni maggiori. Le informazioni relative allo spessore degli elementi sono state introdotte come attributi dell’area su cui si estendono gli elementi. Le condizioni di vincolo applicate alla struttura sono state
o incastro sul cannotto, nel modello TELAIO_SHELL_I;
o appoggio sul cannotto e cerniera sulla sospensione posteriore, nel modello
TELAIO_SHELL_A;
o assenza di vincoli, nel modello TELAIO_SHELL_L;
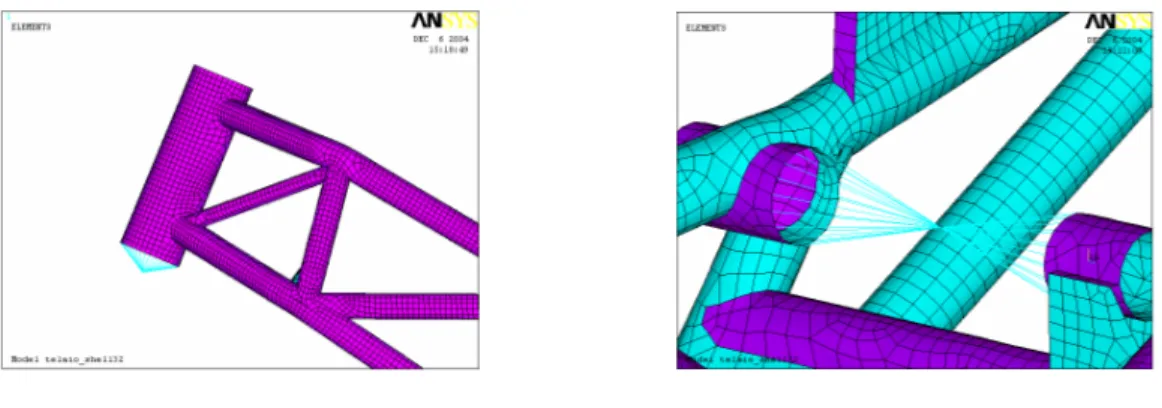
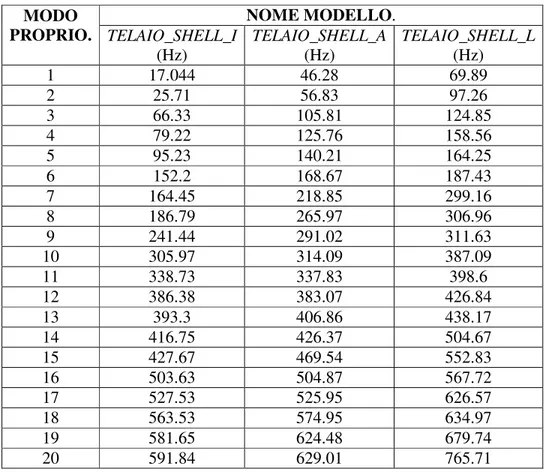
La seconda condizione di vincolo è stata ottenuta con l’utilizzo di elementi trave, BEAM4, disposti in maniera da simulare vincoli puntiformi, lasciando al telaio la libertà di deformarsi anche torsionalmente. La figura 2.7 mostra un’immagine del modello F.E.M.; la figura 2.8 evidenzia l’azione di riparazione manuale effettuata sui tubi, mentre la figura 2.9 mostra i vincoli applicati sul modello TELAIO_SHELL_A. Le figure 2.10 e seguenti mostrano i primi modi propri del modello TELAIO_SHELL, per le diverse condizioni di vincolo analizzate. La tabella 2.2 riporta le frequenze proprie trovate.
Figura 2.6: Modello TELAIO_SHELL.
Figura 2.8: Vincoli creati nel modello TELAIO_SHELL_A.
Figura 2.9: Primo modo proprio del TELAIO_SHELL_I ad una frequenza di 17.04 Hz.
NOME MODELLO. MODO PROPRIO. TELAIO_SHELL_I (Hz) TELAIO_SHELL_A (Hz) TELAIO_SHELL_L (Hz) 1 17.044 46.28 69.89 2 25.71 56.83 97.26 3 66.33 105.81 124.85 4 79.22 125.76 158.56 5 95.23 140.21 164.25 6 152.2 168.67 187.43 7 164.45 218.85 299.16 8 186.79 265.97 306.96 9 241.44 291.02 311.63 10 305.97 314.09 387.09 11 338.73 337.83 398.6 12 386.38 383.07 426.84 13 393.3 406.86 438.17 14 416.75 426.37 504.67 15 427.67 469.54 552.83 16 503.63 504.87 567.72 17 527.53 525.95 626.57 18 563.53 574.95 634.97 19 581.65 624.48 679.74 20 591.84 629.01 765.71
2.4 – Confronto tra il modello trave ed il modello guscio.
Al fine di individuare uno strumento utile per la caratterizzazione del comportamento della struttura sono stati messi a confronto i risultati ottenuti con i due modelli di telaio. I termini secondo i quali è stato eseguito il confronto sono stati:
o riproduzione delle forme modali. o rigidezza flessionale del modello. o peso del modello.
o tempo di calcolo.
Quanto al primo termine del confronto si osserva che la differenza tra i risultati forniti da i due modelli cresce con l’aumentare dell’ordine del modo riprodotto. Si è osservato che il modello guscio riproduce più realisticamente il comportamento della struttura; esso infatti prevede dei modi propri, caratterizzati da vibrazioni locali di parti della struttura, che invece non sono presenti nel modello trave. A parità di modo riprodotto si è osservato che il modello trave “sovrastima” la corrispondente pulsazione di un valore crescente col crescere del modo proprio. Quanto alla rigidezza flessionale prevista dai due modelli, essa è stata calcolata ponendo dei vincoli d’incastro sul cannotto e dei carchi verticali all’estremità opposta del telaio. I carichi sono stati introdotti come forze applicati ai nodi della zona d’estremità per un valore complessivo di 500 N. Gli spostamenti calcolati dai due modelli sono stati di:
Modello trave : 15.69 mm. Modello guscio : 18.14 mm.
ottenendo una rigidezza flessionale di: Modello trave : 31.86 N/mm
Modello guscio : 27.56 N/mm
La massa della struttura riprodotta dai due modelli è di: Modello trave : 10.579 Kg.
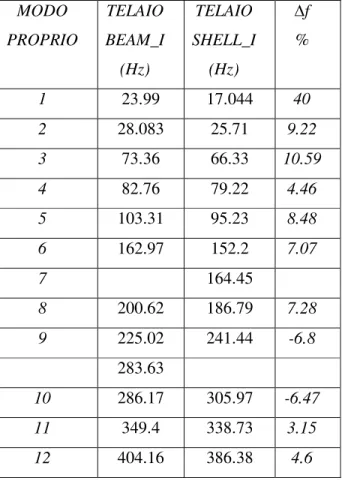
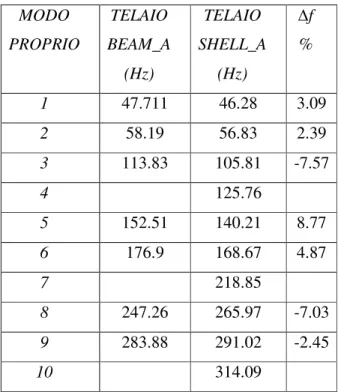
con il modello trave più pesante del modello guscio in quanto non considera la reale geometria dell’intersezione tra i tubi. Tali valori mostrano un buon accordo con il valore di 11 Kg, dichiarato come dato costruttivo del telaio. Inoltre il rapporto (K/M), maggiore per il modello trave, spiega, almeno per i primi modi, la differenza tra i valori delle frequenze di risonanza. Un ultimo ma non meno importante termine di confronto è costituito dal tempo di calcolo richiesto per i due modelli che varia da qualche minuto per il modello trave a diverse ore per il modello guscio. Considerando anche il tempo necessario per la loro modellazione si può concludere che, per una analisi sommaria, e limitata ai primi modi propri, il modello trave costituisce uno strumento versatile. Le tabella 2.3, 2.4, 2.5 riassumono i parametri di tale confronto.
MODO PROPRIO TELAIO BEAM_I (Hz) TELAIO SHELL_I (Hz) f % 1 23.99 17.044 40 2 28.083 25.71 9.22 3 73.36 66.33 10.59 4 82.76 79.22 4.46 5 103.31 95.23 8.48 6 162.97 152.2 7.07 7 164.45 8 200.62 186.79 7.28 9 225.02 241.44 -6.8 283.63 10 286.17 305.97 -6.47 11 349.4 338.73 3.15 12 404.16 386.38 4.6
MODO PROPRIO TELAIO BEAM_A (Hz) TELAIO SHELL_A (Hz) f % 1 47.711 46.28 3.09 2 58.19 56.83 2.39 3 113.83 105.81 -7.57 4 125.76 5 152.51 140.21 8.77 6 176.9 168.67 4.87 7 218.85 8 247.26 265.97 -7.03 9 283.88 291.02 -2.45 10 314.09
MODO PROPRIO TELAIO BEAM_L (Hz) TELAIO SHELL_L (Hz) f % 1 72.67 69.89 4.1 2 105.52 97.26 8.49 3 132.42 124.85 6 4 172.33 158.56 8.6 5 164.25 6 187.57 187.43 0.074 7 249.79 299.16 -16.5 8 286.77 306.96 -6.5 9 315.25 311.63 1.1 10 387.09 347.76 11 401.63 398.6 0.76 12 408.23 426.84 -4.35
Tabella 2.5: Confronto tra i modelli trave e guscio, nella condizione di telaio libero.
CARATTERISTICHE DEI MODELLI. Num. Elementi 119 27512
Rigidezza flessionale 31.86 kN/mm 27.56 kN/mm 29.051 kN/mm (dato sperimentale) Peso 10.579 kg 10.257 kg 11 kg
(dato costruttivo.) Rapp. K/M 1.73 rad/s 1.639 ra/7s 1.62 Tempo di calcolo. 10 minuti 3 ore
2.4 - Descrizione dei modi propri del telaio.
Si analizzano di seguito le forme modali dei primi dieci modi propri del telaio, specificando il tipo di modo, il numero e la posizione dei nodi. La configurazione scelta è quella di struttura libera in assenza di vincoli.
1. (69.89 Hz): è un’oscillazione flessionale nel piano longitudinale del telaio.
La struttura si inflette presentando due nodi interni in corrispondenza delle boccole motore anteriori e dell’intersezione tra i montanti posteriori
2. (97.26 Hz): è un’oscillazione torsionale che interessa principalmente la
parte posteriore del telaio, con un nodo interno nella zona di collegamento tra i montanti superiori anteriori, e la parte anteriore quasi indeformata. 3. (124.85 Hz): è un oscillazione torsionale simile alla precedente, con un
nodo interno in corrispondenza delle traversa della sospensione posteriore, con la parte anteriore che oscilla in opposizione alla posteriore.
4. (158.56 Hz): è un’oscillazione flessionale nel piano longitudinale del telaio.
Sono presenti tre nodi interni situati rispettivamente, nella zona di collegamento tra i montanti inferiori anteriori, nella zona della sospensione posteriore, e in corrispondenza della piastra di supporto del chiavistello. 5. (164.25 Hz): è un’oscillazione torsionale con due nodi interni situati in
corrispondenza dell’intersezione tra i montanti anteriori e posteriori e in prossimità della piastra di supporta del chiavistello. Per effetto di questa deformazione si ha uno scorrimento longitudinale della parte anteriore rispetto al piano di simmetria.
6. (187.43 Hz): è un’oscillazione torsionale simile ala precedente ma con uno
scorrimento più marcato. Per effetto di tale deformazione la struttura si flette anche nel piano trasversale, con una deformata che presenta tre nodi interni, situati rispettivamente nella zona di collegamento tra i montanti inferiori anteriori, nella zona della sospensione posteriore e nella zona della piastra di fissaggio portatarga.
7. (299.15 Hz): è un oscillazione torsionale con tre nodi interni situati
rispettivamente nella zona di collegamento tra i montanti superiori anteriori, nella zona della sospensione posteriore, e nella zona della piastra di fissaggio portatarga. Per effetto di tale deformazione, la struttura si
nodi interni, situati rispettivamente nella zona di collegamento tra i montanti inferiori anteriori, nella zona della sospensione posteriore, nella zona d’intersezione tra i montanti posteriori e nella zona della piastra di fissaggio portatarga.
8. (306.95 Hz): è un’oscillazione flessionale nel piano trasversale che
interessa principalmente la parte posteriore. I montanti posteriori oscillano in opposizione creando un effetto “polmone”, con una deformata che presenta una cresta in corrispondenza della loro intersezione.
9. (311.62 Hz): è un’oscillazione flessionale nel piano trasversale con un nodo
d’estremità in corrispondenza del cannotto e due nodi interni situati rispettivamente nella zona della sospensione posteriore e nella zona della piastra di supporto del chiavistello. Rispetto al piano di simmetria la parte anteriore oscilla in fase, mentre quella posteriore in opposizione.
10. (387.09 Hz): è un’oscillazione flessionale nel piano longitudinale con
quattro nodi interni situati rispettivamente nella zona di collegamento tra i montanti inferiori,nella zona della sospensione posteriore, nella zona d’intersezione tra i montanti posteriori e nella zona della piastra portatarga.
Figura 2.12: Secondo modo proprio del TELAIO_SHELL_L.
Figura 2.14: Terzo modo proprio del TELAIO_SHELL_L, vista in pianta.
Figura 2.16: Quinto modo proprio del TELAIO_SHELL_L.
Figura 2.18: Sesto modo proprio del TELAIO_SHELL_L, vista in pianta.
Figura 2.19: Settimo modo proprio del TELAIO_SHELL_L, vista in pianta.
Figura 2.21: Nono modo proprio del TELAIO_SHELL_L.