28
Capitolo 4
Analisi del problema aeroelastico
4.1 Introduzione
Aeroelasticità è il termine usato per parlare della disciplina che tratta dell’interazione fra la deformazione di una struttura elastica, posta in un flusso, e le risultanti forze aerodinamiche. La sua natura interdisciplinare è bene illustrata dalla fig. 4.1, di seguito riportata, la quale mostra l’interazione fra le tre discipline aerodinamica, dinamica ed elasticità [7];
Fig. 4.1Scema delle discipline che comprende l’aeroelasticità
L’aerodinamica classica fornisce una predizione delle forze su un corpo, considerato rigido, di forma assegnata. La teoria dell’elasticità ci dice come un corpo elastico si deforma in seguito all’applicazione su esso di un carico esterno. La dinamica introduce gli effetti inerziali.
29
Nell’aeroelasticità si vede che i carichi dipendono dalla deformazione della struttura e che la deformazione della struttura dipende dai carichi aerodinamici applicati: siamo di fronte ad un problema accoppiato.
Fenomeni aeroelastici, come la divergenza torsionale delle ali, furono oggetto di studi accurati negli anni ‘30 del secolo scorso quando la struttura classica di biplano fu sostituita da quella a monoplano con struttura metallica. Questo per fornire adeguata rigidezza torsionale al monoplano.
Durante la prima guerra mondiale si manifestarono diversi incidenti catastrofici dovuti a problemi di instabilità dinamica nota con il nome di Flutter e da quel punto in poi il Flutter divenne uno degli argomenti principali a cui dare attenzione nella progettazione dei più moderni velivoli.
Un altro argomento da trattare con molta attenzione in fase di progetto, relativo ad un problema di aeroelasticità statica, è l’efficacia dell’alettone. Infatti, all’aumentare della velocità di volo, la rigidezza torsionale dell’ala può essere tale da non sopportare le deformazioni indotte dai carichi aerodinamici e l’alettone può perdere la sua funzionalità o addirittura può esserci l’inversione dei comandi.
Nel progetto di velivoli aerospaziali, i fenomeni aeroelastici possono classificarsi in un ampio range di comportamenti. Si parte da conseguenze che possono portare semplicemente alla sconfortevolezza del volo, per via di rumori e vibrazioni, a fenomeni che possono essere più critici per la resistenza a fatica del velivolo, fino a fenomeni che possono arrivare a condurre la struttura a rotture catastrofiche con l’inevitabile perdita di vite umane.
Oggigiorno, la richiesta principale, nel progetto di velivoli, risiede nel realizzare una struttura la più leggera possibile, sia per ridurre i consumi, sia per far fronte alle stringenti normative relative all’inquinamento ambientale. Una struttura leggera significa altamente deformabile e per questo molto soggetta ai fenomeni aeroelastici.
I fenomeni aeroelastici giocano un ruolo fondamentale anche nella progettazione di turbomacchine e nella realizzazione dei moderni generatoli eolici.
I problemi che più comunemente si trovano ad affrontare gli ingegneri aeroelastici sono quelli relativi alla stabilità della struttura. Benché il modulo elastico di una struttura sia indipendente dalla velocità del velivolo, le forze aerodinamiche dipendono fortemente da esso, perché dipendono da come e quanto si deforma la struttura sotto l’azione dei carichi aerodinamici stessi.
30
Quando le forze d’inerzia hanno entità trascurabile stiamo trattando problemi di aeroelasticità statica come la “Divergenza torsionale”, quando non sono trascurabili trattiamo problemi di aeroelasticità dinamica come il “Flutter”. Entrambi i fenomeni prima riportati possono essere catastrofici. E’ di vitale importanza per il progettista studiare configurazioni alari che vadano esenti da tali problematiche.
Inoltre, l’aeroelasticità studia la risposta della struttura dei velivoli. L’aeroelasticità statica si occupa di quei problemi in cui le forze d’inerzia non contribuiscono come la ridistribuzione della portanza su un’ala posta ad uno specifico angolo d’incidenza rispetto al flusso indisturbato, oppure come la stima del fattore di carico massimo che un aereo può sopportare. I problemi relativi all’inversione dei comandi di alettone vanno sotto tale categoria.
Quando il contributo delle forze d’inerzia non è trascurabile, si vuole sapere come l’aereo reagisce in turbolenza o se incontra una raffica. Un altro importante fenomeno è il Buffeting: vibrazioni indotte dalla scia del flusso dietro le ali. Tale fenomeno affligge i piani di coda dei velivoli.
Tutte queste problematiche sono trattabili nel campo dell’analisi lineare. I problemi di instabilità sono studiabili analizzando le soluzioni non banali del problema omogeneo che descrive il moto (risoluzione dell’equazione caratteristica nel capitolo 3). I problemi di risposta si rifanno alla soluzione dell’equazione non omogenea.
31
4.2 Aeroelasticità statica
Il campo dell’aeroelasticità statica si occupa di tutti quei fenomeni associati all’interazione fra i carichi aerodinamici indotti da un flusso stazionario e le risultanti deformazioni elastiche strutturali delle superfici portanti della struttura. Questi fenomeni sono caratterizzati dall’essere insensibili alle velocità e alle accelerazioni relative alle deformazioni strutturali. Ci sono due tipologie di problemi di progetto. La prima, la quale è anche la più comune a tutti i velivoli, è lo studio degli effetti che hanno le deformazione elastiche della struttura sui carichi aerodinamici che le hanno prodotte rispetto alle condizioni di struttura rigida. Tali effetti hanno conseguenze importanti sulle prestazioni, sulla stabilità del volo e sulla distribuzione dei carichi sulle superfici portanti. La seconda è relativa ai fenomeni d’instabilità statica che sono identificati con il termine di “Divergenza torsionale” e tale classe di problemi può limitare l’inviluppo di volo di un velivolo.
Di seguito si illustrano alcuni di questi fenomeni relativi all’aeroelasticità statica per problemi piuttosto semplici dal punto di vista matematico, ma che sono in grado di mettere in luce i concetti basilari della questione.
Per primo si considera un modello rigido bidimensionale il cui unico grado di libertà consiste nella rotazione attorno all’asse di beccheggio. Tale struttura è vincolata elasticamente con molla torsionale per esprime il problema della “Divergenza Torsionale” . I modelli sono riportati nelle figure seguenti [7]:
32
La rigidezza torsionale del supporto è definita dalla costante k . Scriviamo l’equilibrio al momento rispetto al punto o in cui è incernierato il modello. Assumiamo l’angolo d’incidenza (α) sufficientemente piccolo da poter porre sin α = α e cos α=1.
L’angolo d’incidenza (α) può essere scomposto in una parte relativa ad un struttura rigida torsionalmente anche nel supporto αr e una parte elastica che dipende dall’elasticità del
supporto θ.
Per quanto riguarda la portanza relativa ad una struttura completamente rigida Lr può essere
ricavato il seguente valore:
mentre la portanza considerando il supporto elastico torsionalmente è data dalla seguente equazione:
dove q è la pressione dinamica e S è la superficie in pianta dell’ala e Clα è la pendenza della
curva di portanza che data la linearità dell’aerodinamica, ipotizzata, è costante. Bisogna notare che L>Lr per θ>0. Esprimiamo il momento delle forze aerodinamiche Mac
rispetto al centro aerodinamico dell’ala xac:
33
Si sostituiscono le eq. 4.4 e l’eq. 4.3 nell’eq. 4.1 e ricaviamo la rotazione torsionale dell’ala θ legata al’elasticità del vincolo torsionale:
Quando la cerniera “o” è dietro il centro aerodinamico “ac”, in sostanza quando xo>xcg vedi
grafico fig. 4.2, il denominatore dell’eq. 4.5 può annullarsi il che significa che la deflessione elastica torsionale θ può raggiungere valori infiniti incompatibili con la resistenza strutturale torsionale dell’ala. Questo fenomeno di instabilità statico è chiamato nell’aeroelasticità statica “Divergenza torsionale”. La pressione dinamica qD a cui la Divergenza torsionale avviene si
trova ponendo uguale a zero il denominatore dell’eq. 4.5;
La velocità U∞ a cui la divergenza avviene è di sotto riportata:
Quando il centro aerodinamico “ac” è posteriore a “o” al limite coincidente con la cerniera “o”, (asse elastico della struttura), la divergenza torsionale non avviene.
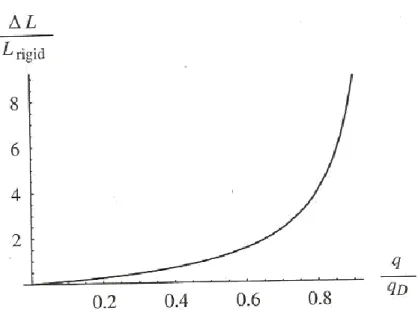
Si riporta di seguito un grafico che mette in evidenza come varia la portanza agente sull’ala elastica torsionalmente, rispetto al caso di ala completamente rigida, in funzione della pressione dinamica a cui il velivolo si trova ad operare [7];
34
Fig. 4.3 Aumento di portanza rispetto al caso rigido in funzione della pressione dinamica q
Bisogna dire che ci sono delle limitazioni a questo modello in quanto ad un certo punto l’ala stallerà e ci sarà un decremento brusco della portanza, tuttavia qualitativamente i risultati prima ottenuti sono veritieri. Inoltre, la struttura può tollerare solo un certo range di deformazione torsionale θ, dopo il quale la struttura cederà.
35
4.2.1 Ala diritta uniforme
Fino ad ora si è focalizzata l’attenzione nell’analizzare ali rigide incernierate con vincoli elastici (molle torsionali). Queste idealizzazioni del problema danno informazioni sulla stabilità e sulla risposta della struttura nel campo dell’aeroelasticità statica, ma per avere informazioni più dettagliate bisogna considerare l’ala come tutta elastica e non rigida.
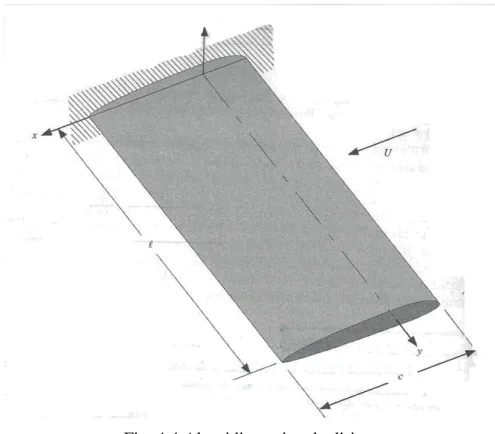
Si tratta, ora il problema di un’ala diritta flessibile incastrata alla radice, la cui struttura è ipotizzata semplificata. Riportiamo nelle figure seguenti i modelli [7];
Fig. 4.4 Ala tridimensionale diritta
L’ala è considerata come una trave incastrata alla radice e libera all’estremità finale. L’asse y è ipotizzato coincidente con l’asse elastico della struttura. L’asse elastico è il luogo di tutti i centri di taglio della struttura. Il centro di taglio di un profilo è quel punto tale che se sul quale viene applicata una forza la sezione non ruota rispetto a quel punto.
La rotazione di ogni sezione trasversale rispetto all’asse elastico, dovuta all’applicazione di un momento torcente rispetto all’asse elastico, provoca un ridistribuzione dei carichi sull’ala.
36
Si scrive l’equilibrio alla rotazione rispetto all’asse elastico per la generica sezione trasversale dell’ala (trave):
M’ac e L’ sono espresse per unità di apertura dell’ala. M’ è positivo quando genera un
momento a cabrare dell’ala, mg è il peso per unità di apertura alare e N è il fattore di carico.
Ora, l’equazione, proveniente dalla teoria di De S.V., che definisce l’equilibrio statico alla rotazione torsionale θ, attorno all’asse elastico, per una struttura deformabile elasticamente, è di seguito riportata:
T è il momento torcente applicato alla generica sezione della trave rispetto all’asse elastico e GJ è la rigidezza torsionale della trave. Si ipotizza che la variazione di momento torcente
lungo l’apertura alare sia proprio il momento per unità di apertura alare definito nell’eq. 4.5 cambiato di segno.
Derivando, dunque, l’eq. 4.8 rispetto ala coordinata y, relativa all’apertura alare, e uguagliandola all’eq. 4.5 si ottiene, operando anche altre sostituzioni, la seguente relazione di equilibrio [7] :
37
Si assume la seguente relazione per la stima del coefficiente locale di portanza Cl:
Con a si definisce la pendenza della curva di portanza, costante lungo tutta l’apertura alare. Si assume che l’angolo d’incidenza dell’ala α(y) sia scomponibile in due contributi, uno relativo alla rotazione dell’ala come corpo rigido αr e l’altro dovuto alla rotazione θ dell’ala
elastica, sottoposta a momento torcente dalle forze aerodinamiche su essa agenti;
Si ottiene, così, l’espressione generale per definire lo stato di equilibrio della struttura deformabile elasticamente in torsione [7]:
In fine per una completa formulazione di questo problema di equilibrio bisogna specificare le condizioni al contorno, sia al lato incastrato dove la rotazione θ=0, sia al lato libero dove il momento torcente è uguale a zero
Si analizza il problema dell’instabilità relativa alla “Divergenza torsionale “ dell’ala flessibile. Si adottano le seguenti definizioni e si riscrive il problema di equilibrio prima trattato dall’eq. 4.12 con le relative condizioni al contorno:
38
I termini prima definiti, e sono indipendenti dalla coordinata y in apertura ala, perché la trave è uniforme.
L’eq. 4.12, che definisce l’equilibrio statico aeroelastico può essere riscritta nella seguente forma:
La soluzione generale della precedente eq. 4.15 è di seguito riportata:
Si applicano le condizioni al contorno di rotazione nulla alla radice e momento torcente nullo all’estremità dell’ala che si traducono rispettivamente nelle seguenti relazioni:
La soluzione per la rotazione elastica θ(y) assume la seguente forma:
Adesso, si può ricavare la distribuzione di portanza L’[N/m] in apertura alare in funzione dell’angolo rigido d’incidenza αr, costante in apertura alare, e in funzione dell’angolo di
torsione dell’ala θ(y).
39
Dall’equazione di equilibrio, eq. 4.19, si nota che per φL=π/2 l’angolo di rotazione in torsione θ(y) diventa infinito. Tale fenomeno si chiama “Divergenza Torsionale” e di pende dal valore di φ precedentemente definito nell’eq. 4.13:
C’è un valore della pressione dinamica q tale che φL=π/2 e questo valore si chiama pressione dinamica di divergenza qD, la cui espressione è riportata sotto:
Si riporta di seguito un grafico, fig 4.3, che mette in evidenza come il fenomeno della divergenza torsionale possa provocare problemi d’instabilità aeroelastica statica della struttura anche per pressioni dinamiche inferiori a quella di divergenza [7]:
40
Se l’asse elastico è davanti alla retta luogo dei centri aerodinamici dell’ala il fenomeno della divergenza torsionale non avviene.
L’eq. 4.20 dice come la portanza si distribuisce in apertura e la fig. 4.4 seguente mette a confronto la distribuzione di portanza di un’ala rigida incastrata, fissato αr, con un’ala elastica
sempre incastrata alla radice, con stesso αr fissato [7]:
41
4.2.2 Ala a freccia uniforme
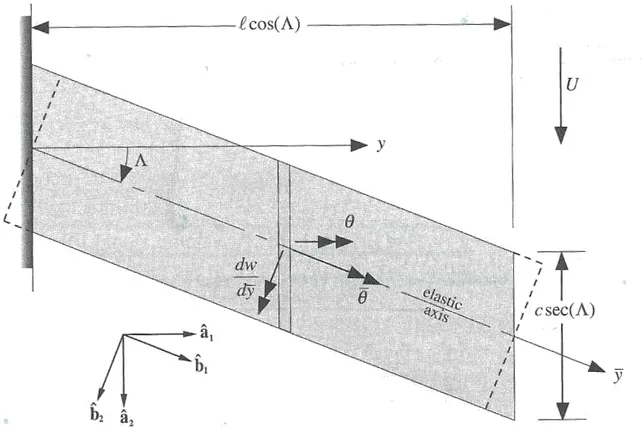
Si osservano ora gli effetti, sui fenomeni aeroelastici statici, che produce il realizzare un’ala a freccia rispetto all’ala diritta. Riportiamo un esempio di ala a freccia nella fig. 4.5 qui sotto rappresentata [7]:
Fig. 4.7 Ala a freccia positiva Λ>0
Le reazioni aerodinamiche dipendono dall’angolo d’incidenza α(y) misurato rispetto alla direzione del flusso indisturbato U∞:
La variazione di incidenza θ(y) dovuta alla torsione elastica dell’ala viene espressa qui in funzione della componete di torsione del asse elastico dell’ala a freccia , vedi fig. 4.5, e in
42
funzione della flessione dell’ala attorno all’asse normale all’asse elastico dell’ala a freccia. Con w si identifica lo spostamento trasversale della trave nel piano .
Il valore della rotazione θ(y), precedentemente definito e rappresentato in fig. 4.5, viene espresso di seguito in funzione dell’angolo di freccia Λ [7]:
Da questa relazione si nota come l’angolo d’incidenza α(y), prima definito nell’eq. 4.24, sia alterato dai fenomeni flessionali dell’ala. L’accoppiamento fra torsione e flessione dell’ala produce effetti che affliggono la risposta aeroelastica statica della struttura in volo e influenzano, di conseguenza, le condizioni in presenza delle quali si ha il manifestarsi del fenomeno d’instabilità statico chiamato “Divergenza torsionale”.
Per determinare la deformazione elastica della struttura due equazioni devono essere formulate; una che tratta l’equilibrio torsionale dell’ala a freccia, rispetto all’asse elastico, e l’altra che tratta l’equilibrio flessionale rispetto all’asse normale all’asse elastico.
Si riportano qui di seguito tali equazioni [7]:
Con pendenza della curva di portanza del generico profilo alare nel caso di ala a freccia. Rielaborando le eq. 4.26, 4.27 grazie all’ eq. 4.24, 4.25 si ricava la forma definitiva del problema dell’equilibrio dell’ala a freccia incastrata con le sue condizioni al contorno.
43
Si riporta qui di sotto le equazioni e le relative condizioni al contorno [7]:
Alla radice l’ala è incastrata e presenta le seguenti condizioni al contorno:
All’estremità libera l’ala presenta momento torcente uguale a zero, momento flettente uguale a zero e taglio uguale a zero e ciò si traduce nelle seguenti condizioni al contorno:
44
L’accoppiamento torsione-flessione è rappresentato dalla presenza del termine w nell’equazione di equilibrio della torsione e del termine nell’equazione di equilibrio alla flessione.
Un caso interessante da esaminare è quando l’asse elastico coincide con l’asse luogo dei centri aerodinamici dell’ala, questo si traduce nel porre e=0, che equivale a dire che l’ala non è soggetta a divergenza torsionale ma può essere soggetta a divergenza flessionale.
La relazione, eq. 4.28 si semplifica, la pressione dinamica di divergenza torsionale qD può
essere ricavata dalla soluzione dell’eq. 4.28. Tale soluzione è qui sotto riportata:
Il meno indica che tale divergenza flessionale ha luogo solo per ali con freccia rivolta in avanti, rispetto ala direzione del moto del velivolo, per le quali Λ < 0.
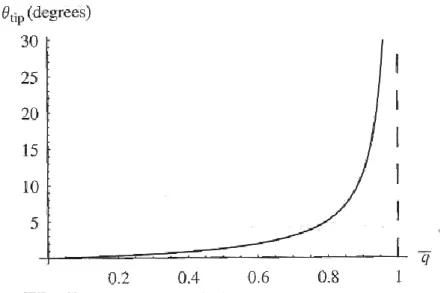
L’accoppiamento degli effetti torsionali e flessionali influenzano nel caso dell’ala a freccia, ora esaminato, sia il fenomeno della divergenza sia la distribuzione dei carichi in apertura. L’effetto globale della freccia dipende fortemente se la freccia è rivolta in avanti (Λ > 0) o rivolta indietro (Λ < 0). Si riporta di seguita un grafico che ne illustra il fenomeno [7]:
Fig.4.8 Pressione dinamica di divergenza in relazione all’angolo di freccia
Si nota che la freccia positiva in pratica elimina il problema della divergenza torsionale delle ali.
45
Anche la distribuzione di portanza in apertura alare è fortemente condizionata dal fatto che la freccia sia in avanti (Λ < 0) o all’indietro (Λ > 0). La figura seguente [7] mostra tale fenomeno considerando il carico aerodinamico agente sull’ala di intensità costante. Tale situazione può essere ottenuta imponendo un valore opportuno, ogni volta, dell’angolo d’incidenza αr dell’ala rigida per ottenere lo stesso valore di portanza (L) agente sull’ala:
Fig. 4.9 Distribuzione di portanza al variare dell’angolo di freccia tenendo costante la portanza totale agente sulla semiala.
Da un punto di vista meramente strutturale il momento flettente alla radice dell’ala è molto maggiore per un’ala con freccia in avanti piuttosto che per un’ala con freccia all’indietro a parità di portanza (L) agente sull’ala e questo si traduce in una struttura più pesante e di conseguenza meno efficiente strutturalmente e dal punto di vista della prestazioni.
In conclusione, dal punto di vista aeroelastico la freccia all’indietro è migliore sia dell’ala diritta sia dell’ala con freccia in avanti per quanto riguarda il fenomeno della divergenza e per la distribuzione dei carichi in apertura. Quest’ultimo fenomeno, infatti, affligge fortemente il momento flettente alla radice e di conseguenza il peso della struttura.
46
4.3 Aeroelasticità dinamica
Si parla di aeroelasticità dinamica quando si considerano quei fenomeni che presentano interazione fra forze elastiche, aerodinamiche e d’inerzia. Si da, qui, principale importanza al fenomeno chiamato Flutter che descrive l’instabilità dinamica della struttura che di solito porta a conseguenze catastrofiche per quanto riguarda l’integrità della struttura.
Flutter: instabilità dinamica del velivolo associata all’interazione delle forze aerodinamiche, elastiche e inerziali della struttura. Il Flutter delle superfici portanti è quello più comunemente trattato e quello che porta a conseguenze più pericolose per il velivolo. La normativa stabilisce che per gli aerei civili le superfici portanti devono essere sempre esenti da instabilità dinamica, Flutter, in ogni punto dell’inviluppo di volo della macchina .
Si usa la rappresentazione modale per impostare l’analisi di Flutter delle superfici portanti del velivolo come un set di equazioni lineari differenziali. Si formula un problema agli auto-valori auto-vettori e le caratteristiche di stabilità sono studiate in termini di auto-valori.
Si tratta, poi, un esempio di un sistema, con aerodinamica stazionaria, con due gradi di libertà, per esporre tale metodologia. Successivamente in un altro esempio Si riporta l’analisi classica di Flutter che considera gli effetti non stazionari dell’aerodinamica.
Il Flutter delle superfici portanti può essere descritto da un set di equazioni differenziali lineari relative alla dinamica strutturale, che includono una rappresentazione lineare dei carichi aerodinamici in termini di deformazione elastica.
La natura del Flutter è tale da creare componenti di portanza e momento non stazionarie sulle superfici portanti e genera forze di natura dinamica in risposta alle perturbazioni del campo aerodinamico dovute al moto dell’ala trasversale e in beccheggio. Il moto in beccheggio deriva dalla torsione dell’ala e il moto trasversale deriva dalla flessione. Importante per l’analisi di Flutter considerare i modi rigidi che possiede la struttura. Questi ultimi danno un contributo notevole alle forze aerodinamiche le quali alimentano il fenomeno del Flutter. Quando una superficie portante si trova in un flusso al di sotto della velocità di Flutter, le oscillazioni della struttura svaniscono con un prefissato decremento esponenziale. L’aerodinamica fornisce smorzamento al moto oscillatorio della superficie portante.
Sopra la velocità di Flutter l’aria eccita il moto strutturale invece che smorzarlo e di conseguenza le oscillazioni divergono esponenzialmente fino al collasso delle superfici portanti.
47
4.3.1 Metodo p
Adesso si osserva la soluzione di un problema di dinamica strutturale in presenza di carichi aerodinamici. La struttura del velivolo è ipotizzato essere rappresentata in termini di “modi di vibrare”. La superficie portante è rappresentata come una piastra; w(x,y,t) è definito lo spostamento in direzione ortogonale alla piastra, i modi normali di vibrare sono rappresentati da φi(x,y) e l’associata frequenza naturale modale è ωi [7].
Lo spostamento trasversale della struttura in termini di rappresentazione modale è così scritto:
Con rappresentiamo la coordinata generalizzata del modo i-esimo.
Il set di equazioni generalizzate che rappresentano la dinamica strutturale del velivolo sono di seguito riportate:
La massa generalizzata è rappresentata da e le forze generalizzate da . Le uniche forze esterne che vanno nel computo delle forze generalizzate sono le forze aerodinamiche.
La distribuzione di pressione Δp(x,y,t) sull’ala può essere descritta come funzione lineare delle coordinate generalizzate e delle sue derivate come di seguito riportato:
48
Dopo vari passaggi matematici otteniamo la relazione del moto nella forma seguente:
Dato che il set di equazioni, rappresentanti il moto è omogeneo, la soluzione può essere vista come una semplice funzione esponenziale del tempo sempre in termini di coordinata generalizzata:
exp(vt) (eq.4.41) Si sostituisce l’eq. 4.41 nella 4.40 e elaboriamo un problema agli auto-valori auto-vettori. Si ricava l’equazione caratteristica e si trovano gli auto-valori che la soddisfano.
Otteniamo n+1 auto-valori complessi coniugati della forma seguente:
La soluzione dell’equazione generalizzata del moto, con l‘interazione delle forze aerodinamiche assume la seguente forma:
Dove è il complesso coniugato di .
Dalla relazione, eq. 4.43, si vede che il k-esimo componente della sommatoria rappresenta un’oscillazione armonica che decresce o cresce nel tempo secondo una funzione esponenziale.
49
La natura della risposta dinamica, una volta assegnate le condizioni al contorno, è fortemente dipendente dal segno dello “smorzamento” .
Nei grafici seguenti [7] si riporta l’andamento qualitativo della risposta dinamica del sistema in funzione del parametro considerando sempre diverso da zero. Se quest’ultimo parametro fosse uguale a zero la risposta non sarebbe oscillatoria;
Fig.4.10 Risposta dinamica al variare di con
Si chiama“smorzamento modale” del k-esimo modo di vibrare che ha il sistema il valore quando è negativo e è definita “frequenza modale” del medesimo modo.
50
Si trattano i moti dal punto di vista della stabilità. Quando le oscillazioni convergono e la risposta del sistema è dinamicamente stabile, invece, quando le oscillazioni della struttura divergono e il sistema è dinamicamente instabile. Il caso limite in cui rappresenta il “margine di stabilità”: Gli autovalori soluzione del problema sono immaginari puri e la risposta è semplicemente armonica. Si ricorda che tutte queste asserzioni sono vere nel caso in cui la frequenza modale , altrimenti la risposta non è oscillatoria.
Per un sistema aeroelastico la condizione di instabilità dinamica è il “Flutter”, con e
e il margine di stabilità corrispondente ad una risposta puramente armonica è
chiamato “margine di Flutter”, con con e .
L’eq. 4.43 [7] mostra che lo spostamento di un generico punto del sistema è data dalla somma dei vari contributi modali, per questo sembra opportuno riportare di seguito una tabella che riassume tutte le possibili condizioni del moto che la risposta dinamica del sistema sotto l’azione delle forze aerodinamiche, può presentare al variare dello “smorzamento modale” e della “frequenza modale” ;
Tab. 4.1 Tipi di moto e caratteristiche di stabilità al variare dei parametri e
Quando e si tratta il problema aeroelastico statico della divergenza. Inoltre, quando e , la risposta dinamica del sistema è indipendente dal tempo e si dice che siamo sul margine di divergenza. Il metodo sopra esposto per l’analisi dell’instabilità dinamica nota con il nome di Flutter è indicato in molti testi come “Metodo p” [7] così chiamato per la presenza dell’auto-valore complesso coniugato p=bν/U presente nell’eq. del moto, eq. 4.43.