1
A
NALISI DELLO SCATTERING DA SUPERFICI RUGOSE1.1 Scattering da superfici rugose: caratteristiche generali del problema
Quando un’onda elettromagnetica incide sull’interfaccia tra due mezzi, elettromagneticamente omogenei, si è in presenza di un fenomeno di scattering superficiale: parte dell’energia è diffusa nel primo mezzo, quella rimanente è invece trasmessa nel secondo mezzo.
Trascurando i fenomeni di trasmissione si possono distinguere due casi:
• l’interfaccia tra due mezzi è piana (o comunque la rugosità trascurabile secondo i criteri descritti in 1.2) l’onda elettromagnetica viene riflessa secondo leggi ben note [24]. In generale la componente riflessa dipenderà dalla lunghezza d’onda, dall’angolo d’incidenza e dalle proprietà elettriche dei due mezzi;
• l’interfaccia presenta un rugosità non trascurabile [1.2] che complica notevolmente il problema dello scattering.
Figura 1.1.1 Variazione qualitative del diagramma al variare della rugosità.
Qualitativamente una superficie piana rifletterà un’onda incidente in una singola direzione (quella speculare), mentre una superficie rugosa la diffonderà in varie direzioni
2
(alcune delle quali saranno privilegiate). In questo caso si dovrà tenere conto anche dei parametri statistici che descrivono la superficie [1.2].
Osservando Figura 1.1.1 [8], si ha che per superfici lisce, il diagramma d’irradiazione di un’onda riflessa è una funzione del tipo Delta di Dirac centrata nella direzione speculare.
Nel caso di superfici debolmente rugose, invece, il diagramma di irradiazione è formato da due componenti: una componente in direzione speculare, ed una componente diffusa che tiene conto della potenza dell’onda incidente reirradiata in tutte la direzioni.
Infine, nel caso di superfici molto rugose, il diagramma di reirradiazione diventa quello relativo ad una superficie Lambertiana [8].
All’aumentare della rugosità, l’onda riflessa inizia ad essere attenuata a causa della potenza che viene scatterata in tutte le direzioni dal punto d’incidenza. La potenza riflessa, solitamente, prende il nome di componente speculare (coherent power) mentre quella scatterata è detta componente diffusa (incoherent power).
punto d’incidenza
RX (Pr,Gr)
TX (Pt,Gt)
(R2,θ
s,φ
s)
(R1,θ
i,φ
i)
Figura 1.1.2 Raggio riflesso dalla superficie
La potenza scatterata di tipo incoerente ricevuta sarà:
2 3 2 1 2 ( , ) ( , ; , ) (4 ) ( ) t r r s s t s s G G P P R R λ θ φ ρ θ π = φ θ φ (1.1.1)
ricevuta si ottiene integrando sull’area illuminata s∆ . Questa dovrà essere abbastanza piccola da considerare l’onda incidente come piana ma allo stesso tempo sufficientemente grande da includere le statistiche della superficie rugosa: tipicamente s∆ dovrà essere maggiore della lunghezza di auto correlazione di z [par. 1.2].
La potenza coerente potrà invece essere ricavata dalla seguente formula: 2 2 2 3 2 1 2 (4 ) ( ) t r r t G G P P Rf R R λ χ π = + (1.1.2) dove Rf è il coefficiente di riflessione per la superficie liscia, mentre χ ≤ tiene conto delle 1
4
1.2 Caratterizzazione di una superficie rugosa
Il fenomeno della reirradiazione da una superficie dipende dalla scala di rugosità della superficie stessa in relazione alla lunghezza d’onda della radiazione incidente e dall’angolo d’incidenza.
Due parametri statistici vengono, di solito, usati per caratterizzare la rugosità della superficie: la deviazione standard dell’altezza della superficie σz e la lunghezza di correlazione della superficie L.
Se consideriamo la funzione come rappresentazione dell’andamento dell’altezza superficiale rispetto al piano
( , )
z x y
( , )x y di un sistema di riferimento cartesiano ortogonale, per una
porzione di superficie definita come piastra di dimensione Lx e Ly, l’altezza media vale:
/ 2 / 2 / 2 / 2 1 ( , ) y x x y L L x y L L z z x y dxdy L L − − =
∫ ∫
(1.2.1) ed il momento del secondo ordine:/ 2 / 2 2 2 / 2 / 2 1 ( , ) y x x y L L x y L L z z x y dxdy L L − − =
∫ ∫
(1.2.2) quindi la deviazione standard del profilo dell’altezza è:2 2
z z z
σ = − (1.2.3) Per definire la lunghezza di correlazione L è necessario definire prima la funzione d’autocorrelazione normalizzata: / 2 / 2 / 2 / 2 / 2 / 2 2 / 2 / 2 ( , ) ( , ) ( , ) ( , ) y x x y y x x y L L L L L L L L z x y z x x y y dxdy R x y z x y dxdy − − − − + + =
∫ ∫
∫ ∫
(1.2.4)Quest’ultima rappresenta una misura della similarità tra l’altezza z nel punto ( , )x y e
quella relativa ad un punto ( ', ')x y , di coordinate (x+x y, +y) rispetto a ( , )x y .
Nel caso discreto (monodimensionale per semplicità), la funzione di autocorrelazione normalizzata per una distanza di x' (= j− ∆x1) dove j è un intero maggiore di 1 è data da []:
1 1 1 2 1 ( ') N j i j i i N i i z z R x z + − + − = = =
∑
∑
(1.2.5)dove N rappresenta il numero di campioni considerati.
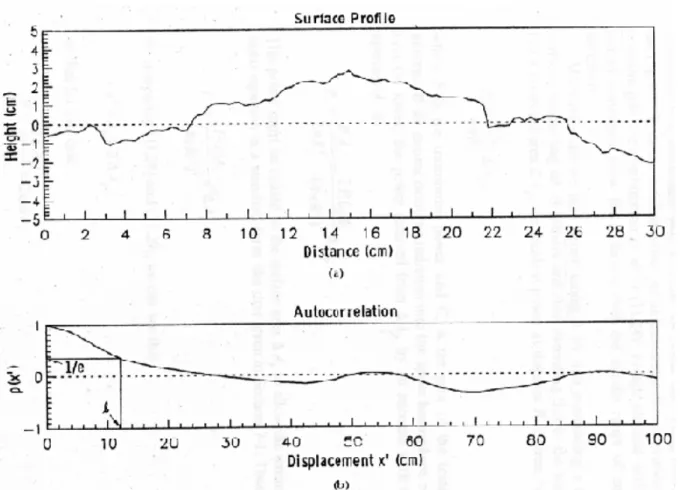
La lunghezza di correlazione superficiale L è definita come lo scostamento del punto
( ', ')x y dal punto ( , )x y tale che la funzione di autocorrelazione normalizzata R x y( , ) sia
uguale a 1/ (Figura 2.2.1); cioè se e R x y( , ) 1 e
= allora L= (x−x') (+ y− ') . y
Considerando le altezze distribuite come una gaussiana a valor medio nullo e varianza
z
σ si ha la distribuzione di probabilità espressa da: 2 1 ( ) 2 1 ( ) 2 z h z z p h e σ πσ − = (1.2.6) e la relativa funzione d’autocorrelazione:
2 2 ( ) l L l e ρ = − (1.2.7)
6
Figura 1.2.1 a) Esempio di profilo superficiale delle altezze, b) funzione di autocorrelazione corrispondente.
La lunghezza di correlazione è un parametro utile per stimare l’indipendenza statistica di due punti della superficie: se due punti sono separati da una distanza maggiore di L allora le loro altezze possono essere considerate (approssimativamente) statisticamente indipendenti una dall’altra; nel caso limite di superficie perfettamente liscia, ogni punto della stessa è correlato a qualsiasi altro punto con un coefficiente di correlazione unitario, in tal caso la lunghezza di correlazione è L→ ∞.
Nell’approccio a problematiche di scattering da superfici rugose in prima analisi è importante determinare il grado di rugosità della superficie in esame: ciò consiste nel trovare un valore di controllo che indichi se tener conto o meno del fenomeno. La rugosità inoltre non può essere classificata in assoluto ma deve essere, ogni volta, messa in relazione rispetto ai parametri che caratterizzano l’onda incidente, quali ad esempio lunghezza d’onda e angolo d’incidenza, oltre che in relazione alle caratteristiche statistiche della superficie.
Figura 1.2.2 Rappresentazione di una generica superficie rugosa
Considerando un’onda localmente piana incidente su una superficie con un angolo d’incidenza θ (Figura 1.2.2), questa può essere considerata liscia o rugosa: se la lunghezza d’onda è molto maggiore della massima differenza di altezza allora la superficie sarà considerata liscia, altrimenti se h è dell’ordine della λ si dovrà tener conto dell’effetto della rugosità.
In altri termini si può esprimere il criterio considerando il parametro ∆ϕ ( per quanto riguarda l’altezza delle ondulazioni), pari alla massima differenza di fase tra il raggio riflesso dal punto più alto della superficie e quello riflesso dal punto più basso della rugosità:
l
∆
∆ =l 2 cos( )h θ (1.2.8)
∆ =ϕ 2 cos( )kh θ (1.2.9)
dove k =2 /π λ è il numero d’onda.
Se la superficie è liscia i due raggi sono riflessi in fase (l’angolo di riflessione è lo stesso di incidenza per il teorema di Snell), mentre se è rugosa sono sfasati di ∆ϕ. Se la differenza di fase ∆ϕ è piccola la superficie viene considerata liscia e i raggi si approssimano in fase, altrimenti si tiene conto della rugosità. Il valore limite di sfasamento ∆ϕ è fissato in
/ 2
π per il criterio di Raylegh e in / 8π per il criterio di Fraunhofer [7,8]. Data la maggior restrittività, soprattutto nelle applicazioni ad alta frequenza, nelle simulazioni che verranno descritte [cap. 3] si è scelto il secondo criterio che porta alla seguente formulazione: una superficie è considerata liscia se
8 32 cos( ) h λ θ ≤ (1.2.10)
Il parametro h ci fornisce informazioni riguardo la superficie in esame ed assume un significato diverso a seconda dei casi:
• la funzione che descrive la superficie è nota (caso deterministico) allora h assume il significato di altezza media:
( , )
z x y
h= z (1.2.11)
• la superficie può essere considerata solo mediante statistiche della variabile aleatoria z x y( , ), allora h assume il significato di deviazione standard:
h=σz (1.2.12)
Nei casi pratici non si avrà mai a che fare con una superficie nota in senso deterministico.
Il problema dello scattering da superfici rugose è di difficile soluzione e non esiste una soluzione in forma chiusa valida per tutte le scale di rugosità. I metodi più comunemente utilizzati sono il metodo di Kirchhoff e il metodo delle piccole perturbazioni. Le regioni di applicabilità dei due metodi sono complementari, nel senso che il metodo di Kirchhoff è applicabile quando la scala di rugosità della superficie è maggiore della lunghezza d’onda elettromagnetica, o comparabile con essa, mentre il metodo delle piccole perturbazioni è applicabile solo nel caso di superfici debolmente rugose.
1.3 Metodo di Kirchhoff
Il metodo di Kirchhoff utilizza la tipica approssimazione dell’ottica fisica: essa consiste nel valutare la distribuzione del campo elettromagnetico tangente alla superficie S facendo riferimento a problemi canonici semplificati che ben approssimano localmente le caratteristiche geometriche del problema.
In particolare nel calcolo delle componenti tangenziali del campo elettrico e magnetico in un punto della superficie S, si ricorre ad un problema equivalente in cui S, nell’intorno del punto in esame, viene sostituita da un piano tangente ad essa. Ipotizzando che detto piano rappresenti l’interfaccia tra due mezzi con le stesse caratteristiche elettriche di quello sovrastante e di quello sottostante la superficie, è possibile utilizzare i risultati ottenuti per la riflessione da una superficie piana infinita.
In generale l’approssimazione di Kirchhoff si applica per ottenere una soluzione semplice e ragionevole nel caso di superfici caratterizzate da una scala di rugosità e da un raggio medio di curvatura che risultino grandi rispetto alla lunghezza d’onda elettromagnetica. In altri termini la lunghezza di correlazione L deve essere maggiore della lunghezza d’onda della radiazione incidente, mentre la deviazione standard delle altezze della superficie σz
deve risultare sufficientemente piccola affinché il raggio medio di curvatura della superficie sia più grande della lunghezza d’onda elettromagnetica.
L’applicabilità del criterio si può formalizzare matematicamente nelle seguenti relazioni:
kL≥6 (1.3.1) 2 2.76
z
L ≥ σ λ (1.3.2)
Si può osservare che la necessità di dover approssimare la superficie con il piano ad essa tangente si traduce in una limitazione per le dimensioni minime delle faccette che la discretizzano.
Considerando un’onda incidente su di una superficie con piano di incidenza ( , )x z e
angolo di incidenza iθ ; assumiamo che l’onda sia descritta da una funzione scalare (si pensi ad un’onda elettromagnetica polarizzata linearmente).
10
Figura 1.3.1 Punto d’incidenza sulla piastra r’e punto r in cui si va a valutare il campo.
Il campo incidente è dato da:
i( ) ik ri i(
E r =e =e β γx− z)
(1.3.3) dove: ki =ksin( )θi x kˆ− cos( )θi zˆ=βxˆ−γzˆ, , k 2π
λ
= .
ˆ ˆ ˆ
r=xx+yy+zz
Il campo E r( ) nel punto prodotto dal campo r E r( ') presente sulla superficie S nel
punto può essere espresso in maniera scalare dall’integrale di Helmoltz (basato sulla funzione di Green): ' r ∈S ( ) ( ') ( , ') ( , ') ( ') ' ' ' o o S dG r r dE r E r E r G r r dS dn dn ⎡ ⎤ = ⎢ − ⎥ ⎣ ⎦
∫
(1.3.4) dove è la normale uscente dalla superficie nel punto consideratoee n' '
0( , ') / 4 '
ik r r
G r r =e − π r− è la funzione di Green. r
Per risolvere il problema abbiamo bisogno di alcune ipotesi semplificative. La prima di queste è che il punto d’osservazione di r di coordinate ( , , )Rθ φs s sia posto nella regione di
campo lontano, in modo che:
k r−r' ≅kR k r− s '
s z
(1.3.5) dove ks =ksin( ) cos( )θs φs xˆ+ksin( )sin( )θs φs yˆ+kcos( )θ ˆ.
Si ottiene quindi: 0 0 ' ' s dG ik n G dn = − ⋅ (1.3.6)
Restano comunque come incognite E r( '), . Si usa a questo punto
l’approssimazione di Kirchhoff, che da il nome al metodo in esame, cioè si impone che la superficie sia localmente piana. Si ottiene quindi:
( ') / ' dE r dn ( ') i( ')(1 ) f E r =E r +R (1.3.7) ( ') ' ( ') ' ( ') ' i i i i dE r ik n E r ik n E r R dn = ⋅ − ⋅ f (1.3.8)
dove Rf è il coefficiente di riflessione nel punto ' e dipende dall’angolo d’incidenza, dalla
normale alla superficie, dalle proprietà elettriche del materiale e dalla polarizzazione dell’onda incidente (orizzontale o verticale). Il coefficiente
r
f
R può essere espresso come la
somma di un coefficiente Rf0 riferito ad una superficie liscia e di un coefficiente Rfrche tiene
conto della rugosità. Se la superficie varia lentamente Rfr è piccolo in confronto a Rf0 per
cui Rf =Rf0+Rfr ≅Rf0.
Sostituendo le nuove espressioni ottenute nella (1.3.4) si ha che: ' ( ) ( ' ') ' 4 ikR iv r f S e E r i v n R w n e dS R π ⋅ =
∫
⋅ − ⋅ (1.3.9) dove: v= −ki ks =v xxˆ+v yyˆ+v zzˆ w= +ki ks =w xxˆ+w yyˆ+w zzˆvx = −k(sin( ) cos( ) sin( ))θs φs − θi
vy = −ksin( )sin( )θs φs
vz = −k(cos( ) cos( ))θs + θi
wx = −k(sin( ) cos( ) sin( ))θs φs − θi
wy = −ksin( )sin( )θs φs wz = −k(cos( ) cos( ))θs + θi r'=x x'ˆ+y y'ˆ+z x y z( ', ')ˆ z n'=n xxˆ+n yyˆ+nzˆ ' ' ' z dx dy dS n = v n dS' ' vxdz x y( , ) vydz x y( , ) vz dx dy' dx dy ⎛ ⎞ ⋅ = −⎜ − + ⎟ ⎝ ⎠ '
12 w n dS' ' wxdz x y( , ) wy dz x y( , ) wz dx dy' ' dx dy ⎛ ⎞ ⋅ = −⎜ − + ⎟ ⎝ ⎠
Sostituendo i termini fin qui ottenuti nella (1.3.9) compaiono integrali nella forma ' ( , ) ' iv r S dz x y e dx dy dx ⋅
∫
' e ( , ) ' ' ' che in generale non possono essere risolti. In particolare, la procedura adottata in [1] prevede un’integrazione per parti. Con opportune considerazioni sui due termini che derivano dalla (1.3.9) si trascura uno dei due e si ottiene così: iv r S dz x y e dx dy dy ⋅∫
( ) ' ' ' 4 ikR iv r S e E r i F e dx dy R π ⋅ =∫
(1.3.10) dove:2 (1 cos( ) cos( ) sin( ) cos( )sin( )) 0
cos( ) cos( ) s i s s i f i s k F θ θ θ φ θ R θ θ + − = − +
L’espressione generale (1.3.10) diviene quindi:
' 0 0 1 ( ) ( , , ) ( , ,0) ( , , ) iv r ' ' s s i i s s S E r E R E R f e dx dy S θ φ θ θ θ φ ⋅ = =
∫
(1.3.11) dove:1 cos( ) cos( ) sin( ) cos( )sin( )
(cos( ) cos( )) cos( )
i s s s i s i f θ θ θ φ i θ θ θ + − = + θ .
Questa è l’espressione generale del campo nell’approssimazione di Kirchhoff. Osserviamo che se la superficie fosse piatta allora v r⋅ =' v xx +v yy e il campo che si ottiene nella direzione
speculare θ θi = ,s φs = è dato da: 0
0( ) 0( , , 0) ( 2 cos( )) 0 ' ' 4 ikR i i S e f E r E R i k R dx dy R θ θ π = = −
∫
(1.3.12)1.3.1 Componente di campo riflessa
Considerando per prima cosa la sola componente di campo riflessa. Dalla (1.3.11) considerando che f =1 per θ θi = s φs = , si ha: 0
( , ) 0 ( , , 0) ( , , 0) iv z x yz i i E r θ =E Rθ e (1.3.1.1) ma iv z x yz ( , )
e non è altro che la funzione caratteristica della variabile aleatoria z x y( , ), cioè
( , ) ( ) ( ) z z iv z x y iv z z e p z e dz χ z +∞ −∞ =
∫
= sdove con p z( )si è indicata la funzione di probabilità di z. Ricordando che per θ θi = si ha vz = −2 cos( )k θi , si ottiene che il fattore usato
nell’espressione ( , )
( 2 cos( ))
z
iv z x y
i
e =χ − k θ che non è altro che il fattore usato
nell’espressione della potenza (1.1.2). La componente coerente in una generica direzione risulta invece: ( , , ) ( , ,0) ( , , )1 i v x( x ' v yy ') ( ) s s i i s s S z E R E R f e S θ φ ⎡ θ θ θ φ + ⎤χ = ⎢ ⎥ ⎣
∫
⎦ v (1.3.1.2)1.3.2 Componente di campo diffusa (coefficienti di scattering)
Per calcolare i coefficienti di scattering viene usata la seguente espressione: 2 2 , , 2 1 4 ( , ) S p q p q R E i i S π ρ ρ= = ∆ (1.3.2.1)
che, sottraendo al campo la componente coerente risulta: 2 2 , 2 1 4 ( , ) p q R E E i i S π ρ ρ= = − ∆ (1.3.2.2) Si ottiene cosi: 2 2 2 0 cos ( )i f k R f I θ ρ π = (1.3.2.3) dove 1 ' ' '' '' ivx( 'x x'') ivy( 'y y'') 2( , ) ( )2 z z z S S I dx dy dx dy e v v v S χ χ − + − ⎡ ⎤ = − − , e la χ è la
funzione caratteristica congiunta della variabile aleatoria z=ζ( , )x y :
⎣ ⎦
∫
∫
2( , )v v1 2∫ ∫
+∞ ∞ − +∞ ∞ − + + = = 1 2 1 2 2 1 2( , ) 11 2 2 (ς ,ς ) 11 2 2 ς ς χ v v eivς ivς pz eivς ivς d d (1.3.2.4)Considerando ora la variabile aleatoria z=ς( yx, )normalmente distribuita con
14 20 2 2 0 2 1 ) ( ) ( σ ς σ π ς = − = p e z pz z (1.3.2.5) 2 2 2 0 z z v iv e e σ ς = − (1.3.2.6) (1 ) 2 2 / 1 2 2 0 2 1 2 2 0 2 2 2 1 2 1 ) 1 ( 2 1 ) , ( C C z e C p − + − − − = σ ς ς ς ς πσ ς ς (1.3.2.7) dove C=C(δ)e’ dato da:
ς(x1,y1)ς(x2,y2) =σ02C(δ) δ= xd2+ yd2 xd = x1−x2 yd = y1−y2 Segue pertanto: χ2( , ) v2σ02[1 C(δ)] z z v e z v − = − − (1.3.2.8) ⎥⎦ ⎤ ⎢⎣ ⎡ − = − − ) ( ) − 1 , ( 2 ( ) 2 2 0 2 2 0 2σ σ δ χ χ v v C z z z v v e z e z v (1.3.2.9)
Se la superficie è leggermente rugosa, si può usare la seguente approssimazione:
, (1.3.2.10) alla fine si riesce ad esprimere I come:
) ( 1 2 20 ) ( 2 0 2 δ σ δ σ C v evz C − ≅ z I = π2W(−vx,−vy) (1.3.2.11)
dove W(p,q) e’ di nuovo la densità spettrale dell’altezza superficiale definita rispetto ai parametri superficiali. Segue pertanto: ) , ( ] sin cos sin cos cos 1 [ ) , , (θi θs φs =πk4Rf0 + θs θi − θs φs θi 2W −vx −vy ρ (1.3.2.12)
Per il backscattering si ha:
( , , ) b 4 4 f0 ( 2 sin i,0)
i
i θ π ρ πk R W k θ
θ
16
y
1.4 Metodo Perturbativo del Primo Ordine
Considerando una superficie descritta dalla seguente funzione z=ζ( , )x e scegliendo
di rappresentare la deviazione standard della rugosità dal valore medio pari a zero. La tecnica è applicabile quando la differenza di fase dovuta alla è molto inferiore a h 2π e la pendenza
del profilo sia minore dell’unità. Questa condizione si traduce matematicamente nelle seguenti espressioni: kσzcoa( )θi 1 d 1 dx ζ (1.4.1) d 1 dy ζ
Considerando una porzione di piano 2
S L
∆ = (superficie perfettamente conduttrice) e un’onda incidente polarizzata orizzontalmente (il caso di polarizzazione verticale sarà trattato in maniera analoga).
Su una superficie rugosa il campo totale è dato dalla somma di tre contributi: componente incidente, riflessa e scatterata:
(1.4.2) rispettivamente esprimibili dalle seguenti formule (per quanto riguarda la direzione di campo lungo ): ( , ) i( , ) r( , ) s( , ) y y y y E x z =E x z +E x z +E x z y i( , ) i( ) y E x z =e β γx− z (1.4.3) r( , ) i( ) y E x z = −e β γx+ z
dove sin( )β =k θi e γ =kcos( )θi .
Il fatto di aver considerato una porzione di superficie 2
S L
∆ = ci permette di esprimere tutti i campi scatterati in termini di trasformata di Fourier bidimensionale nella direzione x e y con periodo L. Matematicamente:
( , ) , ( , ; ) s y m n m n E x z =
∑∑
B E v+m n z (1.4.4) dove 2 2 ( ) ( , ) ( , ; ) iL v m x i Lny i v m n z E v m n z e e e π π β + ++ = e v è un intero tale che 2 v ksin( )i
L
π = θ =β
. Questa implica che, assegnata λ, bisogna variare il valore di in modo che v θi possa essere
Poiché E x zy( , ) deve soddisfare l’equazione d’onda, β(v+m n), deve soddisfare la: 2 ( ) 2 2( , ) v m n b v m n k L L π π ⎡ + ⎤ ⎡+ ⎤+ + = 2 ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ (1.4.5)
Quella fornita sopra è la rappresentazione armonica spaziale del campo. Si noti che la (1.4.4) contiene il termine che rappresenta l’onda propagatesi nel verso positivo dell’asse z, ma non il termine che rappresenta il termine che si propaga verso z decrescenti. La soluzione, così com’è, sarebbe incompleta perché non tiene conto dell’onda che si propaga nel verso negativo tra il valore massimo e quello minimo del profilo. Quest'approssimazione è accettabile se la pendenza della rugosità della superficie non è maggiore di 0.4: questa ipotesi prende il nome di ipotesi di Raylegh.
( , ) i v m n z eβ + ( , ) i v m n z e−β +
Le altre componenti di campo (lungo x e z) sono esprimibili dalle seguenti espressioni: ( , ) s( , ) , ( , ; ) x x m n m n E x z =E x z =
∑∑
A E v+m n z (1.4.6) ( , ) ( , ) , ( , ; ) s z z m n m n E x z =E x z =∑∑
C E v+m n z (1.4.7)I coefficienti Am n, , Bm n, e non sono tra loro indipendenti essendo legati
dall’equazione , per cui si avrà: , m n C 0 E ∇i = 2 , , , 2 2 (v m A) m n nBm n b v( m n C, ) m n 0 L L π + + π + + = 0 (1.4.8) Imponiamo ora le condizioni al contorno. Sia il versore normale uscente dalla superficie, si avrà:
n
(1.4.9) che tradotto in componenti x, y risulta:
tang ( )
E = −E n E ni =
Ex−n E nx( i ) 0=
(1.4.10) Ey−n E ny( i )=0
Le componenti del versore n sono relazionabili alla superficie z=ζ( , )x y nel seguente
modo x z n d dx n ζ = − e y z n d dy n ζ
18 2 2 ˆ 1 d d x z dx dx n d d dx dy ζ ζ ζ ζ − − + = ⎛ ⎞ ⎛ ⎞ +⎜ ⎟ +⎜ ⎟ ⎝ ⎠ ⎝ ⎠ (1.4.11)
Al momento si ha un’espressione generale del campo in funzione dei coefficienti Am n, , ,
m n
B e Cm n, sconosciuti e due condizioni al contorno.
In generale è impossibile applicare queste condizioni al contorno per ottenere una soluzione analitica perché le equazioni sono accoppiate. La soluzione è ricavabile se si opera uno sviluppo in serie di Taylor dei valori dei coefficienti del campo e delle componenti del versore normale alla superficie. Tale sviluppo è possibile se imponiamo che la variazione del profilo sia una quantità piccola, così come la pendenza della superficie stessa. Indicando con
ε tale quantità si ha:
z d d k dx dy ζ ζ ε ≈ σ ≈ ≈
(1.4.12) da cui seguono i limiti di validità del metodo già discussi inizialmente. Si può allora operare la seguente espansione:
( )3 x d n o dx ζ ε = − + ( )3 y d n o dy ζ ε = − + (1.4.13) 1 ( 3 z n = +o ε )
Sostituendo nella (1.4.10) si ottiene:
x z 0 d E E dx ζ = = (1.4.14) Ey d Ez 0 dy ζ = =
La stessa espansione è fatta sui coefficienti Am n, , Bm n, e Cm n, :
(1.4.15) e sulla funzione: (1) (2) , , , ... m n m n m n A =A +A +
( , ; ) ( , ;0) 1 ( )2
E v+m n z =E v+m n ⎣⎡ +ibζ +o ε ⎤⎦
(1.4.16)
Usando queste espansioni si può scrivere l’espressione del campo scomposto nelle sue tre componenti x, y, z: (1) (2) , , ... ( , ;0)(1 ...) x m n m n m m E =
∑∑
⎡⎣A +A + ⎤⎦E v+m n +ibζ + (1.4.17) (1.4.18) (1) (2) , , 2 ( ...) i x ... ( , ;0)(1 ...) y m n m n m m E = i γζ + eβ∑∑
⎡⎣B +B + ⎤⎦E v+m n +ibζ + (1) (2) , , ... ( , ;0)(1 ...) y m n m n m m E =∑∑
⎡⎣C +C + ⎤⎦E v+m n +ibζ + (1.4.19)Tenuto conto di aver descritto il profilo dell’altezza con una trasformata di Fourier bidimensionale: 2 2 ( ( , ) ( , ) m n i x i y L L m n x y P m n e π π ζ =
∑∑
+ ) (1.4.21) e eguagliando i termini del primo ordine [1] troviamo i coefficienti (1),
m n
A (se
volessimo i coefficienti d’ordine superiore basta eguagliare le componenti d’ordine maggiore): (1) , m n B Cm n(1), (1) , 0 m n A = ∀m n, (1) (1.4.20) , 2 ( , m n B = − i P mγ n) (1) , 2 2 ( , ) m n i L C P b m n π γ =
In conclusione, la soluzione del primo ordine ci permette di descrivere la distribuzione di campo elettrico (e quindi anche di quello magnetico semplicemente applicando l’equazione di Maxwell) come somma dei contributi di campo incidente, riflesso e scatterato. La medesima procedura va applicata al caso di un’onda incidente polarizzata verticalmente.
Fino è stata considerata la soluzione perturbativa sulla superficie considerata; andiamo ora a considerare la soluzione nella condizione di campo lontano ( 2/
r L λ ) nel punto di
20
1.4.1 Componente coerente
Consideriamo la soluzione relativa al contributo coerente. Per farlo consideriamo la (1.1.2) dove il parametro χ rappresenta l’effetto della rugosità. Nell’approssimazione del primo ordine (cioè arrestando lo sviluppo in serie di Taylor dei coefficienti al primo ordine), questo è dato semplicemente dal contributo di campo riflesso dalla superficie, cioè il parametro χ ,in modulo, risulta unitario. Questo è un’approssimazione del tutto ragionevole visto che si è ipotizzato di applicare il metodo perturbativo a superfici poco rugose.
1.4.2 Componente incoerente
Per calcolare i coefficienti di scattering, bisogna innanzitutto calcolare il campo in zona lontana: in generale il campo in un punto può essere espresso in funzione del campo presente sulla superficie data attraverso (formulazione di Franz):
r
[
]
0[
]
0 0 ( ) ( ') ( , ') ' ( ') ( , ') ' S S i E r n E r G r r dS n H r G r r dS ωε ∆ ∆ = ∇×∫
× + ∇×∇×∫
× (1.4.2.1)[
]
0[
]
0 0 ( ) ( ') ( , ') ' ( ') ( , ') ' S S i H r n H r G r r dS n E r G r r dS ωµ ∆ ∆ = ∇×∫
× + ∇×∇×∫
× (1.4.2.2) dove ' 0( , ') / 4 ' ik r r G r r =e − π r− . rIl campo lontano nel punto di coordinate ( , , )Rθ φs s è legato alla distribuzione dei campi
,
x
E Ey, Hx e Hy sulla superficie secondo le seguenti relazioni:
4 ikR ik E e I R θ = π θ 4 ikR ik E e I R φ = π φ (1.4.2.3) con: ˆ ' ( cos( ) sin( )) ( sin( ) cos( )) cos( ) iki rs
x s y s x s y s s S Iθ E φ E φ η H φ H φ θ e− ⋅ ∆ ⎡ ⎤ =
∫
⎣− + + − ⎦ dS (1.4.2.4) ˆ ' ( sin( ) cos( )) ( cos( ) sin( )) iki rsx s y s x s y s S Iφ E φ E φ η H φ H φ e− ⋅ ∆ ⎡ ⎤ =
∫
⎣ − + + ⎦ dS (1.4.2.5)dove: η= µ ε0/ 0 (costante di propagazione del mezzo) e
ˆ ˆ ˆ
sin( ) cos( ) sin( )sin( ) cos( )
s s s s s
i = θ φ x+ θ φ y+ θs z (versore nella direzione di scattering). Si
possono allora dare le espressioni dei coefficienti di scattering per le diverse polarizzazioni possibili. Supponiamo che l’onda incidente abbia modulo unitario e sia polarizzata orizzontalmente; se il ricevitore riceve in polarizzazione orizzontale si ha:
2 2 2 * , 2 2 2 4 4 h h i E R k I I L E L φ φ φ π ρ π = = (1.4.2.6) se invece il ricevitore riceve in polarizzazione verticale si ha:
2 * , 4 2 v h k I I L θ θ ρ π = (1.4.2.7) Se l’onda incidente è polarizzata verticalmente si avrà rispettivamente nei casi di ricezione orizzontale e verticale:
2 * , 2 4 h v k I I L φ φ ρ π = 2 * , 4 2 v v k I I L θ θ ρ π = (1.4.2.8) Notare che Iθ, Iφ sono diversi da quelli precedenti essendo stati ottenuti sostituendo in (1.4.2.4) e (1.4.2.5) i valori di E E H eHx, y, x y per polarizzazione verticale.
Per una superficie ruvida, (1.4.2.4) e (1.4.2.5), sono variabili aleatorie, perciò si deve scrivere più propriamente:
2 * , 4 2 h h k I I L φ φ ρ π = 2 * , 4 2 v h k I I L θ θ ρ π = (1.4.2.9) e così anche per ρ e h v, ρ . v v,
Il calcolo delle medie passa attraverso la descrizione statistica della superficie: 2 2 ( ( , ) ( , ) m n i x i y L L m n x y P m n e π π ζ =
∑∑
+ ) (1.4.2.10) dove, visto che ζ( , )x y è una variabile aleatoria, allora anche i coefficienti sarannovariabili aleatorie per le quali si ha che:
( , ) P m n P m n( , ) = (1.4.2.11) 0 * 2 0 ' ( , ) ( , ) 2 1 2 2 , ' 4 per m m n n P m n P m n m n W per m m L L L π π π ≠ ≠ ⎧ ⎪ = ⎨⎛ ⎞ ⎛ ⎞ ; ' ;n n' = = ⎜ ⎟ ⎜ ⎟ ⎪⎝ ⎠ ⎝ ⎠ ⎩ (1.4.2.12)
La funzione W p q( , ) con p=2πm L/ e q=2πn L/ è la densità spettrale dell’altezza
superficiale e rappresenta la trasformata di Fourier della funzione di correlazione dell’altezza superficiale.
Il calcolo delle medie presenti in (1.4.2.9) si svolge sostituendo s
E ed H sviluppate in s
22
Iφ. Dopo varie elaborazioni matematiche e passando allo spettro continuo (il che significa far tendere L all’infinito sostituendo così le sommatorie con integrali) si ottiene:
2 2 , ( , , ) , ( , ) ( , ) 4 h h i s s h h k fφ p q W p q π ρ θ θ φ =ρ = (1.4.2.13) dove sin( ) cos( )p=k θs φs −ksin( )θi e q=ksin( )sin( )θs φs . Allo stesso modo si avrà:
2 2 , ( , , ) , ( , ) ( , ) 4 v h i s s v h k fθ p q W p q π ρ θ θ φ =ρ = (1.4.2.14) 2 2 , ( , , ) , ( , ) ( , ) 4 h v i s s h v k fφ p q W p q π ρ θ θ φ =ρ = (1.4.2.15) 2 2 , ( , , ) , ( , ) ( , ) 4 v v i s s v v k fθ p q W p q π ρ θ θ φ =ρ = (1.4.2.16) Si ricordi che fφ, fθ sono in realtà quattro funzioni diverse: fθv, fθh, fφh e fφv.
Esplicitando queste funzioni si ottengono i quattro valori dei coefficienti di scattering: 4 2 2 2
, 4 cos ( ) cos ( ) cos ( ) ( , )
h h k i s s W ρ = π θ θ φ p q ) p q ) p q p q 4 2 2 , 4 cos ( )sin ( ) ( , v h k i s W ρ = π θ φ 4 2 2 , 4 cos ( )sin ( ) ( , h v k s s W ρ = π θ φ 4
, 4 (sin( )sin( ) cos( )) ( , )
v v k i s s W
ρ = π θ θ − φ
Per i coefficienti di backscattering (θs =θ φi; s = ) si ottiene: π 4 4 , 4 cos ( ) ( 2 sin( ),0) b h h k i W k i ρ = π θ − θ 4 2 , 4 (1 sin ( )) ( 2 sin( ),0) b v v k i W k i ρ = π + θ − θ b, 0 h v ρ = b, 0 v h ρ =
In conclusione, nella soluzione del primo ordine, la componente coerente (componente riflessa) è praticamente identica, in buona approssimazione, a quella di una superficie liscia, mentre la componente incoerente è data in termini di scattering cross section.
Il coefficiente b, h h
ρ appena trovato, è molto simile a quello che si è trovato con il metodo delle Kirchhoff; la differenza sostanziale sta nel fattore cos4θi: esso deriva dalla
dipendenza della componente magnetica da cos e da un ulteriore θi proveniente dal diagramma di irradiazione della superficie rugosa ( in totale c’e’ una dipendenza del campo totale reirradiato di un fattore , e considerando le potenze). Il metodo di
Kirchoff è da considerarsi quindi meno corretto del metodo delle piccole perturbazioni in
quanto non tiene conto correttamente degli effetti della polarizzazione poiché non utilizza in pratica le corrette condizioni al contorno.
i θ cos i θ 2 cos cos4θi