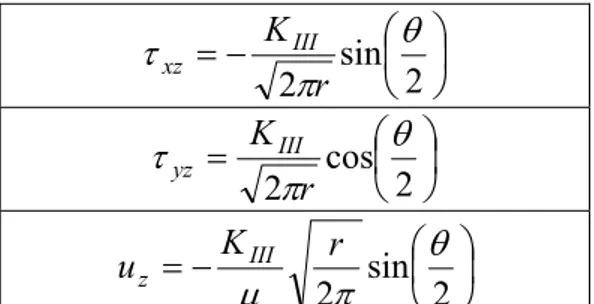CAPITOLO 3 Modelli di Meccanica della Frattura per la Verifica di Stabilità delle Fessure e loro Implementazione agli Elementi Finiti

CAPITOLO 3

Modelli di Meccanica della Frattura per la Verifica di Stabilità

delle Fessure e loro Implementazione agli Elementi Finiti

3.1 Generalità.

Ogni componente strutturale, nel momento in cui è posto in esercizio, possiede dei difetti considerati accettabili che durante il periodo di funzionamento possono accrescersi a causa di meccanismi di degradazione legati alle condizioni di carico o alle proprietà chimico-fisiche dell’ambiente di lavoro (fatica, tearing, tensocorrosione, ecc). Nel momento in cui il difetto raggiunge la dimensione critica, viene compromessa la capacità di sostenere i carichi e si ha la rottura catastrofica dell’elemento strutturale. Carichi affaticanti ed ambienti aggressivi portano ad una crescita delle fessure presenti in un componente. Più grande è il difetto e più grande è la concentrazione delle tensioni all’apice di essa, pertanto la velocità di crescita di una cricca risulta una funzione crescente nel tempo e nei cicli di carico (Figura 3.1(a)).

La resistenza di una struttura diminuisce con l’aumentare delle dimensioni di un difetto e può raggiungere un valore tale da non essere più in grado di sopportare i carichi massimi gravanti su di essa arrivando ad una rottura catastrofica. Tale possibilità diviene certezza se la resistenza assume un valore inferiore a quella necessaria per sopportare i carichi di esercizio (Figura 3.1(b)).

La Meccanica della Frattura deve fornire dei metodi e criteri per poter dare risposte quantitative a specifici problemi concernenti la presenza di fessure in componenti strutturali e determinare le seguenti quantità:

• la resistenza residua della struttura in funzione delle dimensioni della cricca;

• le dimensioni critiche di una fessura (quelle corrispondenti ad una resistenza residua inferiore a quella necessaria per sopportare i carichi di esercizio);

• il tempo necessario per far crescere una data fessura dalle sue dimensioni originali a quelle critiche;

• le dimensioni ammissibili delle cricche ad inizio vita;

• il tempo che deve intercorrere tra una ispezione e l’altra della struttura.

3.2 Concetti base di meccanica della frattura lineare elastica.

3.2.1 Il criterio energetico.

Nel caso in cui si trascurino i fenomeni dissipativi, il principio di conservazione dell’energia stabilisce che il lavoro F fatto dai carichi esterni che agiscono su un corpo debba essere trasformato in energia di deformazione U :

(3.1) F−U =0

Il lavoro F compiuto dai carichi esterni vale:

(3.2)

F

= Pds

∫

essendo P l’intensità del carico ed s lo spostamento del suo punto di applicazione. Nel piano P-s, tale lavoro è fornito dall’area sottesa dalla curva carico-deformazione. L’energia di deformazione U si calcola effettuando l’integrazione sul volume della densità di energia. Questa ultima grandezza è nota una volta conosciuto il tensore delle tensioni σ e quello delle deformazioni ε:

(3.3) Densità di energia di deformazione =

∫

σ

⋅

d

ε

Se il corpo presenta una fessura, possono verificarsi due condizioni:

• la fessura non avanza; • la fessura avanza.

Nel primo caso vale ancora l’equazione (2.1). Nel secondo caso, invece, è necessario correggere l’equazione di bilancio (2.1) introducendo un termine che tenga conto della quantità di energia spesa nella frattura del materiale. Si supponga che la fessura avanzi di una quantità infinitesima da. Se si scrive il bilancio di energia facendo riferimento alle variazioni di energia che si hanno nell’avanzamento della cricca dalla dimensione a a quella a+da , si ottiene la seguente equazione di bilancio:

(3.4)

(

F

−

U

−

W

)

=

0

da

d

che può essere riscritta nella forma:

(3.5)

da

dW

U

F

da

d

_{− )}

₌

(

Il primo membro dell’equazione (3.5) misura, l’energia rilasciata dal sistema quando la fessura avanza della quantità da; il termine a secondo membro, invece, indica la quantità di energia W necessaria per fratturare il materiale della quantità da. Questo criterio energetico stabilito da Griffith nel 1921 afferma che ‘la progazione di una qualsivoglia fessura avrà luogo se l’energia rilasciata dal sistema a seguito dell’incremento di lunghezza della cricca è sufficiente a fornire tutta l’energia richiesta perché avvenga tale incremento di fessura’. Si può dimostrare che il primo termine dell’equazione (3.5) coincide con l’energia di deformazione immagazzinata nel sistema. A titolo di esempio, si considerino i due seguenti casi:

• condizioni di controllo di spostamento (displacement control), Figura (3.2 (a)); • condizioni di controllo di carico (load control), Figura (3.2 (b)).

Si assume che in entrambi i casi il materiale possieda un comportamento elastico lineare.

Nel caso di controllo di spostamento, all’avanzamento della fessura corrisponde una diminuzione del carico applicato che passa dal valore P1 al valore P2 (Figura 3.3). L’aumento della

semilunghezza della fessura della quantità da, infatti, comporta una diminuzione della rigidezza del sistema e lo stesso spostamento può essere mantenuto con un carico applicato inferiore. L’energia elastica immagazzinata nel sistema diminuirà di una quantità pari all’area OAB e sarà rappresentata dal triangolo OBD. In questo caso i carichi esterni applicati alle estremità fisse non compiono lavoro, pertanto la propagazione della cricca può avvenire solo a spese di un rilascio di energia elastica del sistema.

Figura 3.2 Cracked plate at a fixed displacement (a) and at a fixed load (b)

L’equazione (3.5), pertanto, diventa: (3.6)

da

dW

da

dU =

−

con

<

0

da

dU

Nel caso di controllo di carico, invece, l’avanzamento della fessura avviene a carico P1

costante, cui il lavoro F compiuto da tale forza vale P₁⋅(

δ

₂ −

δ

₁), dato che le estremità della piastra subiscono lo spostamento

δ

₂ −

δ

₁ (Figura 3.4), mentre l’energia di deformazione

immagazzinata dal sistema subisce un incremento pari a













₋

2 1 1 1

2

1

2

1

_δ

_δ

P

P

. L’equazione (3.5)

assume pertanto la seguente forma:

(3.7)

da

dW

P

P

P



=











₋

−

−

⋅

_{2 1 1 1 1 2} 1

2

1

2

1

)

(

δ

δ

δ

δ

oppure, (3.8)

da

dW

P

(

− )

=

2

1

1 2 1

δ

δ

Ancora una volta, il primo membro della (3.8) rappresenta la variazione dell’energia di deformazione dU da (in questo caso essa risulta positiva in quanto i carichi esterni compiono lavoro durante la propagazione della cricca e quindi l’energia elastica del sistema aumenta anziché diminuire), mentre il secondo membro dell’equazione (3.8) coincide con l’energia richiesta per avere la frattura del materiale di una quantità da, pari all’area OAE.

Si può quindi concludere che indipendentemente dalle condizioni di carico, l’equazione di bilancio (3.5) rappresenta il criterio di rottura. Il primo membro è chiamato rateo di rilascio di energia di deformazione (strain energy release rate) all’apice della fessura o forza motrice della fessura (dato che ha le dimensioni di una forza per unità di incremento della fessura) e viene indicato con G. Il secondo membro, invece, esprime l’energia necessaria alla propagazione della cricca, per questo è chiamato resistenza alla fessurazione (fracture resistance) ed indicato con R. Il criterio di rottura espresso dall’equazione (3.5), può essere, allora, riscritto in forma sintetica:

Nel caso in cui il materiale abbia comportamento elastico lineare, si può dimostrare che G è espresso dalla relazione seguente:

(3.10)

'

2 2

E

a

F

G

₌

c

πσ

in cui:

per stato piano di tensione

per stato piano di deformazione

E

: modulo di Young del materiale;

ν

: coefficiente di Poisson del materiale;

c

F

: è un fattore che dipende dalla geometria considerata e dalle condizioni di carico;

σ

: è la sollecitazione applicata al corpo in direzione normale alla superficie di frattura;

a: semilunghezza della frattura.

Sostituendo la (3.10) nella (3.9), tenendo conto che

σ

E'=

ε

(legge di Hook), si ottiene:

(3.11)

F

_c2

πσε

a

=

R

L’equazione (3.11), stabilisce il criterio di rottura del materiale. Tale criterio, tuttavia, fornisce risultati corretti solamente se il materiale mantiene un comportamento elastico lineare (come nel caso di materiali fragili o ad alta resistenza) nella zona circostante la fessura. Se il fenomeno di frattura, invece, è accompagnato da notevoli deformazioni plastiche (come avviene per materiali molto duttili), non è più possibile effettuare un’analisi di tipo elastico e bisogna far ricorso agli strumenti messi a disposizione dalla meccanica della frattura elasto-plastica (EPFM).

Una rappresentazione grafica del criterio energetico di rottura, si ha ponendo in ordinata le grandezze G e R e suddividendo l’asse delle ascisse in due parti, a sinistra dell’origine si pone la lunghezza delle cricche e a destra si pongono gli incrementi di lunghezza delle cricche (Figura 3.5). Fissando un valore a1 della cricca ed una tensione σ2, il valore di G è rappresentato dal punto F. Per

la cricca a1, al variare della tensione fra 0 e σ2, G varia da O a F. Aumentando la tensione a σ1, G

raggiunge il punto H in cui uguaglia la resistenza a fessurazione, R. La propagazione della fessura sotto tensione σ1 avviene lungo la linea HK in corrispondenza della quale G risulta sempre

maggiore di R. Una fessura a2>a1, sollecitata da una tensione variabile da 0 a σ2, ha valori di G che















−

=

2

1

'

ν

E

E

E

variano da 0 a H (le linee LF e MH corrispondenti allo stesso valore di tensione sono parallele); ad H si ha l’inizio di propagazione della fessura che proseguirà lungo la linea HN.

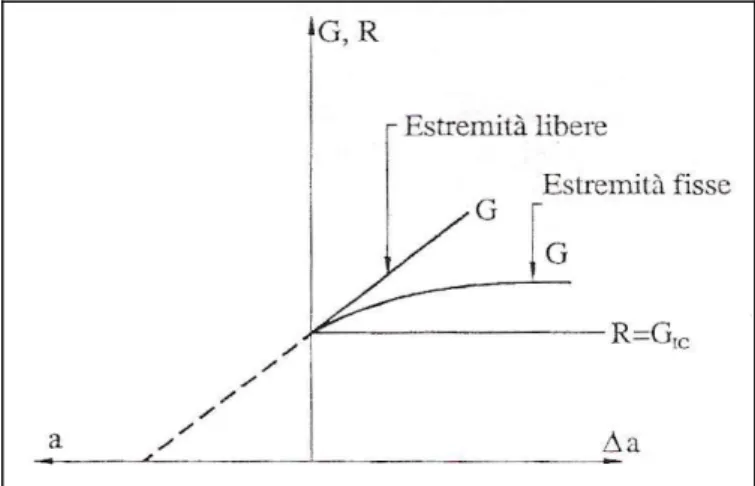
Figura 3.5 Graphical representation of instability energy criterion

Il tasso di rilascio di energia G assume lo stesso valore sia nel caso di loading control (estremità libere) sia nel caso di displacement control (estremità fisse), ma solo all’inizio della propagazione della fessura. Nella fase di ulteriore accrescimento della cricca, l’andamento di G è lineare solo nel caso di carico costante mentre nel caso di spostamento controllato G può diminuire all’aumentare di a, in seguito alla diminuzione della tensione (G aumenta in funzione di a con legge lineare) (Figura 3.6).

Figura 3.6 Difference in G for fixed grip and costant load conditions beyond instability

La resistenza alla fessurazione R nel caso di plane strain risulta indipendente dalla lunghezza della cricca assumendo così il valore costante di GIC , mentre sperimentalmente è stato

dimostrato che nel caso di plane stress essa varia con legge monotona crescente all’aumentare dell’incremento del difetto (Figura 3.7).

Ponendoci in condizioni di plane stress, considerando una cricca a1 e una tensione σ1,

l’energia G è rappresentata dal punto B. Con tensione costante all’avanzamento della fessura l’energia di deformazione varia lungo la retta BH, ma essendo i valori di G sempre inferiori a R, non si potrà avere propagazione della cricca. La tensione deve aumentare fino a σc, per cui la cricca

propagazione instabile della fessura (la retta DF risulta sempre maggiore di R. In D sono verificate le seguenti relazioni che esprimono il criterio energetico della rottura in condizioni di stato piano di tensione:

∂

G

_C

∂

a

=

∂

R

∂

a

e

G

_C

=

R

dove GC è l’energia critica a frattura.

Figura 3.7 Trend of R-curve for plane strain and plain stress

Questo criterio energetico è un ottimo strumento per la valutazione del comportamento alla fessurazione di un dato materiale e di semplice applicazione. Chiaramente la sua messa in pratica richiede la conoscenza di una opportuna espressione analitica di R o una sua valutazione per via sperimentale. Questo metodo di semplice implementazione grafica consente una valutazione del comportamento post-instabilità di una fessura e del suo possibile arresto.

3.2.2 Stato di Tensione all’apice di una fessura.

Per varie configurazioni di difetti soggetti a carichi esterni è possibile ricavare espressioni semplici e compatte per descrivere lo stato di sollecitazione nel componente, assumendo un comportamento del materiale lineare elastico. Definendo un sistema di riferimento polare centrato nell’apice della fessura (Figura 3.8), si può dimostrare che lo stato di tensione è descritto dalla seguente espressione: (3.12)

σ

( )

θ

_ij( )m

( )

θ

m m m ij ij

f

A

r

g

r

K

_∑

∞ =

+













=

0 2

in cui,

σ

_ij è il tensore degli stress, r e θ sono definiti in Figura 3.8, K è una costante e

f

_ij è una funzione adimensionalizzata. I termini di ordine più elevato dipendono dalla geometria, ma la soluzione per una qualsiasi configurazione di difetto è pilotata dal termine proporzionale a

1

r

. Per r →0, in prossimità dell’apice, il primo termine tenderà all’infinito mentre gli altri termini saranno trascurabili. L’equazione (3.12) presenta quindi una singolarità in r =0.

Figura 3.8 Definition of the coordinate axis ahead of a crack tip

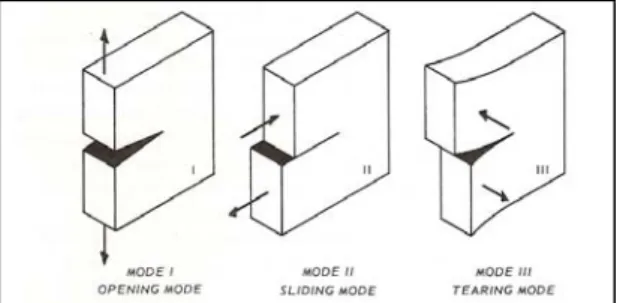
Una fessura contenuta in un materiale può essere sollecitata secondo tre differenti tipi di carico, come illustrato in Figura 3.9:

• Opening mode (Modo I), sono le tensioni normali al piano della fessura ad originare gli spostamenti dei lembi;

• Sliding mode (Modo II), sono le tensioni tangenziali nel piano della fessura stessa ad originare lo spostamento dei lembi in direzione ortogonale al bordo di attacco; • Tearing mode (Modo III), sono le tensioni tangenziali fuori dal piano della fessura

ad originare lo spostamento dei lembi in direzione parallela al bordo di attacco. La sovrapposizione dei tre modi descrive un qualsiasi problema di fessurazione.

Figura 3.9 The three modes pf loading that cam be applied to a crack

Espressioni dettagliate della singolarità dello stato di sollecitazione per i tre Modi di rottura sono riportati in Tabella 3.1 e Tabella 3.2, mentre le relazioni sugli spostamenti per i primi due modi sono riportati in Tabella 3.3.

Mode I Mode II xx

σ

_



































−













2

3

sin

2

sin

1

2

cos

2

θ

θ

θ

π

r

K

_I





































+













−

2

3

cos

2

cos

2

2

sin

2

θ

θ

θ

π

r

K

_II yy

σ

_



































+













2

3

sin

2

sin

1

2

cos

2

θ

θ

θ

π

r

K

_I





































2

3

cos

2

cos

2

sin

2

θ

θ

θ

π

r

K

_II xy

τ





































2

3

cos

2

sin

2

cos

2

θ

θ

θ

π

r

K

_I





































−













2

3

sin

2

sin

1

2

cos

2

θ

θ

θ

π

r

K

_II zz

σ

₍

0 (Plane Stress)

₎

yy xx

σ

σ

ν

+

(Plane Strain) 0 (Plane Stress)

(

σ

xx

σ

yy

)

ν

+

(Plane Strain) xz

τ

,

τ

_yz 0 0













−

=

2

sin

2

θ

π

τ

r

K

_III xz













=

2

cos

2

θ

π

τ

r

K

_III yz













−

=

2

sin

2

θ

π

µ

r

K

u

III z

Tabella 3.2 Non-zero stress and displacement components in Mode III

Mode I Mode II x

u

_























+

−













2

sin

2

1

2

cos

2

2

2

θ

κ

θ

π

µ

r

K

_I

























+

+













2

cos

2

1

2

sin

2

2

2

θ

κ

θ

π

µ

r

K

_II y

u

_























−

+













2

cos

2

1

2

sin

2

2

2

θ

κ

θ

π

µ

r

K

_I

























−

−













−

2

sin

2

1

2

cos

2

2

2

θ

κ

θ

π

µ

r

K

_II

µ

shear modulus

ν

κ

=3−4 plane strain

(

ν

) (

ν

)

κ

= 3− 1− plane stress

Tabella 3.3 Crack tip displacement fields for Mode I and Mode II

Considerando la sola singolarità generata dal Modo I di rottura sul piano contenente la fessura (θ = 0), le componenti di tensione lungo le direzioni x e y sono identiche come risulta dalla Tabella 3.1: (3.13)

r

K

_I yy xx

π

σ

σ

2

=

=

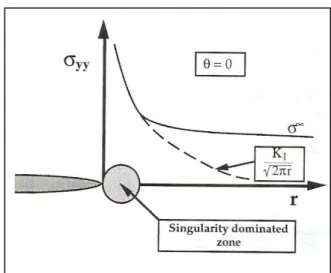
In Figura 3.10 è schematicamente rappresentata la componente normale al piano della fessura in funzione della distanza dall’apice della fessura. L’equazione (3.13) ha validità in prossimità del difetto in corrispondenza del quale la singolarità

1

r

domina il campo di tensioni. Le tensioni lontane dal difetto sono governate dalle condizioni di carico applicate in posizione remota al punto di localizzazione della fessura, per cui la tensione tenderà ad un valore finito

σ

∞(per r→∞

occorre considerare tutti i termini della serie (3.12)). Il fattore KI è noto come fattore di

intensificazione delle tensioni (SIF) per il modo di rottura I. L’intero stato di sollecitazione all’apice di una fessura è univocamente determinato nel momento in cui risulta noto il fattore dimensionale KI. che definisce l’ampiezza della singolarità all’apice. Una volta noto questo fattore

Figura 3.10 Stress normal to the crack plane in Mode I

L’utilizzo di un singolo parametro per caratterizzare gli effetti che una fessura ha su un dato componente è una delle principali prerogative della meccanica della frattura. La rottura avrà luogo allorquando KI raggiunge un valore critico KIC, parametro tipico del materiale in esame

ottenute da prove in stato piano di deformazione. In generale il fattore di concentrazione delle tensioni assumerà la seguente espressione:

(3.14) KI =FC

σ

π

a

in cui

F

_c è un fattore che dipende dalla geometria considerata (forma del difetto e sua posizione nel componente) e dalle condizioni di carico. Tramite l’espressione (3.14) è possibile correlare il fattore di intensificazione delle tensioni con il tasso di rilascio dell’energia elastica all’apice della fessura. Sostituendo la (3.14) nella (3.10) si ottiene:

(3.15)

(

)

       − = E K E K G I I I 2 2 2 1

ν

In letteratura sono disponibili diverse correlazioni del fattore di intensificazione in relazione alla forma del difetto, alla sua posizione nel componente in esame e alle condizioni di carico. Per una fessura semiellittica superficiale, che generalmente è presa in considerazione in fase di progetto nella normativa ASME III per la verifica di un componente alla fessurazione, le correlazioni più attendibili sono risultate quelle di Raju & Newman. Su risultati ottenuti agli elementi finiti riuscirono ad ottenere correlazioni empiriche che fossero in grado di descrivere lo stato di sollecitazione lungo il fronte della fessura semiellittica (APPENDICE B).

Plane Stress

La determinazione dello Stress Intensification Factor può essere eseguita tramite il metodo della Weight Function. Tale metodo è basato sul principio di sovrapposizione e vale unicamente nell’ambito della meccanica della frattura lineare elastica. Il metodo deriva dall’osservazione che differenti condizioni di carico possono determinare lo stesso SIF.

Se le equazioni sono lineari possiamo immaginare lo schema di sovrapposizione degli effetti evidenziato nella precedente Figura. Come si nota nella immagine (b) la cricca può essere virtualmente eliminata applicando ai lembi il carico di compressione s; tale carico (nella zona in cui si trova il difetto) è uguale e di segno opposto al carico applicato alla piastra senza cricca (immagine (a)); quest’ultimo carico è detto “carico o tensione nominale”. Si noti che per le due piastre le condizioni al contorno sono le stesse. Il metodo prevede quindi che il valore del KI possa

essere determinato con una relazione del tipo indicato:

(3.16) K_I =

∫

2aH

( )

x a ⋅ x dx

0 ,

σ

( )

Nella relazione integrale

σ

( )

x è la tensione nominale e H ,

( )

x a è una opportuna funzione della sola geometria del difetto (in particolare della lunghezza a della cricca) denominata Weight Function (WF). Anche in questo caso esistono varie correlazioni in letteratura che consentono di definire lo stato di tensione all’apice di un difetto partendo dalla distribuzione effettiva della tensione nel componente integro, privo di fessure.

3.2.3 Plasticizzazione all’apice di una fessura.

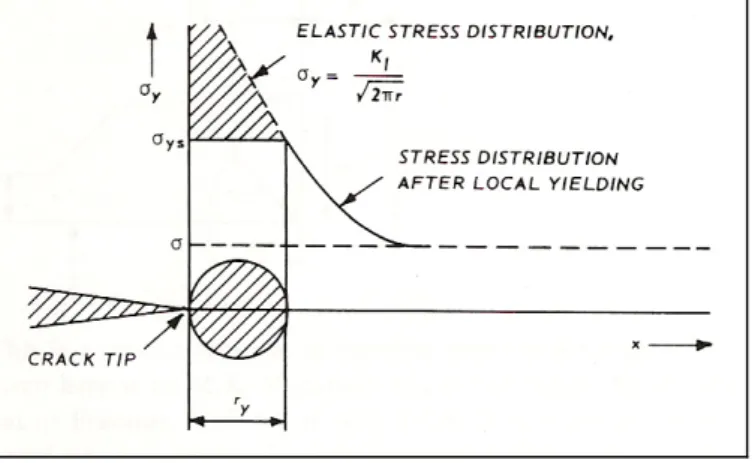
La soluzione elastica dello stato di tensione nella zona adiacente alla fessura mostra una discontinuità all’apice di essa. Le tensioni tendono all’infinito per r tendente a zero ma in realtà la tensione sarà limitata dalla tensione di snervamento del materiale. Pertanto si svilupperanno deformazioni plastiche all’apice della fessura tali da generare una completa ridistribuzione delle tensioni. E’ possibile arrivare ad una stima delle dimensioni di tale zona plastica considerando i

casi di stato piano di tensione e quello di deformazione prendendo a riferimento lo stato di tensione generato in direzione normale al piano contenente la fessura descritto dall’espressione (3.13).

Figura 3.11 A first approximation to the crack tip plastic zone

In condizioni di plane stress la condizione di snervamento si verifica nel momento in cui la tensione uniassiale di snervamento del materiale uguaglia la componente normale,

σ

_y

=

σ

_YS. Sostituendo la

σ

_YS nell’equazione (3.13) è possibile arrivare alla stima della distanza ry dall’apice

della fessura in cui la

σ

_y supera la tensione di snervamento.

(3.17) 2 2 1       = YS I y K r

σ

π

Se sono trascurabili gli effetti di incrudimento del materiale (comportamento elastico perfettamente plastico) la distribuzione delle tensioni per

r

≤

r

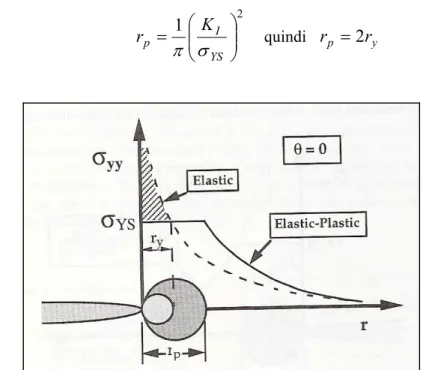
_y può essere rappresentata da una linea orizzontale in corrispondenza allo snervamento come illustrato in Figura 3.11. Dalla Figura si evince chiaramente che la procedura adottata non è rigorosamente corretta perché si fonda sull’assunzione di una soluzione elastica. Nel momento in cui si ha lo snervamento, le tensioni dovranno subire una ridistribuzione per soddisfare l’equazione dell’equilibrio globale sul componente. A seguito do ciò è chiaro che l’effettiva zona plastica dovrà essere più grande di ry dal momento che il carico

rappresentato dall’area tratteggiata in Figura 3.11. deve essere in qualche modo equilibrato. Questo può essere realizzato se si estende la zona plastica in corrispondenza dell’apice della fessura come mostrato in Figura 3.12. Un semplice bilancio di force porta alla stima dell’effettiva dimensione della regione plastica assunta di forma circolare in prima approssimazione:

(3.18)

=

∫

=

∫

y y r I r y p YS

dr

r

K

dr

r

0 0

2

π

σ

σ

da cui: (3.19) 2 1       = YS I p K r

σ

π

quindi

r

p

=

2

r

y

Figura 3.12 First-order and second-order estimates of plastic zone size

Riferendoci alla Figura 3.12, si può notare che la ridistribuzione della tensione nella zona elastica è più alta di quella predetta dall’equazione (3.13), richiedendo un più alto fattore di concentrazione delle tensioni, Keff. Irwin dimostrò che la plasticizzazione può essere considerata come un

incremento fittizio delle dimensioni della cricca, Figura 3.13. La plasticizzazione all’apice della cricca determina deformazioni maggiori e rigidezza minori rispetto al caso elastico, il componente strutturale si comporta come se essa contenesse una fessura di dimensioni maggiori rispetto a quelle reali. Irwin dimostrò che una buona approssimazione del Keff è ottenuta ponendo l’apice

dell’effettiva fessura considerata nel centro della regione di plasticizzazione. In definitiva la lunghezza effettiva della cricca risulta:

(3.20)

a

_eff

=

a

+

r

_y

il valore dell’effettivo fattore di intensificazione degli sforzi è ottenuto inserendo la dimensione effettiva della fessura nell’espressione generale (3.14):

(3.21)

K

_eff

=

F

_C

( )

a

_eff

σ

π

a

_eff

un processo iterativo sarà necessario per ottenere il valore esatto partendo dal SIF calcolato in assenza di plasticizzazione; tramite le equazioni (3.17) e (3.20) sarà possibile riaggiornale le

Figura 3.13 The Irwin plastic zone correction

In condizioni di stato piano di deformazione lo snervamento è raggiunto con uno stato triassiale di tensione e in definitiva la correzione della zona di plasticizzazione sarà più piccola di un fattore pari a tre:

(3.22) 2 6 1       = YS I y K r

σ

π

Per stimare la dimensione della zona in cui si ha la plasticizzazione del materiale all’apice del difetto si è considerato solo lo stato di tensione che si ha per θ = 0, lungo il piano della fessura. E’ possibile stimare l’estensione della regione plasticizzata per tutti i valori di angolo di inclinazione applicando un opportuno criterio di snervamento unito alle equazioni riportate nelle Tabelle 3.1-3.2. Consideriamo il classico criterio di Von Mises per definire i limiti della regione di snervamento:

(3.23)

[

(

_{1 2}

) (

2 _{1 3}

) (

2 _{2 3}

)

2

]

12

2

1

_σ

_σ

_σ

_σ

_σ

_σ

σ

e

=

−

+

−

+

−

dove,

σ

_e è la tensione equivalente e

σ

₁

,

σ

₂

,

σ

₃ sono le tre componenti principali del tensore degli sforzi. Secondo il criterio di Von Mises, lo snervamento ha inizio nel momento in cui è verificata l’uguaglianza tra

σ

_e

=

σ

_YS. Sostituendo, per esempio, lo stato di tensione del Modo I di rottura, riportato in Tabella 3.1, nell’equazione precedente e risolvendo in r, si ottiene la stima del raggio della zona snervata in funzione dell’angolo θ.

(3.24)

( )

    _{+ +}       =

θ

θ

σ

π

θ

2 2 sin 2 3 cos 1 4 1 YS I y K

(3.25)

( )

(

) (

)

    _{− + +}       =

ν

θ

θ

σ

π

θ

2 2 2 sin 2 3 cos 1 2 1 4 1 YS I y K

r per plane strain

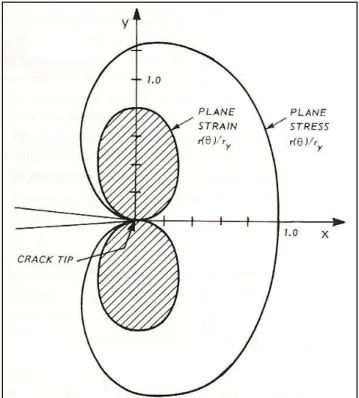
Le equazioni (3.24) e (3.25), rappresentate in Figura 3.14 e Figura 3.15, definiscono approssimativamente il confine tra il comportamento elastico e quello plastico del materiale. Le precedenti equazioni non sono tuttavia rigorosamente corrette perché si fondano su un’analisi puramente elastica non considerando la ridistribuzione delle tensioni.

Figura 3.14 Effect of thickness on plastic zone shape

3.3 Concetti base di meccanica della frattura elasto-plastica.

3.3.1 Il criterio energetico.

Per i materiali duttili è presente una deformazione plastica all’apice della fessura. Per questi materiali la propagazione di un difetto richiede la formazione di una zona plastica al nuovo apice. L’energia associata a tale plasticizzazione può essere considerata l’energia necessaria per la propagazione della fessura. Per questi motivi la resistenza alla fessurazione R è essenzialmente l’energia di deformazione plastica mentre il contributo di energia per la formazione delle superfici di frattura risulta praticamente trascurabile.

Se il fenomeno di frattura, invece, è accompagnato da notevoli deformazioni plastiche (come avviene per materiali molto duttili), non è più possibile effettuare un’ analisi di tipo elastico e bisogna far ricorso agli strumenti messi a disposizione dalla meccanica della frattura elasto-plastica (EPFM). In EPFM, il criterio di rottura del materiale è fornito da una relazione formalmente simile alla (3.11):

(3.26) H

σε

a =J_R

dove H è un fattore (detto funzione di influenza) che riveste lo stesso ruolo del termine

F

_c2

π

nell’equazione (3.11) (e dipende oltre che dalla geometria e dalle condizioni di carico anche dalle proprietà del materiale) e JR rappresenta la resistenza alla frattura del materiale. In EPFM, inoltre,

la forza motrice della fessura si indica con J anziché con G, per cui la relazione (3.26) può assumere la forma equivalente riportata di seguito:

(3.27) J = J_R

l’equazione (3.27) riveste lo stesso ruolo della (3.9).

Per poter impiegare l’equazione (3.27) in analisi di meccanica della frattura elasto-plastica, è necessario conoscere il legame esistente tra σ ed ε per il materiale in esame. In linea di principio, tale legame può essere descritto da qualsiasi relazione in grado di rappresentare l’andamento della curva sperimentale tensione-deformazione del materiale. Tuttavia, nella maggior parte dei casi, si effettua il fit della curva sperimentale ricorrendo ad una legge di potenza nota come legge di Ramberg-Osgood (R-O), (cfr. Paragrafo 3.3.3).

(3.28)

F

E

n

σ

σ

ε

=

+

A questo punto, sfruttando il legame tra tensioni e deformazioni fornito dalla relazione di R-O, è possibile riformulare il criterio di rottura fornito dall’equazione (3.26) nel modo seguente:

(3.29) _R n

J

a

F

H

a

E

H

a

H

σε

=

σ

2

+

σ

+1

=

Il primo termine a primo membro dell’equazione (3.29), rappresenta il contributo alla variazione di energia di deformazione dovuto alla parte lineare della curva tensione-deformazione (il confronto con l’espressione di G fornita dal primo membro della equazione (3.10), indica che nel caso elastico n=1, F=E’ e H =

π

F_C2), mentre il secondo termine a primo membro dell’equazione (3.29) rappresenta il contributo alla variazione di energia di deformazione dovuto alla parte non-lineare della curva tensione-deformazione. Tenendo conto della (3.10), la (3.29) diventa:

(3.30) _R n c

_J

F

a

H

E

a

F

=

+

+1 2 2

'

σ

πσ

In EPFM, il secondo termine a primo membro della (3.30) viene indicato con Jpl, dove pl sta ad

indicare la componente plastica del J, per cui la relazione precedente può essere riscritta nella forma seguente:

(3.31)

G

+

J

_pl

=

J

_R

Inoltre, è uso comune porre G=Jel, dove el sta ad indicare la componente elastica del J per cui

l’equazione (3.31) diventa:

(3.32)

J

_el

+

J

_pl

=

J

_R

Generalmente si pone J=Jel+Jpl. La relazione (3.31) costituisce il criterio di frattura impiegato in

EPFM. Tuttavia, per risolvere la (3.30), è necessario disporre di una relazione che descriva la tenacità alla frattura del materiale determinata generalmente per via sperimentale. Nel caso in cui Jel sia molto più piccolo di Jpl il primo termine dell’equazione (3.30) può essere trascurato e la

tensione di frattura può essere calcolata direttamente:

(3.33) ( )1 1 +













=

R n f

Ha

FJ

σ

mentre nel caso elastico risulta: (3.34) 2 1 2

'

















=

a

F

R

E

C f

_π

σ

in accordo al criterio energetico per materiale a comportamento puramente lineare (cfr. Paragrafo 3.3.1). I fattori geometrici FC e H, indispensabili per poter risolvere qualsiasi problema di

meccanica della frattura, si possono calcolare utilizzando opportune relazioni disponibili in letteratura. Il fattore geometrico elastico FC è stato calcolato per varie geometrie e condizioni di

carico e su espressioni sono riportate in vari manuali. Il fattore geometrico plastico dipende oltre che dalla geometria in esame e dalle condizioni di carico, dall’esponente n dell’equazione di R-O.

Per i materiali molto duttili, la resistenza alla frattura JR tende a crescere durante l’evolversi

del processo di frattura (Figura 3.16). Questo fatto consente l’avvio di fenomeni di frattura stabile, dato che la fessura è costretta ad arrestare la sua avanzata nel momento in cui la forza motrice diventa più piccola dell’energia necessaria alla frattura JR. La frattura può, quindi, crescere

lentamente e stabilmente fino al raggiungimento di una condizione critica in cui si verifica una propagazione rapidissima ed incontrollabile. Il fenomeno di crescita della frattura ha inizio nel momento in cui J = J_R. Perfino in EPFM il criterio energetico può essere opportunamente rappresentato per via grafica. Fissata la dimensione della fessura, è possibile disegnare una famiglia di curve variando la tensione σ nell’equazione (3.30), come illustrato nella seguente Figura.

Alla tensione σa il valore di J(a) è quello corrispondente al punto A. Quest’ultimo si trova più in

basso del punto B e quindi J risulta minore di JR. La frattura non può avanzare. Un innalzamento

della tensione al valore σi, porta J(a) al punto B. Adesso J=JR e la cricca può propagare. Ma essa è

stabile, dato che, se la tensione rimane pari al valore σi, J si porta in C e JR in D e l’avanzamento

della fessura deve arrestarsi. Affinché la frattura possa avanzare è necessario portare la sollecitazione a σb , in modo da spostare il valore di J(a) nel punto D. In questa fase la cricca cresce

stabilmente da a ad a+∆ab . Ulteriori incrementi di tensione comportano una crescita stabile della

cricca, per cui il processo di frattura risulta ancora sotto controllo. In questa fase è sufficiente mantenere la sollecitazione costante per scongiurare una rottura catastrofica del componente. Nel caso in cui, però, la sollecitazione raggiunga σfr , J(a) si porta in E e la frattura può propagarsi in

maniera instabile. Ad un ulteriore incremento della cricca, infatti, J continua a mantenersi più elevato di JR. La condizione di instabilità, quindi, si verifica nel momento in cui si raggiunge una

condizione di tangenza tra la curva J(a) e la curva JR :

(3.35)

( )

( )





















=













=

i i a R a i R i

da

dJ

da

dJ

a

J

a

J

Il sistema di equazioni (3.35) è frequentemente riportato in letteratura in una forma diversa. Moltiplicando ambo i membri della seconda equazione per E

σ

_YS2 , dove E è il modulo di Young del materiale e

σ

_YS è la tensione di snervamento, si ottiene:

(3.36)

da

dJ

E

da

dJ

E

R YS YS2

σ

2

σ

=

in cui, il primo membro viene comunemente indicato con Tapp, applied tearing modulus, mentre il

secondo con TR, dove il pedice R indica il valore di J sulla curva di resistenza alla fessurazione. In

Figura 3.17 viene schematicamente illustrata una tipica curva JR per materiali a comportamento non

lineare. Nei primi istanti della deformazione all’apice di un difetto, la curva R è pressoché verticale. Come aumenta il valore di J, il materiale all’apice inizia localmente a fessurarsi e il difetto avanza. Dal momento che l’andamento di R è monotono crescente, l’iniziale avanzamento del difetto è stabile ma condizioni di instabilità possono essere incontrati con incrementi di carico. L’indice di misura della tenacità a frattura, JIC, è definito in prossimità del punto di inizio crescita della

frattura. Questo indice ci fornisce alcune informazioni sul comportamento a frattura di un materiale duttile. La pendenza della curva ad un dato valore dell’estensione del difetto è un indice della

probabile una propagazione instabile della cricca. E’ proprio il fattore dimensionale TR a

quantificare la pendenza della curva di resistenza alla fessurazione.

Figura 3.17 Schematic J resistance curve for a ductile material

Le condizioni che governano la stabilità nei materiali elasto-plastici sono virtualmente identici al caso elastico presentato nel paragrafo 3.3.1. La instabilità si verifica nel momento in cui l’andamento della driving force J risulta tangente alla R-curve. La condizione di load control (la sollecitazione non diminuisce una volta che la frattura inizia a propagarsi) generalmente risulta meno stabile della condizione displacement control, dal momento che in quest’ultima situazione una crescita della fessura è accompagnata da una diminuzione dello stato di tensione e quindi può accadere che la forza motrice diventi minore della forza resistente JR causando l’arresto

dell’accrescimento della fessura.. In controllo di spostamento, quindi, il fenomeno di instabilità è influenzato anche dalle proprietà del sistema in esame. In definitiva la condizione di una propagazione stabile è espressa dalle seguenti relazioni:

(3.37) J =J_R e

T

_app

≤

T

_R

La propagazione instabile si verifica quando:

(3.38)

T

_app

>

T

_R

La curva JR è solitamente ricavata sottoponendo campioni del materiale in esame a prove di

Compact Tension. Essa può essere convenientemente schematizzata utilizzando la legge di potenza seguente:

(3.39)

( )

m IC R

r

a

C

J

a

J











 ∆

+

=

∆

dove: a

∆ è la variazione di lunghezza della cricca durante la fase di accrescimento;

IC

J

è la tenacità di inizio frattura;

m

C,

sono parametri ricavati da un fit dei dati sperimentali;

r

è un parametro di normalizzazione.

3.3.2 Il J-Integral.

Il tasso di rilascio di energia di deformazione in materiali a comportamento non lineare può essere univocamente identificato da un integrale di linea lungo un percorso qualsiasi che racchiude l’apice di una fessura. Rice fu il primo ad applicare il metodo di integrazione su un contorno a problemi di meccanica della frattura e giunse a dimostrare che quell’integrale, chiamato J, era per l'appunto il tasso di rilascio di energia in componenti ad elasticità non lineare contenenti difetti. Come vedremo nel seguente paragrafo il J è anche un parametro che caratterizza univocamente lo stato di tensione e deformazione, comportandosi come parametro di concentrazione delle tensioni.

Consideriamo il seguente integrale:

(3.40)

∫

Γ



_









∂

∂

−

=

ds

x

u

T

Wdy

J

i i essendo:

Γ

tracciato chiuso percorso in senso antiorario che racchiude l’apice della cricca (Figura 3.18 (A));

j ij

i

n

T

=

σ

la componente i-esima del tensore degli sforzi diretto secondo la normale esterna;

i

u

la componente i-esima del vettore spostamento;

ds un elemento infinitesimo del tracciato Γ;

∫

= ij

ij ijd

W ε

σ

ε

0 l’energia di deformazione per unità di volume.

Rice arrivò a dimostrare che il valore del J integral è indipendente dal tracciato di integrazione scelto attorno all’apice, basandosi sulla proprietà di J di essere nullo per ogni contorno chiuso Γ.

Figura 3.18 Contour integrals. (A) Elastic body; (B) Body with crack; (C) Path independence contour

Consideriamo un contorno chiuso ABCDEFA intorno all’apice di una fessura (Figura 3.18 (B)). Sui lati CD e FA, che costituiscono i lembi della cricca, il tensore T è nullo e dy=0 (il difetti si considerano appuntiti), pertanto il contributo di queste parti all’integrale risulta nullo. Il contributo di ABC=Γ1 deve essere uguale e contrario al contributo di FED=Γ2 ,per la proprietà suddetta

dell’integrale J. Ciò significa che se l’integrale J è calcolato su Γ1, il suo valore è identico a quello

ottenibile calcolandolo su Γ2 con direzione antioraria. Ossia

J

_Γ1

= J

_Γ2, l’integrale è indipendente

dal percorso, perché le estremità sono sui lembi della cricca (Figura 3.18 (C).

Nel caso di materiale a comportamento lineare elastico, il J integral può essere valutato considerando la soluzione elastica del campo di tensione all’apice della fessura. Rice dimostrò che il suddetto integrale è uguale al tasso di rilascio di energia elastica G.

(3.41)

da

dU

G

J

=

=

−

per il caso elastico il J può essere messo in relazione al fattore di intensificazione delle tensioni come nelle (3.15) per il Modo I di carico:

(3.42)

(

)

       − = E K E K J I I 2 2 2 1

ν

Plane Stress Plane Strain

L’integrale J è pertanto una relazione generalizzata del rilascio di energia dovuta alla propagazione della cricca ed è valido anche se c’è una apprezzabile plasticizzazione all’apice di essa. Infatti essendo J indipendente dal percorso di integrazione, questo può essere scelto convenientemente (ad esempio lungo gli spigoli del provino) in zone in cui la soluzione è certamente elastica. L’integrale J è uno strumento relativamente semplice per caratterizzare univocamente il comportamento di un materiale duttile in presenza di difetti e permette di definire in tal modo un criterio di stabilità o meno alla propagazione.

3.3.3 Stato di Tensione all’apice di una fessura.

Il parametro energetico J può essere usato anche per caratterizzare lo stato di tensione in prossimità di una fessura nei materiali elasto-plastici. L’utilizzo di questo parametro come un fattore di concentrazione delle tensioni è da attribuire a Hutchinson, Rice e Rosengren.

Per descrivere il comportamento non lineare dei materiali duttili assunsero una legge di potenza tra tensioni e deformazioni plastiche simile a quella mostrata nell’equazione (3.28) dove il primo termine a secondo membro rappresenta la componente elastica di deformazione

ε

_el (contributo elastico dovuto alla legge di Hook), mentre il secondo termine a secondo membro rappresenta la componente plastica

ε

_pl di deformazione. L’impiego dell’equazione (3.28) permette di ottenere dei fits accurati della curva sperimentale tensione-deformazione per materiali incrudenti. La legge di Ramberg-Osgood (R-O) costituisce un’estensione di tale legge che permette di modellare anche la regione plastica della curva tensione-deformazione. Nella legge R-O, la deformazione plastica del materiale è espressa dalla relazione seguente:

(3.43)

F

n pl

σ

ε

=

in cui il termine n è chiamato “strain hardening exponent”, F prende il nome di modulo plastico. L’equazione R-O è stata sviluppata per descrivere il legame esistente tra tensioni e deformazioni effettive del materiale; tuttavia tale relazione può essere utilizzata anche per descrivere il legame tra tensioni e deformazioni ingegneristiche purchè il campo di validità rientri nei limiti del valore massimo della tensione ingegneristica. In letteratura è possibile trovare forme diverse per l’equazione (3.28) di R-O [28]; di seguito si riporta l’espressione più comunemente utilizzata per descrivere il campo di tensione:

(3.44) n O O O      + =

σ

σ

α

σ

σ

ε

ε

in cui,

σ

_O è la tensione presa a riferimento che di solito è assunta pari a quella di snervamento,

YS

σ

;

ε

_O

=

σ

_O

E

;

α

è una costante adimensionale; n è l’esponente di deformazione plastica. Hutchinson, Rice e Rosengren dimostrarono che sia le tensioni che le deformazioni devono avere un andamento 1r in prossimità dell’apice di una fessura per garantire l’indipendenza dal tracciato considerato per il J-integral. Nelle vicinanze di un difetto, ben all’interno della regione plastica, le deformazioni elastiche sono trascurabili dato che il loro contributo alla deformazione totale è piccolo, in tal modo la relazione tra tensioni e deformazioni si riduce ad una semplice legge di potenza come la (3.44). Queste due condizioni implicano la seguente formulazione per tensioni e deformazioni all’apice: (3.45) 1 2 1 1 1 + +













=













=

n n ij n ij

r

J

k

r

J

k

ε

σ

dove, k1 e k2 sono costanti di proporzionalità. Per materiali a comportamento lineare elastico (n=1),

le equazioni (3.45) predicono la singolarità

1

r

, le formulazioni risultano pertanto consistenti con la teoria LEFM (cfr. Paragrafo 3.2.2).

La distribuzione effettiva delle tensioni e delle deformazioni è ottenuta applicando opportune condizioni al contorno. Le seguenti equazioni descrivono lo stato di sollecitazione e rappresentano il cosiddetto modello HRR:

(3.46)

σ

( )

θ

ασ

σ

σ

1

~

,

1 2

_I

_r

n

EJ

ij n n O O ij +

















=

(3.47)

ε

( )

θ

ασ

ασ

ε

₂ 1

~

n

,

r

I

EJ

E

ij n n n O O ij +

















=

in cui, In è una coctante di integrazione che dipende da n (Figura 3.19);

σ

~

ij e

ε

~

ij sono funzioni

dimensionali in n e θ (Figura 3.20).Questi parametri dipendono anche dallo stato di sollecitazione (es. plane stress o plane strain ). Le due equazioni precedenti descrivono la cosiddetta singolarità HRR. L’integrale J definisce l’ampiezza di questa singolarità caratterizzando completamente le condizioni all’interno della regione plastica, come il fattore di intensificazione delle tensioni per la

LEFM. Un componente strutturale con una piccola zona snervata presenta due zone a diverse andamento: uno nella regione elastica dove le tensioni variano come

1

r

e uno nella regione plastica dove le tensioni variano come

r

− n1( )+1 .

Figura 3.19 Effect of the strain hardening exponent on the HRR integration constant

Figure 3.20 Angular variation of dimensionless stress for n=3 and n=13

La singolarità HRR presenta la stessa apparente anomalia della singolarità LEFM: le tensioni tendono all’infinito per r tendente a zero. Le macroscopiche deformazioni all’apice della fessura provocano l’arrotondamento del difetto che riduce localmente lo stato di tensione triassiale. L’apice arrotondato della fessura è una superficie libera, per cui la componente x della tensione deve annullarsi. L’analisi che porta alla singolarità HRR si fonda sulla teoria delle piccole deformazioni e cade in difetto per deformazioni più grandi del 10%. La componente normale alla superficie contenente la fessura raggiunge il suo picco quando

x

σ

_O

J

è approssimativamente pari all’unità e diminuisce per x→0; la singolarità HRR non è più valida all’interno di questa regione

della fessura (Figura 3.21). In Figura 3.22 vengono schematicamente illustrati gli effetti della plasticizzazione sulle tensioni in prossimità dell’apice.

Figura 3.21 Blunting causes the stresses to deviate from the HRR solution

3.4 Implementazione agli Elementi Finiti.

3.4.1 Cenni sul codice strutturale MSC.Marc.

Nel presente lavoro di Tesi la modellazione agli elementi finiti dei problemi di meccanica della frattura è stata condotta con il codice strutturale MSC.Marc2001.

Il codice MSC.Marc, sviluppato dalla MSC.Software Corporation (Santa Ana, California, USA), è un codice tridimensionale che utilizza la tecnica degli elementi finiti per discretizzare un dominio solido di forma qualsiasi. Il metodo degli elementi finiti (FEM = Finite Element Method) consente di determinare la soluzione numerica approssimata di un sistema di equazioni differenziali mediante la risoluzione di un sistema di equazioni algebriche, solitamente lineari, equivalenti. Il metodo rappresenta un potente strumento di analisi strutturale che consente lo studio di strutture complesse comunque vincolate e caricate. Nel caso di un mezzo elastico, che occupa un determinato dominio, le incognite sono rappresentate dalle componenti di spostamento del generico punto del continuo, che devono soddisfare opportune equazioni differenziali all'interno del dominio (equazioni di equilibrio indefinite, equazioni di congruenza, legame costitutivo) e sul contorno (condizioni al contorno sugli spostamenti o sulle tensioni). Il dominio è suddiviso in un numero finito di sottodomini detti elementi finiti. Gli spostamenti incogniti sono calcolati in alcuni punti degli elementi (nodi) e approssimati in tutti gli altri mediante prefissate funzioni (di interpolazione o di forma).

Il programma MSC.Marc consente di effettuare varie tipologie di analisi, dalle più semplici (di tipo statico in campo elastico-lineare) alle più complesse (transitori dinamici non lineari, analisi di scambio termico o anaòisi accoppiatte termo-meccaniche). La tipica procedura da seguire per compiere un’analisi strutturale con il codice sono le seguenti:

- costruzione del modello solido;

- applicazione dei carichi, esecuzione del calcolo e ottenimento della soluzione; - analisi dei risultati.

Il Sistema Marc contiene una serie di programmi integrati che facilitano l’analisi di problemi in campo ingegneristico. Il codice si compone dei due seguenti programmi:

• Mentat • Marc

Questi programmi lavorano insieme per generare le informazioni geometriche che definiscono la nostra struttura, eseguire l’analisi richiesta e rappresentare graficamente i risultati ottenuti (Figura 3.23).

Figura 3.23 The Marc System

3.4.2 Valutazione del J-Integral con il codice MSC.Marc.

Il codice MSC.Marc consente la valutazione del J-Integral attraverso due differenti procedure. Il primo metodo valuta l’integrale J proposto da Rice usando il metodo di Parks. Il secondo metodo propone una versione estesa del J-Integral formulata da Kishimoto e DeLorenzi. MARC valuta l’integrale J calcolando la variazione di deformazione plastica dovuta allo spostamento nodale che accade nel corso dell’analisi numerica. Diversi valori di questo parametro possono essere ottenuti scegliendo opportunamente diversi tracciati. Anche le deformazioni plastiche sono incluse nella valutazione della variazione di energia di deformazione in un analisi elasto-plastica, ciò permette di calcolare il J-Integral per un materiale a comportamento non lineare. Un alto livello di accuratezza nei risultati può essere raggiunto con una modellizzazione ad elementi finiti piuttosto grossolane in quanto il modello implementato nel codice si fonda sull’energia di deformazione degli elementi e non sui valori locali di tensioni e spostamenti. In un’analisi elasto-plastica il J-Integral sarà valutato al di fuori della regione di plasticizzazione e coinciderà con il tasso di energia liberata nella propagazione della fessura.

Il calcolo del J-Integral nel codice MARC si fonda sullo spostamento nodale e sulla differenziazione numerica per valutare la variazione di energia potenziale come funzione della posizione dei singoli nodi. Viene assunto che i carichi non cambiano durante lo spostamento nodale, quindi l’energia di deformazione risulta:

(3.48)

∑ ∫ ∫

+

=

elemets t V e ij ij n

dvdt

E

0 ₁

ε

σ

_&

(3.49)

∑ ∫ ∫

∑ ∫ ∫

+ +

+

=

elements t e ij V ij elements t V N N ij ij

dV

dV

dv

d

d

dv

d

u

d

d

dE

n n 0 0 ₁

l

₁

l

l

σ

ε

β

σ

Questa densità di energia è valutata tramite una differenziazione numerica a ciascun incremento per ogni spostamento nodale con l’obiettivo di ricavare il tasso di rilascio di energia dopo ogni passo temporale come: (3.50) t t t d dE d dE d dE       −       =       ∆ ∆ + l l l

il valore così ottenuto viene divise per la variazione dell’area di superficie della fessura, ottenendo in tal modo il valore del J-Integral.

Figura 3.24 Closed Contour Used in the Evaluation of the J-Integral

La formulazione classica del J-Integral proposta da Rice rappresenta un integrale curvilineo indipendente dal percorso di integrazione ed è equivalente, come sopra menzionato, al tasso di energia rilasciata in materiali a comportamento lineare elastico. In due dimensioni è così definito (Figura 3.24): (3.51)

∫

(

)

Γ Γ       ∂ ∂ − + = d x u n n T W J ij i j 1 1

σ

dove, W è la densità di energia di deformazione, T è la densità di energia cinetica,

σ

_ij è il tensore delle tensioni e u₁ è il vettore spostamento.

Una formulazione estesa del J-Integral è stata proposta da vari autori, in particolare Kishimoto e DeLorenzi, con lo scopo di includere nell’espressione classica alcuni effetti come la deformazione plastica, le forze di volume, i carichi termici, le forze inerziali, gli spostamenti e le deformazioni macroscopiche. La tipica espressione estesa dell’integrale J, implementata nel codice MARC, è la seguente (Figura 3.25):

(3.52)

∫

∫

∫

(

)

_       ∂ ∂ − ∂ ∂ − − ∂ ∂ −       ∂ ∂ − = dv x x u u t da x u t da x u t Wn J _i j _i j _{i i} j _ij ij 0 1

ε

σ

ρ

_&&

Figura 3.25 Numerical Evaluation for J-Integral (Virtual crack advance)

La valutazione di questo integrale J in MSC.Marc [29] è basata sul metodo del dominio di integrazione. Una valutazione diretta dell’equazione (3.52) non è affatto semplice in un’analisi agli elementi finiti per le difficoltà nel definire il tracciato Γ di integrazione. Nel metodo del dominio di integrazione, caso bidimensionale, l’integrale di linea è convertito in un integrale superficiale sull’area racchiusa dal tracciato. In due dimensioni, la formulazione del J-Integral assumerà la seguente forma: (3.53)

∫

Ω













∂

∂

−

∂

∂

∆

−

=

dv

x

u

W

x

x

a

J

_{j ij} j j 1 1 1

1

δ

_δ

_σ

Formulazione classica (3.54) Formulazione estesa

(

)

_∫

∫

∫

Γ Ω Ω ∂ ∂ ∆ ∂ −         ∂ ∂ − ∂ ∂ − ∆ ∂ −       ∂ ∂ − ∂ ∂ ∆ − = S da x u t a x dv x x u u f a x dv x u W x x a J j ij j i i j ij ij i j j 1 1 1 0 1 1 1 1 1 1

δ

_δ

_σ

_ρ

_σ

ε

&&

In tre dimensioni l’integrale di linea diventa un integrale di superficie mentre quello di area diventa un integrale di volume valutato su tutti gli elementi finiti racchiusi all’interno del dominio. Il codice MARC richiede la definizione delle regioni rigide per eseguire il calcolo del J-Integral. Tali regioni sono definiti dai set di nodi che contengono una parte del fronte della fessura e il contributo all’integrale sarà dato da tutti quegli elementi che hanno almeno un nodo in queste regioni.

3.4.3 Caratteristiche della Mesh da impiegare in FEM.

La principale difficoltà nell’analisi agli elementi finiti di problemi di meccanica della frattura è la capacità di ottenere una soluzione attendibile in prossimità dell’apice di una fessura. La mesh in questa zona deve essere opportunamente modellata in maniera tale da approssimare con sufficiente accuratezza le singolarità ivi presenti sulle tensioni e le deformazioni. Le singolarità all’apice devono essere ricavare a seguito di un’analisi “small-strain”. Sono stati concepiti molti metodi per ottenere una buona approssimazione ma comunque il metodo più diffusamente usato nelle modellazioni agli elementi finiti è il cosiddetto “1/4 point node technique” [31]. Se r è la distanza dall’apice di un difetto, le singolarità sulle deformazioni ottenute da un’analisi alle piccole deformazioni sono:

-

ε

∝ r−12 per materiale a comportamento lineare elastico;

-

ε

∝ r−1 per materiale a comportamento elastico perfettamente plastico;

-

_∝

−n+1

n

r

ε

per materiale incrudente con opportuna legge di potenza.

In due dimensioni le singolarità possono essere costruite agli elementi finiti usando elementi isoparametrici quadrilateri collassati all’apice a formare una specie di anello intorno alla fessura. Uno spigolo dell’elemento isoparametrico ad 8 nodi sarà collassato in maniera che tutti i suoi tre nodi –a,d,c- abbiano la stessa posizione geometrica all’apice mentre in nodi in mezzeria sugli spigoli connessi all’apice devono essere mossi ad 1/4 verso lo spigolo (Figura 3.26).

Questa procedura consente di ottenere una singolarità sulle deformazioni così espressa:

(3.55) ₁₂

r

B

r

A +

→

ε

per r →0 La singolarità −n+1 n

r non può essere ricreata esattamente ma un’opportuna combinazione dei due termini

r

−1 e

r

−12 può portare ad una sua buona approssimazione.

La prima singolarità r si ottiene imponendo che i tre nodi sopra citati abbiano gli stessi spostamenti ed adottando la tecnica del “quarter point” (A=0) (Figura 3.27 (a)).

La seconda singolarità 1 r si ottiene lasciando i nodi nella posizione di mezzeria e consentendo un movimento indipendente dei tre nodi collassati all’apice (B=0) (Figura 3.27 (b)).

La terza singolarità, come già definito in precedenza, può essere ottenuta con buona approssimazione utilizzando la tecnica del “quarter point” e permettendo ai nodi all’apice un movimento indipendente. In combinazione a questa tipologia di schematizzazione agli elementi finiti deve essere impiegata un’opportuna legge di potenza per descrivere il comportamento incrudente del materiale (in genere si utilizza la relazione di Ramberg-Osgood).

Figura 3.26 Collapsed two-dimensional element

Figura 3.27 Crack tip elements for elastic and elastic-plastic analysis

In tre dimensioni vengono generalmente utilizzati elementi isoparametrici tetraedrici a 20 nodi con una faccia collassata sul fronte della fessura (Figura 3.28). Le procedure per ottenere le singolarità in prossimità del difetto sono del tutto simili a quelle già viste per il caso bidimensionale. La mesh lungo il fronte della fessura è tipicamente creato a partire da una mesh piana con una tipica forma a ragnatela concentrata sull’apppice del difetto che viene estrusa lungo il fronte stesso. Questa procedura di modellizzazione agli elementi finiti consente di creare una regione rigida regolare che garantisce una buona accuratezza dei risultati ottenuti.

Figura 3.28 Collapsed three-dimensional element

Le dimensioni degli elementi focalizzati all’apice di una cricca influenzano l’accuratezza delle soluzioni che si possono ottenere. In linea di principio una più piccola dimensione radiale degli elementi porterà ad avere sempre più buoni risultati. Un’analisi di sensitività della mesh, infittendo opportunamente il modello agli elementi finiti in prossimità del difetto, dovrà essere