Alma Mater Studiorum
·
Università di Bologna
Scuola di Scienze
Dipartimento di Fisica e Astronomia Corso di Laurea in Fisica
Probabilità e Integrali di Percorso
Relatore: Presentata da:
Prof. Fiorenzo Bastianelli Matteo Vincenzi
1
Abstract
In questo elaborato tratteremo principalmente il concetto di Integrale di Percorso e come si applichi alla Meccanica Quantistica. In particolare seguiremo il modus operandi di Feynman e Hibbs, cercando quindi di evidenziare uno dei maggiori vantaggi di questo processo di calcolo, ossia la capacità di prestarsi bene all’analisi delle leggi fisiche che governano i fenomeni, più che alla loro interpretazione matematica. Inizieremo studiando la variazione nel concetto di probabilità di un evento tra la Fisica Classica e la Meccanica Quantistica. Poi procederemo introducendo l’Integrale di Percorso, che è una notazione particolare del concetto di Somma su tutti i percorsi, e mostrando alcune sue applicazioni semplici. Termineremo infine cercando di illustrare come i risultati a problemi quantistici ottenuti con gli Integrali di Percorso si riconducano a quelli ricavati partendo dall’Equazione di Schroedinger.
2
Indice
Introduzione 3
1 Analisi del concetto di probabilità 4
1.1 Probabilità di un evento quantistico . . . 4
1.2 Procedimenti di misura . . . 5
1.3 Cenni sul calcolo dell’ampiezza di probabilità . . . 6
2 Integrali di Percorso 9
2.1 Kernel e Somma su tutti i percorsi . . . 9
2.1.1 Limite Classico . . . 10
2.1.2 Somma su tutti i percorsi . . . 11
2.2 Integrali di Percorso . . . 12
2.2.1 Composizione del Kernel di più eventi . . . 13
2.3 Applicazioni semplici . . . 15
2.3.1 Particella libera . . . 16
2.3.2 Oscillatore armonico unidimensionale . . . 18
2.3.3 Effetto Aharonov-Bohm . . . 22
3 Problema di Schroedinger 25
3.1 Funzione d’onda ed Equazione di Schroedinger . . . 25
3.2 Problema di Schroedinger e Kernel . . . 28
3.2.1 Problema dell’oscillatore armonico . . . 29
Conclusioni 32
Appendice A 33
3
Introduzione
Gli Integrali di Percorso introdotti da Feynman e Hibbs rappresentano un processo per calcolare la probabilità associata a un evento quantistico, in particolar modo si riferiscono al moto di una particella da un punto 𝑎 a un punto 𝑏. Siccome le leggi che governano il mondo quantistico sono probabilistiche non è possibile utilizzare le tecniche classiche, che si riferiscono a eventi deterministici, per calcolare la probabilità di un evento, bensì è necessario sviluppare un processo che contempli il fatto che tutti i possibili esiti dell’evento contribuiscono con pesi diversi alla probabilità totale che l’evento si verifichi.
Ripercorreremo i passi di Feynman e Hibbs e tratteremo gli Integrali di Percorso iniziando dallo studio dell’esperimento delle due fenditure di Young, in particolare analizzando il concetto di probabilità in ambito quantistico e il suo calcolo; definiremo in generale quali siano i requisiti necessari affinché si possa calcolare la probabilità di un evento quantistico, come la figura di Interferenza di un fascio di particelle.
A seguire svilupperemo una tecnica più adeguata per computare la probabilità totale di un evento, ossia la Somma sopra tutti i Percorsi, la quale consiste nel sommare i contributi di tutte le possibili traiettorie che una particella può percorrere nel corso di un evento, che in genere possono essere infinite. La Somma sopra tutti i percorsi tuttavia, per come la definiremo, è legata ad assunzioni particolari le quali la rendono applicabile solo a un numero limitato di casi. Di conseguenza generalizzeremo questo concetto in quello degli Integrali di Percorso, la cui validità non dipende tanto dal metodo con cui li si calcola, quanto dal loro significato fisico. Questo è uno dei loro maggiori vantaggi, infatti si prestano bene a uno studio sul significato delle leggi fisiche per i vali fenomeni, pagando il prezzo di un minor rigore matematico; è inoltre un aspetto degli Integrali di Percorso su cui porremo più volte attenzione quando mostreremo delle applicazioni. Calcoleremo gli Integrali di Percorso per i modelli ideali della particella libera e dell’oscillatore armonico unidimensionale; inoltre mostreremo come effetti puramente quantistici, in particolare l’effetto di Aharonov-Bohm, possono essere spiegati facendo uso degli Integrali di Percorso.
Infine introdurremo l’Equazione e la funzione d’onda di Schroedinger. Cercheremo di dimostrare che partendo dagli Integrali di Percorso siamo in grado di ricondurci ai risultati del problema agli autovalori di Schroedinger, in particolare tratteremo il problema agli autovalori per l’oscillatore armonico unidimensionale.
4
Capitolo 1
Analisi del concetto di probabilità
In questo Capitolo condurremo un’analisi sul concetto di probabilità dell’esito di un esperimento fisico, in particolare inizieremo dalla sua definizione nell’ambito della Fisica Classica per poi approdare alla Fisica Quantistica. Considereremo, inoltre, similitudini e differenze tra i due ambiti con l’ausilio di alcuni esperimenti concettuali, descritti da Richard P. Feynman e Albert R. Hibbs in Quantum
Mechanics and Path Integrals, riguardanti possibili procedimenti di misura di un evento quantistico,
i quali ci permetteranno di sviluppare il concetto di Integrale di Percorso, che tratteremo nel Capitolo successivo.
1.1 Probabilità di un evento quantistico
La probabilità dell’esito di un evento in Fisica Classica può essere definita come il rapporto tra le occorrenze dell’esito stesso e la totalità degli esiti possibili, di modo che per un sufficiente numero di iterazioni dell’evento ci si possa attendere una frazione degli esiti attesi pari alla probabilità. Questa è la definizione di probabilità a noi più vicina, in quanto se ne può fare uso quotidianamente: basti pensare al singolo lancio di una moneta, per cui si trova immediatamente come, essendo “Testa” o “Croce” i soli due possibili esiti, la probabilità di ottenerne uno sia banalmente 1
2.
In Meccanica Quantistica questa definizione non varia, tuttavia il mondo a livello atomico e soprattutto le leggi che lo governano comportano una radicale e necessaria modifica delle metodologie di misura degli eventi, dovendo rinunciare a un approccio deterministico alla Fisica per adottarne invece uno statistico. Infatti osservabili che in Fisica Classica sono compatibili tra loro, per i quali cioè è possibile effettuare una misura simultanea del loro valore con precisione idealmente arbitraria, in Fisica Quantistica potrebbero non essere compatibili, come nel caso della posizione 𝑞 e dell’impulso 𝑝 di una particella. Quando questo accade non è più possibile sviluppare delle leggi che riescano a prevedere con certezza i valori dei due osservabili senza modificare irreversibilmente il fenomeno che si sta indagando; al massimo è possibile calcolare la probabilità associata ai possibili esiti dell’esperimento.
Una conseguenza di questo sostanziale cambiamento nella descrizione dei fenomeni è una sottile, ma importante, differenza nell’analisi degli esiti degli eventi e della loro probabilità. Tuttavia per il momento rimanderemo questo particolare confronto tra eventi classici e quantistici a paragrafi successivi, in quanto è prima necessario concentrarsi sulla definizione di alcuni procedimenti di misura concettuali. In questo modo sarà possibile comprendere meglio la natura statistica degli eventi quantistici e le successive definizioni della Somma su tutti i percorsi (o sum over all paths) e degli Integrali di Percorso (o Path Integrals), che tratteremo nel Capitolo 2.
5
1.2 Procedimenti di misura
Per poter definire la probabilità 𝑃 di un evento quantistico in un formalismo utile allo sviluppo del concetto di Integrale di Percorso consideriamo un’esperienza sull’interferenza degli elettroni, riportata sul Feynman-Hibbs. Supponiamo di avere una sorgente 𝑆 di elettroni preparati in uno stato con la medesima energia e che si propaghino isotropicamente nello spazio. Gli elettroni impattano successivamente una parete opaca 𝐶 con due fenditure 𝐹1 e 𝐹2 equidistanti dalla normale alla parete
passante per 𝑆, in modo che gli elettroni possano superare la parete soltanto attraversando le fenditure, che assumono il ruolo di sorgenti monofase e monoenergetiche di elettroni. A valle di 𝐶 sia uno schermo 𝐵 dotato di celle fotoelettriche, in modo che possa registrare con precisione idealmente arbitraria la posizione 𝑥 di arrivo degli elettroni su 𝐵 e la loro intensità, dove 𝑥 è la distanza tra il centro dello schermo e la cella che registra un elettrone.
I dati che osserviamo ci forniscono un profilo di interferenza analogo a quello che otterremmo da un esperimento di Young, quindi in prima analisi possiamo affermare che gli elettroni, come ci attendiamo, stiano manifestando un comportamento ondulatorio. Il profilo ottenuto in particolare ci rappresenta non solo l’intensità delle onde incidenti su una data cella in posizione 𝑥 di 𝐵, ma anche la probabilità di localizzazione degli elettroni in 𝑥; quindi abbiamo già la probabilità 𝑃 associata all’interferenza delle sorgenti in 𝐹1 ed 𝐹2. Proviamo ora a stabilire delle ipotesi per la sua
formulazione. L’ipotesi più “classica” che ci porterebbe ad affermare come un elettrone possa transire simultaneamente solo attraverso una delle due fenditure non è applicabile. Infatti se fosse vero allora la probabilità dell’evento di interferenza 𝑃 dovrebbe essere data dalla relazione 𝑃 = 𝑃1+
𝑃2, dove 𝑃1 e 𝑃2 sono rispettivamente le probabilità associate all’arrivo in 𝑥 di un elettrone che
transiti in maniera inequivocabile attraverso la fenditura 𝐹1 o 𝐹2. Il profilo di queste due probabilità
si può ottenere facilmente ostruendo l’una o l’altra fenditura e in particolare si osserva immediatamente come 𝑃 ≠ 𝑃1+ 𝑃2, dato che la loro somma non ci fornisce un profilo di
interferenza. Di conseguenza o la premessa che un elettrone non possa passare simultaneamente attraverso le due fenditure o la procedura per il calcolo di 𝑃 è incorretta.
Per fornire un’interpretazione più formale al risultato dell’esperimento e provare ad afferrarne le implicazioni introduciamo allora il concetto di ampiezza di probabilità (o Probability Amplitude). Siccome un elettrone, così come le altre particelle microscopiche, manifesta in certi esperimenti un comportamento ondulatorio possiamo descriverlo con una funzione d’onda, la cui ampiezza è rappresentata da un numero complesso 𝜙(𝑥) ≡ 𝜙, che definiamo come l’ampiezza di probabilità di arrivo in 𝑥. Con questo accorgimento, dato che stiamo interpretando l’intensità degli elettroni in 𝑥 come la loro probabilità 𝑃(𝑥) di arrivo nel medesimo, possiamo identificare 𝑃(𝑥) con il modulo quadrato dell’ampiezza di probabilità 𝜙. Nell’esperimento appena descritto allora otteniamo come:
𝑃 = |𝜙|2 (1.1)
𝜙 = 𝜙1+ 𝜙2 (1.2)
𝑃1 = |𝜙1|2 𝑃
2 = |𝜙2|2 (1.3)
dove con 𝜙1 e 𝜙2 indichiamo rispettivamente l’ampiezza di probabilità che l’elettrone arrivi in 𝑥
passando attraverso la fenditura 1 o 2.
Ricaviamo così come in generale 𝑃 ≠ 𝑃1+ 𝑃2, quindi come l’ipotesi “classica” che 𝑃 = 𝑃1+ 𝑃2, che
si ottiene considerando gli elettroni come particelle, sia incorretta; una conseguenza è che non possiamo affermare che un elettrone passi solo attraverso una fenditura, come farebbe appunto una particella classica. Se fosse questo il caso potremmo ottenere 𝑃 come la somma di due eventi separati, 𝑃1 e 𝑃2, mentre invece 𝜙1 e 𝜙2, che rappresentano i due possibili percorsi che potrebbe
6
prendere l’elettrone, si combinano linearmente, generando un’onda totale 𝜙 il cui modulo, e di conseguenza anche la probabilità associatavi 𝑃, è in generale diverso rispetto alla somma dei moduli singoli.
Di conseguenza l’elettrone non passa attraverso una sola delle fenditure ma parzialmente attraverso entrambe, secondo una modalità descritta dall’ampiezza di probabilità 𝜙, il cui modulo quadrato ci fornisce la probabilità di arrivo dell’elettrone in 𝑥 come riportato nelle Eq. (1.1)-(1.3).
Tuttavia si potrebbe porre la seguente argomentazione: “È stato ricavato che 𝑃 ≠ 𝑃1+ 𝑃2, ma 𝑃1 e
𝑃2 sono state ottenute chiudendo una delle due fenditure, quindi modificando grandemente la struttura dell’apparato sperimentale. In linea ipotetica potrebbe quindi essere possibile ricavare differentemente le espressioni di 𝑃1 e 𝑃2, cioè la probabilità associata al passaggio dell’elettrone
attraverso una delle due fenditure, evitando di apportare modifiche all’apparato che causino variazioni nell’esito dell’esperimento, in particolare la perdita del profilo di interferenza”.
L’antitesi a quest’argomentazione è ben nota: non è possibile. Infatti qualsiasi tentativo di preparazione di un apparato progettato per identificare attraverso quale fenditura l’elettrone passi, e abbastanza delicato da non deflettere l’elettrone in maniera sufficiente da distruggere il profilo di interferenza, deve fallire. Questa è una delle varie possibili enunciazioni del Principio di Indeterminazione di Heisenberg e non è mai stato verificato un esperimento in cui non fosse rispettato. Notiamo inoltre come si sposi bene con il Principio di Complementarità, il quale afferma che un fenomeno fisico non può manifestare nello stesso esperimento comportamenti particellari e ondulatori; nel nostro caso non possiamo allo stesso tempo avere un profilo di interferenza e sapere attraverso quale fenditura passi l’elettrone.
Continuiamo quindi a utilizzare il metodo per il calcolo delle probabilità delle Eq. (1.1)-(1.3), dato che rispetta i Principi qui sopra citata e spiega, almeno concettualmente, i risultati ottenuti dall’esperimento descritto in questo paragrafo.
1.3 Cenni sul calcolo dell’ampiezza di probabilità
Nel paragrafo precedente abbiamo enunciato il Principio di Heisenberg, il quale ci permette di giustificare l’affermazione che la probabilità 𝑃 di localizzazione dell’elettrone in un certo punto 𝑥 di uno schermo 𝐵 non può essere calcolata come la somma di due eventi separati 𝑃1 e 𝑃2 che
identificano univocamente attraverso quale delle due fenditure passi l’elettrone. Abbiamo quindi introdotto il concetto di ampiezza di probabilità 𝜙, che possiamo utilizzare per calcolare 𝑃 secondo le Eq. (1.1)-(1.3).
La definizione di 𝜙 non è tuttavia limitata all’esperimento di interferenza descritto sopra, è possibile infatti associare ad ogni possibile alternativa di un evento quantistico e non, sebbene in questo caso non sarebbe di grande utilità, un’ampiezza di probabilità. In particolare se stiamo considerando fenomeni manifestanti proprietà particellari allora diciamo che le ampiezze di probabilità sono associate a delle “alternative esclusive”, in quanto l’osservazione di una di esse implicherebbe inequivocabilmente che solo l’evento associato a quell’ampiezza si verifichi: è questo il caso di 𝜙1 e
𝜙2, che abbiamo per l’appunto definito come le ampiezze di probabilità associate ai due percorsi alternativi, da 𝐹1 a 𝑥 con 𝐹2 chiusa e da 𝐹2 a 𝑥 con 𝐹1 chiusa, che potrebbe intraprendere l’elettrone, che quindi se passa per 𝐹1 non può passare per 𝐹2 e viceversa; analogo è il caso del “Testa” o “Croce”, se un lancio di moneta fornisce “Testa” non può allo stesso momento fornire “Croce”. Se invece stiamo considerando fenomeni manifestanti proprietà ondulatorie allora diciamo che le varie 𝜙 sono associate a delle “alternative interferenti”, in quanto più ampiezze possono verificarsi simultaneamente e in più possono essere interagenti tra loro: è questo il caso di 𝜙1 e 𝜙2 quando
7
entrambe le fenditure sono aperte e non si tenta di stabilire attraverso quale tra le due sia passato l’elettrone, infatti quello che otteniamo è un profilo di interferenza (esemplificativo dell’origine del nome “alternativa interferente”) in cui il singolo elettrone ha probabilità di localizzazione in 𝑥 descritta dalle Eq. (1.1)-(1.3).
In questo paragrafo, e in tutti i successivi, ci limiteremo a considerare esperimenti in cui ci siano “alternative interferenti” di un evento, dato che è su queste che il metodo per il calcolo delle probabilità introdotto nei primi paragrafi si applica, oltre che gli Integrali di Percorso. Generalizziamo allora l’Eq. (1.2) affermando che l’ampiezza di probabilità 𝜙 di un evento è data dalla somma delle ampiezze 𝜙𝑖 di tutte le possibili alternative con cui l’evento stesso può realizzarsi, cioè:
𝜙 = ∑ 𝜙𝑖
𝑖
(1.4)
Per ricavare l’ampiezza di un evento dobbiamo quindi associare ad ogni modo alternativo con cui l’evento può verificarsi un’ampiezza 𝜙𝑖; nel caso del moto di una particella questo si traduce
nell’associare ad ogni possibile percorso della particella una 𝜙𝑖.
Per capirlo meglio come assegnare una 𝜙𝑖 a un percorso consideriamo un esperimento concettuale
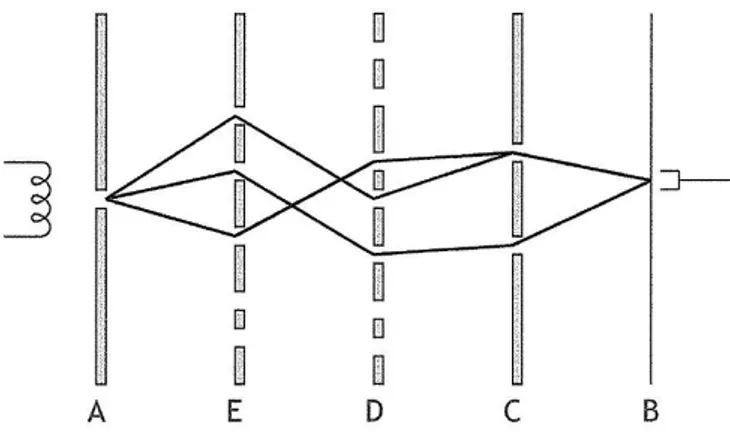
analogo a quello descritto nel paragrafo 1.1, aggiungendo alcuni elementi. Poniamo tra la sorgente, denominata 𝐴 in Fig. 1.1, e la parete con le fenditure 𝐶 delle pareti opache 𝐸 e 𝐷, le quali saranno progressivamente forate.
Fig. 1.1: Esperimento concettuale sulla definizione del percorso di una particella.
Osservando la figura uno si può notare come l’elettrone possa arrivare da 𝐴 a 𝐵 solo attraversando, nel seguente ordine, le fenditure in 𝐸, in 𝐷 e infine in 𝐶. Possiamo quindi identificare ogni fenditura con delle coordinate (𝑥, 𝑦), dove nella Fig. 1.1 𝑥 sarebbe sulle ordinate e 𝑦, che rappresenta la distanza delle pareti da 𝐴, sulle ascisse. In particolare l’elettrone può passare da una ogni fenditura in posizione (𝑥𝐸, 𝑦𝐸) sulla parete 𝐸 e per ognuna di queste può passare attraverso ogni fenditura in
(𝑥𝐷, 𝑦𝐷) sulla parete 𝐷; per ognuno di questi percorsi l’elettrone può passare attraverso l’una o l’altra
fenditura in (𝑥𝐶, 𝑦𝐶) su 𝐶 per poter poi giungere al rilevatore in ogni (𝑥𝐸, 𝑦𝐵) di 𝐵. Ciascuno di questi
percorsi alternativi ha un’ampiezza di probabilità associata e siccome sono un insieme numerabile possiamo, almeno idealmente, calcolarle separatamente per tutti i percorsi, sommarle ed ottenere la 𝜙 associata al moto da 𝐴 a 𝐵. Tuttavia questo procedimento non è praticabile, anche se il concetto alla base (calcolare la 𝜙𝑖 di ogni percorso e sommarla) è quello corretto. Immaginiamo di continuare
a forare 𝐸 e 𝐷 fino a quando non saranno scomparsi, in questo caso possiamo pensare alle nostre due pareti come all’unione di infinite fenditure di larghezza infinitesima; se poi aggiungessimo anche tanti schermi analoghi ad 𝐸 e 𝐷 allora potremmo pensare allo spazio tra 𝐴 a 𝐶 come all’unione di infiniti schermi distanti un infinitesimo l’uno dall’altro. Di conseguenza, attraverso questo processo
8
rudimentale di limite abbiamo trasformato le variabili 𝑥 e 𝑦 da discrete a continue. In particolare possiamo ora rappresentare i percorsi con funzioni, nel caso presente nella forma 𝑥(𝑦).
È ora evidente come calcolare separatamente l’ampiezza di tutti i possibili percorsi non sia applicabile: è necessario definire un nuovo metodo per calcolare le ampiezze di probabilità che sia più adatto alle esigenze matematiche della Meccanica Quantistica, dato che lavoreremo in questo ambito.
Ricapitolando, abbiamo definito il concetto di ampiezza di probabilità di un evento e il procedimento per il suo calcolo nell’Eq. (1.4), almeno nel caso che le possibili alternative dell’evento costituiscano un insieme finito e numerabile. Per il passaggio al continuo, brevemente introdotto in questo paragrafo, dobbiamo adottare nuovi concetti e nuovi metodi di misura che tratteremo nel Capitolo successivo.
9
Capitolo 2
Integrali di Percorso
Nel presente Capitolo ci concentreremo sulla definizione degli Integrali di Percorso e su alcune loro applicazioni basilari, al fine di calcolare la probabilità totale associata a un evento. In particolare per arrivare a sviluppare una formulazione per gli Integrali di Percorso ci baseremo sul concetto di ampiezza di probabilità riferito ad alternative interferenti, introdotto nel Capitolo 1, con il quale definiremo il Kernel e il procedimento di Somma su tutti i percorsi. Successivamente studieremo l’applicazione dell’Integrale di Percorso ai modelli ideali della particella libera e dell’oscillatore armonico, che a causa della loro relativa semplicità si prestano bene all’analisi di questo particolare metodo per il calcolo della probabilità di un evento, e alla spiegazione dell’effetto puramente quantistico di Aharonov-Bohm.
2.1 Kernel e Somma su tutti i percorsi
Nel paragrafo 1.3 abbiamo già descritto come sommare tutte le ampiezze di probabilità associate ai possibili percorsi per ottenere l’ampiezza totale di probabilità 𝜙 associata all’evento, tuttavia la forma presentata è ancora rudimentale ed è quindi necessario rifinirla e fornirle una veste matematica più appropriata prima di procedere con la definizione di 𝜙 per un evento generico. In particolare in questo paragrafo considereremo una generica particella che compia una certa traiettoria da un punto 𝑥𝑎 fisso, in cui si trova al tempo 𝑡𝑎, a un punto 𝑥𝑏 fisso, in cui si trova al tempo 𝑡𝑏; dove per semplicità
assumeremo che questa particella si muova in una dimensione.
Ragioniamo su alcune delle proprietà che dovrebbe avere 𝜙, per la singola traiettoria, dal punto di vista fisico per poi passare alla sua rappresentazione matematica. Se ci troviamo nell’ambito della Meccanica Quantistica, almeno per quanto riguarda il moto della particella, possiamo trascurare i processi di creazione e distruzione di particelle, e la Teoria dei Campi Quantizzati in generale, quindi possiamo pensare alle particelle che andremo ad analizzare come indistruttibili, anche se devono comunque manifestare comportamenti particellari e ondulatori. Per questo possiamo considerare ciascuna traiettoria come una funzione continua 𝑥(𝑡) della posizione rispetto al tempo; di conseguenza, dato che la 𝜙 è associata alla traiettoria, deve anch’essa essere continua in funzione del tempo. Una particella non può effettuare brusche variazioni nel suo moto, altrimenti subirebbe un’accelerazione infinita, che è impossibile; pertanto anche la derivata di 𝑥(𝑡) deve essere continua, così come quella di 𝜙. Per nostra definizione consideriamo il tratto di moto di una particella che inizia nel punto 𝑥𝑎 = 𝑥(𝑡𝑎) e finisce nel punto 𝑥𝑏 = 𝑥(𝑡𝑏), fissi, quindi la probabilità totale che la particella
percorra questo tratto è unitaria; di conseguenza l’ampiezza totale 𝜙𝑡𝑜𝑡 associata all’evento deve essere normalizzabile.
Le considerazioni appena elencate non sono esaustive ma contribuiscono a giustificare l’espressione dell’ampiezza 𝜙 qui riportata:
10
dove con la notazione 𝜙[𝑥(𝑡)] abbiamo enfatizzato l’appartenenza dell’ampiezza 𝜙 a una delle varie possibili traiettorie 𝑥(𝑡), con 𝑐 una costante di normalizzazione e con ℏ la costante ridotta di Planck. Nell’Eq. (2.1) abbiamo introdotto il termine 𝑆[𝑥(𝑡)] che rappresenta l’azione, una grandezza associata a ciascuna traiettoria, definita come
𝑆[𝑥(𝑡)] = ∫ 𝐿(𝑥̇, 𝑥, 𝑡)𝑑𝑡
𝑡𝑏
𝑡𝑎
(2.2) dove 𝐿 è la lagrangiana del sistema.
Per semplicità assumiamo che le traiettorie possibili dell’evento costituiscano un insieme finito e numerabile. Ridefiniamo così l’Eq. (1.4) e rinominiamo l’ampiezza di probabilità totale dell’evento, cioè una particella che si muove da un punto 𝑎 a un punto 𝑏, come Kernel, ottenendo la seguente equazione
𝐾(𝑏, 𝑎) = ∑ 𝜙[𝑥(𝑡)]
𝑝𝑒𝑟𝑐𝑜𝑟𝑠𝑖 𝑎−𝑏
(2.3)
In particolare, dato che abbiamo le traiettorie possibili sono alternative interferenti, possiamo applicare le regole per il calcolo della probabilità riportate nelle Eq. (1.1)-(1.3) e definire la probabilità totale dell’evento come
𝑃(𝑏, 𝑎) = |𝐾(𝑏, 𝑎)|2 (2.4)
Quello che cercheremo di sviluppare in questo Capitolo sarà quindi la definizione di metodi per calcolare 𝐾(𝑏, 𝑎), dato che è ciò che ci fornisce la probabilità totale di un evento.
Tuttavia queste formule sono presentate in una forma ancora inadeguata per la maggior parte delle situazioni in cui dovremo applicarle, secondo il ragionamento riportato al termine del Capitolo 1, quindi è necessario definire dei metodi di calcolo migliori. L’Eq. (2.3) per il Kernel in particolare è quella che presenta più problemi ed è perciò necessario che sia riscritta in una forma più corretta, per quanto il concetto alla base sia effettivamente quello che stiamo cercando: un metodo per sommare tutte le ampiezze possibili di un evento, dove queste contribuiscono all’ampiezza totale ciascuna con una certa fase: con l’attuale definizione di 𝜙[𝑥(𝑡)] identifichiamo questa fase con il termine all’esponente dell’Eq. (2.1), il quale è proporzionale all’azione 𝑆[𝑥(𝑡)], e che ci fornisce quanto una data ampiezza sia più o meno probabile rispetto a un’altra.
2.1.1 Limite classico
Al fine di controllare la validità dell’Eq. (2.1) per l’ampiezza consideriamo il suo comportamento quando ci poniamo nell’ambito classico.
Ogni ampiezza contribuisce con una fase proporzionale a 𝑆[𝑥(𝑡)] secondo la costante 1/ℏ; di conseguenza 𝑆 deve essere dell’ordine di ℏ se vogliamo che l’angolo della fase sia abbastanza piccolo da poterlo comparare con quello delle traiettorie vicine.
Consideriamo ora il Principio di Corrispondenza di Bohr, il quale enuncia che la Meccanica Quantistica deve concordare con la Meccanica Classica nelle condizioni in cui la Fisica Classica è nota fornire un’accurata descrizione dei fenomeni fisici; secondo questo principio l’espressione di 𝜙[𝑥(𝑡)] deve essere valida nell’approssimazione classica, cioè quando 𝑆 ≫ ℏ. In particolare l’ampiezza associata
11
alla traiettoria classica 𝑥̅(𝑡) deve essere fortemente predominante rispetto a tutte le altre, dato che per un fenomeno classico la traiettoria descritte dal corpo è univocamente determinata dalle condizioni iniziali del sistema. Ricaviamo la 𝑥̅(𝑡) dal Principio di Minima Azione, dove prendiamo 𝑥̅(𝑡) come una traiettoria ad estremi fissi che ci minimizza l’Azione e la variamo di un infinitesimo 𝛿𝑥(𝑡); espandendo poi al primo ordine l’azione, come riportata dall’Eq. (2.2), otteniamo:
𝑑 𝑑𝑡( 𝜕𝐿 𝜕𝑥̇) − 𝜕𝐿 𝜕𝑥= 0 (2.5)
la quale è la nota Equazione del Moto di Eulero-Lagrange che ci fornisce 𝑥̅(𝑡).
Tuttavia nell’approssimazione classica questa traiettoria non sembra essere privilegiata rispetto alle altre, andando apparentemente a violare il Principio di Corrispondenza. In realtà non è così: se effettuassimo su una traiettoria generica delle piccole variazioni 𝛿𝑥 in modo che manifestino degli effetti trascurabili in confronto all’azione, non sarebbero comunque trascurabili se considerate rispetto ad ℏ. L’angolo della fase, 𝑆/ℏ, è quindi enorme e se esprimiamo quest’ultima tramite le funzioni coseno e seno (rispettivamente per la parte reale e immaginaria) scopriamo come queste due funzioni oscillino rapidamente tra valori positivi e negativi, sotto variazioni 𝛿𝑥 sulla traiettoria. Di conseguenza il contributo totale delle ampiezze tende ad annullarsi; l’eccezione è proprio la traiettoria classica 𝑥̅(𝑡). Abbiamo ricavato 𝑥̅(𝑡) con il Principio di Minima Azione e quindi, per costruzione, se variamo 𝑥̅(𝑡) di 𝛿𝑥 non otteniamo cambiamenti in 𝑆, almeno al primo ordine; solo le traiettorie nelle vicinanze di 𝑥̅(𝑡) hanno associate ampiezze con fasi non troppo distanti e che quindi non si annullano a vicenda, quindi 𝑥̅(𝑡) risulta predominante rispetto a tutte le altre possibili traiettorie.
Otteniamo così come l’Eq. (2.1) dell’ampiezza 𝜙[𝑥(𝑡)] e di conseguenza anche le Eq. (2.3)-(2.4) rispettino il Principio di Corrispondenza di Bohr e abbiano quindi superato questa “prova del nove” sulla sua validità.
2.1.2 Somma su tutti i percorsi
Abbiamo introdotto con le Eq. (2.1)-(2.3) delle espressioni valide per esprimere l’ampiezza 𝜙[𝑥(𝑡)] e il Kernel 𝐾(𝑎, 𝑏), tuttavia non bastano a descrivere la complessità dei fenomeni quantistici; stiamo assumendo ancora che la totalità delle traiettorie possibili dell’evento sia un numero finito, che è una limitazione molto forte, come illustrato nel paragrafo 1.3. Per computare il valore di 𝐾(𝑎, 𝑏) nel caso, più fisicamente accurato, in cui infinite traiettorie possibili siano associate all’evento dobbiamo definire il processo di Somma su tutti i percorsi.
Possiamo farlo considerando una costruzione analoga a quella per l’integrale di Riemann. Sia 𝑓(𝑥) una funzione continua ed 𝐴 l’area ad essa sottesa; suddividiamo il dominio [𝑥𝑎, 𝑥𝑏] di 𝑓 in un insieme
di 𝑁 intervalli [𝑥𝑖, 𝑥𝑖+1], con 𝑖 = 0, … , 𝑁, tali che 𝑥𝑖+1− 𝑥𝑖 = 𝜖, con 𝜖 piccolo a piacere e con 𝑥0 =
𝑥𝑎 e 𝑥𝑁= 𝑥𝑏, e tali che ad ogni 𝑥𝑖 sia associata un’ordinata 𝑓(𝑥𝑖). Abbiamo quindi
approssimativamente suddiviso 𝐴 in 𝑁 sub-aree 𝐴𝑖 = 𝜖𝑓(𝑥𝑖), dove 𝜖 funge da fattore normalizzante,
di conseguenza operando il limite della somma delle 𝐴𝑖 per 𝑁 → +∞ otteniamo l’integrale di
Riemann:
𝐴 = lim
𝑁→+∞∑ 𝐴𝑖
12 = lim 𝑁→+∞𝜖 ∑ 𝑓(𝑥𝑖) 𝑖 (2.6) = ∫ 𝑓(𝑥)𝑑𝑥 𝑥𝑎 𝑥𝑎
Possiamo definire la Somma su tutti i percorsi con un procedimento analogo, partendo dal nostro caso: una particella che si muove da un punto 𝑥𝑎 = 𝑥(𝑡𝑎) a uno 𝑥𝑏 = 𝑥(𝑡𝑏), fissi. Prendiamo quindi
𝜙[𝑥(𝑡)] come la funzione continua 𝑓, così facendo l’area sottesa ad essa diventa 𝐾(𝑎, 𝑏); dividiamo il dominio temporale di 𝜙[𝑥(𝑡)] in 𝑁 intervalli [𝑡𝑖, 𝑡𝑖+1] tali che siano lunghi 𝜖 ed assegniamo ad ogni 𝑡𝑖 una posizione 𝑥𝑖; inoltre deve valere che 𝑡0 = 𝑡𝑎, 𝑡𝑁 = 𝑡𝑏 e 𝑥0 = 𝑥𝑎, 𝑥𝑁 = 𝑥𝑏, dato che sono punti fissi per condizione iniziale. Connettiamo ogni 𝑥𝑖 con delle linee, o con delle sezioni delle traiettorie
classiche per ogni intervallo se cerchiamo una maggiore accuratezza, così da poter integrare sui possibili valori di ogni 𝑥𝑖, ad eccezione di 𝑥0 e 𝑥𝑁 dato che sono fissi. In questo modo possiamo
esprimere l’ampiezza come:
𝜙[𝑥(𝑡)] = 𝑒ℏ𝑖𝑆[𝑏,𝑎,𝑥(𝑡)] (2.7)
dove 𝑆[𝑏, 𝑎, 𝑥(𝑡)] è l’azione associata alla traiettoria passante per ogni (𝑥𝑖, 𝑡𝑖), che per snellire la notazione indicheremo semplicemente con 𝑆[𝑏, 𝑎].
Inoltre abbiamo approssimativamente suddiviso 𝐾(𝑏, 𝑎) in 𝑁 sub-aree e se operiamo un processo di limite su 𝜖 analogo a quello per l’integrale di Riemann ricaviamo:
𝐾(𝑏, 𝑎) = lim 𝜖→0 1 𝐴∫ … ∫ ∫ 𝑒 (𝑖/ℏ)𝑆[𝑏,𝑎]𝑑𝑥1 𝐴 … 𝑑𝑥𝑁−1 𝐴 (2.8)
dove 𝐴−𝑁 è un fattore di normalizzazione dipendente da 𝜖 che è in generale molto complicato da trovare, anche perché non esiste una regola specifica per calcolarlo ma bisogna procedere caso per caso.
Il procedimento appena descritto è una Somma su tutti i percorsi e possiamo notare effettivamente come il contributo della fase di 𝜙[𝑥(𝑡)] cambi, per definizione, al variare dei punti (𝑥𝑖, 𝑡𝑖), i quali
sono integrati su tutto il dominio e quindi assumono tutti i valori possibili; di conseguenza stiamo considerando la totalità delle traiettorie e delle 𝜙[𝑥(𝑡)] possibili. Perciò con l’Eq. (2.8) otteniamo il risultato che stavamo cercando, infatti ci permette di calcolare il Kernel di un evento in cui il numero delle traiettorie possibili è infinito.
2.2 Integrali di Percorso
Nel paragrafo precedente abbiamo definito una Somma su tutti i percorsi tramite un’analogia con l’integrale di Riemann, tuttavia questo processo non si può applicare in tutti i casi. Per ipotesi abbiamo definito 𝜙 come continua anche nella sua derivata, per evitare che la velocità della particella considerata per l’evento sia discontinua, tuttavia nello sviluppo della Somma su tutti i percorsi non abbiamo rispettato questa condizione. Abbiamo suddiviso la traiettoria in coppie di punti (𝑥𝑖, 𝑡𝑖) che
abbiamo collegato tramite spezzate, o sezioni di traiettorie classiche, senza porre la continuità della derivata di 𝜙[𝑥(𝑡)] nei punti di congiunzione (𝑥𝑖, 𝑡𝑖). Per questo motivo il Kernel 𝐾(𝑏, 𝑎) calcolato
13
secondo l’Eq. (2.8) è in generale adatto soltanto nella situazione particolare in cui l’ampiezza di tutte le possibili traiettorie abbia la derivata continua in tutti i punti. Soltanto per i casi più semplici è quindi possibile calcolare 𝐾(𝑏, 𝑎) per mezzo di analogie con l’integrale di Riemann.
Prendiamo per esempio il caso in cui debba essere preso in considerazione il fenomeno di creazione e distruzione delle particelle, e in generale la Teoria dei Campi Quantizzati, allora non solo la derivata di 𝜙[𝑥(𝑡)] è discontinua ma anche 𝜙[𝑥(𝑡)] stessa, in quanto lo è anche 𝑥(𝑡). Chiaramente dobbiamo utilizzare un’altra Somma su tutti i percorsi rispetto a quella nell’Eq. (2.8), visto che avremmo molti punti di discontinuità nel dominio della traiettoria.
Un altro esempio è il caso in cui sia necessario considerare le leggi della Relatività Ristretta, come il vincolo superiore della velocità della luce per le velocità delle particelle massive; con questa limitazione la nostra particella non potrà più andare all’infinito spaziale e tornare in un tempo 𝜖 piccolo a piacere, come invece poteva prima, anche se solo ipoteticamente. O ancora consideriamo il caso in cui le particelle dell’evento siano soggette a un potenziale contenente delle singolarità, come i pozzi di Dirac.
Per tornare infine all’esempio iniziale, nel caso in cui la velocità della particella del nostro evento sia discontinua in almeno una coppia (𝑥𝑖, 𝑡𝑖), se la lagrangiana del sistema dipendesse dall’accelerazione allora non potremmo calcolarne l’Azione associata e di conseguenza la fase di 𝜙[𝑥(𝑡)]: si pensi anche solo a una particella soggetta a un potenziale centripeto.
È evidente che non possiamo limitarci all’analogia con l’integrale di Riemann ma dobbiamo definire la Somma su tutti i percorsi in una forma più generale, che non dipenda dal tipo di integrale utilizzato per portare avanti la Somma.
Definiamo allora Integrale di Percorso con la Somma su tutti i percorsi espressa nella forma:
𝐾(𝑏, 𝑎) = ∫ 𝑒(ℏ𝑖)𝑆[𝑏,𝑎]𝒟𝑥(𝑡) 𝑏
𝑎
(2.9)
dove 𝒟𝑥(𝑡) indica l’integrazione su tutto lo spazio delle funzioni {𝑥(𝑡)}, senza fare riferimento ad alcun particolare tipo di integrale.
Il processo di calcolo per la Somma su tutti i percorsi varia, tuttavia il suo significato non cambia: l’Integrale di Percorso calcola infatti il Kernel, il quale fornisce la probabilità 𝑃 di un evento che deve essere uno scalare; nel caso contrario significherebbe che la procedura portata avanti per ricavare 𝑃 sarebbe capace di influenzare lo stato fisico del sistema, che è assurdo. Solo il tipo di integrale con cui si porta avanti il calcolo dipende dal tipo di evento che si vuole analizzare.
Prima di fornire ulteriori considerazioni, anche in confronto agli esempi portati in questo paragrafo, procediamo a trattare alcune proprietà di base dell’Integrale di Percorso e ad analizzare alcune sue applicazioni basilari, che tratteremo nei paragrafi successivi.
2.2.1 Composizione del Kernel di più eventi
Finora abbiamo considerato un evento in cui una particella si muove tra due punti fissi 𝑎 e 𝑏 senza specificare alcun punto intermedio, infatti se determiniamo un punto 𝑐 attraverso cui transisce la particella allora anche questo diventa un punto fisso nel nostro evento. Tutte le traiettorie sono obbligate a passare da 𝑐 e sono quindi associate ad alternative in parte esclusive: il fatto che la particella passi dal punto 𝑐 esclude la possibilità che non ci passi, mentre tra 𝑎 e 𝑐 e tra 𝑐 e 𝑏 siamo nel caso solito di alternative interferenti. Dobbiamo perciò aggirare il problema dell’alternativa
14
esclusiva presentata dal punto 𝑐 che ci impedisce di applicare l’Integrale di Percorso, che abbiamo sviluppato a partire dalle sole alternative interferenti.
Il metodo più semplice è separare il nostro evento in due eventi, che denominiamo per brevità 𝑎 − 𝑐 e 𝑐 − 𝑏 e che rappresentano rispettivamente il moto della particella da 𝑎 a 𝑐 e da 𝑐 a 𝑏. Le Azioni associate agli eventi sono 𝑆[𝑐, 𝑎] e 𝑆[𝑏, 𝑐] e in particolare se poniamo la condizione 𝑡𝑎 < 𝑡𝑐 < 𝑡𝑏,
ossia che gli eventi si verificano successivamente nel tempo, otteniamo che:
𝑆[𝑏, 𝑎] = 𝑆[𝑏, 𝑐] + 𝑆[𝑐, 𝑎] (2.10) per come abbiamo definito l’Azione.
Sapendo questo vediamo come i due eventi sono in generale indipendenti l’uno dall’altro, sotto la condizione che lo stato fisico della particella in 𝑐 sia lo stesso per la stessa traiettoria: altrimenti vorrebbe dire che avremmo perso delle informazioni sull’evento al punto 𝑐; è una perdita che potrebbe succedere ma che vorremo evitare. Nonostante questo lo stato fisico della particella in 𝑐 può variare per traiettorie diverse, infatti 𝑐 non è un punto fisso e il suo stato fisico, e in particolare la sua posizione, non influisce sul modo in cui abbiamo definito gli eventi 𝑎 − 𝑐 e 𝑐 − 𝑏, come possiamo osservare dall’Eq. (2.10).
L’equazione per gli Integrali di percorso assume quindi la forma:
𝐾(𝑏, 𝑎) = ∫ 𝑒(ℏ𝑖)𝑆[𝑏,𝑐]+( 𝑖 ℏ)𝑆[𝑐,𝑎]𝒟𝑥(𝑡) 𝑏 𝑎 (2.11) Dato che gli eventi sono indipendenti possiamo separare l’esponenziale, integrando prima per l’evento 𝑎 − 𝑐 e calcolando successivamente il Kernel associato. In questo modo l’Eq. (2.11) diventa
𝐾(𝑏, 𝑎) = ∫ ∫ 𝑒(ℏ𝑖)𝑆[𝑏,𝑐]𝐾(𝑐, 𝑎)𝒟𝑥(𝑡)𝑑𝑥𝑐 𝑏 𝑎 +∞ −∞ (2.12) dove l’integrazione sulla posizione 𝑥𝑐 di 𝑐 garantisce che 𝐾(𝑐, 𝑎) sia l’ampiezza di probabilità totale dell’evento 𝑎 − 𝑐 per ogni valore di 𝑥𝑐, anche nel caso limite, e banale, in cui 𝑥𝑐 = 𝑥𝑎. Integrando poi per il secondo evento otteniamo l’espressione per il Kernel dell’evento originario 𝑎 − 𝑏:
𝐾(𝑏, 𝑎) = ∫ 𝐾(𝑏, 𝑐)𝐾(𝑐, 𝑎)𝑑𝑥𝑐 +∞
−∞
(2.13) dove considerazioni analoghe a quelle svolte per l’Eq. (2.12) ci garantiscono che 𝐾(𝑏, 𝑐) è l’ampiezza di probabilità totale dell’evento 𝑐 − 𝑏.
Il procedimento appena descritto si può facilmente generalizzare al caso di 𝑁 eventi successivi nel tempo. Assumiamo che lungo ogni traiettoria 𝑎 − 𝑏 possiamo identificare 𝑁 punti attraverso cui la particella passa, allora possiamo suddividere l’evento 𝑎 − 𝑏 in 𝑁 eventi, analoghi agli eventi 𝑎 − 𝑐 e 𝑐 − 𝑏, e dove ogni punto di congiunzione tra eventi successivi è etichettato con 𝑖 = 0, … , 𝑁 e posizionato in 𝑥𝑖, dove 𝑖 = 0 = 𝑎 e 𝑖 = 𝑁 = 𝑏. Similmente al caso di due eventi, possiamo trattare
questi 𝑁 eventi come indipendenti e quindi integrarli separatamente nell’espressione del Kernel dell’evento totale per poi procedere con l’integrazione su tutte le variabili 𝑥𝑖, escludendo 𝑥𝑎 e 𝑥𝑏
15 𝐾(𝑏, 𝑎) = ∫ … ∫ ∫ 𝐾(𝑏, 𝑁 − 1) … 𝐾(𝑖 + 1, 𝑖) … 𝐾(1, 𝑎)𝑑𝑥1… 𝑑𝑥𝑁−1 +∞ −∞ +∞ −∞ +∞ −∞ (2.14) Ogni Kernel 𝐾(𝑖 + 1, 𝑖) può essere espresso come un Integrale di Percorso e in particolare otteniamo che l’Eq. (2.14) può essere riscritta nella forma:
𝐾(𝑏, 𝑎) = ∫ 𝑒(ℏ𝑖)𝑆[𝑏,𝑁−1]+⋯+( 𝑖 ℏ)𝑆[𝑖+1,𝑖]+⋯+( 𝑖 ℏ)𝑆[1,𝑎]𝒟𝑥(𝑡) 𝑏 𝑎 (2.15) Per generalizzazione dell’Eq. (2.10), implicata quando abbiamo assunto che gli 𝑁 eventi considerati potessero essere considerati indipendenti, otteniamo immediatamente come l’Eq. (2.10) si possa ricondurre all’Eq. (2.9), che rappresenta il Kernel di un singolo evento.
Basandoci sull’Eq. (2.15), possiamo quindi affermare che le ampiezze di eventi successivi nel tempo si moltiplicano e che il Kernel per eventi successivi nel tempo può essere ricondotto al Kernel di un evento singolo. Notiamo però che questo non causa un problema per quanto riguarda i tipi di alternative a cui sono associate le nostre traiettorie: nel caso in cui esprimiamo 𝐾(𝑏, 𝑎) nella forma dell’Eq. (2.14) stiamo considerando ogni ampiezza dell’evento totale come composta da 𝑁 ampiezze a cui sono associate alternative interferenti; nel caso in cui riconduciamo 𝐾(𝑏, 𝑎) all’Eq. (2.9) stiamo considerando un evento singolo e quindi ogni ampiezza è associata ad alternative interferenti, la differenza con la formulazione precedente sta nella perdita di informazioni sulle posizioni intermedie che la particella può assumere nel corso dell’evento. Tuttavia in questo modo ci troviamo di fronte a un problema, infatti se stiamo considerando 𝑁 eventi successivi nel tempo allora stiamo implicando che al termine di ogni evento 𝑖 il sistema abbia un impatto abbastanza elevato sull’ambiente circostante da permetterne una sorta di identificazione, fosse anche solo il fatto che un evento è iniziato e poi terminato. Abbiamo visto che questi 𝑁 eventi sono riconducibili a un evento singolo, il quale non è caratterizzato da questi istanti successivi che separano i vari eventi, quindi la questione è la seguente: 𝑁 eventi successivi nel tempo subiscono dei minimi cambiamenti che gli permettono di essere distinguibili l’uno dall’altro, tuttavia il Kernel che forniscono è lo stesso di un singolo evento in cui questi cambiamenti sono assenti. Possiamo provare a risolverla considerando questa suddivisione in eventi come un semplice artificio matematico, tuttavia nel caso questo non fosse adeguato allora sarebbe conveniente modificare l’espressione dell’ampiezza di probabilità dell’evento; in particolare, come vedremo nel Capitolo 3, la funzione d’onda di Schroedinger è indipendente dal passato della particella e dalla successione di eventi che ha portato alla sua definizione.
Ritornando al caso corrente, possiamo ottenere che nell’assunzione che gli 𝑁 eventi si susseguano l’un l’altro con un intervallo di tempo 𝜖 piccolo a piacere possiamo ricondurre l’Eq. (2.14) non solo all’Integrale di percorso di un evento singolo, ma anche all’Eq. (2.8): entro le limitazioni in cui l’analogia con l’Integrale di Riemann è valida, possiamo calcolare il Kernel per eventi successivi nel tempo tramite l’Eq. (2.8), che può essere utile nel calcolo del Kernel per i modelli fisici più semplici.
2.3 Applicazioni semplici
Abbiamo introdotto gli Integrali di Percorso e alcune loro proprietà. In particolare, nel paragrafo precedente abbiamo stabilito come gli Integrali di Percorso associati ad eventi che si succedono nel tempo possono ricondursi all’Eq. (2.9), associata a un singolo evento, e inoltre abbiamo stabilito che in alcuni casi particolari si può svolgere l’Integrale di Percorso di un evento sfruttando delle analogie
16
con l’integrale di Riemann; possiamo in questi casi ricondurci all’Eq. (2.8), che può essere utile per i calcoli.
Procediamo quindi ad analizzare alcune applicazioni del concetto di Integrale di Percorso a sistemi fisici semplici, o comunque non così complicati da impedirne la trattazione in questa sede: questi saranno il modello della particella libera e il modello di un oscillatore armonico unidimensionale. Inoltre mostreremo anche come gli Integrali di Percorso possano spiegare l’effetto Aharonov-Bohm.
2.3.1 Particella Libera
Calcoliamo il Kernel per una particella libera che si muova da un punto 𝑎 a un punto 𝑏. Classicamente sappiamo che, per definizione del modello, la particella deve essere ferma o muoversi di moto rettilineo uniforme. Quantisticamente non possiamo stabilire in modo univoco il moto della particella a partire dalle stesse condizioni iniziali, infatti le traiettorie che compie non sono deterministiche ma descritte da leggi probabilistiche; in particolare le possibili traiettorie sono alternative interferenti l’una con l’altra e quindi possiamo trattare il problema utilizzando gli Integrali di Percorso.
Consideriamo dunque la lagrangiana classica associata al problema 𝐿 =𝑚
2 𝑥̇
2 (2.16)
Questa fa riferimento a una traiettoria singola, come è d’obbligo per l’ambito classico, tuttavia noi dobbiamo integrare su infinite traiettorie, quindi è conveniente esprimere la lagrangiana in una forma differente. Separiamo il percorso 𝑎 − 𝑏 in 𝑁 intervalli [𝑥𝑖−1, 𝑥𝑖] tali che 𝑥𝑖 = 𝑥(𝑡𝑖) e tali che ogni 𝑡𝑖
si verifichi dopo un intervallo temporale 𝜖 = 𝑡𝑖 − 𝑡𝑖−1, con 𝑖 = 1, … , 𝑁 e con 𝑥0 = 𝑥𝑎 e 𝑥𝑁 = 𝑥𝑏.
Abbiamo quindi diviso l’evento 𝑎 − 𝑏 in 𝑁 eventi che si susseguono nel tempo dopo un intervallo di tempo 𝜖. Inoltre se assumiamo che la particella non si muove a velocità relativistiche e se non consideriamo gli effetti della Teoria dei Campi Quantizzati allora ci poniamo nella condizione in cui è possibile calcolare l’Integrale di Percorso dell’evento con l’integrale di Riemann. Come ricavato nel paragrafo 2.2.1, possiamo calcolare il Kernel dell’evento 𝑎 − 𝑏 tramite l’Eq. (2.8) e in particolare, siccome la lagrangiana dell’evento si può separare in 𝑁 lagrangiane
𝐿𝑖 = 𝑚 2 ( 𝑥𝑖 − 𝑥𝑖−1 𝜖 ) 2 (2.17) otteniamo come l’Eq. (2.8) assuma la forma
𝐾(𝑏, 𝑎) = lim 𝜖→0 1 𝐴𝑁∫ … ∫ exp { 𝑖 ℏ 𝑚 2𝜖∑(𝑥𝑖− 𝑥𝑖−1) 2 𝑁 𝑖=1 } 𝑑𝑥1… 𝑑𝑥𝑁−1 (2.18)
dove 𝐴 è un fattore di normalizzazione dipendente da 𝜖 e dove la fase nell’esponenziale è stata ottenuta calcolando le Azioni 𝑆𝑖 associate alle 𝐿𝑖 e sommandole linearmente, con un processo e delle
considerazioni analoghi a quelli per l’Eq. (2.15). Prima di procedere con il calcolo del Kernel dobbiamo ricavare il valore di 𝐴 e per farlo possiamo applicare la seguente procedura formale, nella quale ci baseremo principalmente sul concetto dell’Integrale di Percorso in modo da capirne meglio il significato, anche se il calcolo richiederà così un maggiore livello di astrazione nei passaggi rispetto ad altri possibili procedimenti.
Siccome 𝐴 è lo stesso per tutte le variabili 𝑥1… 𝑥𝑁−1 e non dipende direttamente da 𝑁 ma solo da 𝜖,
per semplificare i calcoli ci basta porre 𝑁 = 1, in questo caso non stiamo quindi considerando una successione temporale di eventi ma un evento singolo che avviene in un intervallo di tempo 𝜖 piccolo
17
a piacere, dove questa condizione è necessaria per la validità del limite nell’Eq. (2.18); con queste accortezze l’evento corrisponde proprio a uno dei sub-eventi in cui abbiamo precedentemente suddiviso l’evento 𝑎 − 𝑏. Di conseguenza otteniamo che 𝑥0 = 𝑥𝑎 e 𝑥1 = 𝑥𝑏 e inoltre possiamo
definire una nuova variabile 𝜉 = 𝑥𝑏− 𝑥𝑎, che corrisponde all’intervallo spaziale in cui si verifica
l’evento; poniamo allora che 𝑥𝑎 sia fisso all’origine e 𝑥𝑏= 𝜉 possa tendere all’infinità spaziale, allora
il dominio di 𝜉 diventa [−∞, +∞].
Abbiamo imposto che l’evento può avvenire in tutto lo spazio, tuttavia questo è solo un limite formale per facilitare i calcoli, non riflette realmente una caratteristica dell’evento: dire che 𝜉 varia su tutto lo spazio significa ammettere che la particella può andare all’infinito in un tempo 𝜖 piccolo a piacere, e quindi dovrebbe avere una velocità infinita, che è assurdo. Questo limite ci semplifica di molto i calcoli, infatti ciò che abbiamo ottenuto con le semplificazioni apportate è la riduzione dell’Eq. (2.18) alla forma 1 𝐴 ∫ exp { 𝑖 ℏ 𝑚 2𝜖𝜉 2} 𝑑𝜉 +∞ −∞ = 1 (2.19)
dove abbiamo per il momento tralasciato il limite su 𝜖. Il valore unitario dell’equazione è dovuto al fatto che stiamo considerando la probabilità totale che durante l’evento la particella compia una traiettoria qualsiasi nello spazio: è chiaro che questa probabilità deve essere massima.
La seguente precisazione è necessaria: nel procedimento appena riportato ci siamo posti nel caso limite in cui 𝑁 = 1 e abbiamo operato altri trucchi in modo da ottenere il risultato banale che il contributo alla probabilità totale di un evento di una singola traiettoria è unitario; siamo in un caso limite e l’unica utilità di un Integrale di Percorso espresso in questa forma è di permettere un semplice calcolo di 𝐴. Procediamo quindi a integrare la gaussiana nell’Eq. (2.19) e poi risolviamo l’equazione. In questo modo otteniamo che
𝐴 = (2𝜋𝑖ℏ𝜖 𝑚 )
1/2
(2.20) che sostituito nell’Eq. (2.18) ci fornisce l’equazione per il Kernel
𝐾(𝑏, 𝑎) = lim 𝜖→0( 𝑚 2𝜋𝑖ℏ𝜖) 𝑁/2 ∫ … ∫ exp {𝑖 ℏ 𝑚 2𝜖∑(𝑥𝑖 − 𝑥𝑖−1) 2 𝑁 𝑖=1 } 𝑑𝑥1… 𝑑𝑥𝑁−1 (2.21)
A questo punto per calcolare 𝐾(𝑏, 𝑎) basta integrare separatamente su ogni variabile iniziando da 𝑥1
e procedere ricorsivamente. Tutti gli integrali sono integrali di gaussiane e quindi forniscono come risultato una gaussiana, di conseguenza è lecito portare avanti questo processo. L’integrale su 𝑥1 è:
( 𝑚 2𝜋𝑖ℏ𝜖) 2/2 ∫ exp {𝑖 ℏ 𝑚 2𝜖[(𝑥2− 𝑥1) 2+ (𝑥 1− 𝑥𝑎)2]} 𝑑𝑥1 (2.22) = ( 𝑚 2𝜋𝑖ℏ ∙ 2𝜖) 1/2 exp { 𝑖𝑚 2ℏ ∙ 2𝜖(𝑥2− 𝑥𝑎) 2}
Moltiplichiamo il risultato all’integrando rimanente e integriamo su 𝑥2, allora:
( 𝑚 2𝜋𝑖ℏ𝜖) 2/2 ∫ exp {𝑖 ℏ 𝑚 2𝜖[(𝑥3− 𝑥2) 2+(𝑥2− 𝑥𝑎) 2 2 ]} 𝑑𝑥2 (2.23) = ( 𝑚 2𝜋𝑖ℏ ∙ 3𝜖) 1/2 exp { 𝑖𝑚 2ℏ ∙ 3𝜖(𝑥3− 𝑥𝑎) 2}
18
Ripetiamo il procedimento per tutte le variabili e notiamo che per ogni 𝑥𝑗, con 𝑗 = 1, … , 𝑁 − 1 il
risultato dell’Eq. (2.22) diventa ( 𝑚 2𝜋𝑖ℏ ∙ 𝑗𝜖) 1/2 exp { 𝑖𝑚 2ℏ ∙ 𝑗𝜖(𝑥𝑗− 𝑥𝑎) 2 } (2.24)
Di conseguenza dopo 𝑁 − 1 iterazioni del procedimento e dopo aver effettuato il limite su 𝜖 → 0 ricaviamo 𝐾(𝑏, 𝑎) = ( 𝑚 2𝜋𝑖ℏ(𝑡𝑏− 𝑡𝑎) ) 1/2 exp {𝑖𝑚(𝑥𝑏− 𝑥𝑎) 2 2ℏ(𝑡𝑏− 𝑡𝑎) } (2.25) che corrisponde proprio al risultato che cercavamo: il Kernel per una particella libera che si muove da un punto 𝑎 a un punto 𝑏 percorrendo tutte le possibili traiettorie. Notiamo in particolare che 𝐾(𝑏, 𝑎) è indipendente dalla velocità o da altre condizioni iniziali della particella e che è dipendente solo dagli estremi delle traiettorie: per questo possiamo dire che il Kernel di una particella libera non dipende dal Sistema di Riferimento in cui la poniamo, a patto di restare sempre in condizioni non relativistiche; nel caso contrario dovremmo calcolare il Kernel con altri metodi.
2.3.2 Oscillatore armonico unidimensionale
Calcoliamo ora il Kernel per una particella che si muove da un punto 𝑎 a un punto 𝑏, fissi, il cui moto sia descrivibile come quello di un oscillatore armonico unidimensionale. Classicamente sappiamo che un oscillatore armonico deve essere periodico nel tempo di un periodo 𝑇 e che quindi una particella che passi per 𝑃, per ogni punto 𝑃 appartenente alla traiettoria classica, deve ritornare a passare esattamente per lo stesso punto dopo ogni periodo 𝑇. Quantisticamente invece non è così immediato definire un periodo per l’oscillatore armonico, infatti non possiamo determinare con precisione arbitraria la posizione di una particella senza modificare la natura del fenomeno in questione, come abbiamo già stabilito nel paragrafo 1.2 enunciando il Principio di Indeterminazione di Heisenberg: di conseguenza la particella non torna in un punto 𝑃 dopo un periodo, dato che non possiamo determinare l’esatta posizione di 𝑃. In questo caso quindi definiamo l’oscillatore armonico semplicemente con la sua lagrangiana
𝐿 =𝑚 2 (𝑥̇
2− 𝜔2𝑥2) (2.26)
dove 𝑥 rappresenta una traiettorie generica e dove 𝜔 = 2𝜋/𝑇 rappresenta la pulsazione dei modi normali dell’oscillatore ed è associato al potenziale armonico della particella, e dove quindi 𝑇 diventa il periodo dei modi normali dell’oscillatore e non più il periodo associato alla posizione della particella stessa.
Con queste accortezze possiamo affermare di stare considerando delle traiettorie associate ad alternative interferenti e quindi possiamo calcolare il Kernel con un Integrale di Percorso, per il cui computa utilizzeremo gli integrali gaussiani: integrali di percorso con le variabili agli esponenti al massimo al secondo ordine. Potremmo riapplicare il metodo utilizzato nel paragrafo precedente, tuttavia così facendo possiamo evidenziare un’altra caratteristica degli Integrali di Percorso.
Questo metodo è valido per lagrangiane nella forma 𝐿 = 𝑎(𝑡)𝑥̇2+ 𝑏(𝑡)𝑥̇𝑥 + 𝑐(𝑡)𝑥2 + 𝑑(𝑡)𝑥̇ +
𝑒(𝑡)𝑥 + 𝑓(𝑡), ma per il momento, al fine di facilitare il nostro calcolo, ci limiteremo a considerare un caso più simile alla nostra lagrangiana, che comunque non è restrittivo. Esprimiamo quindi l’Eq. (2.26) come
19 𝐿 = 𝑎(𝑡)𝑥̇2+ 𝑐(𝑡)𝑥2 (2.27) e l’Azione come 𝑆[𝑥(𝑡)] = ∫ [𝑎(𝑡)𝑥̇2+ 𝑐(𝑡)𝑥2]𝑑𝑡 𝑡𝑏 𝑡𝑎 (2.28) Consideriamo ora la traiettoria classica 𝑥̅(𝑡), che ci minimizza l’Azione, allora possiamo rappresentare tutte le traiettorie possibili come variazioni di 𝑥̅(𝑡); di conseguenza 𝑥 = 𝑥̅(𝑡) + 𝑦(𝑡), dove 𝑦(𝑡) è la deviazione dalla traiettoria classica. L’Eq. (2.28) assume perciò la forma
𝑆[𝑥(𝑡)] = ∫ [𝑎(𝑡)(𝑥̅̇2+ 2𝑥̅̇𝑦̇ + 𝑦̇2) + 𝑐(𝑡)(𝑥̅2+ 2𝑥̅𝑦 + 𝑦2)]𝑑𝑡 𝑡𝑏
𝑡𝑎
(2.29) ma dato che per costruzione 𝑦(𝑡𝑎) = 𝑦(𝑡𝑏) = 0 e 𝑥̅(𝑡) non porta modifiche all’Azione per variazioni
al primo ordine possiamo escludere i termini 2𝑥̅̇𝑦̇ e 2𝑥̅𝑦. Separiamo gli integrali in 𝑥 e 𝑦 e notiamo che quello in 𝑥 ci fornisce l’Azione classica, che denotiamo con 𝑆𝑐𝑙[𝑏, 𝑎]; di conseguenza l’Eq. (2.29)
assume la forma
𝑆[𝑥(𝑡)] = 𝑆𝑐𝑙[𝑏, 𝑎] + ∫ [𝑎(𝑡)𝑦̇2+ 𝑐(𝑡)𝑦2]𝑑𝑡 𝑡𝑏
𝑡𝑎
(2.30) che possiamo inserire nell’equazione del Kernel, e in particolare dato che 𝑑𝑥 = 𝑑𝑦 e 𝒟𝑥(𝑡) = 𝒟𝑦(𝑡) otteniamo che 𝐾(𝑏, 𝑎) = 𝑒ℏ𝑖𝑆𝑐𝑙[𝑏,𝑎]∫ 𝑒𝑥𝑝 {𝑖 ℏ∫ [𝑎(𝑡)𝑦̇ 2+ 𝑐(𝑡)𝑦2]𝑑𝑡 𝑡𝑏 𝑡𝑎 } 𝒟𝑦(𝑡) 0 0 (2.31) e quindi siccome 𝑦(𝑡𝑎) = 𝑦(𝑡𝑏) = 0 l’integrale nell’Eq. (2.31) può dipendere solo da 𝑡𝑎 e 𝑡𝑏 e allora
𝐾(𝑏, 𝑎) = 𝑒ℏ𝑖𝑆𝑐𝑙[𝑏,𝑎]𝐹(𝑡
𝑏, 𝑡𝑎) (2.32)
dove 𝐹(𝑡𝑏, 𝑡𝑎) è un fattore moltiplicativo, il cui calcolo è in generale non banale.
Questo procedimento non solo è applicabile nel caso di un oscillatore armonico ma anche ad altri casi la cui lagrangiana abbia variabili al massimo al secondo ordine, come per la particella libera. In particolare per il nostro oscillatore armonico otteniamo che
𝑆𝑐𝑙[𝑏, 𝑎] = 𝑚𝜔
2 sin[𝜔(𝑡𝑏− 𝑡𝑎)][(𝑥𝑏2+ 𝑥𝑎2) cos[𝜔(𝑡𝑏− 𝑡𝑎)] − 2𝑥𝑏𝑥𝑎] (2.33) per il cui calcolo rimandiamo all’Appendice A.
Per il calcolo di 𝐹(𝑡𝑏, 𝑡𝑎) è utile utilizzare il seguente procedimento, portato avanti tramite le serie di
Fourier, che in generale è valido anche in casi più complessi di questo.
Comparando l’Eq. (2.31) con l’Eq. (2.32) osserviamo che possiamo rappresentare 𝐹(𝑡𝑏, 𝑡𝑎) tramite
l’equazione 𝐹(𝑇) = ∫ 𝑒𝑥𝑝 {𝑖 ℏ∫ 𝑚 2(𝑦̇ 2− 𝜔2𝑦2)𝑑𝑡 𝑇 0 } 𝒟𝑦(𝑡) 0 0 (2.34) dove abbiamo posto 𝑡𝑎 = 0 e 𝑡𝑏 = 𝑇 per semplicità di calcolo.
Dato che 𝑦(0) = 𝑦(𝑇) = 0 possiamo scrivere la variazione 𝑦 rispetto alla traiettoria classica come una serie di Fourier con un periodo 𝑇
20 𝑦(𝑡) = ∑ 𝑎𝑛sin𝑛𝜋𝑡 𝑇 +∞ 𝑛=1 (2.35) in questo modo possiamo definire la variazione sulla traiettoria con i coefficienti di Fourier 𝑎𝑛 ed esprimere l’integrale all’esponente dell’Eq. (2.34) sostituendo ad 𝑦 l’Eq. (2.35), che quindi diventa
𝑚 2∫ [∑ ∑ 𝑛𝜋 𝑇 𝑚𝜋 𝑇 𝑎𝑛𝑎𝑚cos 𝑛𝜋 𝑇 cos 𝑚𝜋 𝑇 − 𝜔 2 ∞ 𝑚=1 𝑇 2∑ 𝑎𝑛 2 ∞ 𝑛=1 ∞ 𝑛=1 ] 𝑑𝑡 𝑇 0 (2.36) =𝑚 2 𝑇 2∑ [( 𝑛𝜋 𝑇) 2 𝑎𝑛2− 𝜔2𝑎𝑛2] ∞ 𝑛=1
Possiamo ora sostituire questo risultato nell’Eq. (2.34) per ottenere il risultato cercato, con un’accortezza: dobbiamo operare un cambio di variabile da 𝑡 ad 𝑎𝑛 e quindi dobbiamo associare ad
ogni 𝑎𝑛 una jacobiana 𝐽, la quale in questo caso è una costante adimensionale il cui valore non ci
interessa, dato che nel corso dell’integrazione sarà incorporata insieme alle altre costanti. Per computare la sommatoria all’infinito presente nell’Eq. (2.36) poniamoci in un caso analogo a quello riportato nel paragrafo 2.3.1 per la particella libera. Stiamo considerando quindi una successione nel tempo di 𝑁 eventi, che si susseguono ogni intervallo di tempo 𝜖; dopo aver calcolare l’equazione per 𝐹(𝑇) procederemo poi a fare il limite per 𝑁 → +∞, in modo da riottenere il risultato corretto. Di conseguenza l’Eq. (2.34) assume la forma
𝐹(𝑇) = 𝐽1 𝐴 ∫ … ∫ 𝑒𝑥𝑝 { 𝑖𝑚 2ℏ 𝑇 2∑ [( 𝑛𝜋 𝑇) 2 𝑎𝑛2− 𝜔2𝑎𝑛2] 𝑁 𝑛=1 }𝑑𝑎1 𝐴 … 𝑑𝑎𝑁 𝐴 +∞ −∞ +∞ −∞ (2.37) dove 𝐴 è un fattore di normalizzazione. Per analogia con l’integrale di percorso della particella libera sappiamo che possiamo trattare ogni integrale separatamente e poi moltiplicare tra loro i singoli risultati, inoltre sappiamo che gli integrali su ogni 𝑎𝑛, che sono tutti gaussiani, hanno soluzioni che possono essere scritte nella forma
𝑐 (𝑛
2𝜋2
𝑇2 − 𝜔2) −1/2
(2.38) dove 𝑐 è una costante che otteniamo dall’integrazione, il cui valore possiamo non computare per il momento, otteniamo che l’Eq. (2.34) diventa
𝐹(𝑇) = 𝑐 ∏ (𝑛 2𝜋2 𝑇2 − 𝜔 2) −1/2 𝑁 𝑛=1 (2.39) = 𝑐 ∏ (𝑛 2𝜋2 𝑇2 ) −1/2 ∏ (1 −𝜔 2𝑇2 𝑛2𝜋2) −1/2 𝑁 𝑛=1 𝑁 𝑛=1
dove in 𝑐 abbiamo accorpato tutte le costanti, compresa la jacobiana 𝐽. Effettuiamo ora il limite per 𝑁 → +∞ e ricaviamo così che il primo termine al prodotto dell’Eq. (2.39) ci fornisce un termine costante che possiamo inglobare in 𝑐, mentre il secondo termine può essere calcolato utilizzando il prodotto infinito notevole di Eulero
21 lim 𝑁→+∞𝑥 ∏ (1 − 𝑥2 𝑛2𝜋2) = sin 𝑥 𝑁 𝑛=1 (2.40) Infatti se poniamo 𝑥 = 𝜔𝑇 ricaviamo che
lim 𝑁→+∞∏ (1 − 𝜔2𝑇2 𝑛2𝜋2) = sin 𝜔𝑇 𝜔𝑇 𝑁 𝑛=1 (2.41) Di conseguenza l’Eq. (2.39) può essere scritta nella forma
𝐹(𝑇) = 𝑐 (sin 𝜔𝑇 𝜔𝑇 )
−1/2
(2.42) Ora non ci rimane che calcolare il valore di 𝑐, e dato che per 𝜔 = 0 ci riduciamo al caso della particella libera sappiamo che possiamo utilizzare il risultato ottenuto nel paragrafo 2.3.1 per evitare ulteriori calcoli. Infatti per 𝜔 = 0 l’Eq. (2.42) assume il valore 𝑐 e dato che possiamo identificare il fattore moltiplicativo nell’Eq. (2.25) con 𝐹(𝑇) otteniamo che
𝑐 = ( 𝑚 2𝜋𝑖ℏ𝑇)
1/2
(2.43) e che quindi, sostituendo l’Eq. (2.42) nell’Eq. (2.41),
𝐹(𝑇) = ( 𝑚𝜔 2𝜋𝑖ℏ sin 𝜔𝑇)
1/2
(2.44) che ci fornisce il fattore moltiplicativo che stavamo cercando.
Quindi sostituiamo l’Eq. (2.33) e l’Eq. (2.44) nell’Eq. (2.32) e ricaviamo l’espressione finale per il Kernel di un oscillatore armonico unidimensionale.
𝐾(𝑏, 𝑎) = ( 𝑚𝜔 2 πiℏsin 𝜔𝑇) 1/2 𝑒𝑥𝑝 { 𝑖𝑚𝜔 2ℏ sin 𝜔𝑇[(𝑥𝑏 2+ 𝑥 𝑎2) cos 𝜔𝑇 − 2𝑥𝑏𝑥𝑎]} (2.45)
dove 𝑇 = 𝑡𝑏− 𝑡𝑎 che in generale non corrisponde al periodo dell’oscillatore. Notiamo in particolare
che Kernel dipende non solo dagli estremi della traiettoria, ma anche dal tempo che la particella impiega a percorrerla. Alcuni valori di 𝑇 sono in particolar modo significativi: consideriamo il caso in cui 𝑇 corrisponda al periodo dell’oscillatore 𝑇𝑃. In questo caso non possiamo definire il valore di
𝐾(𝑏, 𝑎) dato che sin 𝜔𝑇 al denominatore sarebbe nullo. Fisicamente possiamo spiegare questa limitazione con le seguente considerazione: se 𝑇 = 𝑇𝑃 allora 𝑥𝑏= 𝑥𝑎. Il problema nasce dalle ipotesi
iniziali, nelle quali abbiamo posto che 𝑥𝑏 e 𝑥𝑎 sono punti fissi, con la conseguenza che non c’è
indeterminazione sulla loro posizione, e unito al fatto che le funzioni seno e coseno sono periodiche otteniamo che 𝐾(𝑏, 𝑎) non è in grado di distinguere se 𝑇 corrisponde a un periodo o a un suo multiplo intero o semintero. L’intervallo di tempo 𝑇 = 𝑡𝑏− 𝑡𝑎 deve perciò essere necessariamente diverso
dal periodo o dal semi-periodo, altrimenti il 𝐾(𝑏, 𝑎) così espresso non riuscirebbe a determinare se la particella abbia compiuto un giro, due, tre o nessuno: 𝐾(𝑏, 𝑎) non distingue per eventi di durata uguale a 𝑇𝑃 o 𝑇𝑃/2 se la particella abbia effettivamente compiuto un moto o sia rimasta ferma. In
particolare otteniamo anche che 𝐾(𝑏, 𝑎) fornisce lo stesso valore sia per un dato tempo 𝑡 sia per un tempo 𝑇′= 𝑛𝑇𝑃+ 𝑡, con 𝑡 < 𝑇𝑃/2 e con 𝑛 intero o semintero. L’unica differenza tra il caso in cui
𝑛 = 0, 1, 2, … o 𝑛 = 1/2, 3/2, … è che se nel primo caso 𝑥𝑏 >𝑥𝑎 allora nel secondo 𝑥𝑏< 𝑥𝑎.
Questa caratteristica è quella che attendavamo, infatti ci mostra che non solo il moto dell’oscillatore è periodico, ma anche il Kernel è periodico dello stesso periodo 𝑇𝑃.
22
Di conseguenza è lecito considerare 𝑡 e non 𝑇′ nel calcolo di 𝐾(𝑏, 𝑎); così facendo evitiamo il problema dei punti fissi 𝑎 e 𝑏, che se fossero dei punti reiteranti nel nostro evento saremmo in un caso analogo a quello di eventi successivi nel tempo, per le motivazioni espresse nel paragrafo 2.2.1, e dovremmo quindi trattare il Kernel totale dell’evento come il Kernel di 𝑛 eventi identici, dove 𝑛 è il numero di periodi compiuti, e di un evento che coinvolge solo una parte del periodo. Con la periodicità di 𝐾(𝑏, 𝑎) possiamo quindi considerare semplicemente le sezioni di traiettoria in cui 0 < 𝑡 < 𝑇𝑃/2, senza curarci quanti giri la particella potrebbe già aver compiuto.
2.3.3 Effetto Aharonov-Bohm
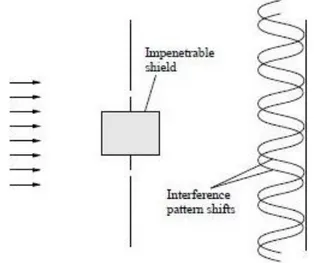
In questo paragrafo illustreremo un esempio su come si possano utilizzare gli Integrali di Percorso per spiegare effetti puramente quantistici; in particolare tratteremo l’effetto di Aharonov-Bohm, il quale si collega con l’esperimento delle fenditure descritto nel Capitolo 1.
Quest’effetto consiste nell’influenza del potenziale elettromagnetico sul moto di una particella, anche se questa è in una regione spaziale completamente schermata da campi elettrici e magnetici. Al fine di dimostrare Aharonov-Bohm consideriamo un esperimento concettuale simile a quello di Young per le due fenditure. Abbiamo in questo caso una sorgente 𝑆 di particelle cariche, una parete opaca 𝐶 con due fenditure 𝐹1 e 𝐹2 equidistanti dalla normale a 𝐶 passante per 𝑆 e uno schermo 𝐵 a
valle che registra l’arrivo delle particelle, poniamo elettroni. Assumiamo poi che tra 𝐹1 e 𝐹2 sia
presente un flusso magnetico arbitrario dal quale gli elettroni sono perfettamente schermati. Ciò che si verifica è che il profilo di interferenza registrato da 𝐵 non è invariante rispetto al flusso magnetico tra le due fenditure, nonostante il fatto che gli elettroni non subiscano alcuna forza da suddetto flusso, siccome ne sono perfettamente schermati.
Fig. 2.1: Effetto di Aharonov-Bohm; il flusso magnetico, da cui gli elettroni sono schermati, si trova all’interno del rettangolo al centro.
Per spiegare quest’effetto, di cui riportiamo una schematizzazione nella Fig. 2.1, possiamo utilizzare gli Integrali di Percorso. Consideriamo allora due traiettorie 𝑥1(𝑡) e 𝑥2(𝑡) passanti rispettivamente
per 𝐹1 e per 𝐹2 e che terminano nello stesso punto sullo schermo 𝐵; in particolare ad entrambe sono
associate le Azioni 𝑆[𝑥1(𝑡)] e 𝑆[𝑥2(𝑡)] e dunque delle ampiezze di probabilità 𝜙[𝑥1(𝑡)] e 𝜙[𝑥2(𝑡)],
23
meno un flusso magnetico tra le fenditure, tra le fasi dell’interferenza di una coppia qualsiasi di 𝜙[𝑥1(𝑡)] e 𝜙[𝑥2(𝑡)]: identificando questo termine per una coppia qualsiasi di ampiezze possiamo generalizzarlo a tutte, dimostrando la variazione sul profilo di interferenza dell’effetto Aharonov-Bohm.
Sommiamo quindi 𝜙[𝑥1(𝑡)] e 𝜙[𝑥2(𝑡)] e raccogliamo 𝜙[𝑥1(𝑡)], in questo modo:
𝑒ℏ𝑖𝑆[𝑥1(𝑡)]+ 𝑒ℏ𝑖𝑆[𝑥2(𝑡)] = 𝑒ℏ𝑖𝑆[𝑥1(𝑡)](1 + 𝑒𝑖𝛿0) (2.46)
dove 𝛿0 rappresenta la fase associata all’interferenza tra le due traiettorie ed obbedisce alla relazione
𝛿0 = 𝑆[𝑥2(𝑡)] − 𝑆[𝑥1(𝑡)]
ℏ (2.47)
Di conseguenza a seconda del valore di 𝛿0 avremo interferenze costruttive o distruttive, come ci attendiamo dall’esperimento di Young. Ora quindi non ci resta che calcolare 𝛿0 nel nostro caso, che
chiamiamo 𝛿, e in particolare dato che per ipotesi tra le fenditure è presente un flusso magnetico 𝐁 = ∇ × 𝐀, dove 𝐀 è il potenziale vettore, possiamo scrivere la lagrangiana del sistema come
𝐿(𝒙̇, 𝒙) = 𝐿0(𝒙̇, 𝒙) −𝑒
𝑐𝒙̇ ∙ 𝐀(𝒙) (2.48) dove 𝐿0(𝒙̇, 𝒙) indica la lagrangiana associata all’elettrone nel caso in cui non ci sia campo magnetico
tra le fenditure e che quindi, se integrata nel tempo, ci fornisce 𝑆[𝑥1(𝑡)] e 𝑆[𝑥2(𝑡)]. Per questo motivo, ai nostri fini, nel calcolo di 𝛿 possiamo considerare solo il secondo termine nell’Eq. (2.48): infatti, sfruttando la definizione dell’Azione data dall’Eq. (2.2) e inserendo le nuove 𝑆[𝑥1(𝑡)] e
𝑆[𝑥2(𝑡)] nell’Eq. (2.46), ricaviamo che 𝛿 = 𝛿0− ∫ 𝑒
ℏ𝑐𝑑𝒙̇ ∙ 𝐀(𝒙)𝑥2(𝑡)− ∫ 𝑒
ℏ𝑐𝑑𝒙̇ ∙ 𝐀(𝒙)𝑥1(𝑡) (2.49) Otteniamo perciò che la differenza tra le fasi dell’interferenza, nel caso in cui 𝐁 sia presente o meno, è data da 𝛿 − 𝛿0 = − 𝑒 ℏ𝑐(∫ 𝑑𝒙̇ ∙ 𝐀(𝒙)𝑥 2(𝑡) − ∫ 𝑑𝒙̇ ∙ 𝐀(𝒙) 𝑥1(𝑡) ) (2.50) Se quindi il termine a destra dell’Eq. (2.50) varia al variare di 𝐁 abbiamo trovato una spiegazione all’effetto di Aharonov-Bohm. Per esprimerlo ci basta riconoscere che è un integrale di contorno e quindi denominarlo con
∫ 𝑑𝒙̇ ∙ 𝐀(𝒙)
𝑥2(𝑡)
− ∫ 𝑑𝒙̇ ∙ 𝐀(𝒙)
𝑥1(𝑡)
= ∮ 𝑑𝒙̇ ∙ 𝐀(𝒙) = Φ (2.51) che in generale può essere non nullo e quindi causare la variazione nel profilo di interferenza. Per terminare la trattazione dell’argomento non ci resta quindi che generalizzare questo risultato a tutte le ampiezze possibili. Consideriamo quindi i Kernel 𝐾(𝑏, 1) e 𝐾(𝑏, 2), i quali rappresentano i contributi di tutte le traiettorie passanti rispettivamente per la prima e la seconda fenditura, e che assumono la forma