Le Sospensioni
A.1 Definizione elastocinematica
Lo scopo fondamentale di una sospensione è di rendere possibile il movimento relativo, principalmente in direzione verticale, fra l'asse di ciascuna ruota e ciò che viene considerato come la massa sospesa, mediante opportuni cinematismi.
Per contrastare “dolcemente” il movimento relativo e per ripristinare la configurazione originale, una volta che le cause perturbative siano cessate, è necessario dotare ogni sospensione di elementi di reazione elastici, ovvero di molle. L'introduzione di tale elasticità comporta la nascita inevitabile di oscillazioni, per il cui rapido smorzamento, è necessario utilizzare appositi elementi, detti ammortizzatori, che consentano anche di limitare l'ampiezza di oscillazione in condizioni di risonanza.
Riassumendo, una sospensione è costituita fondamentalmente da tre elementi: un cinematismo, una molla e un ammortizzatore [13].
Con il termine molla è indicato comunemente un elemento che reagisce all'azione cui è soggetto deformandosi in maniera crescente al crescere dell'azione
stessa, e si riporta nella condizione iniziale al cessare dell'azione deformante. La forza generata dalla molla è uguale e contraria alla forza F che ha prodotto la deformazione (Fig. A.1).
Fig. A.1 – Rappresentazione schematica di una molla comune in condizione di riposo e caricata.
Le molle generano una forza proporzionale alla variazione della loro lunghezza l , la relazione fra forza e deformazione sarà quindi:
F =k⋅ l (A.1)
Dove la costante elastica k è la rigidezza della molla [N/m].
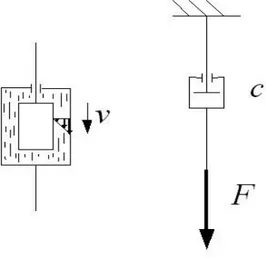
Fig. A.2 – Schematizzazione di smorzatore viscoso con due cilindri concentrici e sua rappresentazione schematica.
L'ammortizzatore è il componente che funge da smorzatore, cioè è un elemento che reagisce alle azioni esterne con forze legate alla velocità lineare v. In genere il legame fra queste grandezze è di tipo lineare:
F =c⋅v (A.2)
dove con c [ N⋅s/ m] è indicata la costante di smorzamento viscoso. L'ammortizzatore è comunemente schematizzato con un accoppiamento fra due cilindri con una piccola intercapedine riempita da fluido che può considerarsi viscoso Newtoniano in moto laminare di tipo Couette, cioè con derivata della velocità, nella direzione del moto, costante, per cui la forza risultante sarà proporzionale alla velocità (Fig. A.2) [8].
A.2 Vibrazioni libere
Si consideri il sistema semplice a un grado di libertà di Fig A.3, in cui la massa M è connessa al telaio mediante una molla di costante k , uno smorzatore viscoso di costante c ed è in grado di muoversi soltanto in una direzione.
Fig. A.3 – Sistema oscillante a un grado di libertà.
Si supponga che il piano rappresentato sia verticale, che la situazione illustrata corrisponda alla posizione di riposo e inoltre che la forza peso sia nulla.
Scegliendo come riferimento l'asse x di figura, la massa è soggetta a un certo numero di forze le cui componenti lungo l'asse x sono:
• −k⋅x , forza elastica con verso opposto a x ;
• −c⋅dx /dt , forza di smorzamento viscoso, con verso opposto a
dx / dt ;
• −M⋅d2x /dt2 , forza d'inerzia con verso opposto a d2x / dt2 .
L'equazione di d'Alembert sarà:
−k⋅x−c⋅dx dt=M⋅
d2x
dt2 (A.3)
con semplici passaggi l'equazione (A.3) può essere riscritta come:
M⋅d 2 x dt2 c⋅ dx dt k⋅x=0 (A.4)
Questa è la forma più comune dell'equazione differenziale del moto di una massa oscillante, un'equazione differenziale del secondo ordine, lineare, omogenea a coefficienti costanti.
Come noto l'equazione (A.4) ha una soluzione del tipo:
x t =ez⋅t (A.5)
che, sostituita nella (A.4) porta adover risolvere l'equazione caratteristica:
M⋅z2c⋅zk =0 (A.6) da cui: z1,2= −c 2⋅M±
c2−4⋅M⋅k 2⋅M (A.7)Se c2
≠4⋅M⋅k si hanno due soluzioni distinte e l'integrale dell'equazione (A.4) è del tipo:
x t =1⋅ez1⋅t2⋅ez2⋅t (A.8)
con 1 e 2 costanti arbitrarie dipendenti dalle condizioni iniziali del sistema. Se si indica con n la pulsazione naturale del sistema, espressa come:
n=
k M (A.9) e si pone: ⋅n= c 2⋅M (A.10) ovvero: = c ccr (A.11) con: ccr=2⋅
M⋅k (A.12)dove con si indica il fattore di smorzamento, con ccr lo smorzamento critico, allora l'espressione (A.7) può essere riscritta:
z1,2=−⋅n±n⋅
2−1 (A.13)Quindi l'equazione (A.4) si riscrive come: d2x dt2 2⋅⋅n⋅ dx dt n 2 ⋅x=0 (A.14)
quello critico, ovvero se 1 , 1 o =1 , possono presentarsi tre casi [8].
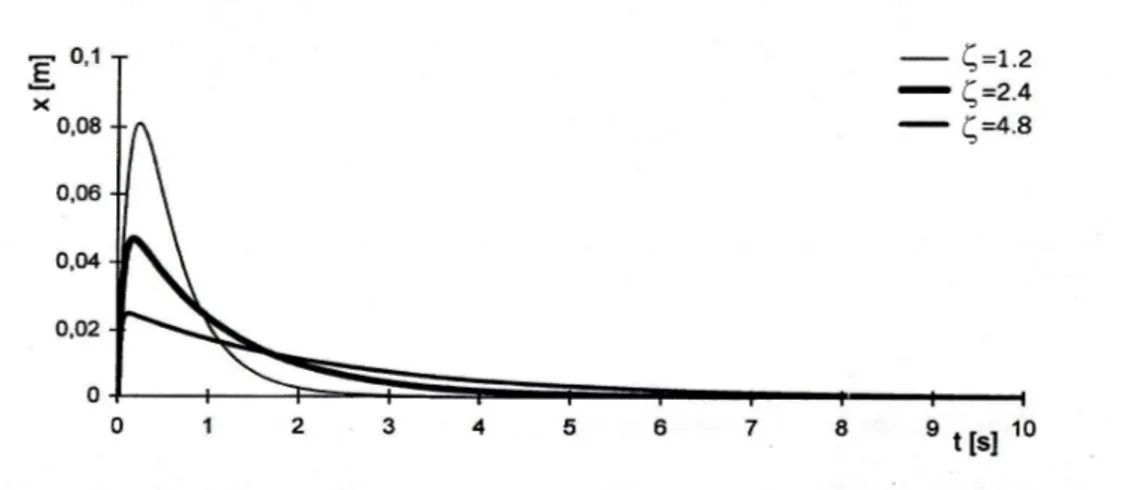
A.2.1 Oscillazioni con smorzamento superiore a quello critico
Se 1 ,cioè se c24⋅M⋅k , la (A.8), sfruttando le espressioni per le radici nella forma (A.13), può essere riscritta come:
x t =e−⋅n⋅t⋅A⋅e
2
−1⋅n⋅tB⋅e−
2
−1⋅n⋅t (A.15)
Le costanti arbitrarie A e B sono da determinarsi in base alle condizioni iniziali del sistema.
Fig. A.4 – Andamento dell'oscillazione aperiodica smorzata per diversi fattori di smorzamento.
Il moto è dunque aperiodico smorzato, di cui in Fig. A.4 è riportato il tipico andamento al variare dello smorzamento [8].
A.2.2 Oscillazioni con smorzamento inferiore a quello critico
Se 1 , cioè se c2
4⋅M⋅k , può essere definita una pulsazione dell'oscillazione smorzata mediante la relazione:
=n⋅
1−Fig. A.5 – Andamento dell'oscillazione e relative curve di estinzione del moto periodico smorzato.
Se si utilizzano le espressioni (A.13), (A.16) e introducendo l'unità immaginaria i , è possibile riscrivere la (A.8) nella forma:
x t =e−⋅n⋅t⋅A⋅ei⋅⋅t
B⋅e−i⋅⋅t
(A.17)
o alternativamente nella forma:
x t =e−⋅n⋅t⋅D⋅sin
⋅t (A.18)
Se ne deduce che il moto è periodico smorzato con periodo T pari a:
T=2⋅⋅= 1
f (A.19)
dove con f si è indicata la frequenza di oscillazione. L'andamento tipico di x t è rappresentato in Fig. A.5, cioè di una sinusoide con inviluppo compreso fra due curve di esponenziali di andamento ±D⋅e−⋅n⋅t . Si può notare che la
in assenza di smorzamento, infatti in quest'ultimo caso il moto è puramente sinusoidale con pulsazione n (basta porre =0 ). Come nel caso precedente
D e sono ottenuti a partire dalle condizioni iniziali [8].
A.2.3 Oscillazioni con smorzamento critico
Se =1 , ovvero se c2
=4⋅M⋅k la soluzione generale assume la forma:
x t =e−n⋅t⋅E F⋅t (A.20)
a cui sono associati degli spostamenti con andamenti simili al caso con moto aperiodico smorzato. Al solito E ed F sono fissati dalle condizioni iniziali [8].
A.3 Vibrazioni forzate: moto impresso dalle irregolarità stradali
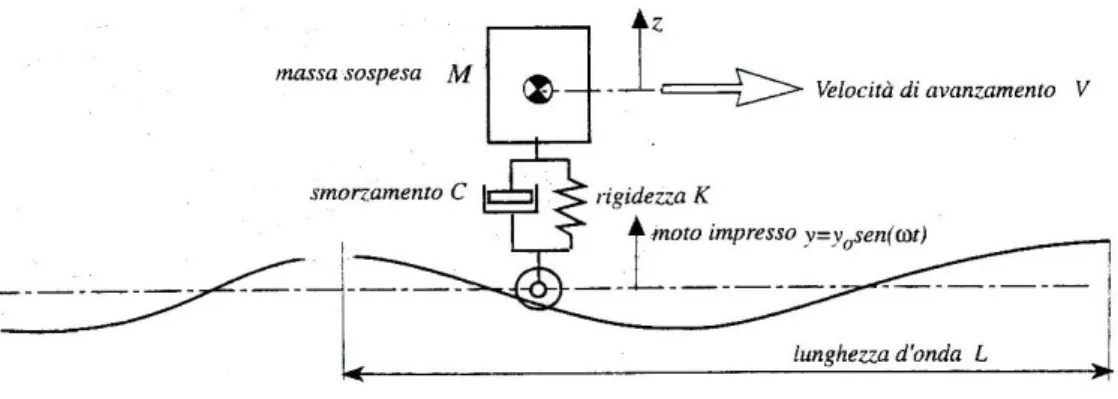
In genere il campo di frequenze considerato nello studio del veicolo nel suo insieme, va da 0,25 Hz a 20 Hz , le eccitazioni a bassissime frequenze, cioè sotto 0,25 Hz , sono causate dalle naturali variazioni di pendenza della strada, che il veicolo deve fedelmente seguire. Gli pneumatici sono realizzati con rigidezza radiale molto maggiore della rigidezza delle sospensioni, per cui per frequenze inferiori ai 3 Hz , il contributo degli pneumatici può essere trascurato, ossia possono essere considerati radialmente rigidi.L'obiettivo della sospensione è quindi quello di rendere ottimale il comportamento del veicolo anche su strada non perfettamente livellata, quindi se si considera un veicolo, schematizzato come una massa M sospesa da una monosospensione, viaggiante a velocità costante v , su un certo profilo stradale, si desidera che il veicolo si muova meno possibile in direzione verticale.
Schematizzando tale situazione come fatto in Fig. A.6, si può considerare la sospensione eccitata dal moto impresso dalle irregolarità stradali. Il punto di contatto della ruota con il profilo stradale sarà in moto armonico, secondo la legge:
y= y0⋅sin i⋅t (A.21)
dove i rappresenta la pulsazione del moto impresso al sistema dale irregolarità del fondo stradale:
i=2⋅ Ti
=2⋅
Li ⋅v (A.22)
Il periodo Ti del moto impresso, è dato dal rapporto fra la lunghezza d'onda Li del profilo stradale e la velocità di avanzamento v.
Si può dimostrare facilmente che in condizioni di regime, il rapporto fra l'ampiezza verticale della massa sospesa e l'ampiezza y0 del moto impresso, risulta: G=X0 Y0 =
12⋅2⋅i n
1−
i n
2
2
2⋅⋅i n
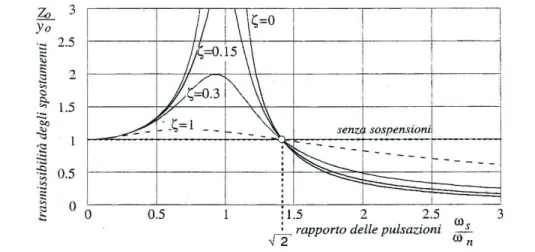
2 (A.23)Il rapporto G prende il nome di trasmissibilità degli spostamenti. In Fig. A.7 sono rappresentate le curve della trasmissibilità G al variare del rapporto di smorzamento .
Fig. A.8 – Trasmissibilità delle accelerazioni al variare del rapporto delle frequenze.
Dal grafico si evince che la trasmissibilità, indipendetemente dallo smorzamento, è sempre unitaria in corrispondenza del valore
2 del rapporto delle frequenze. Il grafico mette in luce che:• per valori del rapporto delle frequenze minori di
2 , l'introduzione( G>1 ). L'adozione delle sospensioni si rivela utile ( G<1 )solo per valori del rapporto delle frequenze maggiore di
2 ;• valori elevati del rapporto di smorzamento attenuano l'aumento di
trasmissibilità, per rapporti delle frequenze minori di
2 , ma peggiorano la risposta alle frequenze maggiori.In Fig. A.8 è riportato l'andamento della trasmissibilità dell'accelerazione verticale, al variare del rapporto delle frequenze, per diversi valori del rapporto di smorzamento della sospensione. Come si evince da Fig A.8, tutte le curve assumono sempre lo stesso valore, uguale a 2 , in corrispondenza del rapporto delle frequenze pari a
2 , pur presentando pendenze differenti, inoltre si nota che si ha pendenza nulla per =
2/4=0,354 .La curva caratterizzata da tale valore di garantisce le minime accelerazioni nell'intorno del punto i/n=
2 perciò essa rappresenta il valore ottimale nell'intorno del punto considerato.Dal grafico di Fig. A.8 si può concludere che la sospensione si comporta come un filtro che taglia le alte frequenze amplifica quelle che si trovano in una stretta banda attorno alla condizione di risonanza, cioè per i/n=1 , inoltre una riduzione notevole di trasmissibilità può essere ottenuta diminuendo la rigidezza delle sospensioni, ossia adottando delle molle più soffici. Occorre osservare che nel caso del veicolo, molle eccessivamente cedevoli, possono compromettere gravemente l'assetto del veicolo soprattutto nelle fasi di accelerazione rapida e brusca frenata [9], [13].
A.4 Classificazione delle sospensioni
Si analizzano brevemente gli schemi cinematici delle sospensioni anteriori e posteriori attualmente più diffusi sui motoveicoli.
A.4.1 Sospensioni anteriori
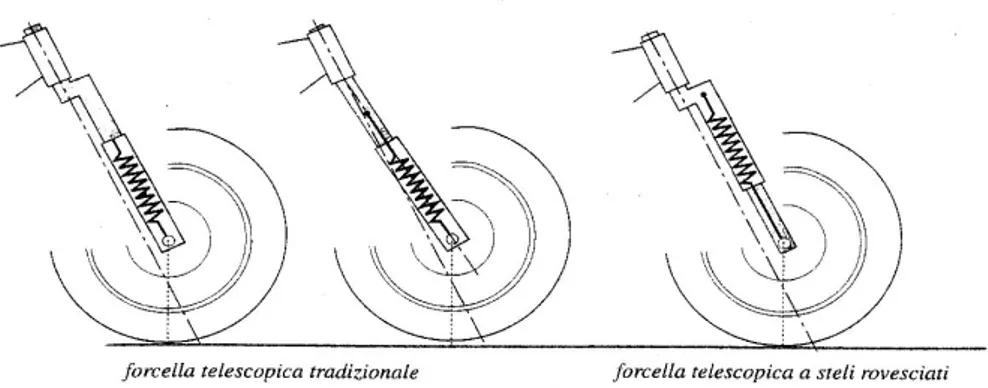
La sospensione anteriore maggiormente diffusa è la forcella telescopica: si costituisce di due steli che scorrono all'interno di due foderi, in modo da realizzare una coppia prismatica che collega la ruota anteriore al telaio del veicolo.
Fig. A.9 – Sospensione anteriore a forcella telescopica classica e rovesciata.
La soluzione costruttiva con i due steli fissati al canotto di sterzo è detta “a steli tradizionali”, è attualmente lo schema costruttivo più diffuso per i motocicli da turismo (Fig. A.9).
La soluzione con i due foderi fissati al canotto di sterzo e i due steli nella parte inferiore è detta “a steli rovesciati” ed è la più comune sui veicoli sportivi, soprattutto per la maggiore rigidezza torsionale e flessionale.
Fig. A.10 – Sospensione anteriore a braccio oscillante spinto e tirato.
cinematico, le seguenti sospensioni:
• a braccio oscillante spinto; • a braccio oscillante tirato; • a quadrilatero.
Nella sospensione anteriore a braccio oscillante il braccio può essere “spinto”, è il caso di forcella di tipo Earles, oppure “tirato”, come accade sulla Vespa Piaggio (Fig. A.10).
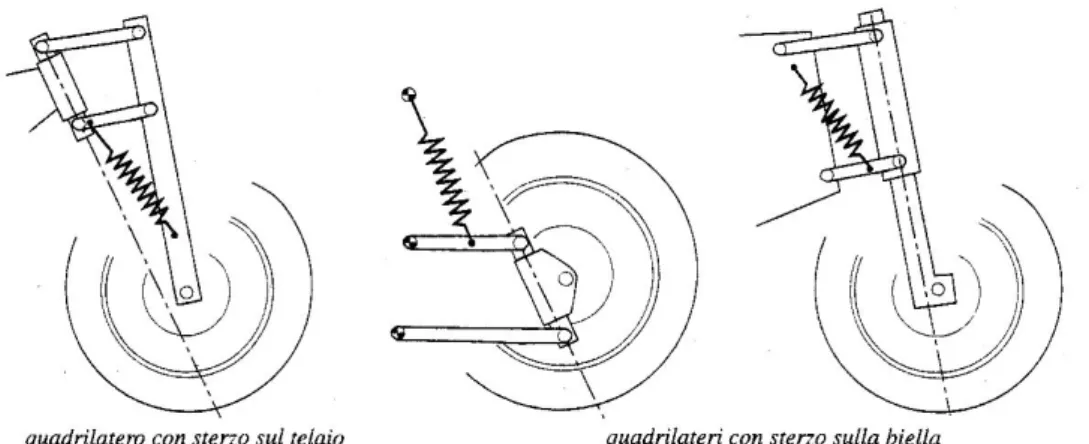
Fig. A.11 – Sospensioni anteriori a quadrilatero.
Anche il meccanismo a quadrilatero può essere utilizzato per realizzare una sospensione anteriore, in tal caso è possibile che la sospensione presenti un asse di sterzo vincolato al telaio o alla biella,come mostrato in Fig. A.11.
Una variante della sospensione anteriore a quadrilatero si ottiene sostituendo una coppia rotoidale con una coppia prismatica (Fig. A.12). L'inconveniente di tale schema è nella rotazione del manubrio attorno alla coppia rotoidale superiore fissata al telaio per effetto del moto verticale della ruota. L'inconveniente si riduce drasticamente spostando la coppia rotoidale fissata al telaio, in corrispondenza dell'asse di sterzo, soluzione che viene adottata nel sistema “Telelever” della BMW [9].
A.4.2 Sospensioni posteriori
La sospensione posteriore classica è composta da un forcellone costituito da due bracci oscillanti, con due gruppi molla-ammortizzatore, posti su entrambi i lati, inclinati rispetto al forcellone di un determinato angolo (Fig. A.13).
Fig. A.13 – Sospensione posteriore a braccio oscillante classico.
Una variante della sospensione a forcellone è il sistema denominato “cantilever”, caratterizzato da un solo gruppo molla ammortizzatore. Tale sospensione non consente però la realizzazione di curve di progressività elevate, inoltre il posizionamento del gruppo molla-ammortizzatore sopra o dietro il motore può comportare problemi di dissipazione del calore prodotto dall'ammortizzatore stesso. È possibile pensare di introdurre un meccanismo nella sospensione posteriore per migliorare il sistema “cantilever”. I diversi schemi sono basati generalmente sul quadrilatero e si distinguono solo per il diverso
attacco del gruppo molla-ammortizzatore. Se questo è inserito tra il telaio e il bilanciere si tratta dello schema Unitrak della Kawasaki, se fra la biella e il telaio si tratta del sistema Pro-Link Honda, mentre se è posto fra il bilanciere e il forcellone, è il caso dello schema Full Floater Suzuki, come illustrato in Fig. A.14 [9].