Breve introduzione Alla modulazione OFDM

Breve introduzione

Alla modulazione

OFDM

Introduzione

In questo capitolo viene introdotta la modulazione OFDM (Orthogonal Frequency Division Multiplexing), la sua implementazione attraverso la FFT (Fast Fourier Transform) e gli aspetti generali della modulazione. Viene inoltre definito e calcolato il PAR (Peak to average ratio) per un segnale OFDM.

1.1 – La modulazione OFDM

La modulazione OFDM (Orthogonal Frequency Division Multiplexing) cerca di risolvere il problema dovuto ai canali selettivi in frequenza, suddividendo la trasmissione di un unico flusso dati ad alta velocità di segnalazione 1/T, e quindi a larga banda, in una molteplicità di sottoflussi paralleli. Indicando con N il numero di sottoflussi, la velocità di segnalazione su ognuna delle N sottoportani

diventa s T N T 1 / 1

= . Cosi facendo si avrà, su ogni sottoflusso, un segnale la cui banda sarà dell’ordine di 1/Ts e quindi N volte più piccola del caso di un unico

può fare in modo che il segnale su ciascuna sottoportante abbia una banda minore della banda di coerenza del canale. In questo modo il segnale su ciascuna sottoportante si propagherà attraverso un canale sostanzialmente piatto e quindi non distorcente. L’unico effetto dovuto al canale sulla generica sottoportante è quello di introdurre uno sfasamento e un’attenuazione che possono essere recuperati in ricezione.

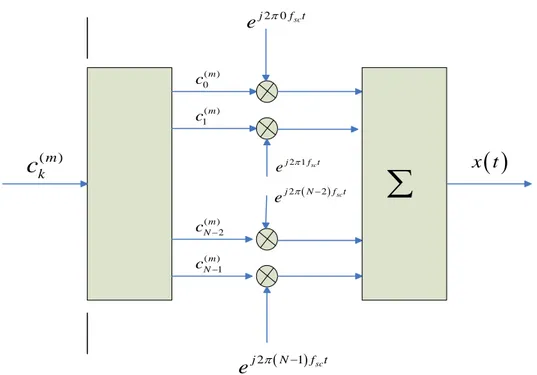
Bisogna, adesso, capire come effettuare efficacemente la modulazione di questi sottoflussi paralleli e quale deve essere la spaziatura tra le varie sottoportanti che indichiamo momentaneamente con fsc. Lo schema di massima del modulatore multiportante è il seguente [1]: (m) k

c

( ) 0 m c ( ) 1 m c ( ) 1 m N c ₋ ( ) 2 m N c ₋ 2 0 sc j f t e π 2 1sc j f t e π ( ) 2 1 sc j N f t e π − ( ) 2 2 sc j N f t e π −

∑

( )

x t

Figura 1.1: generazione del segnale OFDM

I simboli ( )m k

c appartengo all’alfabeto di una modulazione lineare arbitraria ( M-PSK, MQAM) e sono caratterizzati da una velocità di informazione pari a 1/T. Il flusso di tali simboli sorgenti viene parallelizzato in N sottocanali su ciascuno dei quali l’ intervallo di simbolo diventa T_s =NT che viene chiamato intervallo di

simbolo OFDM. Il convertitore serie-parallelo induce una sorta di

partizionamento a blocchi dei simboli d’ingresso, con dimensione del blocco pari a N simboli di sorgente ovvero di un simbolo OFDM. Indico con k l’indice di sottoportante, che va da 0 a N-1, e con m l’indice temporale del generico simbolo OFDM . L’espressione del segnale modulato è:

∑ ∑

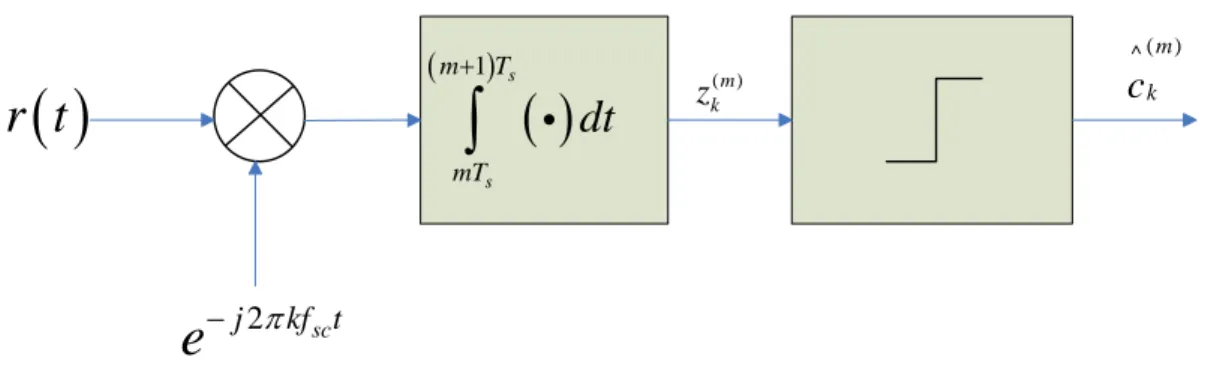
+∞ −∞ = − = − = m N k t f j s m k sc e mT t p c t x 1 0 2 ) ( ) ( ) ( π (1.1)

dove p(t) è un impulso rettangolare d’ampiezza unitaria non nullo per 0≤t ≤Ts e dove i simboli di sorgente sono normalizzati a potenza unitaria (c_k(m) 2 =1). Consideriamo adesso il k-esimo sottocanale e vediamo come deve essere fatta la demodulazione del corrispondente segnale. Il demodulatore ottimo in regime AWGN per il canale kè il seguente:

( )

( 1) _s s m T mT

dt

+

∫

i

2 _sc j kf t

e

− π

( )

r t

( ) ^ m k c ( )m k z

Figura 1.2: demodulatore segnale OFDM

Esso prevede la conversione in banda base del segnale, il filtraggio adattato, campionamento e decisione a soglia. Indicando con r(t) il segnale ricevuto, la variabile di decisione sul simbolo della k-esima sottoportante è, per l’intervallo di segnalazione con m=0 e trascurando l’effetto del rumore:

∫

− = s sc T t kf j s k r t e dt T z 0 2 ) 0 ( ) ( 1 π (1.2)

La presenza degli altri sottoflussi introduce una interferenza sulla decisione. Calcoliamo l’effetto della presenza del sottocanale i-esimo con i≠k sulla variabile di decisione del ricevitore ottimo per il k-esimo canale considerando

m=0 e trascurando l’effetto del rumore :

∫

= ₋ − = s sc − sc S T sc T f k i j i t kf j i k i f k i j e c dt e c I 0 ) ( 2 0 2 ) 0 ( ) 0 ( , ) ( 2 1 π π π (1.3)

Osservando l’espressione al secondo membro si può notare che l’interferenza (0) ,k

i

I

si annulla quando f_scT_s =q, con q intero, cioè quando le portanti sono ortogonali. E’ conveniente scegliere il valore di q più piccolo in modo da tenere le sottoportanti più vicine possibile e, quindi, limitare la banda del segnale modulato. Si dovrà quindi scegliere:

NT T f s sc 1 1 = = (1.4)

In queste condizioni la modulazione prende il nome di OFDM, ha la minima occupazione spettrale e i dati sui vari sottocanali possono essere recuperati senza interferenza con una batteria di ricevitori come quello in Figura 1.2. Per ottenere il flusso dati originario sarà necessario , dopo tale operazione, riformattare il flusso da parallelo a seriale mediante un convertitore P/S.

Per capire quale sia l’occupazione spettrale del segnale OFDM, consideriamo i simboli (m)

k

c statisticamente indipendenti sia su diversi intervalli di simbolo OFDM sia su ciascuna sottoportante. Questo ci permette di calcolare lo spettro

del segnale come somma degli spettri dei segnali che modulano le diverse sottoportanti.

La densità spettrale di potenza di un processo casuale è per definizione:

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ = ∞ → ∞ → AV T T T AV T T x T f X f X E T f X E f S AV AV AV AV AV ) ( ) ( lim ) ( lim ) ( * 2 (1.5)

Dove TAV è il periodo sul quale viene calcolato lo spettro. Per effettuare il calcolo possiamo considerare TAV che comprende un numero molto elevato di simboli OFDM e quindi basterà considerare m grande. Se i simboli (m)

k

c sono statisticamente indipendenti, a valor medio nullo e varianza

{ }

(m) 2

k

c

E allora la densità spettrale di potenza vale:

∑

− = ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 1 0 , ) ( N k s k x x T k f S f S (1.6)

dove S_x,k(f)è la densità spettrale di potenza del generico sottoflusso sulla

k-esima sottoportante:

{ }

) ( sin ) ( ) ( 2 2 2 ) ( , s s s m k k x P f T c fT T c E f S = = (1.7) e quindi

∑

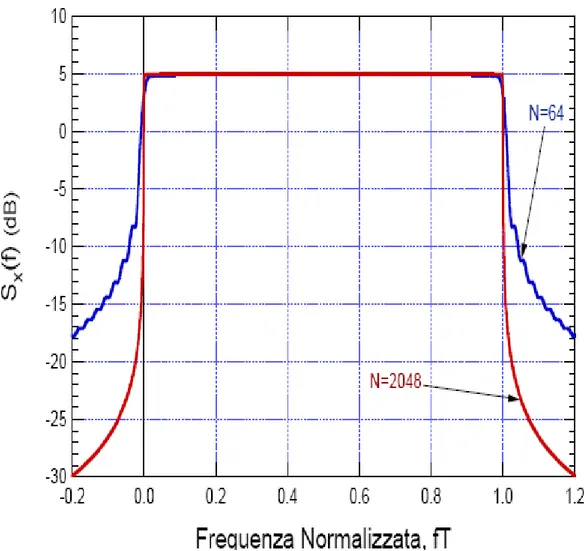
− = ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 1 0 2 sin ) ( N k s s x T k f c T f S (1.8)

Figura 1.3: Spettro del segnale OFDM

In Figura 1.3 è rappresentato lo spettro di un segnale OFDM con 2048 e 64 sottoportanti. Si può notare che la sovrapposizione degli spettri sulle varie sottoportanti da luogo ad uno spettro estremamente piatto in banda e con un rapido decadimento verso lo zero e che queste caratteristiche sono tanto più accentuate quanto più alto è il numero di sottoportanti.

1.2 - Implementazione mediante FFT

Vediamo ora come si può trovare una struttura efficiente di modulatori e demodulatori che realizzino le operazioni finora descritte. Questa esigenza è particolarmente importante in quei sistemi che utilizzano un numero molto elevato di portanti, per esempio nello standard per la diffusione del segnale televisivo digitale terrestre sono previste 8192 sottoportanti. Per derivare la struttura di un modem digitale per OFDM consideriamo il segnale analogico modulato x(t) e campioniamolo con frequenza fc =1/T = N/Ts. In questo modo si ottiene:

[ ]

_{∑ ∑}

+∞ −∞ = − = − = = m N k T N nT j s s m k s s s e mT N nT p c N nT x n x 1 0 1 2 ) ( ) ( ) / ( π (1.9)

Consideriamo il primo simbolo OFDM (m=0). In questo caso si ottiene:

[ ]

_∑

−

_∑

= − = = = 1 0 1 0 / 2 ) 0 ( / 2 ) 0 ( ) ( N k N k N kn j k N kn j s k e c e N nT p c n x π π ,0≤n≤N −1 (1.10)

Si può notare che la sequenza x[n] è pari all’antitrasformata discreta di Fourier della sequenza degli N simboli di sorgenti (0)

1 ) 0 ( 1 ) 0 ( 0 ,c ,...,cN−

c che formano il primo

simbolo OFDM. Grazie a questo possiamo effettuare l’operazione di modulazione in maniera efficiente utilizzando un algoritmo veloce per il calcolo della trasformata inversa di Fourier. In seguito alla IFFT, per ottenere il segnale analogico modulato in banda base, si sovracampiona la sequenza x[n] e la si invia ad un convertitore D/A. Per fare in modo che la sequenza x[n] abbia la stessa potenza a prescindere dal numero di sottoportanti la IFFT viene riformulata nel modo seguente :

[ ]

_∑

− = = 1 0 / 2 ) 0 ( 1 N k N kn j k e c N n x π , 0≤n≤ N−1 (1.11)

Supponiamo che il segnale modulato venga ricevuto senza distorsioni di canale, ma con aggiunta di rumore gaussiano bianco :

) ( ) ( ) (t x t w t r = + (1.12)

Il demodulatore per il k-esimo canale calcola la variabile di decisione:

∫

− = s s T T kt j s k r t e dt T z 0 / 2 ) 0 ( ) ( 1 π (1.13)

Campionando il segnale r(t) alla frequenza fc =1/T =N/Ts e approssimando l’integrale con una somma si ottiene:

[ ]

∑

− = − = 1 0 / 2 ) 0 ( 1 N n N kn j k r ne N z π (1.14)

pari cioè alla trasformata discreta di Fourier della sequenza ricevuta. Anche in questo caso la trasformata viene eseguita con un algoritmo FFT e per normalizzazione viene riformulata nel modo seguente:

[ ]

∑

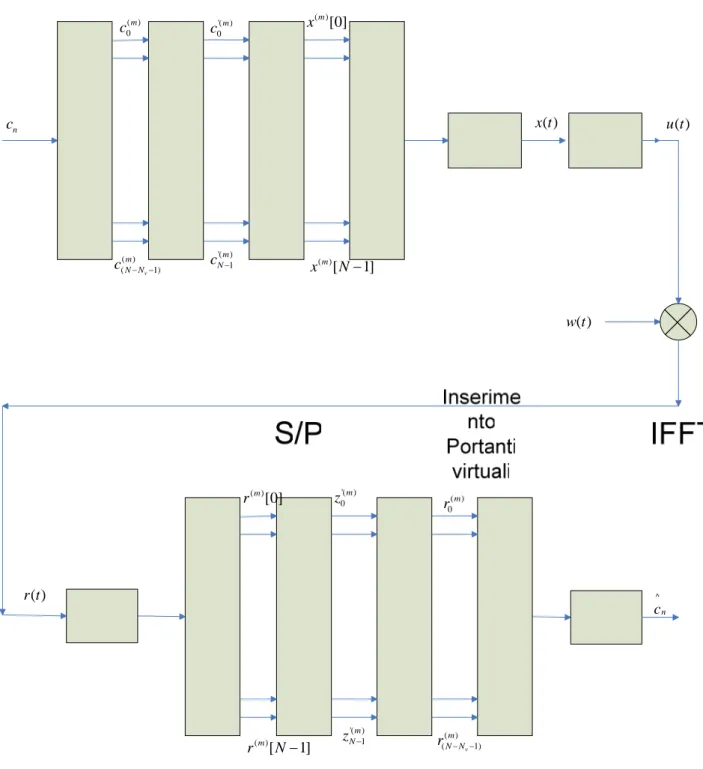
− = − = 1 0 / 2 ) 0 ( 1 N n N kn j k rne N z π , 0≤k≤ N−1 (1.15)

A questo punto è possibile disegnare un primo schema a blocchi del modem OFDM:

n c ( ) 0 m c ( ) ( v 1) m N N c _{− −} '( ) 0 m c '( ) 1 m N c ₋ ( ) [0] m x ( ) [ 1] m x N− ( ) x t ( ) w t ( ) u t ( ) r t ( ) [0] m r ( ) [ 1] m r N− '( ) 0 m z '( ) 1 m N z − ( ) ( v 1) m N N r − − ( ) 0 m r ^ n c

Figura 1.5: Il sistema OFDM

Oltre alle funzioni già descritte compare anche un blocco “Inserimento portanti virtuali”, mentre il numero di simboli di sorgente utili per simbolo OFDM non è pari a N ma a N−Nv . L’inserzione delle cosiddette “portanti virtuali” è una

maniera per controllare precisamente la larghezza di banda del segnale modulato anche con un vincolo, per esigenza di realizzazione, sulla particolare dimensione del calcolatore di (I)FFT utilizzato nel modem (che normalmente elabora blocchi di lunghezze pari a potenze di 2). In sede di formattazione del simbolo infatti, al blocco degli N −Nv simboli utili vengono posposti Nv simboli nulli in modo da arrivare alla lunghezza fissata del blocco di simboli di sorgente che contribuisce a formare il simbolo OFDM tramite IFFT. La presenza di questi simboli nulli in testa e in coda fa sì che le corrispondenti sottoportanti vengano azzerate, cioè diventino “virtuali”. Lo spettro di potenza diventa allora:

∑

− − = ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − =N Nv k s k x x T k f S f S 1 0 , ) ( (1.16)

1.3 - PAR del segnale OFDM

Uno dei problemi relativi ai segnali OFDM è l’elevata variabilità dell’inviluppo complesso che può presentare dei picchi di potenza che si discostano sensibilmente dalla potenza media dell’inviluppo complesso. L’HPA (High Power Amplifier) utilizzato nel sistema di comunicazione ha una caratteristica ingresso-uscita nonlineare a causa della quale “le componenti del segnale” caratterizzate da un’ ampiezza sensibilmente diversa da quella media saranno amplificate in maniera differente e questo risulta in una distorsione del segnale in uscita. Questi picchi di potenza porteranno a lavorare l’HPA vicino al punto di saturazione o addirittura, se superano il range dell’amplificatore, daranno luogo al fenomeno del clipping. Un parametro importante che quantifica in qualche modo la variabilità dell’inviluppo complesso di un segnale è il PAR (peak-to-

average-ratio)che a sua volta è legato ad un altro parametro chiamato crest

factor, CF.

Definisco PAR

{ }

x_τ , dove τ rappresenta l’indice n per un segnale tempo-discreto e il parametro t per un segnale tempo-continuo, la seguente quantità[2,3]:

{ }

_{{ }}

₂ 2 max τ τ τ τ x E x x PAR = (1.17) 2

maxx_τ è la potenza istantanea massima, E

{ }

xτ 2 è la potenza media del segnale

e τ è l’ intervallo di tempo nel quale viene valutato il PAR. Il PAR è strettamente legato ad un’ altro parametro chiamato Crest Factor (CF) definito nel modo seguente:

) ( max τ τ τ x RMS x CF = (1.18)

dove RMS x( )_τ indica il valor quadratico medio di x_τ (Root Mean Square). Un segnale caratterizzato da un CF basso è un segnale che per gran parte del tempo in cui viene osservato assume valori prossimi a _τ

τ x

max . E’ facile rendersi conto che questi due parametri sono legati dalla seguente relazione:

{ }

2

CF x

PAR _τ = (1.19) Per un segnale tempo discreto ,

x

_τ viene sostituito con i campioni _⎢⎣⎡ _⎥⎦⎤

L n x(m)

∑

− = = 1 0 / 2 ) ( ) ( ) ( N k T kt j m k m _{t c e} s x π _(1.20)

Nelle trasmissioni in banda passante il segnale x(t) viene modulato su una portante fc e può essere scritto nel seguente modo:

{

( )

}

( )cos(2 ) ( )sin(2 ) Re

)

(t x t e 2 x t f t x t f t

x_PB = j πfct = _I π _c − _Q π _{c (1.21)}

Nel caso in cui

S c

T N

f >> _{, il massimo del segnale x(t) è lo stesso del segnale}

) (t x_PB : ) ( max ) ( maxx_PB t ≅ x t (1.22)

Per modulazioni MQAM/MPSK vale:

{

2

}

{ }

2

{ }

2 ) ( 2 1 ) ( ) (t E x t E x t x E I = Q = (1.23) e:

{

2

} { }

2 ) ( 2 1 ) (t E x t x E PB = (1.24) quindi:

{

}

_{

_{} { }}

2

{ }

( ) 2 / ) ( ) ( max ) ( ) ( max ) ( ₂ 2 2 2 t x PAR t x E t x t x E t x t x PAR PB PB PB = = = τ τ _(1.25)

dalla quale risulta che il PAR di un segnale a radio frequenza è il doppio di quello relativo al suo inviluppo complesso.

Valutiamo, adesso, il PAR di un segnale OFDM:

[

]

_∑

− = = 1 0 / 2 ) ( ) ( 1 / N k NL kn j m k m e c N L n x π (1.26)

il cui picco di potenza vale:

[ ]

1 2 0 ) ( 2 1 0 / 2 ) ( 2 ) ( max 1 1 / max ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≤ =

∑

∑

− = − = N k m k N k NL kn j m k m n x n L _N c e _N c π (1.27)

L’uguaglianza vale, per esempio per n=0, quando tutti i (m)

k

c hanno la stessa fase e quindi, sommandosi in fase si ottiene il massimo modulo pari proprio alla somma dei moduli dei ck.

Dalla (1.26) utilizzando il teorema di Parseval si ottiene:

{

}

∑

−

{ }

= = 1 0 2 ) ( 2 ) ( 1 ] / [ N k m k m c E N L n x E (1.28)

Per cui il PAR del segnale diventa nel caso peggiore:

[

]

{

}

_{{ }}

_{( )} 2 2 ) ( ) ( max / m k m k m c E c N L n x PAR ≤ (1.29)

dove la quantità al numeratore dipende dal simbolo di informazione effettivamente trasmesso sulla k-esima portante durante l’m-esimo intervallo di

simbolo OFDM, mentre la quantità al denominatore dipende dalla costellazione dei simboli adottata.

Per valutare la funzione distribuzione di probabilità del PAPR supponiamo che i simboli ck(m)siano variabili aleatorie (VA) gaussiane a valor medio nullo,

varianza unitaria e indipendenti. Si consideri l’espressione dei campioni x(m)[n]:

[ ]

_∑

− = = 1 0 / 2 ) ( ) ( 1 N k N kn j m k m e c N n x π (1.30)

essa rappresenta una combinazione lineare di VA gaussiane e quindi anche gli

] [

) (

n

xm sono VA gaussiane . Inoltre il fatto che la trasformazione (1.30) utilizza funzioni ortogonali fa si che gli x(m)[n]siano indipendenti, infatti :

{

}

( )

{

}

( ) 1 1 ] [ ] [ 1 0 / 2 / 2 * ) ( ) ( * 1 0 / 2 ) ( 1 0 / 2 ) ( * ) ( ) ( s r e e c c E N e c e c E N s x r x E N k N ks j N kr j m k m k N k N ks j m k N l N lr j m l m m − = = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ =

∑

∑

∑

− = − − = − = δ π π π π (1.31)

La precedente relazione dimostra che i campioni

x

(m)

[

n

]

sono tra loro incorrelati ed essendo VA gaussiane sono anche indipendenti. Con questa assunzione è possibile calcolare la funzione distribuzione di probabilità CDF (Cumulative Distribution Function) nel modo seguente:

{

}

{

}

_{

_}

_{

_}

_{

_}

{

}

N m m m m m m m m m n x E n x P n x E N x n x E x n x E x P n x PAR P ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ < = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ < − < < = < 2 2 ) ( 2 ) ( 2 2 ) ( 2 ) ( 2 2 ) ( 2 ) ( 2 2 ) ( 2 ) ( 2 ) ( ] [ ] [ ] [ ] 1 [ , ,... ] [ ] 1 [ , ] [ ] 0 [ ] [ γ γ γ γ γ (1.32)

Nel caso di segnale OFDM reale e in banda base la CDF diventa:

[ ]

{

}

{

m

}

(

( )

)

N Q n x PAR P ( ) <γ2 = 1−2 γ (1.33) e quindi, la funzione distribuzione di probabilità complementare

(Complementary Cumulative Distribution Function) risulta:

[ ]

{

}

{

m

}

(

( )

)

N Q n x PAR P ( ) >γ2 =1− 1−2 γ (1.34) La Figura 1.6 mostra l’ andamento della CCDF del PAR per diversi valori di N e la CCDF del PAR di un vettore di campioni gaussiani e indipendenti. Come si può notare l’assunzione di gaussianità per le statistiche del PAR risulta valida.