Capitolo 2
DESCRIZIONE DEL SISTEMA IN STUDIO
2.1 Generalità
Questa tesi prende in esame lo studio del drive-train di un motore per motorscooter di 850cc. di cilindrata, bicilindrico con disposizione a V, quattro tempi, avente potenza e coppia motrice massime, rispettivamente di 52.39 Kw e 77.25 N⋅m, rilevate entrambe ad un regime di 7250 giri 1'.
E’ possibile che durante i primi test su strada, effettuati dai collaudatori dell’azienda, si evidenzi la presenza di fastidiose oscillazioni longitudinali del veicolo, nei casi di marcia a bassa velocità con il motore prossimo al regime di giri minimo, vale a dire 1270 giri 1'. Si rende dunque necessario uno studio più accurato del fenomeno, visto
che non sono certamente accettabili condizioni di questo tipo, le quali oltre ad abbassare il comfort di marcia possono compromettere il buon funzionamento dell’intera trasmissione. E’ stato inserito un elemento in gomma tra la ruota posteriore del veicolo e la puleggia condotta della cinghia dentata (Figura 2-1), in modo da modificare la risposta dinamica del sistema. Come ben noto, questo materiale, oltre ad avere una propria rigidezza è in grado di fornire un certo grado di smorzamento. Sarà proprio l’azione contemporanea di questi due fattori che avrà il compito di abbassare ad un livello accettabile le vibrazioni torsionali dell’intera trasmissione.
A questo punto si è capita l’importanza di avere un semplice mezzo che potesse dare alcune informazioni sul comportamento dinamico del drive-train durante lo svolgimento del progetto, ancor prima di avere la possibilità di effettuare test
In questo lavoro di tesi per prima cosa è stata analizzata la trasmissione allo scopo di rilevare tutti quei valori che ne permettessero uno studio dinamico.
2.2
Descrizione del drive train
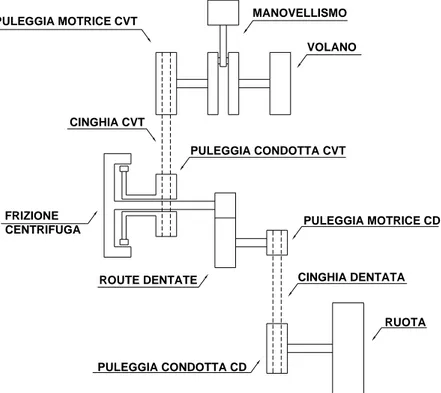
CINGHIA CVT CINGHIA DENTATA VOLANO MANOVELLISMO RUOTA ROUTE DENTATE PULEGGIA MOTRICE CD PULEGGIA CONDOTTA CD PULEGGIA MOTRICE CVT PULEGGIA CONDOTTA CVT FRIZIONE CENTRIFUGA
Figura 2-1 – Schema del drive-train
In Figura 2-1 sono evidenziati gli elementi principali che costituiscono il nostro oggetto di studio. Come abbiamo precedentemente accennato si tratta di un motore bicilindrico con disposizione a V. Le due bielle sono montate affiancate sulla medesima manovella e quindi si capisce come i cilindri siano disassati l’uno dall’altro Si nota come l’albero motore completo di tutte le masse alterne sia connesso da un lato con il volano, responsabile di regolare il funzionamento del propulsore, e dall’altro con la puleggia motrice del cambio di velocità. Quest’ultimo si tratta di un cambio a variazione continua del rapporto (CVT), soluzione ormai consueta per questo tipo di veicoli. Successivamente troviamo la puleggia condotta del CVT, della quale fanno parte anche le 5 massette delle frizione centrifuga. E’ stata adottato questo tipo di frizione in luogo di una tradizionale per la sua estrema funzionalità; come ormai si fa da molti anni. La campana andrà a connettersi con la prima delle due ruote dentate che costituiscono un’ulteriore riduzione della velocità. A questo
punto troviamo l’ultima riduzione, della quale è responsabile una cinghia sincrona tramite due pulegge dentate. Come ultimo elemento troviamo ovviamente la ruota posteriore dello scooter.
Quindi, nel percorrere la trasmissione, la velocità di rotazione dell’albero motore subisce ben tre variazioni. La prima viene effettuata dal CVT, il quale può imprimere un rapporto variabile che va da 0.831 ( marcia lunga ) a 2.079 ( marcia corta ) che indichiamo con τcvt. La seconda è realizzata dalla coppia di ruote dentate, che hanno rispettivamente 23 e 59 denti e quindi applicano una riduzione di 2.565, al quale diamo il nome di τ. Infine l’ultima permette un ulteriore rallentamento della velocità angolare di 2.300 volte, visto che le pulegge dentate hanno 30 e 69 denti, che andiamo a chiamare τcd.
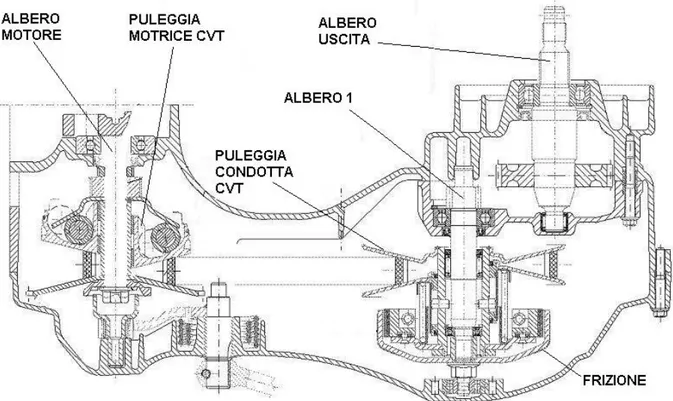
Per comprendere meglio lo schema del drive train, in Figura 2-2 si riporta un esempio tipico di una trasmissione di un motorscooter.
Figura 2-2 – Esempio di una trasmissione di un motorscooter
Si notano chiaramente i componenti principali che si ritrovano anche nello schema presentato sopra. In questo esempio tuttavia non sono rappresentati alcuni componenti, che rischiavano solo di rendere più difficile la comprensione del disegno. Non sono stati riportati: il volano connesso all’albero motore, le masse
alterne, le due riduzioni, effettuate dalle ruote dentate e dalla cinghia sincrona, che si trovano tra l’albero 1 e l’albero di uscita, e la ruota posteriore.
Noto questo possibile layout del drive train è stato affrontato il problema di come schematizzare il sistema per poterlo studiare .
2.3
Schematizzazione del drive train
J
1J
3J
2J
6J
8J
10J
5J
7J
9K
1K
2K
4K
3K
5K
6J
4τ
cvtτ
τ
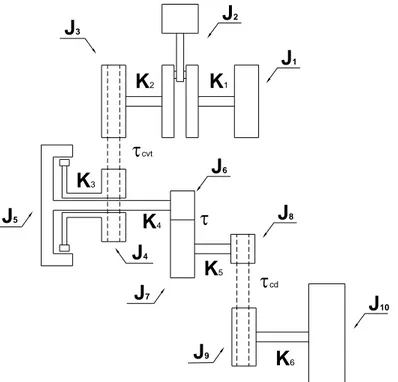
cdFigura 2-3 – Schema del drive-train
Per schematizzare il sistema si è pensato di ridurre ogni suo componente ad un volano avente lo stesso momento di inerzia polare rispetto al proprio asse di rotazione. Sono state poi calcolate le rigidezze degli alberi che connettono l’uno all’altro i vari membri del drive train. In Figura 2-3 è mostrato come sono stati denominati i componenti.
2.3.1 Momenti d’inerzia
Volano: dopo aver effettuato delle misurazioni sperimentali il suo momento d’inerzia
è risultato 6
1=6600⋅10−
J Kg⋅m2
.
Manovellismo: per il calcolo del momento d’inerzia del manovellismo devono essere
considerati molti fattori. Partendo dall’albero motore bisogna tener presente le due maschette, l’asse di accoppiamento di queste sul bottone di manovella e il cuscinetto di strisciamento sul quale ruotano le due bielle. Non va inoltre dimenticato il contributo dei pistoni, degli spinotti e delle bielle.
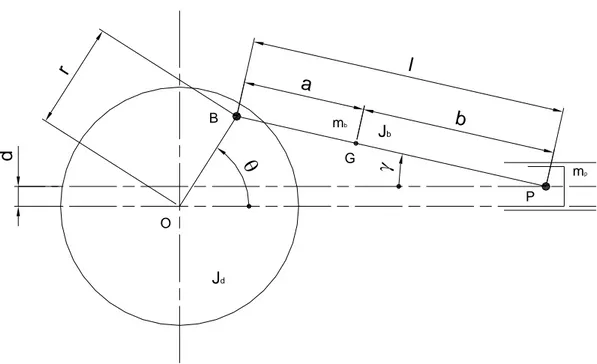
La Figura 2-4 mostra un sistema biella manovella dove J e b J sono i momenti d d’inerzia della biella (attorno al suo centro di gravità G) e delle maschette, m ed p m b le masse del pistone, completo di spinotto, e della biella. Con r si è indicato il raggio di manovella. E’ abitudine sostituire la biella con un sistema formato da due masse
1
m e m2, poste rispettivamente nel perno di manovella B e nello spinotto del pistone
P, ed un momento d’inerzia J . Con queste tre condizioni è lecito scrivere 0
l b m m1= b ; l a m m2 = b ; J =Jb −
(
ma +m b)
=Jb −mbab 2 2 2 1 0 (1)Inoltre si definiscono i parametri
l r = α β =d l (2) e le funzioni
( )
( )
( )
( )
( )
( )
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + = γ θ β γ θ α θ θ cos cos cos 2 2 sin sin 1 f( )
( )
( )
2 2 2 cos cos ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = γ θ α θ f (3)γ
θ
mp mb G P B Jd O Jb a b l r dFigura 2-4 – Schema del meccanismo biella-manovella
Come proposto da G. Genta [3] tutto il meccanismo può essere modellato, dal punto di vista dell’energia cinetica, con un singolo momento d’inerzia variabile con l’angolo di manovella Jeq
( )
θ , che ruota con la velocità angolare θ& .(
)
( )
( )
[
]
( )
2 2 0 1 2 2 2 1 2 2 1 2 1θ& θ θ θ θ& eq p d c J mr m m r f J f J E = + + + + = (4)Nello studio delle vibrazioni torsionali il moto di ciascuna sezione dell’albero a gomiti può essere espressa con la sovrapposizione della rotazione del corpo rigido con velocità angolare ω ed un moto vibrazionale espresso dalla rotazione torsionale
( )
tz
Φ . Dal momento che l’angolo θ può essere espresso come θ
( )
t =ωt+Φz( )
t , l’energia cinetica è( )
(
)
2 2 1 z eq c J t E = θ ω +Φ& (5)La (5) è valida in generale, anche se la velocità media dell’albero ω varia nel tempo; nei calcoli seguenti sarà ipotizzata soltanto una velocità di rotazione costante e le derivate di omega rispetto al tempo saranno trascurate.
L’equazione del moto della manovella in termini della coordinata generalizzata Φz
( )
t può essere ottenuta dall’equazione di Lagrange(
)
J( )
M Jeq z eq = ∂ ∂ Φ + + Φ θ θ ω 2 2 1 & && (6)dove M è il momento dovuto a tutte le azioni esterne sul sistema, compresi elasticità e smorzamenti.
La (6) è un’equazione differenziale del secondo ordine in Φz. Non è lineare sia se
M è una funzione lineare rispetto alla coordinata generalizzata Φz, come nel caso in cui l’albero abbia una un comportamento lineare elastico, che rispetto alla sua derivata. Quest’ultimo caso si presenta se il sistema è smorzato linearmente visto che i suoi coefficienti dipendono sia dal tempo che da Φz.
A questo punto è lecito porre delle semplificazioni all’equazione del moto del meccanismo biella-manovella con lo scopo di ottenere un’equazione lineare a coefficienti costanti. La prima è quella di sostituire un momento d’inerzia Jeq costante
nel termine JeqΦ&& al valore effettivo che è una funzione di θ . La seconda è quella di z
considerare che l’angolo Φz sia così piccolo da poter essere trascurato nell’espressione di θ nel secondo termine dell’equazione (6).
Si ottiene quindi
( )
( )
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ − = Φ t t J M Jeq z eq ω ω ω2 2 1 && (7)L’ultimo termine di (7) è indipendente sia dall’angolo Φz che dalle sue derivate, quindi è una funzione nota dell’ angolo ω e del tempo e può essere trattata come t un’eccitazione esterna applicata al sistema.
Ora è chiaro perché e sotto quali ipotesi sia lecito sostituire ogni gomito con un momento d’inerzia costante sul quale agiscono le coppie d’inerzia, variabili nel tempo secondo una storia temporale nota, e le effettive forze esterne dovute al fluido operante. E’ da notare che per lo studio delle oscillazioni libere del sistema si ricorre all’equazione omogenea associata alla (7), la quale non tiene conto di tali forze
d’inerzia, dovute alla variazione di J rispetto a eq θ e quindi prende in considerazione
soltanto il momento d’inerzia medio Jeq.
L’espressione utilizzata per il calcolo di quest’ultimo è [3]:
(
)
0 0 2 2 0 2 1r a m m r J c m J Jeq = d + + + p + (8) con(
)
(
)
16 1 8 6 1 2 8 2 2 2 2 4 0 α β β β α + + + + + = a (9)(
)
8 4 6 1 4 2 2 2 2 0 β β α α + + + = c (10)A questo valore bisogna sommarci il contributo del perno di accoppiamento delle due maschette e quello del cuscinetto di strisciamento.
La massa del perno (Figura 2-6 ) è stata calcolata tramite l’equazione
(
)
(
)
4 2 2 ' 2 ' ρ π D d b a Mperno = − + (11)adove ρ è il peso specifico dell’acciaio che vale 7850 Kg m3
, ed assume un valore di 7816 . 0 = perno M Kg
Il momento d’inerzia risulta quindi
(
)
(
)
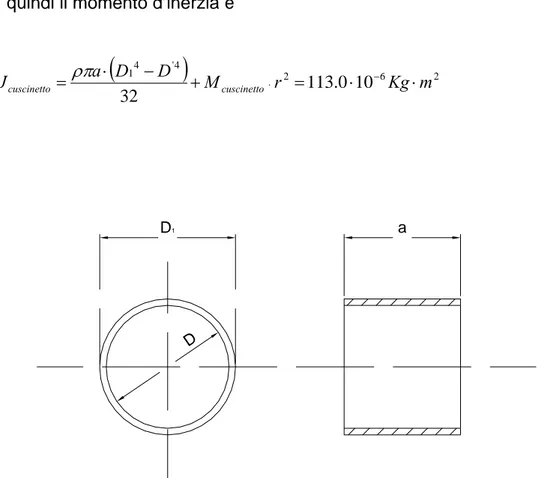
2 6 2 4 ' 4 ' 10 4 . 1093 32 2 m Kg r M d D a b Jperno = + − + perno = ⋅ − ⋅ ⋅ ρπ (12)Il cuscinetto (Figura 2-5) ha una massa di
a
(
D D)
a Kg Mcuscinetto 0.0710 4 2 ' 2 1 = ⋅ − =π ρ (13)E quindi il momento d’inerzia è
(
)
2 6 2 4 ' 4 1 10 0 . 113 32 M r Kg m D D a Jcuscinetto = ⋅ − + cuscinetto = ⋅ − ⋅ ⋅ ρπ (14) D1 D aFigura 2-5 – Cuscinetto di strisciamento
A questo punto è possibile calcolare il momento d’inerzia totale che compete ad entrambi i cilindri tramite la seguente equazione
cuscinetto bottone
eq J J
J
J2 = + + (15)
Dunque il suo valore è
2 6
2 9708 10 Kg m
Puleggia motrice CVT: dopo aver effettuato delle misurazioni sperimentali il suo
momento d’inerzia è risultato 6 2
3 9400 10 Kg m
J = ⋅ − ⋅
.
Puleggia condotta CVT: il valore del suo momento d’inerzia comprende anche
quello delle 5 massette della frizione, dalle misurazioni sperimentali è stato ottenuto
2 6
4 22760 10 Kg m
J = ⋅ − ⋅
.
Campana frizione: valore misurato 6 2
5 20900 10 Kg m
J = ⋅ − ⋅
.
Ruote dentate: valori misurati 6 2
6 160 10 Kg m J = ⋅ − ⋅ e 6 2 7 2480 10 Kg m J = ⋅ − ⋅ .
Puleggia motrice cinghia dentata: valore misurato 6 2
8 1800 10 Kg m
J = ⋅ − ⋅
.
Puleggia condotta cinghia dentata: valore misurato J9 =53800⋅10 6 Kg⋅m2 −
.
Ruota posteriore: in quest’ultimo componente del nostro schema in studio è stata
considerata anche l’inerzia dell’ intero veicolo compreso il pilota. Il valore è stato calcolato con la seguente equazione
(
Mveicolo Mpilota)
Rr JpnJ = + 2 +
10 (16)
Dove
Mveicolo= massa veicolo= 263 Kg
Mpilota= massa pilota= 75 Kg
Rr= raggio rotolamento ruota = 285 mm
Jpn= inerzia dell’insieme ruota = 518000 10-6 Kg⋅m2
Si è giunti all’equazione (16) tramite le seguenti semplici considerazioni:
se il veicolo, compreso di passeggero, accelera sarà sottoposto ad una forza d’inerzia che vale
(
)
t V M M Fi veicolo pilota ∂ ∂ + = (17)(
veicolo pilota)
r(
veicolo pilota) (
R r)
r i R t R M M R t V M M M ∂ ⋅ ∂ + = ∂ ∂ + = ω (18) Dove si è sostituito r R R V =ω ⋅ (19)con ωR =velocità angolare ruota
Si ottiene dunque
(
)
( )
t R M M M R r pilota veicolo i ∂ ∂ + = 2 ω (20)Per il teorema del momento assiale della quantità di moto si può dire che l’inerzia del veicolo completo di pilota si può esprimere come
(
)
2 r pilota veicolo veicolo M M R J = + (21)Il valore dell’ultima inerzia è dunque
27972050 10 = J 6 2 10 Kg⋅m ⋅ − 2.3.2 Rigidezze alberi
Albero motore: come propone G.Bocchi nel manuale sui motori a quattro tempi [4]
l’albero motore può essere ridotto ad un albero avente un diametro a nostro piacimento ed una lunghezza, detta lunghezza equivalente, tale da presentare le stesse caratteristiche elastiche dell’albero a gomito. Una volta scelta l’entità del diametroDe, di solito dello stesso valore dei perni di banco, si può calcolare la
lunghezza equivalente tramite la formula di Carter
5 . 1 75 . 0 8 . 0 2 s b r d D a D b c D Lr ⋅ + − + ⋅ = (22)
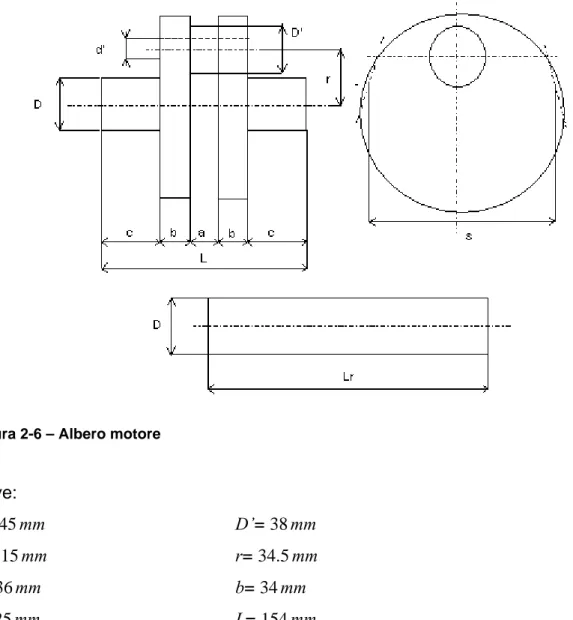
La Figura 2-6 mostra l’albero motore del bicilindrico studiato.
Figura 2-6 – Albero motore
Dove:
D= 45mm D’= 38mm
d’= 15mm r= 34.5mm
a= 36mm b= 34mm
c= 25mm L= 154mm
E’ stato scelto come diametro dell’albero equivalente quello dei perni di banco, vale a dire De=45mm, la lunghezza equivalente assume quindi un valore di
01 . 136 = r L mm
Con il valore della lunghezza e del diametro è ora semplice calcolare la rigidezza torsionale dell’albero equivalente tramite la formula
1000 0 ⋅ ⋅ = r m L J G K (23)
Dove G è il modulo di elasticità tangenziale dell’acciaio e J0 il momento d’inerzia della
sezione dell’albero.
Utilizzando i seguenti valori
80000 = G N mm 4 4 0 402578 32 mm D J =π⋅ e = (24) si ottiene 236785 = m K N⋅m rad
K1: per il calcolo di questa rigidezza torsionale bisogna prendere in considerazione
sia il tratto di albero che connette volano e albero motore, che il contributo della rigidezza dell’albero motore stesso
Si è ridotto il complesso cilindri-albero motore ad un volano di momento d’inerzia polare J2 con connessi due alberi di rigidezza torsionale Kmm. Tale valore è stato
calcolato considerando questi due alberi come due molle in parallelo aventi come risultante Km (Figura 2-7) e risulta
rad m N K Kmm= m =118392.5 ⋅ 2 (25)
J
2K
mmK
mmJ
2K
mmK
1J
1J
3K
mmK
2Figura 2-8 – Schema equivalente manovellismo-volano-puleggia motrice CVT
A questo punto è stata calcolata la rigidezza torsionale K del tratto di albero che 1
connette il volano con l’albero motore (Figura 2-7 e Figura 2-8) e considerata in serie alla Kmm in modo da ottenere la K1 del nostro modello semplificato (Figura 2-9).
K
1J
1J
2J
3K
2Il calcolo di K è stato effettuato tramite il metodo descritto da G.Rossi [5]. 1
A
H
G
F
B
C
D
E
Figura 2-10 – Albero di collegamento tra volano e albero motore
A= 40 mm B= 27 mm C= 8 mm
D= 15 mm E= 25 mm F= 10 mm
G= 45 mm H= 5 mm
Sia per questo che per il resto degli alberi si fa riferimento ad un diametro dell’albero equivalente di De=45 mm, come abbiamo già fatto per l’albero motore. Come prima cosa si calcolano le lunghezze dei vari tratti di albero aventi diametri differenti. Per il tratto H si ha ( Figura 2-10 )
(
)
mm C A H D Lr 4e 4 8.0 4 1 = − ⋅ = (26)Per il secondo (G) vista una differenza diametrale non trascurabile fra i due tronchi bisogna considerare un fattore maggiorativo λ [5]. Quest’ultimo si ricava tramite un grafico dopo aver quantificato la grandezza
481 . 1 =
Nel nostro caso assume un valore di
λ= 22.41 mm
Ora è possibile calcolare la lunghezza equivalente con la formula seguente
(
)
(
)
mm C B G D Lr e4 4 524.2 4 2 = − + = λ (27)Il terzo tratto (F) data la sua trascurabile conicità può essere considerato cilindrico con un diametro I =26mm in modo da ottenere
(
)
mm D I F D Lr 4e 4 100 4 3 = − ⋅ = (28)La lunghezza equivalente dell’albero sarà uguale alla somma delle tre appena trovate mm L L L Lr= r1+ r2+ r3=632.2 (29)
Da questo valore si può ricavare la rigidezza torsionale K1 dell’albero tramite la
formula 50943 1000 0 1 = ⋅ ⋅ = r L J G K N⋅m rad
Utilizzando la formula delle molle in serie si giunge infine al valore di K1
rad m N K K K K K mm mm ⋅ = + ⋅ = 35617 1 1 1 (30)
K2: si procede nello stesso modo in cui si è calcolata la precedente rigidezza
mostra le dimensioni del tratto di albero che connette l’albero a gomito con la puleggia motrice del CVT.
A
F
E
D
B
C
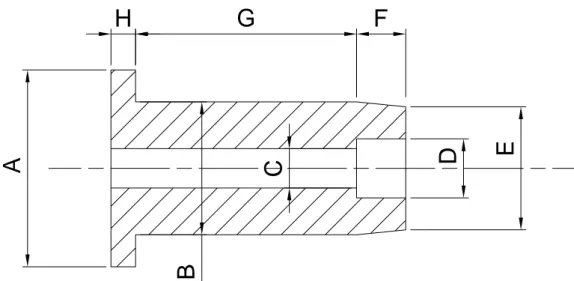
Figura 2-11 – Albero di collegamento tra albero motore e puleggia motrice CVT
Si procede al calcolo delle lunghezze dei vari tronchi in modo da ottenere quella equivalente. 8 4 4 1 = ⋅ = A F D Lr e mm
Per ottenere Lr2 e Lr3 è necessario ricavarsi i valori di λ1 e λ2 che dipendono
rispettivamente dai rapporti fra i diametri
143 . 1 = C A 400 . 1 = B C ed hanno un valore di λ1= 12.25 mm λ2= 18.75 mm
(
)
5 . 75 4 1 4 2 = + = C E D Lr e λ mm(
)
721.7 4 2 4 3 = + = B D D Lr e λ mmLa lunghezza equivalente sarà
2 . 804 3 2 1+ + = = r r r r L L L L mm
Che condurrà ad una rigidezza torsionale
40048 1000 0 2 = ⋅ ⋅ = r L J G K N⋅m rad
Utilizzando la formula delle molle in serie si giunge infine al valore di K2
29925 2 2 2 = + ⋅ = mm mm K K K K K N⋅m rad
K3: dalla Figura 2-12 si ricavano tutti i fattori necessari per calcolare la rigidezza
torsionale dell’albero che connette la puleggia condotta del CVT al mozzo dove sono fissate le cinque massette della frizione centrifuga. Visto che si è trascurato il transitorio durante il quale c’è slittamento si può dire che questo tratto di albero colleghi in definitiva la puleggia condotta del CVT con la campana della frizione.
A
C
B
A= 40mm B= 60mm C= 54mm
Con una sola equazione si ottiene subito la lunghezza equivalente
(
4 4)
41.4 4 = − ⋅ = A C B D Lr e mmDalla quale si ricava la rigidezza torsionale K 3
777929 1000 0 3 = ⋅ ⋅ = r L J G K N⋅m rad
K4: questa è la rigidezza torsionale del tratto di albero che collega la campana della
frizione con la prima ruota dentata.
A
B
D
C
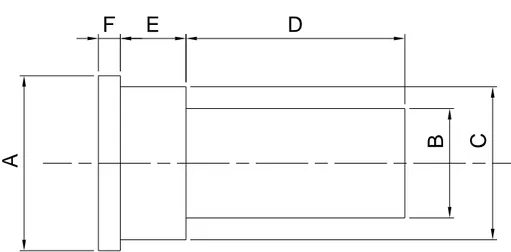
Figura 2-13 – Albero di collegamento tra la campana e la prima ruota denata
A= 46 mm B= 30 mm
C= 36 mm D= 11 mm
10 4 4 1 = ⋅ = A D D Lr e mm
Dal valore del rapporto
533 . 1 = B A
Si ricava λ=26.1 mm che ci permette di calcolare
(
)
5 . 314 4 4 2= + = B C D Lr e λ mm La lunghezza equivalente è mm L L Lr= r1+ r2=324.5 (31)Alla quale compete la rigidezza torsionale cercata
99249 1000 0 4 = ⋅ ⋅ = r L J G K N⋅m rad
K5: l’albero mostrato in Figura 2-14 è quello che connette la seconda ruota dentata
con la puleggia più piccola sulla quale si avvolge la cinghia sincrona.
B C A E D H G F
A= 38 mm B= 35 mm C= 10 mm
D= 30 mm E= 30 mm F= 60 mm
G= 10 mm H= 11 mm
Vista la presenza del foro il tratto F è stato suddiviso in due parti di lunghezza
(
)
91=D− G+H =
F mm F2=F−
[
D−(
G+H)
]
=51mm (32) La lunghezza equivalente del tratto G è(
4 4)
19.8 4 1 = − ⋅ = C A G D Lr e mmPer i tratti H e F1 una volta calcolati i rapporti
09 . 1 = B A 27 . 1 = E A
Ai quali corrispondono i coefficienti maggiorativi
λ1= 8.05mm λ2= 17.70 mm si ricava
(
)
(
4 4)
1 52.4 4 2 = − + = C B H D Lr e λ mm(
(
4 1 4)
2)
52.8 4 3 = − + = C E F D Lr e λ mmInfine per il tratto F2 si ha
2 . 258 4 2 4 4= ⋅ = E F D Lr e mm
La lunghezza equivalente è, come al solito
mm L L L L Lr= r1+ r2+ r3+ r4=383.2 (33)
Alla quale corrisponde 84046 1000 0 5 = ⋅ ⋅ = r L J G K N⋅m rad
K6: è la rigidezza dell’albero che collega la seconda puleggia dentata con il mozzo
della ruota posteriore dello scooter. Dopo prove sperimentali effettuate dall’azienda è risultata avere un valore di
194238
6=
K N⋅m rad
In Tabella1 e Tabella 2 sono raccolti tutti i parametri che definiscono il drive train.
Tabella 1 – Momenti d’inerzia del drive train
Componente Momento d’inerzia
2 m Kg⋅ Volano 1 6600 10 6 − ⋅ = J Manovellismo 2 9708 10 6 − ⋅ = J Puleggia motrice CVT 3 9400 10 6 − ⋅ = J Puleggia condotta CVT 4 22760 10 6 − ⋅ = J Campana frizione 5 20900 10 6 − ⋅ = J Ruota dentata 6 160 10 6 − ⋅ = J Ruota dentata 7 2480 10 6 − ⋅ = J
Puleggia motrice cinghia dentata 8 1800 10 6 −
⋅ =
J
Puleggia condotta cinghia dentata 9 53800 10 6 − ⋅ = J Ruota posteriore 10 27972050 10 6 − ⋅ = J
Tabella 2 – Rigidezze torsionali degli alberi del drive train
Simbolo Rigidezza torsionale
rad m N⋅ 1 K 35617 2 K 29925 3 K 777929 4 K 99249 5 K 99249 6 K 194238