2. Il solver NEC.

2. Il solver NEC.

2.1 Funzionamento del solver.

Il Nec2 è un solver che utilizza come metodo di calcolo il Metodo dei Momenti (MoM) e consente di simulare il comportamento di una qualunque antenna radiante implementabile mediante strutture filari.

Il file di input del programma è composto da una sequenza di comandi denominati card che permettono di definire le caratteristiche fisiche ed elettriche di ciò che si intende implementare. Si riporta di seguito un esempio di file input che sfrutta le card di base del software e descrive un semplice monopolo posto su piano di massa a cui è fornita un’alimentazione di tipo tensione:

GW 1 45 0.0 0.0 0.75 0.0 0.0 0.0 0.002 GE 1 EX 0 1 23 0 1 0 GN 1 FR 0 1 0 0 100 0 EN

La card GW permette di descrivere qualunque filo rettilineo conduttore. La struttura prevista è la seguente

GW,ITG,NS,XW1,YW1,ZW1,XW2,YW2,ZW2,RAD

dove compaiono, in sequenza, l’intero identificativo del segmento, il numero di sub-segmenti in cui esso è suddiviso, le coordinate dell’estremo iniziale, quelle dell’estremo finale ed infine il raggio del filo.

L’unità di misura scelta è il metro, e, nel caso si faccia riferimento ad una diversa unità di misura, si può ricorrere alla card GS che consente di effettuare una scalatura opportuna sulle dimensioni della struttura di partenza.

Come accennato ogni filo è identificato da un intero chiamato tag che ne rende più semplice ed immediato il riconoscimento ed è inoltre suddiviso in un numero di sub segmenti che consente di rispettare le limitazioni imposte sulla lunghezza di ognuno di essi, legate al fatto che il Metodo

dei Momenti è basato sul calcolo delle correnti su piccoli segmenti.

Devono, infatti, essere rispettate le seguenti condizionI:

• D ≤ λ/10, essendo D la lunghezza del sub segmento e λ la lunghezza d’onda;

• 2 π a << λ ( con a raggio della sezione del conduttore), per fare in modo che, così come previsto dal modello elettromagnetico, i conduttori filari abbiano una corrente con sola componente assiale senza alcuna variazione lungo la circonferenza del filo stesso. • D/a>8, al fine di poter considerare un filamento di corrente localizzata sull’asse del

conduttore.

Le eccitazioni applicate sono fornite dalla card EX. Esse possono essere di tipo onda piana, corrente o tensione applicata e nella loro dichiarazione si deve far riferimento, oltre che alla loro intensità in parte reale (F1) e parte immaginaria (F2), al tag (I2) e al subsegmento (I3) di tale tag a cui esse vengono applicate:

EX,I1,I2,I3,I4,F1,F2,F3

dove I1 viene posto uguale a zero quando la sollecitazione è di tipo tensione e I4 è un comando

per la stampa sul file di uscita dei valori dell’impedenza al variare della frequenza.

Il piano di massa perfettamente conduttore è inserito tramite la card GN nella forma GN,1. In aggiunta deve essere specificata la card GE nelle forme:

• GE,0 se non è presente il piano di massa

• GE,1 se è presente il piano e vi sono conduttori con un estremo

appartenente al piano in cui si ha un’interpolazione della corrente con l’immagine che sta sotto al piano

• GE,-1 se si vuole forzare a zero la corrente nell’estremo del conduttore

appartenente al piano di massa.

Infine, per effettuare un’analisi nel dominio frequenziale ad una frequenza fissa, la card da usare è la FR nella forma:

FR,0,1,0,0,FREQ(MHz),0,0

La card EN è l’ultima della descrizione ed indica al programma la fine dell’esecuzione.

Quelle appena definite sono le istruzioni usate nei file di input del solver per effettuare le simulazioni riportate nei capitoli successivi.

Per comprendere in maniera più approfondita il funzionamento del NEC e il passaggio dalla formulazione numerica del problema ai risultati ottenibili dalle simulazioni, si illustrerà il principio alla base del solver, il Metodo dei Momenti.

2.2 Il Metodo dei Momenti (MoM)

Il Metodo dei Momenti è una delle tecniche che permette di risolvere numericamente il problema legato alla determinazione del campo elettromagnetico, riconducendolo alla risoluzione numerica di una o più equazioni integrodifferenziali, le cui soluzioni dipendono dalle condizioni iniziali e da quelle al contorno. La tecnica è basata sulla riduzione di tali equazioni ad un sistema di equazioni lineari su cui viene applicato il metodo dei residui pesati, come mostrato in [5].

Le equazioni risolte mediante la tecnica del metodo dei momenti sono generalmente una forma dell’equazione integrale del campo elettrico (electrical field integral equation, EFIE) o del campo magnetico (magnetic field integral equation, MFIE), entrambe ricavabili dalle equazioni di Maxwell considerando il problema di un campo scatterato da un conduttore perfetto (o da un dielettrico privo di perdite).

La forma dell’equazione integrale usata determina quale tecnica sia maggiormente adatta alla risoluzione del problema. Ad esempio, un’equazione del tipo EFIE può essere particolarmente adatta per la modellizzazione di una struttura filare.

Lo scopo di questo capitolo è quello di fornire dei cenni alla teoria del MoM, al fine di fornire una descrizione più dettagliata del solver NEC e fornire indicazione sull’utilizzo che ne è stato fatto.

2.3 Teoria alla base del Metodo dei Momenti

L’obiettivo è quello di risolvere un’equazione non omogenea del tipo

( )

f g

L = (2.1)

dove L

( )

• rappresenta un operatore lineare, g il termine noto (eccitazione) e f è la funzione incognita da determinare (campo).

Il primo passo nel processo di soluzione implementato dal MoM consiste nell’espansione di f mediante funzioni di base appartenenti al dominio dell’operatore lineare, secondo opportune costanti. A questo scopo si riduce f alla forma:

n N i n n f f =

∑

⋅ = α . (2.2)

Essendo la sommatoria ridotta ad un numero finito di elementi, la (2.2) fornisce un’approssimazione della funzione stessa.

Sfruttando la linearità di L e combinando la (2.1) e la (2.2) si ottiene:

( )

f L f L

( )

f g L N _n n n N n n n ⎟= ⋅ = ⎠ ⎞ ⎜ ⎝ ⎛ _⋅ =

∑

∑

= =1 1 α α (2.3) .

Essendo a questo punto definito l’insieme delle funzioni di base, L

( )

f_n , il problema si riduce alla determinazione degli N coefficienti incogniti α_n e quindi alla soluzione di N equazioni

linearmente indipendenti, ottenibili tramite due distinte metodologie: il metodo delle Weighting Functions e il metodo del Point-Matching.

2.3.1 Il metodo Weighting Functions.

Questo metodo prevede l’individuazione di M funzioni di peso w₁,w₂,....w_M e la particolare scelta w_n = f_n è nota come “metodo di Galerkin”.

Definito il prodotto interno fra due funzioni f e g, f ,g , questa deve soddisfare, oltre alle proprietà di simmetria e linearità le seguenti relazioni:

0 , f > f se f ≠0 0 , f = f se f =0

si sceglie pertanto un’espressione del prodotto interno adatta al problema. Una possibile scelta è la seguente

( ) ( )

x g x dx f f f S • =

_∫

,

dove S è il dominio di esistenza delle funzioni f

( )

x e g

( )

x .

Nel metodo dei momenti il prodotto interno viene effettuato fra l’equazione non omogenea ed ogni funzione di peso w , ottenendo: _n

( )

f w L f w L

( )

f w g L w N _{m n m} n n N n n n m m, , , 1 1 = • = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _• =

∑

∑

= = α α (2.4)

Il sistema ad M equazioni lineari nelle incognite α_n ottenuto è esprimibile in forma matriciale come

[ ] [ ] [ ]

lmn • αn = gm (2.5)

dove l_mn = w_m,L

( )

f_n ,

[ ]

α_n è il vettore dei coefficienti, e

[ ]

g_n = w_n,g .

Dal momento che, per M=N, la matrice

[ ]

l_mn non è singolare, esiste la sua inversa, da cui è possibile risalire ai coefficienti incogniti.

La soluzione che in tal modo si ottiene potrà ovviamente essere approssimata, dipendentemente dalla scelta delle funzioni di base e di peso che dovranno essere linearmente indipendenti e scelte in modo da ridurre il tempo di calcolo di

[ ]

l_mn e

[ ]

g rispettivamente. _n

2.3.2 Il metodo del Point-Matching.

Questo metodo consente di rendere più agevole la scelta degli elementi della matrice

[ ]

lmn e del vettore

[ ]

g , usando le funzioni di Dirac come funzioni di prova. È questo il metodo m

utilizzato dal solver NEC.

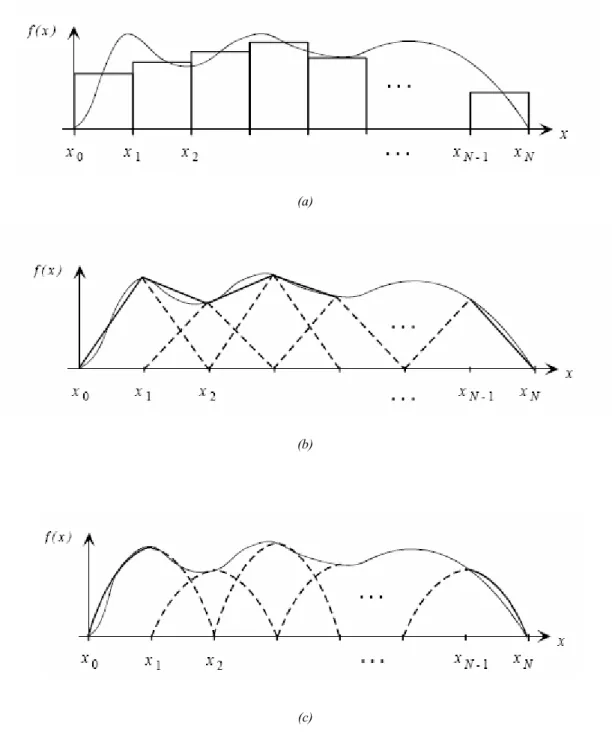
In questo caso le funzioni di base f₁,f₂,...f_Nvengono scelte in modo da permettere un’esatta ricostruzione della funzione f(x) che ha un andamento arbitrario lungo l’asse x. A tale scopo si possono usare funzioni di base che possono essere definite su sottodomini o sull’intero dominio. Si riportano alcuni esempi di funzioni base per l’approssimazione della funzione incognita (figura 2.3.1). Nel primo caso le funzioni interpolanti sono ad impulso rettangolare, nel secondo caso sono di tipo triangolare, ed infine si possono utilizzare, come nel terzo caso, funzioni con andamento sinusoidale a tratti, dette PWS (Piece Wise Sinusoidal).

(a)

(b)

(c)

Fig 2.3.1: esempi di funzioni base per approssimare la funzione incognita: (a) impulsi rettangolari, (b) impulsi triangolari, (c) funzioni PWS.

Il NEC usa le tecniche del MoM basate sulla risoluzione numerica delle equazioni integrali per le correnti indotte su strutture metalliche da sorgenti o da un campo incidente.

Dal momento che il MoM è basato sul calcolo di correnti su piccoli segmenti e che questo problema è formulato in forma matriciale, il tempo di calcolo aumenta all’aumentare del numero

di segmenti, che dipende dalle dimensioni della struttura e dalla frequenza. Infatti, generalmente, è da ritenersi una buona scelta quella per cui ogni segmento presenti una lunghezza di un decimo di lunghezza d’onda.

Si prenda in esame un oggetto conduttore isolato posto nello spazio vuoto in un riferimento cartesiano. Se la sorgente elettromagnetica si trova sull’oggetto si tratterà di un problema di antenna, se è lontana dal corpo, invece, di un problema di reirradiazione (scattering).

Si definiscono con E e _i H i campi elettrico e magnetico incidenti, valutati in assenza del corpo _i

conduttore, sul quale scorre una corrente con densità j e distribuzione di carica ρ che produce _s

un campo riflesso E e _s H . La somma delle rispettive componenti fornisce il campo totale in un _s

generico punto del riferimento cartesiano xyz:

s i s i E H H H E E = + , = + (2.6)

Il campo totale sarà calcolato come somma del campo reirradiato, calcolato tramite le equazioni di Maxwell a partire dalla conoscenza di ρ e J e del campo incidente. _s

Nel sistema di riferimento adottato si indicano con r,r',nˆ _{i vettori che individuano} rispettivamente il punto in cui si vuole calcolare il campo, quello sulla superficie del conduttore e il versore normale alla superficie (figura 2.3.2).

Fig 2.3.2: sistema di riferimento adottato.

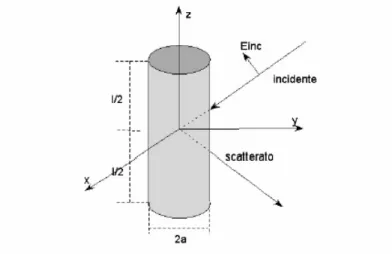
Si consideri ora un’onda piana monocromatica incidente sul filo, perfettamente conduttore, di lunghezza l. La figura 2.3.3 mostra il campo incidente e quello reirradiato.

Fig 2.3.3: campo incidente e riflesso su un conduttore filare di lunghezza l.

Utilizzando le terza equazione di Maxwell e introducendo il potenziale vettore A, il campo reirradiato sarà: A Hs =− ∇× µ 1 (2.7)

e

(

)

[

k A A

]

j Es ₌₋ 1 2 _+∇∇• ωεµ , (2.8)

dove k =ω µε , costante di propagazione.

Essendo la corrente distribuita unicamente lungo l’asse z e riportando il tutto ad un sistema di coordinate cilindriche, si ottiene:

ϕ ρ µ a A Hs z ∂ ∂ − = 1 _(2.9)

e, quindi, dall’equazione di Maxwell

s s _H j E = ∇× ωµ 1 , _(2.10)

si conclude che il campo elettrico reirradiato dal dipolo ha un’espressione del tipo ,

z z s _{E a Ea}

E = _{ρ ρ} + ossia non ha componente secondo la direzione a . _ϕ

Dal momento che il dipolo è, per ipotesi, un conduttore elettrico perfetto, le condizioni al contorno impongono che sia nullo il campo elettrico totale tangente alla superficie del conduttore.

Inoltre, nell’ipotesi che sia a<<λ, dove a è il raggio del filo, si può affermare che la corrente sarà distribuita sulla superficie del filo dal momento che la densità di corrente è indipendente dall’angolo azimuthale ϕ (figura 2.3.4).

Fig 2.3.4: se a<<λ la corrente sarà distribuita sulla superficie del filo.

A seguito delle considerazioni fatte, si giunge alla formulazione, priva dei passaggi intermedi per motivi di brevità, dell’ Equazione Integrale di Pocklington [5]:

( )

( )

i z z G z z dz j E dz d k z I _⎥ =− ωε ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +

∫

− ' ' 2 2 2 2 1 2 1 , (2.11)

che rappresenta l’equazione che, una volta risolta, fornisce la corrente incognita I.

La (2.11) è un’equazione integrodifferenziale, pertanto da essa può essere ricavata la distribuzione di corrente tramite l’applicazione del MoM, esprimendola nella forma

( )

n N n n z z z I I ' 1 ) (

∑

= Λ = , (2.12)

dove Λ₁,Λ₂,...Λ_N sono le funzioni di base.

Facendo ad esempio riferimento ad una base di funzioni triangolari, la relazione fra i fasori di corrente e le funzioni base aventi dominio sulle sottosezioni del filo, è mostrata in figura 2.3.5

Fig 2.3.5: esempio di espansione in serie della corrente tramite funzioni triangolari.

Il problema è stato in tal modo ricondotto alla determinazione di N coefficienti incogniti.

A questo punto si può procedere alternativamente con il metodo del Point-Matching o tramite l’operazione del Weighting.

In forma numerica il risultato avrà la forma

[ ] [ ] [ ]

Z_mn • I_n = V_m , dove

[ ]

Z_mn viene comunemente indicata come matrice delle impedenze generalizzate. Dall’inversione di quest’ultima si risale al calcolo della corrente:

[ ] [ ] [ ]

In = Zmn • Vm

−1 _.

(2.13)

Successivamente alla determinazione della corrente è possibile risalire al potenziale vettore dal quale, mediante le (2.7) e (2.8), si ottiene la distribuzione di campo elettrico e magnetico.