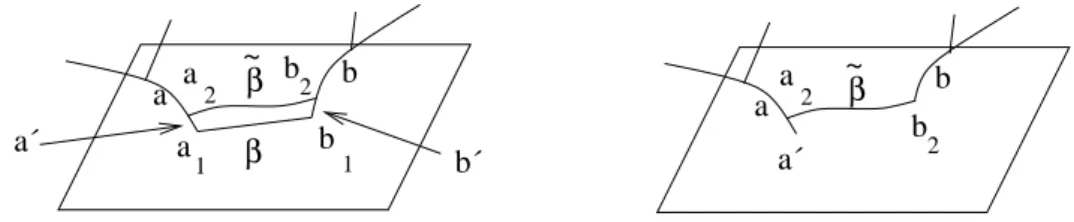Spezzamenti di Heegaard di varietà di Seifert

(1)

Indice

Introduzione 2

1 Preliminari 5

1.1 3-variet`a riducibili e ∂-riducibili . . . . 5

1.2 Superfici . . . 6

1.2.1 Superfici compressibili e ∂-compressibili . . . . 6

1.2.2 Superfici planari e gerarchie . . . 8

1.3 Manici . . . 9

1.4 Variet`a prodotto F × I . . . . 9

1.5 Posizione magra . . . 10

2 Spezzamenti di Heegaard di 3-variet`a 12 2.1 Compression body . . . 12

2.1.1 Spine di compression body . . . 14

2.2 Spezzamenti di Heegaard . . . 17 2.2.1 Stabilizzazione e riducibilità . . . 19 2.2.2 Amalgamazione . . . 23 2.3 Spezzamenti di handlebody . . . 25 2.4 Spezzamenti di F × I . . . . 27 3 Varietà di Seifert 41 3.1 Costruzione delle varietà di Seifert . . . 42

3.1.1 Gruppo fondamentale di una variet`a di Seifert . . . 45

3.2 Spezzamenti di Heegaard verticali . . . 47

3.3 Spezzamenti di Heegaard orizzontali . . . 50

3.4 Spezzamenti di F × S1 _{. . . .} ₅₃

3.4.1 Spezzamenti di F × S1 nel caso ∂F 6= ∅ e χ(F ) ≤ −1, con F 6= S2_{\ {p} 1, p2, p3} . . . . 55

3.4.2 Spezzamenti di (S2_{\ {p} 1, p2, p3}) × S1 . . . 60

3.4.3 Spezzamenti di F × S1 nel caso ∂F = ∅ . . . . 64

3.5 Spezzamenti di variet`a di Seifert con bordo . . . 70

(2)

4 Spezzamenti di Heegaard di variet`a di Seifert chiuse 80 4.1 Spezzamenti di spazi lenticolari . . . 80

(3)

Introduzione

Una 3-varietà W è un compression body se si ottiene da una varietà prodotto

F × I, con F superficie connessa compatta chiusa, attaccando 2-manici lungo

curve contenute in F × {0}, e tappando eventuali componenti sferiche venutesi a creare nel bordo della varietà risultante mediante l’attaccamento di un 3-manico. Se ∂W è connesso, W è chiamato handlebody. Il genere di W è il genere di

∂+W = F × {1} ⊂ ∂W .

Dati due compression body W1e W2dello stesso genere, sia f : ∂+W1→ ∂+W2

un omeomorfismo. Incollando W1 e W2 mediante f si ottiene una 3-variet`a M ;

questa decomposizione di M come incollamento di due compression body si chiama

spezzamento di Heegaard di M ; ogni 3-variet`a compatta il cui bordo non contenga

sfere pu`o essere costruita in questo modo.

Attualmente non è nota una caratterizzazione degli spezzamenti di Heegaard di un’arbitraria 3-varietà compatta; risultati relativi ad alcune classi particolari di 3-varietà sono stati ottenuti per la sfera S3 _{da Waldhausen ([W]), per gli spazi}

lenticolari da Bonahon e Otal ([Bon-O]) e per le varietà F × I da Scharlemann e Thompson ([ST]). È stata ottenuta poi da Moriah e Schultens ([MS]) una caratterizzazione degli spezzamenti di Heegaard per le varietà di Seifert con base orientabile.

In questa tesi sono raccolti i risultati noti relativi agli spezzamenti delle variet`a sopra citate.

Nel Capitolo 1 si d`anno alcune definizioni utili nel seguito ed alcuni enunciati che vengono assunti senza dimostrazione; si tratta di risultati generali, che trovano applicazione in vari rami della topologia geometrica. In particolare si definisce il concetto di posizione magra ([G]) di un arco (o di una curva chiusa) rispetto ad una funzione di Morse su una variet`a.

Nel Capitolo 2 viene data la definizione di compression body, dei quali viene data una nozione di spina; dopodiché si introducono gli spezzamenti di Heegaard e la proprietà di riducibilità di uno spezzamento di Heegaard. Inoltre, viene mo-strato come due 3-varietà con spezzamenti di Heegaard possano venire incollate lungo una componente di bordo in modo da ottenere uno spezzamento di Heegaard della 3-varietà risultante, mediante un procedimento chiamato amalgamazione. Il capitolo si conclude con la classificazione ([ST]) degli spezzamenti di Heegaard irriducibili delle varietà F × I, con F superficie orientabile compatta chiusa.

(4)

clas-sificazione per omeomorfismo fibrato. Le varietà di Seifert sono 3-varietà che ammettono una suddivisione in circonferenze, dette fibre, in modo che un numero finito di tali fibre, dette eccezionali, ammetta un intorno saturo tale che ogni altra fibra di tale intorno compia più di un giro intorno ad essa; tutte le altre fibre, det-te regolari, ammettono un intorno saturo tale che ogni altra fibra di tale intorno compia un solo giro intorno ad essa. Identificando fra loro i punti di una stessa fibra si ottiene una superficie, detta base della varietà di Seifert.

Uno spezzamento di una varietà di Seifert si dice verticale se ognuno dei com-pression body è un intorno regolare dell’unione di alcune componenti di ∂M con un grafo comprendente qualcuna delle fibre, e per il resto contenuto nella base della varietà.

Se da una variet`a di Seifert M togliamo un intorno di una fibra, otteniamo una variet`a M∗ _{che ammette una fibrazione su S}1 _{con fibra una superficie F ; se}

il bordo di un intorno regolare di F in M∗ _{divide M in due compression body, lo}

spezzamento di Heegaard ottenuto si dice orizzontale.

Tali spezzamenti particolari sono introdotti ancora nel Capitolo 3, e viene di-mostrato, seguendo [Schu2], che gli spezzamenti irriducibili delle variet`a di Seifert

F × S1_{, con F superficie orientabile compatta, sono verticali. A questo punto}

vie-ne definita la noziovie-ne di riducibilità verticale per uno spezzamento di una varietà di Seifert, che consente di dimostrare che gli spezzamenti irriducibili di una va-rietà di Seifert con bordo sono verticali. Ciò si ottiene, grazie ad un ragionamento induttivo, costruendo tali spezzamenti mediante amalgamazione di spezzamenti verticali ([Schu1]).

Nel Capitolo 4 vengono innanzitutto esposti i risultati di [Bon-O], che mostrano che ogni spazio lenticolare ammette un’unico spezzamento di Heegaard irriduci-bile, e questo è verticale. Infine, vengono caratterizzati ([MS]) gli spezzamenti di Heegaard nel caso più generale di varietà di Seifert con base orientabile; in par-ticolare viene mostrato che uno spezzamento irriducibile di una varietà di Seifert con base orientabile è orizzontale oppure verticale.

(5)

Capitolo 1

Preliminari

In questo capitolo saranno definiti concetti che useremo frequentemente. Inoltre saranno dati gli enunciati di alcuni teoremi che assumeremo senza dimostrazione. Definizione 1.1. Sia M una 3-varietà, e X ⊂ M è una sottovarietà propriamente

embedded. Indicheremo con η(X)e con ¯η(X) rispettivamente un intorno tubolare aperto ed uno chiuso di X in M .

Sia M una 3-variet`a orientata con bordo, e A ⊂ ∂M . Indichiamo con −M la 3-variet`a orientata data da M con l’orientazione invertita, e con −A la corrispon-dente copia di A in −M .

Definizione 1.2. Si chiama doppio di M rispetto ad A, e si indica con DA(M ),

la 3-variet`a ottenuta identificando A con −A mediante l’applicazione identica. Si chiama doppio di M , e si indica con D(M ), la 3-variet`a D_∂M(M )

Proposizione 1.3. Sia M una 3-variet`a compatta, e X una k-variet`a PL; sia

Y ⊂ X una k − 1-sottovariet`a PL di X propriemente embedded e bilatera, tale che i_∗ : π₁(Y ) → π₁(X) sia iniettiva e π₃(X) = π₂(Y ) = π₂(X \ Y ) = 0. Per ogni

mappa f : M → X esiste una mappa g : M → X omotopa a f tale che:

1. ogni componente connessa di g−1_{(Y ) `e una superficie propriamente}

embed-ded, bilatera e incompressibile in M ;

2. esistono intorni tubolari Y ×[−1, 1] di Y ∼= Y ×{0} in X e di g−1(Y )×[−1, 1]

di g−1_{(Y ) ∼}_{= g}−1_{(Y ) × {0} in M tali che g sia un omeomorfismo fra la fibra}

{p} × [−1, 1] e la fibra {p} × [−1, 1], per ogni p ∈ g−1_{(Y ).}

Dimostrazione. [H], Lemma 6.5, adattato al caso in cui π3(X) = 0.

1.1 3-variet`

a riducibili e ∂-riducibili

Definizione 1.4. Una 3-variet`a M si dice irriducibile se per ogni sfera S

em-bedded in M esiste una palla B ⊂ M tale che S = ∂B. Altrimenti, M si dice

(6)

Definizione 1.5. Una 3-variet`a si dice ∂-irriducibile se per ogni disco D

propria-mente embedded in M esistono un disco D0 _{⊂ ∂M tale che ∂D}0_{= ∂D ed una palla}

B ⊂ M tale che ∂B = D ∪ D0. Altrimenti, M si dice ∂-riducibile.

1.2 Superfici

Definizione 1.6. Diciamo che un arco α propriamente embedded in una superficie

T `e inessenziale in T se esiste un arco β ⊂ ∂T tale che α ∪ β borda un disco in T . Altrimenti α si dice essenziale. Una curva chiusa semplice γ in T si dice

inessenziale in T se è omotopicamente banale in T , altrimenti è essenziale. Definizione 1.7. Un disco propriamente embedded in una 3-varietà M si dice essenziale se ∂D è una curva essenziale in ∂M , altrimenti D si dice inessenziale. La seguente definizione introduce il concetto di spina di una superficie, come viene data in [Schu2].

Definizione 1.8. Sia G un grafo propriamente embedded in una superficie S

avente k componenti di bordo A₁, ..., A_k, e sia A = A₁ ∪ ... ∪ A_h, con h ≤ k. Poniamo X0 = X ∪ (Ah+1∪ ... ∪ Ak). Il grafo G si dice spina di S relativa ad A

se S \ X0 _{`e un intorno regolare di A.}

1.2.1 Superfici compressibili e ∂-compressibili

Definizione 1.9. Una superficie S propriamente embedded in una 3-variet`a M si

dice compressibile se vale una delle seguenti quattro condizioni: 1. S `e una sfera ed esiste una palla B ⊂ M tale che S = ∂B; 2. S `e un disco e S ⊂ ∂M ;

3. S `e un disco ed esiste una palla B ⊂ M tale che ∂B ⊂ S ∪ ∂M ;

4. esiste un disco D ⊂ M con D ∩ S = ∂D e ∂D non `e omotopicamente banale in S.

Altrimenti, diremo che S `e incompressibile.

Definizione 1.10. Sia S una superficie propriamente embedded in una 3-variet`a

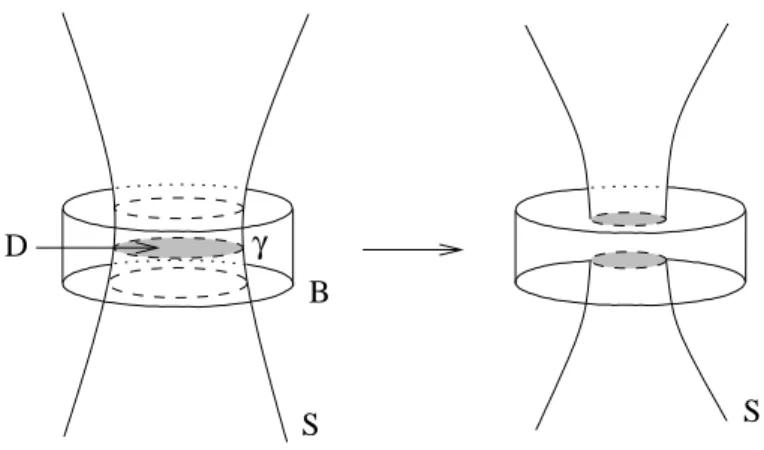
M , e sia D ⊂ M un disco con propriamente embedded in M \ S con D ∩ S = ∂D. Poniamo γ = ∂D (Figura 1.1). Una compressione lungo γ `e la seguente operazio-ne. Sia B = ¯η(D) ∼= D2× [−1, 1], in modo che D ∼= {z ∈ D2| kzk ≤ 1/2} × {0} e S ∩ B ∼= {z ∈ D2| kzk = 1/2} × [−1, 1]. Alla superficie S sostituiamo la superficie S0 tale che

S0∩ (M \ B) = S ∩ (M \ B) e

(7)

γ

S B

S D

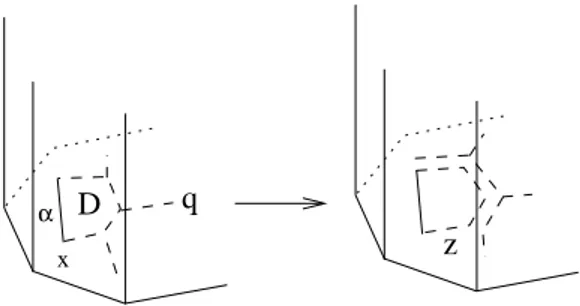
Figura 1.1: Una compressione.

La stessa operazione si chiama anche chirurgia lungo D, e D si dice disco di

compressione.

Se S è una superficie propriamente embedded in una 3-varietà M e ∆ è una famiglia di dischi propriamente embedded in M \ S, indicheremo con S∆ oppure

con σ(S; ∆) la superficie (magari sconnessa) ottenuta da Σ comprimendo lungo ∆.

Definizione 1.11. Una famiglia ∆ di dischi di compressione per una superficie

S si dice massimale se valgono le tre propriet`a seguenti. 1. σ(S; ∆) `e incompressibile;

2. i dischi appartenenti a ∆ sono a due a due non paralleli;

3. per ogni famiglia ∆0 _{! ∆ di dischi di compressione per S tale che σ(S; ∆}0₎

sia incompressibile la condizione 2 non `e verificata.

Definizione 1.12. Una superficie S propriamente embedded in una 3-variet`a M

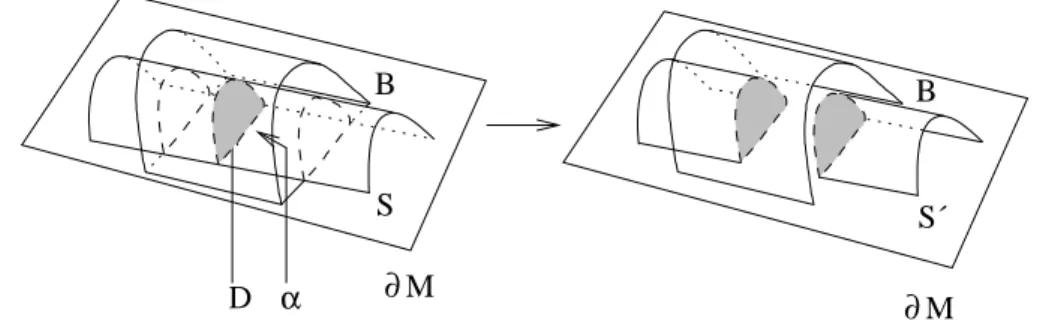
si dice ∂-compressibile se esiste un disco D ⊂ M con α = D ∩ S ∂D arco essenziale in S e ∂D \ α ⊂ ∂M .

Altrimenti, diremo che S `e ∂-incompressibile. Il disco D si dice disco di ∂-compressione.

Definizione 1.13. Sia S una superficie propriamente embedded in una 3-variet`a

M , e sia D un disco propriamente embedded in M \ S con α = D ∩ S ∂D. Una ∂-compressione lungo α `e la seguente operazione. Sia

B = ¯η(D) ∼= {z ∈ D2| Re(z) ≥ 0} × [−1, 1], in modo che D = {z ∈ D2| Re(z) ≥ 0 e kzk ≤ 1/2} × {0} e

(8)

Alla superficie S sostituiamo la superficie S0 _{tale che} S0∩ (M \ B) = S ∩ (M \ B) e S0∩ B = α × ([−1, −1/2] ∪ [1/2, 1]) ∪ ({z ∈ D2| Re(z) ≥ 0} × {−1/2, 1/2}). ∂M ∂M S B _B S´ D α

Figura 1.2: Una ∂-compressione.

La stessa operazione si chiama anche ∂-chirurgia lungo D.

1.2.2 Superfici planari e gerarchie

Definizione 1.14. Una superficie si dice planare se ogni sua componente

con-nessa ha bordo ed `e di genere 0.

Definizione 1.15. Una gerarchia per una superficie T `e una successione di coppie (T0, α0), ..., (Tn, αn) dove T0 = T , gli αi sono archi o curve semplici essenziali in

Ti, la superficie Ti+1 `e ottenuta da Ti tagliando lungo αi ed ogni componente

connessa di Tn+1 `e un disco.

Il seguente lemma si dimostra facilmente per induzione.

Lemma 1.16. Sia T una superficie planare con z componenti connesse che non

siano dischi e b componenti connesse di bordo. Sia (T₀, α₀), ..., (T_n, α_n) una

gerar-chia per T dove tutti gli αi siano archi. Se Tn+1 ha d componenti connesse, allora

d ≤ b − z.

(9)

1.3 Manici

Definizione 1.17. Sia data una 3-variet`a orientabile M , e fissiamo un intero 0 ≤ i ≤ 3. Se i = 3 scegliamo una sfera C ⊂ ∂M , se i = 2 scegliamo una

curva semplice chiusa C ⊂ ∂M , se i = 1 scegliamo due punti distinti p, q ∈ ∂M e poniamo C = {p, q}, se i = 0 scegliamo C = ∅ ⊂ ∂M . Consideriamo una mappa

f : D3−i× ∂Di−→ ∂M

che sia un diffeomorfismo con l’immagine, mantenga l’orientazione e sia tale che f ({0} × ∂Di_{) = C. La 3-variet`a}

M0 = M t (D3−i× Di)

∼ ,

dove ∼ `e la relazione di equivalenza indotta da f , si dice ottenuta da M mediante

attaccamento di un i manico lungo C. Il cuore di tale i-manico `e {0} × Di _{⊂ M}0_,

mentre D3−i_{× {0} ⊂ M}0 _{si dice cocuore del manico.}

Tutte le funzioni di Morse che utilizzeremo nel corso della tesi saranno tali che ad ogni valore critico corrisponder`a un solo punto critico.

Teorema 1.18. Data una 3-variet`a M ed una funzione di Morse f : M → [0, 1],

sia a un livello critico di indice i di f . Allora esiste ε > 0 tale che il sottolivel-lo f−1_{([0, a + ε]) si ottiene mediante attaccamento di un i-manico al sottolivello}

f−1_{([0, a − ε]).}

Dimostrazione. Si deriva dal Teorema 3.2 di [Mi2].

1.4 Variet`

a prodotto F × I

Teorema 1.19. Sia M una 3-variet`a compatta tale che nessuna componente

con-nessa di ∂M sia una sfera, e F ⊂ ∂M una superficie tale che i_∗ : π₁(F ) → π₁(M )

sia un isomorfismo. Allora M `e omeomorfa a F × I mediante un omeomorfismo che porta F su F × {0}.

Dimostrazione. [H], Teorema 10.2, adattato al caso in cui ∂F non contiene sfere.

Definizione 1.20. Una superficie S propriamente embedded in F × S1 _{si dice}

verticale in q ∈ S se p_∗ : T_qS → T_p(q)F è singolare. Se S è verticale in q per ogni q ∈ S, diciamo che S è verticale. Diciamo invece che S è orizzontale se non è verticale in nessun punto, e che è strettamente orizzontale se p0

∗ : TqS → Tp0_(q)S1 `e singolare.

(10)

Enunciamo il seguente risultato, che sar`a dimostrato nel Capitolo 3.

Lemma 3.25. Sia S ⊂ F × S1 _{una superficie compatta. Se S `e} incompressi-bile, esiste un’isotopia che la porta in una superficie verticale oppure orizzontale. Equivalentemente, esiste un’isotopia dopo la quale S diventa una unione di tori verticali oppure p|S : S → F `e un rivestimento.

Il lemma seguente si dimostra utilizzando il Lemma 3.25.

Lemma 1.21. Sia F 6= S2 _{una superficie orientabile compatta chiusa, e S una} superficie incompressibile in F × I. Allora S `e parallela a F × {0}.

1.5 Posizione magra

Definizione 1.22. Sia M una 3-variet`a, e sia data una funzione f : M → [0, 1].

Se C ⊂ ∂M , diremo che f è di Morse modulo C se è di Morse su M \ C, ed esiste un collare ¯η(C) ∼= C × I tale che f è costante sulle componenti connesse di

C × {t} per ogni t ∈ I.

In questa sezione M sarà una 3-varietà compatta e f : M → [0, 1] una funzione di Morse modulo ∂M fissata. Sia k : X → M un nodo, cioè un embedding proprio di una varietà X ∈ {I, S1_{} in M .}

Definizione 1.23. Il nodo k `e in posizione generica rispetto a f se f ◦ k `e di

Morse modulo ∂X, e i valori critici di f ◦ k sono distinti da quelli di f .

Dopo aver messo k in posizione generica rispetto a f con un’isotopia, siano

x1 < ... < xn i valori critici di f ◦ k, e siano a0, ..., an valori regolari di f ◦ k tali

che 0 < a0 < x1 e xn< an < 1, e tali che xi < ai< xi+1 per i = 1, ..., n − 1. Per

a ∈ [0, 1] poniamo Fa= f−1(a).

Definizione 1.24. L’ ampiezza del nodo k `e il numero

w(k) =

n

X

i=0

|Fai∩ k(X)|.

Diremo che k `e in posizione magra se minimizza w(k) all’interno della sua classe di isotopia. Diremo invece che k `e in posizione magra modulo ∂k se minimizza w(k) all’interno della sua classe di isotopia modulo ∂k.

Dato un link L : (X₁, ..., X_n) → M (dove X_i∈ {I, S1_{}), diremo che esso `e in}

posizione magra se minimizza la sua ampiezza

w(L) =

n

X

i=0

|Fai∩ L(X1, ..., Xn)|

(11)

Spesso confonderemo un nodo k o un link L con le rispettive immagini k(X) e L(X₁, ..., X_n).

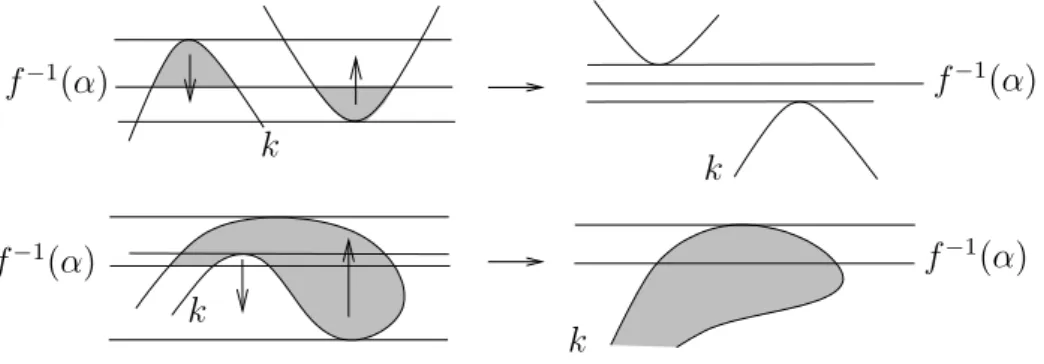
Sia α ∈ [0, 1], e λ un sottoarco di k tale che ∂λ ⊂ f−1_{(α) ed esista un disco}

D tale che ∂D ⊂ λ ∪ f−1_{(α) e D ∩ k = λ; se esiste un intorno η(λ) di λ tale che}

D ∩ η(λ) ⊂ f−1([0, α]) diciamo che D è un disco alto, λ è un arco alto e α è un

livello basso, mentre se D ∩ η(λ) ⊂ f−1_{([α, 1]) diremo che D `e un disco basso, λ `e}

un arco basso e α è un livello alto. Abbiamo il seguente importante lemma. Lemma 1.25. Se M è una 3-varietà con una funzione di Morse f : M → [0, 1], e

k `e in posizione magra rispetto a f , nessun livello pu`o essere contemporaneamente alto e basso.

Dimostrazione. Se esistesse un livello contemporaneamente alto e basso,

trove-remmo un’isotopia che farebbe diminuire l’ampiezza di k (Figura 1.3).

k k k k f−1_(α) f−1_(α) f−1_(α) f−1_(α)

(12)

Capitolo 2

Spezzamenti di Heegaard di

3-variet`

a

In questo capitolo saranno definiti gli spezzamenti di Heegaard per una terna (M, ∂1M, ∂2M ), e saranno caratterizzati gli spezzamenti delle variet`a F × I, con F 6= S2 _{superficie compatta chiusa.}

2.1 Compression body

Definizione 2.1. Sia F una superficie compatta chiusa di genere g. Incolliamo dei 2-manici su F × {0} ⊂ F × I, e tappiamo con dei 3-manici eventuali sfere venutesi

a creare nel bordo della variet`a risultante. La 3-variet`a W cos`ı ottenuta si chiama

compression body di genere g. Si pone ∂₊W = F × {1}, e ∂₋W = ∂W \ ∂₊W . Un handlebody `e un compression body W con ∂−W = ∅.

Definizione 2.2. Un compression body pu`o essere ottenuto anche nel seguente

modo: siano s, n ≥ 0; per j = 1, ..., s sia Bj una copia della palla B3, e per

i = 1, ..., n sia Gi una superficie di genere gi. Su n [ i=1 (Gi× {1}) t s [ j=1 ∂Bj ⊂ n [ i=1 (Gi× [0, 1]) t s [ j=1 Bj

si attaccano 1-manici in modo da ottenere una varietà connessa. Il risultato è un compression body di genere g+k−s−n+1, dove k è il numero di 1-manici utilizzati nella costruzione e g = Pn_i=1gi. In questo caso si ha ∂−W =

S_n

i=1Gi × {0} e

∂+W = ∂W \ ∂−W .

Osservazione 2.3. La decomposizione in manici di un compression body W non è unica; si può sempre utilizzare al più un 3-manico, e non utilizzarne affatto nel caso in cui W non sia un handlebody.

Sia D il cuore di un 2-manico usato per costruire un compression body W ; allora γ = ∂D ⊂ F × {0}, e γ borda un disco D in M . Pertanto possiamo dare la seguente definizione.

(13)

Definizione 2.4. Data una decomposizione in manici di W , l’insieme dei dischi

{(γ × [0, 1]) ∪ D}, o un insieme di dischi ad esso isotopo, si dice sistema completo

di dischi per W .

Definizione 2.5. Un sistema completo di dischi relativo ad una decomposizione

in manici si dice minimale se non contiene propriamente nessun altro sistema completo di dischi (al variare della decomposizione in manici).

Osservazione 2.6. Tagliando un compression body lungo un sistema completo di dischi minimale si ottiene una variet`a omeomorfa a F × I, dove F `e una superficie, magari sconnessa.

Lemma 2.7. Sia W un compression body, e ∆ una famiglia di dischi propriamente

embedded in W . La 3-variet`a W0 _{ottenuta tagliando lungo ∆ `e una unione di}

compression body, e ∂−W0∼= ∂−W .

Dimostrazione. Ragionando per induzione, possiamo supporre che ∆ consista di

un solo disco. Scegliamo un sistema completo di dischi minimale Θ per W , tale che il numero di componenti connesse di Θ ∩ ∆ sia il minimo possibile. Vogliamo dimostrare che Θ ∩ ∆ = ∅.

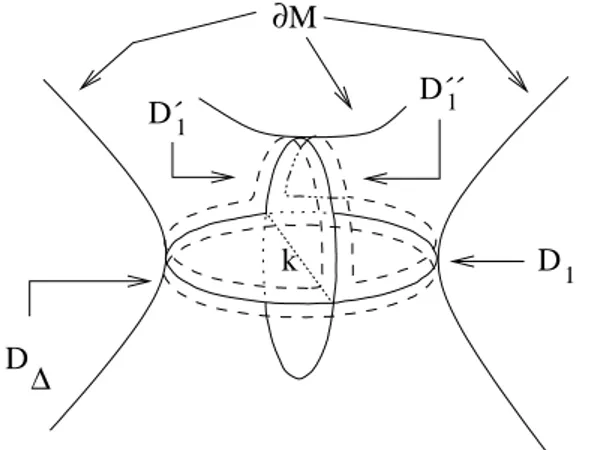
Se esiste una componente connessa di Θ ∩ ∆ costituita da una curva semplice chiusa α, essa borda un disco sia in Θ che in ∆. Poich´e W `e irriducibile, possiamo eliminare α con un’isotopia.

D´´₁ D´₁

∂M

D_∆

k D₁

Figura 2.1: Il disco D∆ e i dischi D10 e D100.

Se esiste una componente connessa di Θ ∩ ∆ costituita da un arco, sia k una di tali componenti connesse tale che uno dei dischi componenti ∆ \ k non intersechi Θ. Indichiamo con D∆ tale disco, e con D1 il disco di Θ contenente k (Figura

2.1). Poniamo U = ¯η(D1∪ D∆); allora ∂U `e formato da tre componenti connesse,

delle quali una `e un disco parallelo a D1. Indichiamo con D10 e D100 le altre. Allora

il numero di componenti connesse dell’intersezione di Θ0 = (Θ \ D1) ∪ D10 ∪ D001 con

(14)

da W \ Θ0 _{attaccando un 1-manico, pertanto Θ}0 _{`e ancora un sistema completo di}

dischi minimale per W , assurdo.

Allora ∆ ⊂ W \ Θ ∼= F × I, pertanto una delle componenti connesse di (W \ Θ) \ ∆ è una sfera, e l’altra è un compression body omeomorfo a W \ Θ. Riattaccando degli 1-manici a (W \ Θ) \ ∆ utilizzando le curve componenti ∂Θ come cocuori, si ricostruisce W \ ∆, pertanto W \ ∆ è un compression body W0. Inoltre, se ∆ ∩ ∂−(W \ Θ) = ∅ vale ∂−W0= ∂−W ; se invece ∆ ∩ ∂−(W \ Θ) = ∂∆,

una delle sfere componenti (W \ Θ) \ ∆ descrive un parallelismo fra ∆ ed un disco contenuto in ∂−W0, pertanto ∂−W0∼= ∂−W .

Osservazione 2.8. Se ∆ `e una famiglia di dischi essenziali in un compression body

W a due a due non paralleli, esiste un sistema completo di dischi che contiene ∆.

Infatti, M \ ∆ `e una unione di compression body W1∪ ... ∪ Wk per il Lemma 2.7,

e nessuno di essi è una palla perché i dischi di ∆ non sono paralleli fra loro né a dischi contenuti in ∂W. Allora basta scegliere sistemi completi di dischi minimal

∆i per Wi, per i = 1, ..., k, e porre ∆0 = ∆ ∪ ∆1∪ ... ∪ ∆k.

Definizione 2.9. Un anello A propriamente embedded in un compression body

W si dice quasi verticale se una delle componenti connesse di ∂A `e contenuta in ∂₋W e l’altra in ∂₊W .

Definizione 2.10. Un arco γ propriamente embedded in un compression body W

si dice quasi verticale se uno degli estremi di γ `e contenuto in ∂₋W e l’altro in ∂+W .

Lemma 2.11. Sia W un compression body con ∂−W 6= ∅, e S una famiglia di

anelli quasi verticali essenziali disgiunti. Allora esistono un sistema completo di dischi ∆ tale che ∆ ∩ S = ∅ e W \ ∆ ∼= ∂−W × I, ed una funzione di Morse

f : W → [0, 1] avente punti critici di indice 1 solamente tale che ∂−W = f−1(0)

e ∂+W = f−1(1), e tale che le linee di flusso del gradiente di f uscenti dai punti critici non intercano S.

Dimostrazione. L’esistenza di ∆ si ottiene ripetendo il ragionamento utilizzato nel

Lemma 2.7 per mostrare che Θ ∩ ∆ = ∅.

Grazie al Lemma 2.36, dimostrato in maniera indipendente nel seguito, con un’isotopia S diventa una famiglia di anelli verticali. Allora basta scegliere come

f la funzione di Morse indotta dall’attaccamento di 2-manici lungo ∆.

2.1.1 Spine di compression body

Con la seguente definizione introduciamo il concetto di spina secondo la nozione che ne viene data in [ST].

Definizione 2.12. Un grafo G propriamente embedded in un compression body

(15)

a´ a c p b d _p b´ d

Figura 2.2: Uno slittamento.

Data una spina Q per un compression body W , scegliamo due lati distinti a e

b aventi un vertice c in comune, e sia ∂b = c ∪ d. Scegliamo un punto p ∈ a; detto a0 _{l’arco contenuto in a avente c e p come estremi, sia b}0 _{un arco avente estremi in}

d e p isotopo a b ∪ a0_.

Definizione 2.13. La spina ottenuta sostituendo l’arco b con l’arco b0 si dice costruita per slittamento da Q.

Analogamente, dati due lati a e b di Q, con a1 = a ∩ ∂−W = ∂a ∩ ∂−W e

b1 = b ∩ ∂−W = ∂b ∩ ∂−W , scegliamo un arco β ⊂ ∂−W avente a1 e b1 come

estremi e due punti a2 ∈ a e b2∈ b; indicati con a0 il sottoarco di a avente a1 e a2

come estremi e b0 l’arco contenuto in b e avente b1 e b2 come estremi, scegliamo

un arco ˜β avente a2 e b2 come estremi e isotopo a b ∪ β ∪ a0.

a 1 b 1 b 2 β ~ a 2 a2 ~ β b 2 β a´ b´ a b _a b a´

Figura 2.3: Uno slittamento.

Definizione 2.14. La spina ottenuta sostituendo l’arco b con l’arco (b \ b0_{) ∪ ˜}_{β si}

dice costruita per slittamento da Q.

Osservazione 2.15. La costruzione di un compression body mediante attacca-mento di 1-manici fornisce una funzione di Morse f : W → I tale che f−1_(1)=∂

+W

e f−1_{(0) = ∂}

−W (se ∂−W 6= ∅) oppure f−1(0) `e un minimo (se W `e un

handle-body). Detto ∆ il sistema completo di dischi corrispondente ad una famiglia di 2-manici che costruiscono W , diremo che f `e definita da ∆.

Lemma 2.16. Sia W un compression body con ∂−W 6= ∅, e f una funzione di

Morse definita da un sistema completo di dischi minimale. Sia δ una famiglia finita di curve chiuse semplici disgiunte contenute in ∂−W , e Γ una famiglia

(16)

e (Γ ∩ ∂−W ) ∩ δ = ∅. Allora esiste una famiglia ∆ ottenuta aggiungendo ad un

sistema completo di dischi per W una famiglia Ξ di anelli quasi verticali tali che

Ξ ∩ ∂−W = δ e Γ ∩ ∆ = ∅. Inoltre, gli archi appartenenti a Γ sono isotopi ad

archi verticali nella variet`a W \ η(∆) ∼= (∂−W \ η(δ)) × I.

Dimostrazione. Sia n il numero di punti critici di f , e ragioniamo per induzione

(17)

Consideriamo il caso in cui f non abbia punti critici. Allora W `e un prodotto

∂₋W × I, e Γ `e composto di archi quasi verticali; utilizzando flusso del gradiente

di f |Γ possiamo costruire un’isotopia F : ∂−W × I → W tale che:

• F (p, 0) = p per ogni p ∈ ∂₋W ; • F (p, 1) ∈ ∂+W per ogni p ∈ ∂−W ;

• F (p, t) ∈ Γ per ogni p ∈ Γ ∩ ∂−W .

Allora possiamo prendere ∆ = F (δ × I); in questo caso ∆ `e formato soltanto da anelli quasi verticali.

Sia ora n > 0, e sia a₁ il minimo valore critico di f ; con una isotopia rendiamo Γ trasversale a f−1_{([0, a}

1]). Allora possiamo applicare il ragionamento appena

svolto al compression body f−1_{([0, a}

1−ε]) per ε > 0 sufficientemente piccolo, con la

famiglia di curve δ e gli archi Γ∩f−1_{([0, a}

1−ε]), ed otteniamo una famiglia di anelli

quasi verticali in f−1([0, a1− ε]). Per il Lemma 1.18 il sottolivello f−1([0, a1+ ε])

si ottiene attaccando un 1-manico al sottolivello f−1_{([0, a}

1− ε] se ε `e abbastanza

piccolo, e possiamo far s`ı che i dischi sui quali tale 1-manico viene attaccato siano disgiunti da Γ ∩ f−1(a1− ε) e da δ1 = ∆ ∩ f−1(a1). Allora possiamo completare

∆ nel compression body f−1_{([0, a}

1+ ε]) aggiungendovi il cocuore dell’1-manico

attaccato. Applicando l’ipotesi induttiva al compression body f−1_([a

1+ ε, 1]) con

la famiglia di curve δ1∪ ∂D e la famiglia di archi Γ ∩ f−1([0, a1− ε]) si conclude

la dimostrazione.

In maniera analoga possiamo dimostrare il seguente lemma.

Lemma 2.17. Sia W un compression body tale che ∂₋W 6= ∅, e f una funzione di Morse su W definita da un sistema completo minimale di dischi per W . Sia Γ una famiglia di archi propriamente embedded in W tale che f |Γ non abbia punti critici. Allora esiste una spina Q di W con Q ∩ Γ = ∅ tale che Γ `e formato da archi isotopi ad archi verticali in W \ η(Q) ∼= ∂+W × I.

2.2 Spezzamenti di Heegaard

Data una 3-variet`a M , sia ∂M = ∂1M t ∂2M , dove ∂iM `e unione di componenti

connesse di ∂M (non stiamo richiedendo ∂iM 6= ∅).

Definizione 2.18. Uno spezzamento di Heegaard di una terna (M, ∂1M, ∂2M ) `e una coppia (W1, W2) di compression body tali che ∂−Wi = ∂iM per i = 1, 2, con

W1∪ W2 = M e W1∩ W2 = ∂+W1= ∂+W2. La superficie Σ = W1∩ W2 si chiama

superficie di Heegaard. Il genere di tale spezzamento di Heegaard `e il genere di Σ. Osserviamo che se ∂M non contiene sfere ogni terna (M, ∂1M, ∂2M ) ammette

uno spezzamento di Heegaard. Infatti, sia T una triangolazione di M tale che ogni simplesso sia incidente al pi`u ad una componente connessa di ∂M . Sia T0

(18)

la suddivisione baricentrica, e eT il grafo duale di T ; la parte interna dei simplessi

di T0 _{incidenti a ∂}

2M `e un collare di ∂2M , pertanto rimuovendola si ottiene una

variet`a M0 omeomorfa a M . Chiamiamo ∂₂0M la componente di bordo di M0

corrispondente a ∂2M . Sia Γ1 l’unione di ∂1M e di tutti i vertici ed i lati di T che

non intersecano ∂2M , e Γ2 l’unione di ∂20M e di tutti i vertici e i lati di eT ∩ M0

che non intersecano Γ1. Allora gli intorni regolari di Γ1 e Γ2 d`anno i compression

body W1 e W2 cercati, e Γi `e una spina di Wi (Figura 2.4).

Γ1 T T0 Γ2 T T0 e T ∂0 2M ∂2M ∂1M ∂1M ∂0 2M ∂2M Figura 2.4: I grafi Γ1 e Γ2.

Nel seguito commetteremo l’abuso di notazione di scrivere “spezzamento di Heegaard di una variet`a M ” senza fare riferimento ad una terna (M, ∂1M, ∂2M );

con questo intenderemo riferirci ad uno spezzamento di Heegaard di una qualsiasi terna (M, ∂1M, ∂2M ).

Inoltre confonderemo uno spezzamento di Heegaard con la relativa superficie di Heegaard: ciò è lecito data la corrispondenza fra i due concetti. Due spezzamenti di Heegaard di una 3-varietà saranno considerati uguali se le rispettive superfici sono isotope.

Dato uno spezzamento di Heegaard (W₁, W₂) di una 3-variet`a M , fissiamo per

W1, per i = 1, 2, un sistema completo di dischi minimale, e siano fi : Wi → I le

funzioni considerate nell’Osservazione 2.15. Se incollando fra loro W1 e W2 per

ottenere M incolliamo fra loro anche le funzioni f_i, otteniamo una funzione di Morse h : M → [0, 1] con valori critici

(19)

tali che: 1. h−1_(a

i) contiene un punto critico di indice 1;

2. h−1(bj) contiene un punto critico di indice 2;

3. h−1_{(0) = ∂}

1M se ∂1M 6= ∅, altrimenti contiene un punto critico di indice 0;

4. h−1_{(1) = ∂}

2M se ∂2M 6= ∅, altrimenti contiene un punto critico di indice 3;

5. per ak< t < b1 vale h−1(t) ∼= Σ.

Nel seguito diremo che una tale h definisce lo spezzamento di Heegaard.

2.2.1 Stabilizzazione e riducibilit`a

Sia (W₁, W₂) uno spezzamento di Heegaard di una 3-variet`a M . Sia α un arco propriamente embedded in W2 con estremi in Σ e parallelo ad un arco in Σ.

Poniamo W0

1 = W1 ∪ ¯η(α) e W20 = W2 \ η(α). Allora (W10, W20) `e ancora uno

spezzamento di Heegaard di M ; il suo genere `e di uno pi`u grande di quello di (W1, W2).

Definizione 2.19. Lo spezzamento di Heegaard (W0

1, W20) cos`ı ottenuto si dice

stabilizzazione di (W1, W2). Lo spezzamento (W1, W2) si dice destabilizzazione di

(W0

1, W20).

Lemma 2.20. Uno spezzamento di Heegaard (W1, W2) `e stabilizzato se e solo se esistono dischi Di ⊂ Wi per i = 1, 2 propriamente embedded e trasversali fra loro

con |∂D_i∩ ∂D₂| = 1.

Dimostrazione. [Scha], Lemma 3.1.

Date due 3-variet`a M e M0_{con spezzamenti di Heegaard (W}

1, W2) e (W10, W20),

siano B e B0_{due 3-palle intersecanti rispettivamente Σ e Σ}0 _{in dischi equatoriali D}

e D0; allora la superficie Σ#Σ0 ottenuta identificando Σ ∩ ∂D con Σ0∩ ∂D0 d`a uno spezzamento di Heegaard della 3-variet`a M #M0 _{ottenuta identificando ∂B ⊂ M}

con ∂B0_{⊂ M}0 _{e ∂D con ∂D}0_{. Viceversa, se esistono dischi essenziali D}

i⊂ Wi

pro-priamente embedded con ∂D1 = ∂D2 ⊂ Σ lo spezzamento di Heegaard (W1, W2)

di M pu`o essere costruito col procedimento appena descritto. Questo motiva la seguente definizione.

Definizione 2.21. Uno spezzamento di Heegaard (W1, W2) si dice riducibile se esiste una 2-sfera in M che interseca Σ in un unico cerchio essenziale.

Lemma 2.22. Sia Q una spina di un compression body definito da uno

spezza-mento di Heegaard di una 3-varietà M 6= S3_{. Se un ciclo di Q è contenuto in una} palla, lo spezzamento di Heegaard è riducibile.

(20)

Dimostrazione. Sia W il compression body del quale Q `e una spina, e γ ⊂ Q un

ciclo contenuto in una palla B ⊂ M . Sia U un intorno tubolare di γ in W . Allora

Q ∩ (W \ U ) `e una spina per W \ U ), che pertanto `e un compression body, e

Σ = ∂+W è una superficie di Heegaard per M \ U . Questa varietà è riducibile,

perché ∂B non borda una palla (perché M 6= S3_{). Pertanto Σ è riducibile, ed è}

riducibile anche in M .

Abbiamo il seguente teorema, dimostrato in [W].

Teorema 2.23. Ogni spezzamento di Heegaard di genere positivo di S3 _`e stabi-lizzato.

Grazie al Teorema 2.23 per ogni g ≥ 0 esiste un unico spezzamento di Heegaard di S3 di genere g.

Proposizione 2.24. Ogni spezzamento di Heegaard stabilizzato diverso da quello

di genere 1 di S3 `e riducibile.

Dimostrazione. Siano D_i ⊂ W_iper i = 1, 2 dischi fra loro trasversali tali che valga

|∂D1∩ ∂D2| = 1; sia Bi un bicollare di Di in Wi. Sia B = B1∪ B2; questa `e una

palla, e B ∩ Σ è una superficie omeomorfa ad un toro meno un disco. Se ∂S ∩ Σ è essenziale in Σ, allora ∂B è una sfera che riduce lo spezzamento di Heegaard.

Se invece ∂B ∩ Σ `e inessenziale in Σ, allora Σ = (B ∩ Σ) ∪ ((M \ B) ∩ Σ) `e un toro; inoltre i meridiani dei tori solidi in cui viene divisa M si intersecano in un solo punto, quindi M = S3_.

Con il Teorema 2.23 si dimostra la seguente proposizione, che inverte la pre-cedente nel caso delle variet`a irriducibili.

Proposizione 2.25. Sia M una variet`a irriducibile. Allora ogni spezzamento di

Heegaard riducibile `e stabilizzato.

Dimostrazione. Sia S una sfera tale che α = S ∩ Σ è essenziale in Σ. Poiché M è

irriducibile, S borda una palla aperta B; l’intersezione Σ ∩ B `e omeomorfa ad una superficie compatta alla quale `e stato tolto un punto. Tappando questa superficie con un disco e poi collassando ∂B ⊂ B ad un punto otteniamo uno spezzamento di Heegaard di S3. Tale spezzamento di Heegaard ha genere positivo in quanto

α `e essenziale in Σ. Esso `e stabilizzato per il Teorema 2.23, quindi ci sono dischi

trasversali D_i ⊂ S3 _{per i = 1, 2, uno in ogni componente connessa di S}3 _{\ Σ,}

con |∂D1∩ ∂D2| = 1; queste propriet`a sono mantenute anche in M , quindi Σ `e

(21)

Teorema 2.26. Sia M una 3-variet`a riducibile, e (W1, W2) un suo spezzamento di Heegaard. Allora (W₁, W₂) `e riducibile.

Dimostrazione. Fra tutte le sfere incompressibili scegliamone una, che chiamiamo S, che intersechi Σ trasversalmente e minimizzi il numero di componenti connesse

di tale intersezione. Poiché un compression body è irriducibile e S è incompressi-bile, S non può essere contenuta interamente in W1 né in W2, pertanto S ∩ Σ 6= ∅.

Per una tale S necessariamente S ∩ W₁ `e incompressibile in W₁ e W₂ rispetti-vamente. Infatti, supponiamo per assurdo che esista un disco di compressione

D ⊂ W1: operando una chirurgia di S lungo D si ottengono due sfere S1 e S2; se

esse bordassero palle B₁ e B₂, anche S borderebbe una palla ottenuta da B₁∪ B₂

con attaccato un 1-manico, assurdo.

Quindi possiamo supporre che S1 sia incompressibile. Allora, poich´e D `e tale

che [∂D] 6= 0 in π₁(S ∩ W₁), la sfera S₁ `e una sfera incompressibile tale che S₁∩ Σ

`e formato da meno componenti connesse di S ∩ Σ, contro la scelta di S.

Dico che S∩W1 e S∩W2sono dischi, il che basta a concludere la dimostrazione.

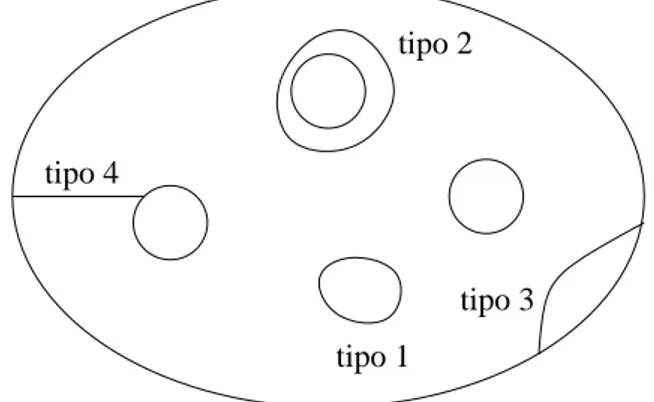
Supponiamo per assurdo che una componente connessa di S ∩ W₁ non sia un disco. Supponiamo anche per ora che W1 sia un handlebody, e scegliamo un

sistema completo di dischi ∆ per W1 trasversale a S ∩ W1.

Sia D ∈ ∆, e consideriamo ∆ ∩ (S ∩ W1) ⊂ S ∩ W1; le sue componenti connesse

possono essere di quattro tipi (Figura 2.5).

tipo 1 tipo 2

tipo 3 tipo 4

Figura 2.5: I quattro tipi di archi e curve possibili.

Caso 1: se ∆ ∩ (S ∩ W1) contiene delle curve chiuse inessenziali, sia α una

tale curva, scelta in modo che una componente connessa di ∆ ∩ (S ∩ W1) \ α

non intersechi ∆ ∩ (S ∩ W₁), e sia D il disco di ∆ che contiene α. Poiché α borda un disco in D, e poiché W1 è incompressibile, possiamo fare un’isotopia di D che elimina α dalle componenti connesse di ∆ ∩ (S ∩ W1). Ripetiamo questo

procedimento fino ad eliminare tutte le curve chiuse inessenziali.

Caso 2: se ∆ ∩ (S ∩ W1) contiene una curva chiusa essenziale, scegliamone una,

(22)

∆, e sia D il disco di ∆ che contiene α. Allora α borda un disco in D, contro l’incompressibilit`a di S ∩ W₁. Quindi S ∩ W₁ non interseca ∆ in curve chiuse essenziali.

Caso 3: se ∆ ∩ (S ∩ W1) contiene un arco α inessenziale, siano D il disco di ∆

che contiene α e D0 _{il disco di S ∩ W}

1 che descrive il parallelismo di α con un arco γ di ∂(S ∩ W1); possiamo scegliere α in modo che D0∩ ∆ = ∅. Chiamiamo D1 e D2 i dischi in cui α divide D. Uno di questi due dischi, ad esempio D1, è tale che D1∪D0è un disco inessenziale in W1. Poiché W1è incompressibile, ∂D1∪D0 borda

un disco D00 in ∂W1; poich´e W1 `e irriducibile, la sfera D1 ∪ D0 ∪ D00 borda una

palla B, che possiamo utilizzare per fare un’isotopia che elimini α da ∆∩(S ∩W1).

Ripetiamo questa operazione fino ad eliminare tutti gli archi inessenziali.

Caso 4: ci siamo quindi ridotti al caso in cui ∆ ∩ (S ∩ W1) sia formato solo da

archi αi, per i = 1, ..., n+1, essenziali in S ∩W1e paralleli a degli archi βi⊂ ∂+W1.

Supponiamo per ora che l’arco αj non sia parallelo all’arco αk se j 6= k in

S ∩ W1; allora, posto (S ∩ W1)0 = S ∩ W1, l’arco αi+1`e essenziale nella superficie

(S ∩ W1)i = (S ∩ W1)i−1\ αi, per i = 0, ..., n. Allora gli archi αi d`anno luogo a

una gerarchia per S ∩ W1. Infatti, se una componente connessa A di (S ∩ W1)n+1

non fosse un disco, sarebbe π₁(A) 6= 0, ma A ⊂ W₁\S_iα_i ∼= B3, pertanto A non sarebbe incompressibile, contro l’incompressibilit`a di S ∩ W1.

Allora pratichiamo ∂-chirurgie in W1lungo i dischi bordati da αi∪βiottenendo

una sfera S0 _{isotopa a S e trasversale a Σ tale che ogni componente connessa di}

S0_{∩ W}

1 `e un disco. Sia b il numero di componenti connesse di S ∩ Σ = ∂(S ∩ W1).

Sia d il numero di componenti connesse di S0_{∩Σ = ∂(S ∩W}

1)n+1. Se z `e il numero

di componenti connesse di S ∩ W₁ che non sono dischi, per il Lemma 1.16 vale

d ≤ b−z. Allora mediante una piccola isotopia S0_{diventa una sfera incompressibile}

che interseca Σ trasversalmente e le componenti connesse di S0_{∩ Σ sono meno di}

quelle di S ∩ Σ, assurdo.

Se invece gli archi αi non sono a due a due non paralleli, `e sufficiente, al

momento del taglio lungo l’arco αj, eliminare dalla lista degli αi tutti gli archi αk,

con k > j, paralleli a α_j, e concludere come nel caso precedente.

Nel caso in cui W1non sia un handlebody, possiamo tappare le componenti

con-nesse di ∂−W1 con 2-manici e 3-manici fino ad ottenere un handlebody W10 ⊃ W1.

Poi applichiamo il ragionamento svolto a W0

1 avendo cura che tutte le isotopie del

sistema completo di dischi mantengano sempre W1 in s´e e W10\ W1 in s´e.

Definizione 2.27. Uno spezzamento di Heegaard (W₁, W₂) di una 3-variet`a M

si dice debolmente riducibile se esistono dischi Di ⊂ Wi con ∂D1 ∩ ∂D2 = ∅. Altrimenti, (W1, W2) si dice fortemente irriducibile.

Abbiamo un risultato analogo al Teorema 2.26 per le varietà ∂-riducibili. Teorema 2.28. Sia M una 3-varietà ∂-riducibile, e (W1, W2) un suo spezzamento di Heegaard tale che Wi sia non banale per i = 1, 2. Allora (W1, W2) è debolmente riducibile.

(23)

Lemma 2.29. Sia Σ una superficie di Heegaard per una 3-varietà M , e (W1, W2) lo spezzamento di Heegaard risultante. Sia T ⊂ Σ una superficie compatta con bordo tale che ogni componente connessa di ∂T sia essenziale in Σ, e supponiamo che ogni componente connessa di ∂T bordi un disco in M disgiunto da T . Allora◦ o la famiglia di dischi bordata da ∂T è contenuta in un singolo compression body Wi, oppure Σ è debolmente riducibile.

Dimostrazione. Chiamiamo N la 3-variet`a ottenuta da M rimuovendo una copia

di T × [−1, 1] in modo che T ∼= T × {0}, e sia S = Σ ∩ N , con ∂S = ∂T . Poich´e ogni componente connessa di ∂T borda un disco in M ma non in Σ, la superficie

S `e compressibile in N . Supponiamo che S possa venire compressa in W2, e sia ∆

una famiglia massimale di dischi di compressione per S ⊂ W2. Se S0 = σ(S; ∆) `e

incompressibile in N , allora ∂S0 _{= ∂T `e inessenziale in S}0_{e ∂T borda una famiglia}

di dischi interamente contenuta in W2.

Se invece S0 _{`e compressibile in N , deve poter venire compressa nella}

compo-nente connessa N0 _{di N \ S contenente W}

1. Scegliamo una curva semplice chiusa c

essenziale in S0 che bordi un disco in N0. Tale curva `e contenuta anche in S ⊂ Σ, in quanto S si ottiene da S0 _{attaccando 1-manici fuori da un intorno di c. Essa}

inoltre `e essenziale in Σ: se c bordasse un disco in Σ, tale disco rimarrebbe dopo le compressioni anche in S e in S0.

Per lo stesso motivo, ogni componente connessa di ∂∆ `e essenziale in Σ, e Σ d`a uno spezzamento di Heegaard non banale di N0_{. Inoltre le componenti connesse}

di N0\ Σ sono W1 ed un compression body ottenibile attaccando 2-manici a Σ

lungo ∂∆. Poiché c borda un disco in N0_{, la varietà N}0 _{è ∂-riducibile, pertanto}

per il Teorema 2.28 Σ `e debolmente riducibile.

2.2.2 Amalgamazione

Siano M1, M2 due 3-variet`a con bordo, con spezzamenti di Heegaard (U1, V1) e

(U2, V2). Siano R1 ⊂ ∂−U1 e R2 ⊂ ∂−U2 due componenti connesse omeomorfe

mediante un omeomorfismo g, e poniamo R0

i = ∂−Ui\ Ri, per i = 1, 2. Allora Ui si

costruisce attaccando 1-manici a (Ri∪ R0i) × I; pertanto rimuovendo tali 1-manici

otteniamo una 3-variet`a U0

i, le cui componenti connesse sono omeomorfe ad un

prodotto F ×I, con F superficie compatta chiusa. Chiameremo hil’omeomorfismo

della componente connessa Qi di Ui0 contenente Ricon Ri× I. Sia pi : Ri× I → Ri

la proiezione sul primo fattore.

Imponiamo su M1t M2 la seguente relazione di equivalenza (i = 1, 2):

1. se xi, yi ∈ Qi e pi(hi(xi)) = pi(hi(yi)) allora xi∼ yi;

2. se x ∈ R1, y ∈ R2 e g(x) = y, allora x ∼ y.

Ovviamente possiamo far s`ı che i dischi su Qi su cui sono attaccati gli 1-manici di

Ui abbiano immagini disgiunte in Ri, cos`ı che non vengano identificati fra di loro.

Definiamo: M = M1t M2 ∼ , W1 = U1t V2 ∼ , W2= V1t U2 ∼ .

(24)

In questo modo (W1, W2) `e uno spezzamento di (M, R01∪ ∂−V2, R02∪ ∂−V1).

Infatti W₁si ottiene attaccando degli 1-manici a V₂∪Q₁, e W₂si ottiene attaccando degli 1-manici a V1∪ Q2. U1 Σ2 Σ₁ R₁ W₁ W₂ U₂ R₂ Σ Figura 2.6: Un’amalgamazione.

Definizione 2.30. Lo spezzamento di Heegaard (W1, W2) di M cos`ı ottenuto si chiama amalgamazione di (U1, V1) e (U2, V2) lungo R1 e R2.

Osservazione 2.31. Detti g_i il genere di Σ_i= U_i∩ V_i, per i = 1, 2, e g il genere di Σ = W1∩ W2, vale la seguente relazione, dove gR `e il genere di R = R1 ∼= R2:

g = g1+ g2− gR

Se Σ `e uno spezzamento di Heegaard debolmente riducibile, possiamo trovare un insieme massimale ∆ di dischi di compressione per Σ tale che ∆ ∩ Wi contenga

almeno un disco per i = 1, 2. Indicheremo con Σ∗_{la superficie ottenuta da σ(Σ; ∆)}

eliminando eventuali componenti connesse sferiche. Valgono i seguenti due lemmi.

Lemma 2.32. Sia (W1, W2) uno spezzamento di Heegaard debolmente riducibile di una 3-variet`a M con superficie di Heegaard Σ, e sia ∆ un insieme massimale di dischi di compressione per Σ tale che ∆∩Wi contenga almeno un disco per i = 1, 2.

Sia N la chiusura di una componente connessa di M \ Σ∗_{. Allora (W}

1, W2) induce uno spezzamento di Heegaard (U₁, U₂) di N tale che ∂N \ ∂M `e contenuto o in

∂−U1 o in ∂−U2.

Dimostrazione. Chiamiamo ∆i i sottoinsiemi di ∆ tali che ∆ = ∆1∪ ∆2 e ∆i `e

formato da dischi di compressione per Wi.

Senza perdita di generalità, possiamo supporre N ⊂ W1∪ η(∆2), e poniamo U1 = W1 ∩ N e U2 = N \ U1. Poiché N è ottenuto attaccando 2-manici a U1,

questo si ottiene da N rimuovendo 2-manici, e pertanto `e connesso. Quindi U1

è una componente connessa di W1 \ η(∆1) ed è un compression body. Invece U2 si ottiene attaccando 2-manici ad un collare di Σ∗. Inoltre è connesso in

(25)

quanto ∂+U1 = ∂−U2, e quindi `e un compression body. Pertanto (U1, U2) `e uno

spezzamento di Heegaard di N .

Lemma 2.33. Sia (W₁, W₂) uno spezzamento di Heegaard debolmente riducibile

di una 3-variet`a M con superficie di Heegaard Σ, e ∆ una famiglia massimale di dischi di compressione per Σ tale che ∆ ∩ Wi contenga almeno un disco per

i = 1, 2. Chiamiamo N₁, ..., N_n le chiusure delle componenti connesse di M \ Σ∗_,

e chiamiamo (U1

1, U21), ..., (U1n, U2n) gli spezzamenti di Heegaard indotti come nel Lemma 2.32. Allora (W1, W2) `e l’amalgamazione di (U11, U21), ..., (U1n, U2n) lungo

Σ#_{= (}S_∂N

i) \ ∂M .

Dimostrazione. Procediamo per induzione su n. Se le componenti connesse di M \Σ#sono due, per definizione (W1, W2) `e l’amalgamazione di (U11, U21), (U12, U22).

Altrimenti, poniamo ∆0 _{= ∆∩N}

1, e sia ∆00= ∆\∆0. Analogamente definiamo

Σ∗0_{, Σ}∗00_{, Σ}#0_{, Σ}#00_{. Allora M \ Σ}∗0 _{ha due componenti connesse, le cui chiusure}

sono N1 e N = N2∪ ... ∪ Nn. Inoltre, N2, ..., Nnsono le chiusure delle componenti

connesse di N \ Σ∗00_.

Allora lo spezzamento di Heegaard (V1, V2) indotto su M \ N1 induce

sul-le componenti N₂, ..., N_n degli spezzamenti di Heegaard equivalenti agli spezza-menti (U2

1, U22), ..., (U1n, U2n). Per ipotesi induttiva, (V12, V22) `e l’amalgamazione

di (U2

1, U22), ..., (U1n, U2n) lungo Σ#00. Come nel caso n = 2, (W1, W2) `e

l’amal-gamazione di (U1

1, U21) e (V1, V2) lungo Σ#0; poich´e Σ# = Σ#0∪ Σ#00, si ha la

tesi.

2.3 Spezzamenti di handlebody

In un handlebody H c’`e un modo semplice di costruire uno spezzamento di Heegaard: si prende come superficie Σ una superficie parallela a ∂H.

Definizione 2.34. Uno spezzamento di Heegaard Σ di un handlebody H si dice banale se Σ `e parallela a ∂H. Si dice invece standard se si ottiene mediante

stabilizzazione di uno spezzamento di Heegaard banale.

Proposizione 2.35. Ogni spezzamento di Heegaard di un handlebody H `e

stan-dard.

Dimostrazione. Sia Σ la superficie di Heegaard; essa divide H in un handlebody H₁ ed un compression body H₂. Sia n ≥ 1 il genere di H.

Se n = 0 abbiamo H = D3, e il teorema segue subito dal Teorema 2.23. Sia ∆ un sistema completo di dischi per H trasversale a Σ, e supponiamo che esista D ∈ ∆ tale che D ∩ Σ 6= ∅ (il caso Σ ⊂ H \ ∆ sar`a trattato pi`u avanti). Allora D ∩ Σ consiste di curve chiuse semplici αi per i = 1, ..., m; se qualcuna

di queste curve `e inessenziale in Σ, possiamo eliminarla con un’isotopia di Σ, in quanto H `e irriducibile. Quindi possiamo supporre che D ∩ Σ sia formato da curve tutte essenziali in Σ. Sia α¯ıuna di tali curve, e chiamiamo B¯ıil disco bordato da α¯ıin D.

(26)

Scegliamo una curva chiusa semplice σ¯ıtrasversale a ∆ e tale che valga σ¯ı∩D = σ_¯ı∩∆ = {p_¯ı} ⊂ D\S_¯ıB_¯ıe σ_¯ı∩Σ = ∅, e fissiamo un intorno tubolare η(σ_¯ı) ∼= D2×I

in modo che σ¯ıcorrisponda a {0} × I. Sia ¯η(D) ∼= D × [−1, 1] un intorno tubolare

di D tale che D corrisponda a D × {0}.

Sia Q una spina per H1; a meno di isotopia possiamo supporre Q ∩ ∂ ¯η(D) = {q+, q−}. Allora, scelti archi semplici ρ+ ⊂ D × {1} e ρ− ⊂ D × {−1} tali che

∂ρ+ = {q+} ∪ (σ ∩ (D × {1})) e ∂ρ− = {q−} ∪ (σ¯ı∩ (D × {−1})), poniamo Q0 _{= (Q \ (Q ∩ ¯}_{η(D))) ∪ ρ} +∪ ρ−∪ (σ¯ı\ (σ¯ı∩ ¯η(D))), e siano H10 = ¯η(Q0) e H \ H10, e Σ0 = H₁0 ∩ H₂0 = ∂ ¯η(Q0) (Figura 2.7). spina di H1 spina di H1´ D σ¯ı p¯ı Figura 2.7: La superficie Σ0_.

Ripetiamo ora la costruzione fatta per tutte le curve α_i ⊂ D, e per tutti i dischi D ∈ ∆ tali che D ∩ Σ 6= ∅. In questo modo otteniamo una superficie di genere g0_{, che indichiamo ancora con Σ}0_{, disgiunta da un sistema completo di dischi per}

H, e quindi contenuta in una palla P . Se g0 _{> 1, esiste una curva chiusa semplice}

τ ⊂ Σ0 _{che borda un disco δ}

1 ⊂ H1 e tale che Σ0\ τ sia sconnessa. Scegliamo un

anello A propriamente embedded in P \ Σ0 _{tale che τ ∂A τ ∪ ∂P ; possiamo}

scegliere A in modo che ∂A \ τ tagli ∂P in due dischi, uno contenente una copia

D × {1} di un disco e l’altro contenente D × {−1}. In questo modo abbiamo

costruito un disco δ = A ∪ δ1 propriamente embedded in H che interseca H1 in

un disco e H₂ in un anello.

Nel caso in cui Σ ⊂ H \ ∆, con la tecnica appena impiegata possiamo costruire un disco δ tale che δ ∩ H1 sia un disco e δ ∩ H2 sia un anello.

Se invece g0 _{= 1, sia τ un meridiano di Σ}0 _{tale che τ ⊂ H \ ¯}_η(S

¯ı,Dσ¯ı) per

tutte le curve σ utilizzate nella costruzione di Σ0; allora troviamo un anello A propriamente embedded in M \ Σ tale che τ ⊂ ∂A ⊂ τ ∪ ∂H. Anche in questo caso possiamo costruire un disco D propriamente embedded in H che interseca

H1 in un disco e H2 in un anello. Osserviamo che non pu`o essere g0 = 0 perch´e n 6= 0.

Comprimiamo H1 lungo D ∩ H1, ottenendo un handlebody H10, poi

(27)

H0

2 = H0\ H10 `e un compression body, pertanto abbiamo uno spezzamento di

Hee-gaard di H0_{. Per ipotesi induttiva, se non è banale esso è standard; se è banale, è}

banale anche quello di H, e se `e standard anche quello di H `e standard.

2.4 Spezzamenti di F × I

In tutta questa sezione F sarà una superficie orientabile, compatta e chiusa. In questa sezione vengono dati sue esempi “banali” di spezzamenti delle varietà del tipo F × I, dopodiché vengono dimostrate le Proposizioni 2.41 e 2standardsse, che caratterizzano quegli spezzamenti che si ottengono stabilizzando tali spezzamenti “banali”. Scelta una funzione di Morse h che caratterizza uno spezzamento, con un ragionamento di posizione magra viene mostrato (Lemma 2.43) che se h ha pi`u di un punto critico su un arco isotopo a {p}×I, lo spezzamento è debolmente ridu-cibile, e la Proposizione 2.46 mostra che ogni spezzamento debolmente riducibile è in effetti riducibile. Per concludere, la Proposizione 2.45 mostra che se sull’arco considerato in precedenza h ha non pi`u di un punto critico, lo spezzamento è ba-nale oppure riducibile. Mettendo insieme tali risultati, e grazie alla Proposizione 2.25 si ottiene (Teorema 2.47) che ogni spezzamento irriducibile di F × I si ottiene stabilizzando uno spezzamento “banale”.

Lemma 2.36. Ogni anello quasi verticale essenziale A ⊂ F × I `e isotopo ad un

anello verticale γ × I.

Dimostrazione. Siano γ_i ⊂ F , per i = 1, 2, curve semplici chiuse in F tali che ∂0A = A ∩ (F × {0}) = γ0× {0} e ∂1A = A ∩ (F × {1}) = γ1× {1}. In F × I le

curve γ1×{1} e γ0×{0} sono omotope, e quest’ultima curva `e omotopa a γ0×{1}.

Identificando F con F × {1}, otteniamo che γ₀ e γ₁ sono omotope in F . Poich´e esse sono curve embedded, sono isotope ([E]). Quindi a meno di isotopia possiamo supporre che γ0= γ1.

Incolliamo le basi di F × I mediante la relazione di equivalenza (p, 0) ∼ (p, 1), ottenendo F × S1_{. Sia T il toro ottenuto incollando fra loro le basi di A. Poich´e} π1(F × S1) ∼= π1(F ) × π1(S1), l’inclusione π1(T ) → π1(F × S1) `e iniettiva,

pertanto T `e incompressibile in F × S1_{. Per il Lemma 3.25, che sar`a dimostrato}

pi`u avanti in maniera indipendente, esiste un’isotopia di T che porta T ad essere un toro verticale oppure parallelo a F × {0}, e tale isotopia pu`o essere scelta in modo da fissare tutto un intorno F × [−ε, ε] di F × {0} in F × S1_{. Grazie a}

questa condizione, T non pu`o diventare parallelo a F × {0}: infatti la condizione

F × {0} ! T ∩ (F × {0}) 6= ∅ rimane vera durante tutta l’isotopia, (perch´e T `e

incompressibile, quindi T ∩ (F × {0}) è formato da curve essenziali in F × {0}) pertanto T non può diventare né la superficie orizzontale F × {0} (perché sarebbe

F × {0} = T ∩ (F × {0}), n´e una superficie orizzontale F × {t} con t 6= 0 (sarebbe T ∩ (F × {0}) = ∅).

Pertanto abbiamo trovato un’isotopia che mette T in posizione verticale. La stessa isotopia, ristretta a F × I, mette A in posizione verticale.

(28)

Definizione 2.37. Uno spezzamento di Heegaard di F × I si dice di tipo 1 se

ognuno dei compression body contiene una componente connessa di F ×∂I, mentre diremo che `e di tipo 2 se F × ∂I `e tutto contenuto in uno dei compression body.

Per convenzione, ∂₋W₂ conterr`a sempre una componente connessa di F × ∂I, mentre W1 potr`a essere un handlebody.

Descriviamo ora due spezzamenti di Heegaard di F × I.

Esempio 2.38. La superficie Σ = F × {1/2} d`a luogo ad uno spezzamento di Heegaard di tipo 1.

Esempio 2.39. Sia γ = {p} × I un arco verticale, e D ⊂ F un piccolo disco centrato in p. Sia W2 un intorno regolare di (F × ∂I) ∪ γ, e W1 = (F × I) \ W2.

Allora W2 `e chiaramente un compression body, mentre W1 `e un handlebody in

quanto `e omeomorfo a (F \ D) × I. In questo modo si ottiene uno spezzamento di Heegaard di tipo 2.

Definizione 2.40. Gli spezzamenti di Heegaard di F × I descritti negli Esempi

2.38 e 2.39 si dicono banali.

Uno spezzamento di Heegaard sar`a detto standard se si ottiene stabilizzando uno spezzamento di Heegaard banale.

Proposizione 2.41. Uno spezzamento di Heegaard di F × I `e standard se e solo

se esiste un anello quasi verticale essenziale contenente una spina di W2.

Dimostrazione. Se uno spezzamento di Heegaard di F × I `e standard, `e evidente

che possiamo costruire una spina di W2 contenuta in un anello quasi verticale

essenziale. Infatti, supponiamo innanzi tutto che tale spezzamento sia banale. Una spina per W2è data da ∅ ⊂ F × I se lo spezzamento è di tipo 1, e da {p} × I se è di

tipo 2. Allora `e chiaro che si trova un anello quasi verticale essenziale A contenente tale spina. Se invece lo spezzamento di Heegaard `e stabilizzato, possiamo scegliere come cuori degli 1-manici da attaccare a W2 delle curve contenute in A.

Dimostriamo ora il viceversa. Sia Q una spina di W2 contenuta in un anello

quasi verticale essenziale A.

Se Q = ∅, allora W2∼= F × I, e abbiamo uno spezzamento di Heegaard banale

di tipo 1.

Altrimenti, per il Lemma 2.36 possiamo supporre che A sia verticale. Sia τ un arco quasi verticale contenuto in Q; a meno di isotopia possiamo supporre che anche τ sia verticale. Se Q = τ abbiamo uno spezzamento di Heegaard banale di tipo 2.

Se invece Q 6= ∅ e Q non `e costituita da un arco quasi verticale, troviamo una disco D ⊂ A \ Q tale che σ = ∂D `e omotopicamente banale in A. Allora consi-deriamo l’1-manico di W₂ dato dall’intorno tubolare ¯η(σ) ∼= D2× [0, 1] in W₂; sia

D00 = D2×{1/2}; allora D00e D∩W1sono due dischi, il primo propriamente

(29)

Pertanto lo spezzamento di Heegaard `e stabilizzato; sia (W0

1, W20) la

destabilizza-zione di (W₁, W₂): una sua spina `e Q \ σ ⊂ A. Possiamo quindi destabilizzare (W1, W2) fino ad ottenere uno spezzamento banale di tipo 2.

Per gli spezzamenti di tipo 2 abbiamo il seguente risultato pi`u forte.

Proposizione 2.42. Uno spezzamento di Heegaard di F × I di tipo 2 `e standard

se e solo se esiste una spina di W2 contenente un arco quasi verticale contenuto in un anello quasi verticale essenziale.

Dimostrazione. Dato uno spezzamento di Heegaard standard di tipo 2, l’esistenza

di una spina con le propriet`a richieste segue subito dalla Proposizione 2.41. Sup-poniamo invece che esista una spina Q di W2 contenente un arco quasi verticale γ

contenuto in un anello quasi verticale A. Allora per il Lemma 2.36 con un’isotopia possiamo rendere A verticale, e possiamo anche far s`ı che γ sia trasformato in un arco verticale.

Sia η(γ) un intorno tubolare di γ in W2. Allora H = (F × I) \ η(γ) `e un

handlebody. La rimozione di η(γ) da W₂ equivale alla rimozione di un 2-manico, pertanto W2\ η(γ) `e ancora un compression body. Quindi ∂+W2 definisce uno

spezzamento di Heegaard per H.

Per la Proposizione 2.35 tale spezzamento si ottiene stabilizzando lo spezza-mento banale, che corrisponde allo spezzaspezza-mento banale di tipo 2 su F ×I, pertanto abbiamo la tesi.

Adesso abbiamo gli strumenti per studiare gli spezzamenti di Heegaard delle variet`a F × I.

Sia Σ, di genere g > 1, la superficie che determina uno spezzamento di Hee-gaard di F × I, e siano W1 e W2 i compression body risultanti. Scegliamo un

sistema completo minimale di dischi per W1 ed uno per W2; in questo modo

possiamo costruire tali compression body senza utilizzare alcun 3-manico per W₂ (ricordiamo che per convenzione W2 non `e un handlebody), ed utilizzandone al

pi`u uno per W1.

Sia h una funzione di Morse rispetto a F × ∂I che definisce tale spezzamento di Heegaard. Inoltre, scegliamo un arco γ = {p} × I; possiamo fare in modo che

h|γ sia in posizione generica ed in posizione magra rispetto ad h.

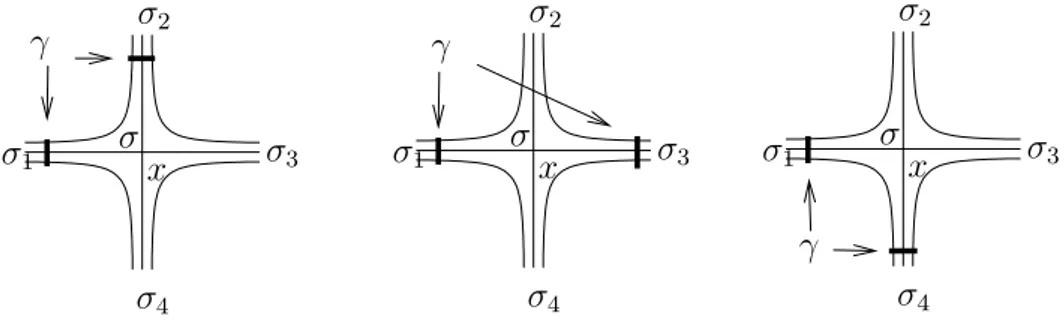
Lemma 2.43. Se h|_γ ha pi`u di un punto critico, Σ `e debolmente riducibile. Dimostrazione. Sia σ1, ..., σ2g una famiglia di curve in F tali che σj∩ σk= {p} se

j 6= k e che F \S2g_i=1αi sia un disco. Sia Pi = σi× I; se tagliamo F × I lungo tali

anelli otteniamo un prisma G con facce laterali A_l, per l = 1, ..., 4g; indichiamo con A la superficie laterale di G. Possiamo scegliere le curve σi in modo che h|∪Pi

sia di Morse e i suoi valori critici siano distinti dai valori critici di h e di h|γ.

Diremo che un arco τ propriamente embedded in A_l`e inessenziale se esiste un arco τ0 ⊂ γ tale che τ ∪ τ0 borda un disco in Al. Invece diremo che τ `e essenziale

(30)

sar`a detta strettamente essenziale se interseca ogni faccia di G soltanto in archi essenziali. Gli archi aventi un estremo su γ ed uno su una base di G non verranno utilizzati nell’argomento che segue.

Se h|γ ha pi`u di un punto critico, siano m il pi`u grande valore di minimo e M

il pi`u piccolo valore di massimo tale che M > m.

Scegliamo r ∈ (m, M ) in modo che h−1(r) sia trasversale a tutte le facce di

G, e supponiamo che h−1_{(r) intersechi una delle facce A}

l in un arco inessenziale.

Sia λ uno di tali archi, scelto in modo che il disco D ⊂ A_l tale che ∂D ⊂ λ ∪ γ non contenga altri archi inessenziali, e sia λ0 tale che ∂D = λ ∪ λ0. Poiché k è in posizione magra, grazie al Lemma 1.25 nessun livello è contemporaneamente alto e basso.

Poniamo

B = {α ∈ (m, M ) tali che α `e un livello alto}

e

S = {α ∈ (m, M ) tali che α `e un livello basso}.

Vogliamo dimostrare che B ∪ S 6= [m, M ].

Se U `e un intervallo aperto contenuto in (m, M ), vale U ⊂ B oppure U ∩B = ∅, e la stessa cosa vale per S. Inoltre, m ∈ B e M ∈ S. Pertanto, se per assurdo fosse B ∪ S = [m, M ], troveremmo r per il quale h−1_{(r) e A}

l sarebbero tangenti, con (r − ε, r) ⊂ B e (r, r + ε) ⊂ S. σ2 σ4 σ3 σ1 σ _x 1_γ− ε 1γε+ 2_γ+ ε 2γε− Figura 2.8: Le foglie di h|_∂G.

Osserviamo che il punto di tangenza x fra h−1_{(r) e A}

lnon pu`o essere un centro:

in un intorno V di un centro, infatti, le curve di livello di h|_∂G sono curve chiuse; quindi il disco alto D_ε+0 relativo al livello r − ε0 ed il disco basso D_ε−0 relativo al