Capitolo 4 I sistemi di riferimento e le matrici di rotazione

Capitolo 4

I sistemi di riferimento e le matrici di rotazione

Al fine di rendere la definizione delle grandezze più semplice, viene utilizzato il sistema di riferimento globale del velivolo e anche dei sistemi di riferimento locali per l'ala anteriore, posteriore e per la paratia.

Per passare da un riferimento ad un altro è necessario costruire le matrici di rotazione, dell'ala anteriore, posteriore e della paratia. Tali matrici sono realizzate portando il sistema globale a coincidere con quello locale, attraverso una serie di rotazioni elementari. Per descrivere correttamente tali rotazioni occorre conoscere gli angoli formati dalla proiezione dell'ala sui piani del sistema di riferimento globale.

La nomenclatura utilizzata per i due sistemi di riferimento è la seguente:

• sistema di riferimento globale del velivolo (O, X, Y, Z)

• sistema di riferimento locale delle ali (o, x, y, z)

4.2 Il sistema di riferimento globale del velivolo

Per sistema di riferimento globale si definisce il sistema di figura 4.1 con:

• l'origine O in corrispondenza del muso del velivolo;

• l'asse X orizzontale diretto lungo l'asse longitudinale del velivolo e avente la direzione del

flusso asintotico;

• l'asse Z verticale diretto come il filo di piombo con verso positivo verso l'alto;

4.3 Il sistema di riferimento locale dell'ala

Il sistema di riferimento locale dell'ala è stato scelto in modo che gli assi abbiano questa orientazione:

• asse x è il luogo dei centri di taglio delle sezioni alari lungo l'apertura;

• asse y diretto lungo la corda media aerodinamica (dal bordo di attacco al bordo di uscita);

• asse z diretto in modo da rendere la terna levogira.

L'origine e l'orientazione dell'asse x sono diversi in base all'ala considerata: la scelta è stata quella di considerare l'ascissa x delle ali come se venissero percorse in modo continuo dalla radice dell'ala posteriore alla radice dell'ala anteriore; così facendo il calcolo delle cds sarà più immediato. Tutto questo verrà approfondito nel capitolo relativo al calcolo delle cds.

Si ha quindi che:

• per l'ala posteriore l'origine è alla radice dell'ala e l'asse x va dal root al tip; Fig.4.1

• per il bulk l'origine è all'incastro tra l'ala posteriore e il bulk e l'asse x va dall'incastro con l'ala posteriore a quello con l'ala anteriore;

• per l'ala anteriore l'origine è al tip dell'ala e l'asse x va dal tip al root.

La figura 4.2 illustra origine e orientazione dei sistemi di riferimento locali.

4.4 Proiezione dell'ala sui piani definiti dal sistema di riferimento principale

Per definire correttamente la matrice di rotazione elementare si introducono gli angoli formati dalla proiezione dell'ala sui piani formati dal sistema di riferimento globale del velivolo. Tali angoli sono dunque l'angolo di freccia Λ sul piano X-Y, l'angolo diedro sul piano Y-Z, l'angolo sul piano X-Z dell'ala. Gli angoli di freccia e di diedro sono riferiti all'asse al 25% della corda media aerodinamica, tuttavia tale asse si suppone coincidente con l'asse elastico dell'ala, e quindi con l'asse x locale. I segni degli angoli differiscono da quelli in uscita da ASD e da quelli utilizzati convenzionalmente.

Fig 4.2 Ala posteriore

Bulk

4.4.1 Angolo di freccia Λ nel piano X-Y

Piano X-Y globale → angolo di freccia Λ al 25% della corda media aerodinamica:

• per l'ala anteriore è l'angolo formato tra l'asse x locale e l'asse Y globale: il senso positivo di

rotazione è antiorario;

• per l'ala posteriore è l'angolo formato tra l'asse x locale e l'asse Y globale: il senso positivo

di rotazione è orario;

• per la paratia è l'angolo tra l'asse x locale e l'asse X globale: il senso positivo di rotazione è

antiorario. Λ_{ALA POSTERIORE} x loc AP Λ_{ALA ANTERIORE} x loc AA x lo c B U L K Λ _BULK Fig. 4.3 Y_GLOBALE X G L O B A L E O

L'angolo di “freccia” della paratia è dato dalla seguente relazione:

Λbulk=arctg (

Y.tip.ap−Y.tip.aa

X.bulk )

Per esempio in figura 4.3 gli angoli di freccia dell'ala anteriore e posteriore sono negativi mentre quello della paratia è positivo.

4.4.2 Angolo diedro Γ nel piano Y-Z

Piano Y-Z globale → angolo di diedro Γ:

• per l'ala anteriore è l'angolo formato tra l'asse x locale e l'asse Y globale: il senso positivo di

rotazione è antiorario;

• per l'ala posteriore è l'angolo formato tra l'asse x locale e l'asse Y globale: il senso positivo

di rotazione è antiorario;

• per la paratia è l'angolo tra l'asse x locale e l'asse X globale: il senso positivo di rotazione è

antiorario.

- Y.tip.ap è la coord. del tip dell'ala post. lungo Y del sist. globale;

- Y.tip.aa è la coord. del tip dell'ala ant. lungo Y del sist. globale;

- X.bulk è la lunghezza del bulk lungo X del sist. globale

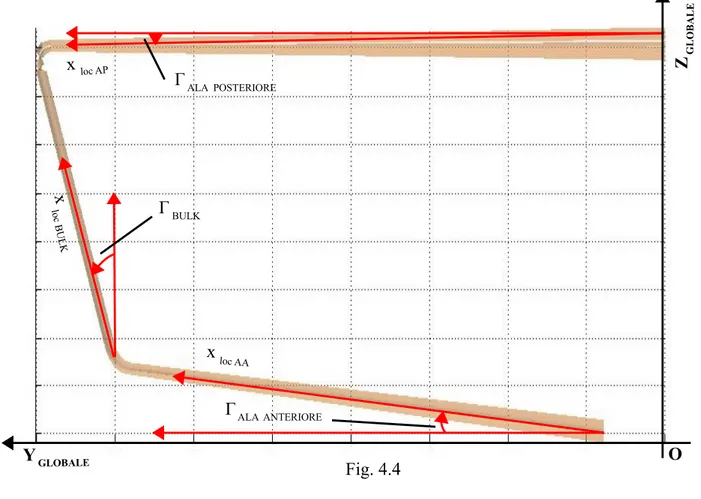
Fig. 4.4 dove: Γ _{ALA ANTERIORE} Γ _BULK Γ _{ALA POSTERIORE} O Z G L O B A L E Y _GLOBALE x _{loc AP} x _{loc AA} x lo c B U L_K

L'angolo di diedro del bulk è ottenuto tramite la seguente relazione:

Γ_bulk=arctg (Y.tip.ap−Y.tip.aa

Z.bulk )

Per esempio in figura 4.4 l'angolo Γ dell'ala posteriore e del bulk sono positivi mentre l'angolo Γ dell'ala anteriore è negativo.

4.4.3 Angolo φ nel piano X-Z

Piano X-Z globale → angolo φ:

• per l'ala anteriore è l'angolo formato tra l'asse x locale dell'ala anteriore e l'asse X globale: il verso positivo è antiorario. Si ottiene per mezzo della relazione:

ψ_{ala.anteriore}=arctg (Z.aa

X.aa) Z.aa=(b.aa−Y.aa.root )∗tg Γaa

X.aa=(b.aa−Y.aa.root )∗tg Λ_aa

• per l'ala posteriore è l'angolo formato tra l'asse x locale dell'ala posteriore e l'asse X globale:

il verso positivo è orario. Con significato dei simboli identico all'ala anteriore si ottiene:

ψ_{ala.posteriore}=arctg (Z.ap

X.ap) Z.ap=(b.ap−Y.ap.root)∗tg Γap

X.ap=(b.ap−Y.ap.root)∗tg Λap

- Z.aa è la lunghezza dell'ala ant. lungo Z globale - X.aa è la lunghezza dell'ala ant. lungo X globale - b.aa è la coord. al tip dell'ala ant. lungo Y globale - Y.aa.root è la coord. al root dell'ala ant lungo Y globale - Γaa è l'angolo di diedro dell'ala ant

- Λaa è l'angolo di freccia dell'ala ant

con con

- Y.tip.ap è la coord. del tip dell'ala post. lungo Y del sist. globale;

- Y.tip.aa è la coord. del tip dell'ala ant. lungo Y del sist. globale;

- Z.bulk è la lunghezza del bulk lungo Z del sist. globale dove:

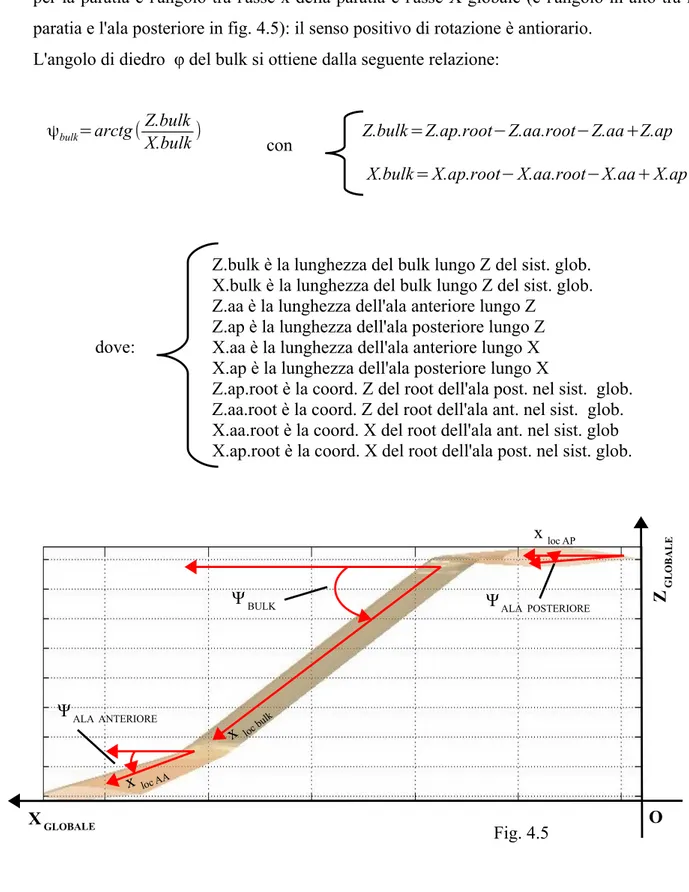
• per la paratia è l'angolo tra l'asse x della paratia e l'asse X globale (è l'angolo in alto tra la paratia e l'ala posteriore in fig. 4.5): il senso positivo di rotazione è antiorario.

L'angolo di diedro φ del bulk si ottiene dalla seguente relazione:

ψ_bulk=arctg (Z.bulk

X.bulk) Z.bulk=Z.ap.root−Z.aa.root−Z.aa+Z.ap

X.bulk= X.ap.root− X.aa.root−X.aa+ X.ap

Per esempio in figura 4.5 l'angolo φ dell'ala posteriore è negativo, l'angolo φ dell'ala anteriore e del bulk sono positivi.

Fig. 4.5 Z.bulk è la lunghezza del bulk lungo Z del sist. glob. X.bulk è la lunghezza del bulk lungo Z del sist. glob. Z.aa è la lunghezza dell'ala anteriore lungo Z

Z.ap è la lunghezza dell'ala posteriore lungo Z X.aa è la lunghezza dell'ala anteriore lungo X X.ap è la lunghezza dell'ala posteriore lungo X

Z.ap.root è la coord. Z del root dell'ala post. nel sist. glob. Z.aa.root è la coord. Z del root dell'ala ant. nel sist. glob. X.aa.root è la coord. X del root dell'ala ant. nel sist. glob X.ap.root è la coord. X del root dell'ala post. nel sist. glob. dove: con Z G L O BA L E X _GLOBALE O Ψ _{ALA POSTERIORE} Ψ _BULK Ψ _{ALA ANTERIORE} x _{loc AP} x loc bu lk x loc AA

4.5 Le matrici di rotazione

Le matrici di rotazione consentono di esprimere i parametri nei due sistemi di riferimento passando agevolmente da un sistema all'altro.

Poiché si effettuano le rotazioni rispetto al sistema mobile è necessario applicare la regola del post-moltiplicare.

Il sistema globale viene quindi ruotato con rotazioni elementari in modo da farlo coincidere con quello locale; in questo modo si ottiene la matrice di rotazione che consente di trasformare il vettore dal sistema locale a quello globale:

Xg R11 R12 R13 x

Yg = R21 R22 R23 ● y

Zg R31 R32 R33 z

Per effettuare l'operazione inversa, cioè per calcolare il vettore nel sistema locale noto quello nel sistema globale è necessario calcolare l'inversa della matrice di rotazione precedentemente calcolata:

x R11 R12 R13 Xg

y = R21 R22 R23 ● Yg

z R31 R32 R33 Zg

Nei paragrafi seguenti si riporta nel dettagliato la costruzione delle matrici di rotazione dal sistema locale a quello globale per l'ala anteriore, posteriore e per il bulk.

Coordinate nel sist. locale Vettore nel

sist. globale

Matrice di rotazione

sistema locale → sistema globale

Coordinate del vettore nel sist. globale

Coordinate del vettore

nel sist. locale Matrice di rotazione _{sistema globale → sistema locale}

4.5.1 La matrice di rotazione dell'ala anteriore

Oltre agli angoli di freccia e di diedro dell'ala anteriore definiti nel paragrafo 4.4, occorre introdurre un ulteriore angolo che caratterizza la matrice di rotazione dell'ala anteriore: l'angolo diedro effettivo Γ'. Quest'angolo è compreso tra la proiezione di x locale dell'ala anteriore con il piano X-Y globale e l'asse x locale stesso, così come schematizzato in figura 4.6.

L'angolo diedro effettivo dell'ala anteriore si ottiene attraverso la seguente relazione: tang( Γ' ) = tang( Γ ) · cos( Λ )

Per allineare i due sistemi occorre eseguire le seguenti rotazioni: 1) Rotazione di π/2 + Λ attorno all'asse Z globale:

X

Y

Z

in blu: riferimento mobile in rosso: riferimento fisso

X

Y

Z

Proiezione asse x locale sul piano X-Y Proiezione asse x locale sul piano Y-Z

Γ

Γ'

Fig 4.6

Con la rotazione R1 l'asse X globale coincide con la proiezione dell'asse x locale sul piano X-Y del sistema globale. Il sistema di riferimento ottenuto dopo la prima rotazione verrà chiamato (O,X',Y',Z').

La corrispondente matrice di rotazione associata alla rotazione elementare è:

cos(π/2+Λ) -sen(π/2+Λ) 0 -sen(Λ) -cos(Λ) 0

[R1] = sen(π/2+Λ) cos(π/2+Λ) 0 = cos(Λ) -sen(Λ) 0

0 0 1 0 0 1

2) Rotazione di Γ' (angolo di diedro effettivo) attorno all'asse Y':

Con la rotazione R2 l'asse X' coincide con l'asse x locale e le due terne combaciano. La corrispondente matrice di rotazione associata alla rotazione elementare è:

cos(Γ') 0 -sen(Γ')

[R2] = 0 1 0 sen(Γ') 0 cos(Γ')

La matrice di rotazione dell'ala anteriore ottenuta per composizione delle due rotazioni elementari è:

sen(Λ)·cos(Γ') cos(Λ) -sen(Λ)·sen(Γ')

[Ra]= [R1]·[R2]= -cos(Λ)·cos(Γ') sen(Λ) cos(Λ)·sen(Γ')

sen(Γ') 0 cos(Γ')

X'

Y'

Z'

in blu: riferimento mobile in rosso: riferimento fisso

4.5.2 La matrice di rotazione dell'ala posteriore

La procedura utilizzata per determinare la matrice di rotazione dell'ala posteriore segue la stessa procedura dell'ala anteriore, con l'aggiunta di un ulteriore rotazione di 180° attorno all'asse x ottenuto dopo la seconda rotazione per allineare le due terne.

4.5.3 La matrice di rotazione del bulk

Anche per il bulk si fa riferimento all'angolo di diedro effettivo, che in questo caso rappresenta l'angolo tra l'asse x locale e la proiezione di questo sul piano X-Z globale, così come in figura 4.9:

Dalla figura si intuisce che l'angolo di diedro effettivo è dato dalla seguente rotazione: tang( Γ' ) = tang( Γ ) · cos( θ )

Per comodità nelle matrici di rotazione si utilizza l'angolo θ che come evidenziato in figura è uguale a: θ = π/2 – φ.

Per allineare le due terne occorre effettuare le seguenti rotazioni:

X

Y

Z

φ

Proiezione asse x locale sul piano X-Z Proiezione asse x locale sul piano Y-Z

Γ

Γ'

θ

1) Rotazione di π + φ attorno all'asse Y del sistema globale:

Con la rotazione R1 l'asse X globale coincide con la proiezione dell'asse x locale sul piano X-Y globale, e l'asse Z' coincide con l'asse y locale, ottenendo la nuova terna (O,X',Y',Z'). La corrispondente matrice di rotazione associata alla rotazione elementare è:

cos(π+φ) 0 sin(π+φ) -cos(φ) 0 -sin(φ)

[R1] = 0 1 0 = 0 1 0

-sin(π+φ) 0 cos(π+φ) sin(φ) 0 -cos(φ)

poiché φ = π/2 - θ sostituendo si ha:

-cos(π/2-θ) 0 -sin(π/2-θ) -sen(θ) 0 -cos(θ)

[R1] = 0 1 0 = 0 1 0

sin(π/2-θ) 0 -cos(π/2-θ) cos(θ) 0 -cos(θ)

X

Y

Z

in blu: riferimento mobile in rosso: riferimento fisso

Fig 4.10

2) Rotazione di Γ' (angolo di diedro effettivo) attorno all'asse Z':

Dopo questa rotazione R2 l'asse X' coincide con l'asse x locale, il sistema ottenuto è denominato (O,X'',Y'',Z''). La matrice di rotazione associata a questa rotazione è:

cos(Γ') -sen(Γ') 0

[R2] = sen(Γ') cos(Γ') 0 0 0 1

3) Rotazione attorno all'asse X'' di π/2:

Dopo questa terza rotazione le due terne coincidono. La matrice associata alla rotazione elementare è la seguente:

X'

Y'

Z'

in blu: riferimento mobile in rosso: riferimento fisso

Fig 4.11

X''

Y''

Z''

in blu: riferimento mobile in rosso: riferimento fisso

1 0 0

[R3] = 0 0 -1 0 1 0

La matrice di rotazione del bulk è dunque uguale ottenuta moltiplicando le precedenti matrici di rotazione elementare è:

sen(θ)·cos(Γ') cos(θ) -sen(θ)·sen(Γ')

[Rbulk] = [R1] · [R2] · [R3] = -sen(Γ') 0 -cos(Γ')

-cos(θ)·cos(Γ') sin(θ) sen(Γ')·cos(θ)

4.6 Nomenclatura utilizzata nel programma

All'interno del programma le matrici di rotazione dell'ala anteriore, bulk e ala posteriore sono definite nel file “mattrasf”; esse verranno richiamate digitando Trasf seguito da un numero indicante l'ala considerata: Trasf1 per l'ala anteriore,Trasf2 per il bulk, Trasf3 per l'ala posteriore. Ad esempio per passare da un generico vettore nel sistema locale al corrispettivo nel sistema globale dell'ala anteriore si deve digitare:

[X;Y;Z] = Trasf1 · [x;y;z]

4.7 La lunghezza effettiva dell'ala

I carichi e le cds vengono definiti nelle sezioni in cui è stata discretizzata l'ala; per questo motivo, è necessario valutare la lunghezza effettiva dell'ala.

Il calcolo della lunghezza effettiva dell'ala, che avviene per mezzo di parametri geometrici quali la lunghezza lungo gli assi globali della proiezione delle ali e gli angoli definiti nel paragrafo 4.4 Si può utilizzare una tra le due seguenti formule:

• L_eff=

√

• L_eff= d

cos(Γ ')cos(Λ) con:

b è la lunghezza dell'ala lungo X nel sistema di rif. glob. c è la lunghezza dell'ala lungo Z nel sistema di rif. glob. d è la lunghezza dell'ala lungo Y nel sistema di rif. glob.

d è la lunghezza dell'ala lungo Y nel sistema di rif. glob. Γ' è l'angolo di diedro effettivo