Capitolo 5

(1)

Capitolo 5

Procedura sperimentale e risultati

5.1 Bitume testato

La caratterizzazione reologica è stata effettuata sul bitume RVC base e su tre miscele bitume–LLDPE mostrate nel capitolo 4 rispettivamente con percentuale di polimero del 2%, 4% e 6%.

Ricordiamo che le tre miscele si erano mostrate incompatibili, instabili allo stoccaggio e avevano dato una TP&A (temperatura di rammollimento determinata con il metodo palla e anello) come da tabella.

Tabella 5-1: temperatura di rammollimento delle 3 miscele

% polimero T di rammollimento 2 61.2 4 75.6 6 120.5

5.2 Reometro

L’analisi dinamica e le prove di viscometria sono state effettuate con un reometro rotazionale “Stresstech®” Rheologica Instruments.

Sul reometro possono essere applicati, con i pertinenti adattatori, equipaggi con geometrie diverse. Per le prove dinamiche sono state utilizzate la geometria piatto-piatto e la barra di torsione; nelle prove di viscometria è stata utilizzata soltanto la geometria piatto-piatto.

Le prove sono state effettuate in condizioni isoterme in camera termostatata; la misurazione della temperatura avviene tramite una termocoppia a contatto con il supporto inferiore del provino. Il riscaldamento della camera è effettuato per mezzo di resistenze poste sulle pareti, mentre il raffreddamento è attuato con aria

(2)

compressa per temperature medio alte o con una miscela aria/azoto per temperature inferiori ai 40°C. In questo secondo caso è immessa aria compressa (ad una pressione di poco superiore a quella atmosferica) in un serbatoio contenente azoto liquido: l’aria trascina i vapori del refrigerante e la miscela gassosa è poi introdotta nella camera attraverso appositi fori posti intorno al supporto inferiore. Il controllo delle condizioni isoterme è effettuato da un regolatore di tipo PID.

Figura 5-1: postazione di lavoro Figura 5-2: termocoppia

5.3 Analisi

dinamica

5.3.1 Modalità delle prove

Lo strumento può essere utilizzato sia in modalità “stress control” che in modalità “strain control”: nel primo caso è impostato il valore dello shear stress ed un apposito sensore misura e registra lo spostamento angolare del piatto, al quale corrisponde un certo valore della deformazione; nel secondo caso è imposta la deformazione e lo strumento registra lo stress applicato per ottenerla.

Lo strumento in realtà applica al rotore una coppia (torque) e lo stress risultante è funzione del tipo di geometria installata. Il reometro è pertanto stress control e la modalità strain control è solo “simulata” nel senso che lo strumento “cerca” il momento torcente che comporta la deformazione richiesta.

Le prove sono state condotte in strain control, applicando deformazioni di piccola entità (variabili fra 0.01% e 2% a seconda della temperatura) che permettono di

(3)

rimanere nella regione di viscoelasticità lineare del materiale. Le prove sono ugualmente valide anche se condotte in stress control, ma in questo caso è più difficile trovare i valori necessari a rimanere nella zona di comportamento lineare. Lo strumento può effettuare anche prove di creep, dove la modalità in stress

control è invece strettamente necessaria.

All’avvio del test lo strumento registra la posizione zero del piatto o del supporto superiore della barra (posizione A, Figura 5-3); una volta iniziata la prova il rotore inizia ad oscillare da B a C, passando sempre per lo zero; l’entità dell’oscillazione dipende naturalmente dalla deformazione imposta.

Le prove sono state condotte in condizioni isoterme fra -20°C e 100°C, ad intervalli di temperatura di 10°C sia con i piatti paralleli che con la barra di torsione. In ogni prova è stato investigato un intervallo di frequenze compreso fra 0.05 e 5 Hz, effettuando dieci misurazioni per ogni decade.

Figura 5-3: andamento delle oscillazioni

Prima di introdurre il campione per la prova, è necessaria una procedura di “zerogap”, effettuata in automatico dal software, per calibrare lo strumento:

• La camera viene chiusa ed è impostato il valore di temperatura alla quale effettuare il test.

• Nel caso della geometria piatto-piatto, una volta raggiunta la temperatura, il piatto superiore si abbassa fino a portarsi in contatto con quello inferiore in modo che lo strumento possa registrare l’effettiva distanza fra i piatti dopo aver introdotto il campione di bitume.

(4)

• Per la barra di torsione la procedura è analoga: fra i supporti è appoggiato un cilindretto in acciaio della stessa lunghezza della barra, ed in questo caso la testa superiore si abbassa sino a toccare il cilindro, registrando l’altezza.

5.3.2 Preparazione dei campioni

Barra di torsione

L’utilizzo della barra di torsione per la verifica delle proprietà dinamiche nei bitumi è un metodo messo a punto e testato con successo dai ricercatori dell’Università di Calgary (Canada).

Per poter effettuare le prove è stato necessario progettare uno stampo in ottone adeguato allo scopo, dove poter colare il bitume caldo già all’interno dei supporti (holder) di alluminio. Lo stampo utilizzato permette di preparare barre di queste dimensioni:

3 10

40× × mm

In realtà la lunghezza della barra sottoposta alla prova è 24 mm, in quanto le parti terminali sono inserite nel supporto.

Figura 5-4: sezione della barra

Lo stampo deve essere preliminarmente spennellato con una miscela costituita da talco e glicerina in modo che, una volta colato il bitume, i campioni raffreddati possano essere staccati facilmente dalle guide. I supporti in alluminio (tre coppie per ogni spessore) sono inseriti nelle guide e separati da un distanziale.

Lo stampo così preparato è posto in stufa a 200°C per circa 15 minuti. Questo passaggio è fondamentale perché il bitume (anch’esso riscaldato in apposito contenitore per circa mezz’ora) possa colare bene all’interno dei supporti (Figura 5-5/A); il contatto con una superficie fredda lo raffredderebbe immediatamente causando una cattiva distribuzione (Figura 5-5/B).

(5)

Figura 5-5: forma del campione

Lo stampo è lasciato raffreddare all’aria per circa 40 minuti, quindi il bitume in eccesso viene rimosso con una spatola calda e lo stampo posto in un congelatore. Le barre sono fatte scorrere fuori dalle guide (Figura 5-6) solo al momento dell’utilizzo.

Figura 5-6: estrazione dei campioni Figura 5-7: barra, distanziale e stampo

Piatto-piatto

In questo caso la preparazione dei provini consiste solamente nel colare il bitume su fogli in gomma (Figura 5-8) cercando di ottenere campioni di forma circolare con dimensioni leggermente superiori a quelle dei piatti (20 mm). Dopo raffreddamento a temperatura ambiente, i campioni sono posti in congelatore per un tempo minimo di un’ora. Tali campioni sono utilizzati anche nelle prove di viscometria con la geometria piatto-cono. Una volta posti sui piatti, l’eccesso di bitume deve essere rimosso dal bordo con l’utilizzo di una piccola spatola.

(6)

Visti i risultati ottenuti nei precedenti lavori di tesi [22], si è pensato di utilizzare anche dei piatti da 8 mm.

5.4 Master

curves

Ottenuto un numero adeguato di risultati da allineare utilizzando il principio di sovrapposizione tempo-temperatura è stata costruita la master curve secondo i passi seguenti:

• Sono stati riportati sullo stesso grafico i dati di G’, G’’ e tanδ ottenuti alle diverse temperature.

• Scelta la temperatura di riferimento (Tr = 0°C) i dati ottenuti a T≠Tr sono stati traslati ottenendo un’unica curva per ognuna delle funzioni riportate sopra.

• Gli outlier (dati fuori linea) sono stati cancellati per ottenere l’andamento effettivo.

• Contemporaneamente sono stati riportati su un altro grafico i fattori di shift in funzione della temperatura.

Come già accennato, sono utilizzate geometrie differenti a seconda della temperatura di prova. Alle basse temperature, in prossimità della transizione vetrosa, sono utilizzate sia la barra di torsione che i piatti piani da 8 mm, per le temperature superiori a 0°C invece si è optato solo per piatti piani (Tabella 5-2).

Tabella 5-2: geometrie utilizzate

Temperature di prova[°C] Geometria utilizzata -20 / -10 / 0 BT/PP8 10 / 20 PP8/PP20 Da 30 fino a 100 PP20 BT = barra di torsione

PP8 = piatto piano con diametro 8mm PP20 = piatto piano con diametro 20mm

(7)

La barra di torsione presenta risultati validi sino ad una temperatura di circa 0°C; sopra questo valore il materiale è troppo morbido e tende a flettersi durante la prova. Alle alte temperature il buono stato del materiale si può intuire dai reogrammi; più prove sullo stesso campione sono state effettuate aspettando un tempo ragionevolmente lungo fra l’una e l’altra (10-20 minuti, a seconda della temperatura) per dare la possibilità al campione di “rilassarsi”. In ogni caso non è stato possibile ottenere valori soddisfacenti oltre la terza prova (Figura 5-9 e Figura 5-10).

Figura 5-9: 1°prova Figura 5-10: 3° prova sullo stesso campione

Il confronto delle master curve ottenute dalle diverse geometrie ha comunque portato ad escludere i valori ottenuti con i piatti piani da 20 mm a temperature inferiori a 30°C. Tale conclusione è stata possibile osservando in particolare l’andamento di G’’(ω). Alla temperatura di -20°C la curva ottenuta con la barra di torsione presenta un massimo. Questo risultato corrisponde alle aspettative, in quanto il massimo di G’’(ω) individua la temperatura di transizione vetrosa, che per i bitumi è situata sempre in prossimità di questo valore. Nelle curve ottenute dalla geometria piatto-piatto G’’(ω) presenta un massimo ad una frequenza piuttosto bassa, che in questo caso corrisponde alla temperatura di 0°C.

(8)

Figura 5-11: confronto fra le geometrie

L’errata misurazione dei dati sembra essere dovuta ad un limite strumentale legato al tipo di geometria, in particolare alla dimensione del piatto.

Il torque applicato dallo strumento per ottenere una certa deformazione dà origine infatti ad uno sforzo di taglio tanto maggiore quanto minore è la superficie del piatto (si ricorda che lo sforzo di taglio ha l’unità di misura di una pressione, cioè il Pascal (Newton/m2)). Per i piatti utilizzati il massimo stress applicabile dall’apparecchiatura è 48000 Pa, che corrisponde ad un torque di 0.15 N·m. Questo valore permette di ottenere sul bitume testato una deformazione massima dello 0.5% che probabilmente con questo tipo di geometria non è alla portata della sensibilità dello strumento. Una verifica di questa teoria è stata effettuata con piatti di dimensioni minori, e la scelta è ricaduta su quelli da 8 mm che abbiamo ottenuto riducendo di diametro alcuni di quelli da 20 mm in nostro possesso. In questo caso stress più elevati hanno portato a deformazioni apprezzabili. Utilizzando i piatti da 8 mm ci siamo resi conto che con questi si potevano fare anche le prove a bassa temperatura in sostituzione della barra di torsione, stando attenti a schiacciare abbastanza il materiale (diminuendo il gap tra i due piatti) per evitare il fenomeno dello “slipping” ossia lo scorrimento del bitume a contatto con la superficie del piatto. Con il bitume base RVC non è stato possibile evitare lo slipping e quindi si è ricorsi alla barra di torsione, coi 3 bitumi modificati invece si è potuto effettuare le prove con i piatti da 8 mm con risultati soddisfacenti.

(9)

5.4.1 Master curve RVC

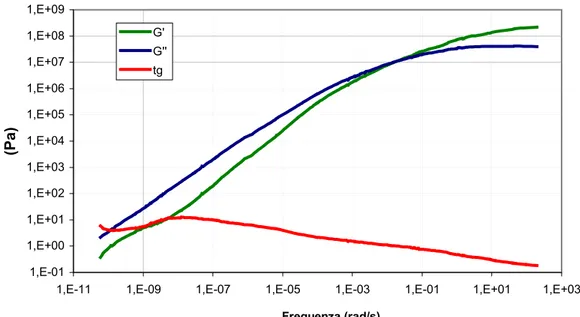
La master curve del bitume base RVC è stata ottenuta utilizzando la barra di torsione da –20°C fino a 0°C, i piatti da 8 mm da 10°C a 20°C e quelli da 20 mm per le temperature da 30°C a 60°C: oltre non si è potuti andare a causa della scarsa consistenza del bitume alle alte temperature. Come preventivato, alle basse temperature (alte frequenze) prevale G’(ω) ovvero la capacità del campione di immagazzinare energia elastica mentre dopo i 5°C prevale G’’(ω) che è connesso alla capacità di dissiparla.

Figura 5-12 Master curve RVC

1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09

1,E-08 1,E-06 1,E-04 1,E-02 1,E+00 1,E+02 1,E+04

(Pa) G' G'' tg Frequenza (rad/s)

5.4.2 Master curve miscela bitume - 2% LLDPE

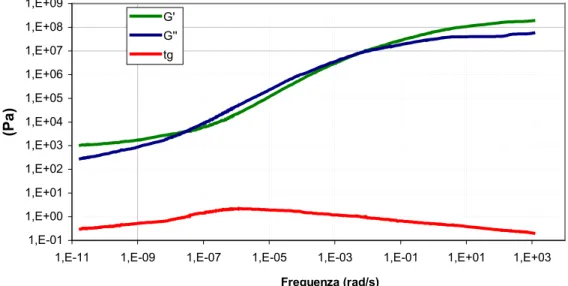
La master curve della miscela bitume-2% LLDPE è stata ottenuta utilizzando i piatti da 8 mm da –20°C fino a 20°C, e quelli da 20 mm per le temperature da 30°C a 100°C: data la maggior consistenza della miscela rispetto al bitume tal quale ci siamo potuti spingere fino a 100°C ottenendo la master curve in un range di temperatura più ampio e interessante. Anche in questo caso, alle basse temperature (alte frequenze) prevale G’(ω) mentre dopo i 5°C prevale G’’(ω)

(10)

Figura 5-13 Master curve miscela al 2% 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09

1,E-11 1,E-09 1,E-07 1,E-05 1,E-03 1,E-01 1,E+01 1,E+03

(Pa)

G' G'' tg

Frequenza (rad/s)

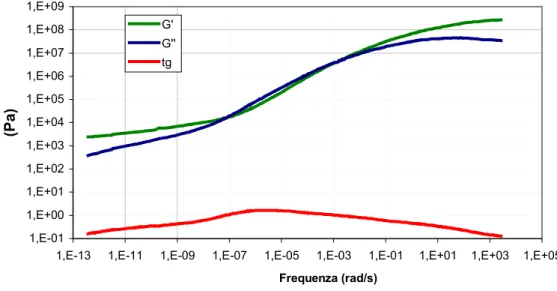
La master curve della miscela bitume-4% LLDPE è stata anch’essa ottenuta utilizzando i piatti da 8 mm da –20°C fino a 20°C, e quelli da 20 mm per le temperature da 30°C a 100°C. Anche in questo caso se era lecito attendersi la prevalenza di G’(ω) alle basse temperature e quella di G’’(ω) dopo i 15°C, sembrerebbe assurda la presenza di un secondo crossover: questo comportamento non ha significato fisico in quanto non sembra plausibile che torni a prevalere una risposta elastica del materiale. In precedenti lavori di tesi [22] si era ipotizzato che l’andamento ottenuto fosse dovuto all’inadeguatezza della geometria piatto-piatto alle alte temperature. La scarsa consistenza sarebbe stata infatti causa di errori di misurazione dovuti principalmente alla fuoriuscita del materiale dal piatto.

Abbiamo cercato in letteratura se questo fenomeno fosse stato riscontrato anche in precedenti lavori. Innanzitutto non c’è un grande numero di lavori di caratterizzazione reologica di bitumi modificati con LLDPE, mentre sono frequenti quelli con LDPE e HDPE. Però abbiamo trovato [12] un dato molto interessante: se il LLDPE e l’HDPE hanno un MFI simile e comunque minore di 1 le loro proprietà sono molto simili e altrettanto il loro comportamento reologico. Infatti secondo questa teoria il MFI è un fattore reologico molto importante per

(11)

valutare gli effetti di un polimero nelle proprietà e nelle performance del bitume. Assodato questo fatto, siamo andati a vedere se nei lavori con HDPE ci fosse traccia dello strano comportamento notato nella miscela al 4%. In effetti abbiamo trovato un lavoro [15] in cui si verificava esattamente lo stesso fenomeno: ad alte temperature G’(ω) tornava ad essere maggiore di G’’(ω). La spiegazione fornita era che nel range di temperatura in cui il bitume rammollisce si formano piccole microfasi di una fase ricca di polimero, e aumentano le interazioni del polimero: se queste interazioni diventano sufficientemente grandi, la miscela mostrerà proprietà elastiche predominanti, con un valore della loss tangent minore di 1 in un ampio range di frequenze. In effetti questa teoria è confermato dal fatto che anche nel caso della miscela al 4% il secondo crossover si ha proprio nel range di temperatura in cui il bitume rammollisce.

Figura 5-14 Master curve miscela al 4%

1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09

1,E-11 1,E-09 1,E-07 1,E-05 1,E-03 1,E-01 1,E+01 1,E+03

(Pa)

G' G'' tg

La master curve di questa miscela è stata realizzata esattamente come la miscela precedente al 4% e anch’essa, come preventivato presenta due crossover, ma ancora più ravvicinati. Stavolta è chiaro come cada la teoria illustrata precedentemente perché la temperatura di rammollimento di questa miscela è di

(12)

120.5°C, mentre il secondo incrocio si verificato ben prima cioè a circa 60°C. In un successivo lavoro [14] l’autore non cita più infatti la temperatura di rammollimento, ma ipotizza che il maggior valore di G’(ω) rispetto a G’’(ω) e il fatto che entrambe le curve alle basse frequenze vadano verso un plateau sia conseguenza dello sviluppo di una struttura gel dovuta a una più effettiva dispersione del polimero.

Figura 5-15 Master curve miscela al 6%

1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09

1,E-13 1,E-11 1,E-09 1,E-07 1,E-05 1,E-03 1,E-01 1,E+01 1,E+03 1,E+05

(Pa)

G' G'' tg

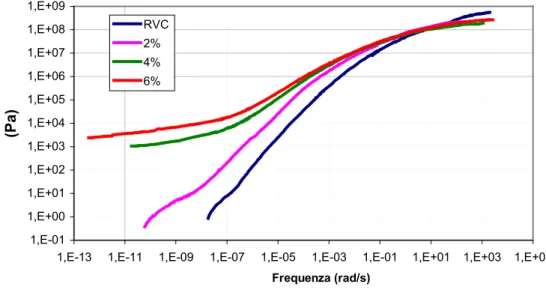
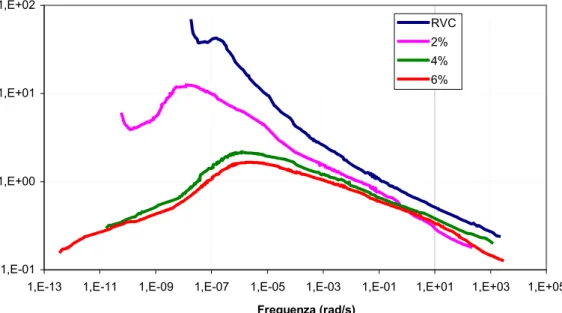
In figura 5-16 si vede come nel caso di G’(ω) con l’aumentare della temperatura si faccia più marcata la differenza tra le 4 curve, con l’aumento di vari ordini di grandezza del G’(ω) all’aumentare della percentuale di polimero. In effetti è noto dalla letteratura che alle basse temperature (alte frequenze) i bitumi modificati con diversa percentuale di polimero abbiano lo stesso comportamento. Inoltre si può notare come se per il bitume tal quale e per la miscela al 2% ci sia una tendenza spiccata verso il basso alle alte temperature, per le miscele al 4% e al 6% la tendenza sia quella di andare verso un plateau.

(13)

Figura 5-16: confronto tra i G’ 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09

1,E-13 1,E-11 1,E-09 1,E-07 1,E-05 1,E-03 1,E-01 1,E+01 1,E+03 1,E+05

(Pa) RVC 2% 4% 6% Frequenza (rad/s)

Per quanto riguarda il G’’(ω) si hanno sempre notevoli incrementi con l’aumentare della temperatura per le miscele rispetto al bitume tal quale, ma questi sono più contenuti. Anche in questo caso per le miscele al 4% e al 6% si ha una diminuzione della pendenza della curva alle alte temperature rispetto al 2% e al bitume.

Figura 5-17: confronto tra i G’’

1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09

1,E-13 1,E-11 1,E-09 1,E-07 1,E-05 1,E-03 1,E-01 1,E+01 1,E+03 1,E+05

(Pa) RVC 2% 4% 6% Frequenza (rad/s)

(14)

Nel grafico delle tangenti si nota chiaramente come le miscele al 4% e al 6% presentino il secondo crossover ossia la tangente a valori della frequenza inferiori a 10-7 rad/s torni ad essere minore di uno, sintomo del passaggio da un comportamento prevalentemente dissipativo ad un comportamento prevalentemente elastico.

Figura 5-18: confronto tra le tg

1,E-01 1,E+00 1,E+01 1,E+02

1,E-13 1,E-11 1,E-09 1,E-07 1,E-05 1,E-03 1,E-01 1,E+01 1,E+03 1,E+05

RVC 2% 4% 6%

5.5 Shift factor ed equazione WLF

I fattori di shift orizzontale necessari per costruire la master curve sono stati interpolati con l’equazione William-Landel-Ferry (2.36) per verificare l’effettiva applicabilità del principio di sovrapposizione. Una buona interpolazione ottenuta con la WLF è infatti indice di un materiale termoreologicamente semplice.

5.5.1 RVC

In figura si riportano i valori sperimentali e le curve ottenute dall’equazione. Gli scostamenti più significativi si presentano alle temperature di 10°C e 20°C. Tali scostamento sono imputabili principalmente ad errori sperimentali nelle misurazioni. Alla temperatura di 20°C è stata variata anche la geometria di misura (barra di torsione→ piatto-piatto).

(15)

Figura 5-19: interpolazione WLF per l’RVC 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09 -30 -20 -10 0 10 20 30 40 50 60 70 log aT shift factor wlf Temperatura (°C)

5.5.2 Miscela bitume - 2% LLDPE

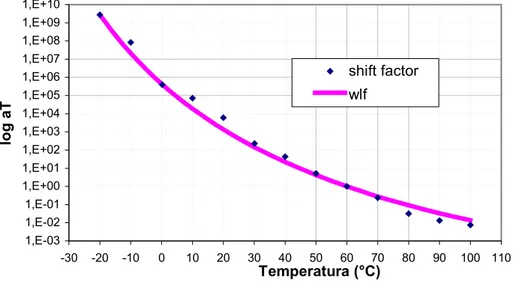
In questo caso gli scostamenti più significativi si hanno per temperature di 10°C, 20°C, 80°C, 90°C e 100°C.

Figura 5-20: interpolazione WLF per la miscela al 2%

1,E-03 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09 1,E+10 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100 110 log aT shift factor wlf Temperatura (°C)

(16)

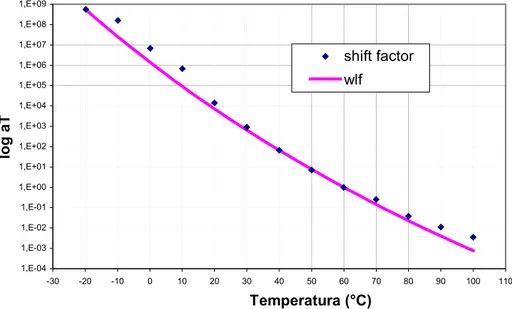
In questo caso gli scostamenti più significativi si hanno per temperature di -10°C, 0°C, 10°C e 100°C. Da segnalare che per le temperature di –20°C, 70°C, 80°C, 90°C e 100°C è stato necessario effettuare oltre a quello orizzontale anche uno shift verticale. Nei capitoli precedenti è stato accennato come lo shift verticale non possa essere modellato da equazioni analitiche perché imputabile a molti fattori (in teoria è dovuto a variazioni di densità) fra i quali in questo caso è possibile annoverare il cambio di geometria.

Figura 5-21: interpolazione WLF per la miscela al 4%

1,E-04 1,E-03 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100 110 log aT shift factor wlf Temperatura (°C)

Gli scostamenti più significativi si hanno per temperature di -20°C, 70°C, 80°C e 100°C. Da segnalare che, come per la miscela al 4%, per le temperature di –20°C, 70°C, 80°C, 90°C e 100°C è stato necessario effettuare oltre a quello orizzontale anche uno shift verticale.

(17)

Figura 5-22: interpolazione WLF per la miscela al 6% 1,E-04 1,E-03 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09 1,E+10 1,E+11 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100 110 log aT shift factor wlf Temperatura (°C)

5.6 Spettri di rilassamento

Con l’utilizzo del software Orchestrator si sono calcolati i tempi di rilassamento ed i relativi valori dello spettro.

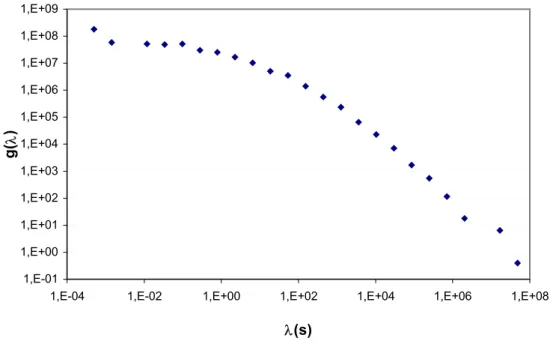
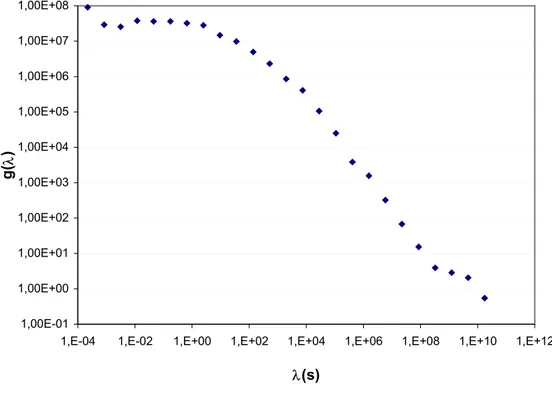
Figura 5-23: Rappresentazione discreta (g) dello spettro di rilassamento H dell’RVC

1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 1,E+09

1,E-04 1,E-02 1,E+00 1,E+02 1,E+04 1,E+06 1,E+08

λ(s)

g(λ

)

(18)

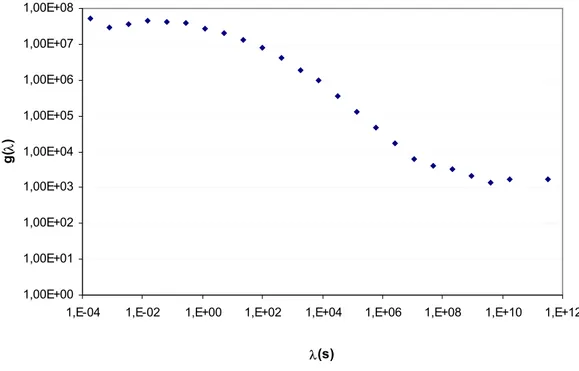
Figura 5-24: Rappresentazione discreta (g) dello spettro di rilassamento H della miscela al 2% 1,00E-01 1,00E+00 1,00E+01 1,00E+02 1,00E+03 1,00E+04 1,00E+05 1,00E+06 1,00E+07 1,00E+08

1,E-04 1,E-02 1,E+00 1,E+02 1,E+04 1,E+06 1,E+08 1,E+10 1,E+12

λ(s)

g(λ

)

Figura 5-25: Rappresentazione discreta (g) dello spettro di rilassamento H della miscela al 4%

1,00E+00 1,00E+01 1,00E+02 1,00E+03 1,00E+04 1,00E+05 1,00E+06 1,00E+07 1,00E+08

1,E-03 1,E-01 1,E+01 1,E+03 1,E+05 1,E+07 1,E+09 1,E+11

λ(s)

g(

(19)

Figura 5-26: Rappresentazione discreta (g) dello spettro di rilassamento H della miscela al 6% 1,00E+00 1,00E+01 1,00E+02 1,00E+03 1,00E+04 1,00E+05 1,00E+06 1,00E+07 1,00E+08

1,E-04 1,E-02 1,E+00 1,E+02 1,E+04 1,E+06 1,E+08 1,E+10 1,E+12

λ(s)

g(λ)

Si vede che gli scostamenti più significativi si hanno per alti valori di λ (cioè di temperatura). Questo deriva (ricordando il modello generalizzato di Maxwell) dal fatto che alle alte temperature (basse frequenze) ci sono le differenze più marcate fra i quattro bitumi. Miscele con alta percentuale di polimero sono più lente a rilassare, cioè hanno modulo più alto anche a basse frequenze (alte temperature). Si vede che occorrerebbe un range molto più ampio per arrivare a gi ≈0.

5.7 Transizione vetrosa

La buona interpolazione ottenuta dall’equazione WLF permette di riportare l’andamento delle proprietà viscoelastiche in funzione della temperatura, ad una data frequenza di riferimento. L’equazione (2.35) si può esprimere in termini logaritmici: ) log( ) log( ) log(ϖ = a_T + ω (5.1)

Fissata una frequenza di riferimento ωrif e sostituendo l’espressione di log(aT) ricavata dalla WLF si ottiene quindi:

(20)

) log( ) ( 1 ) log( ) log( 2 rif r r T T T C T T C a _r ω ϖ + − + − ⋅ + = (5.2)

Dalla quale con pochi passaggi si ricava l’espressione della temperatura in funzione della frequenza ridotta ϖ :

) log( ) log( 1 2 1 2 rif r C C C C T T ω ϖ − + ⋅ + − = _(5.3)

Questo cambio di variabile è particolarmente utile se applicato a G’’(ω); il massimo della funzione G’’(T) visualizza direttamente la temperatura di transizione vetrosa. Nel grafico in Figura 5-12 è riportata G’’(T) a più frequenze di riferimento, per mettere in evidenza che la temperatura di transizione vetrosa è comunque un parametro cinetico ( T=T(ωrif) ).

Figura 5-27: T di transizione vetrosa RVC

0,E+00 2,E+07 4,E+07 6,E+07 8,E+07 1,E+08 1,E+08 1,E+08 2,E+08 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 Temperatura(°C) G''(Pa) f=1Hz f=0,5Hz f=0,1Hz

(21)

Figura 5-28: T di transizione vetrosa miscela al 2% 0,E+00 5,E+06 1,E+07 2,E+07 2,E+07 3,E+07 3,E+07 4,E+07 4,E+07 5,E+07 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 Temperatura (°C) G''(Pa) f= 1Hz f=0,5Hz f=0,1Hz

Figura 5-29: T di transizione vetrosa miscela al 4%

0,E+00 1,E+07 2,E+07 3,E+07 4,E+07 5,E+07 6,E+07 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100 110 120 130 Temperatura(°C) G''(Pa) f=1Hz f=0,5Hz f=0,1Hz

(22)

Figura 5-30: T di transizione vetrosa miscela al 6% 0,E+00 5,E+06 1,E+07 2,E+07 2,E+07 3,E+07 3,E+07 4,E+07 4,E+07 5,E+07 5,E+07 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 Temperatura(°C) G''(Pa) f=1Hz f=0,5Hz f=0,1Hz

5.8 Transizione a liquido viscoso

La transizione del materiale da fluido viscoelastico a fluido prevalentemente viscoso si individua con minore facilità della transizione vetrosa in quanto, specialmente nel caso dei bitumi modificati, avviene a temperature piuttosto alte. Un’indicazione di questa trasformazione si può ottenere dai valori della viscosità complessa. La transizione corrisponde al valore della frequenza alla quale la curva inizia a presentare un asintoto orizzontale. I valori testati delle temperature sono sufficienti a mostrare nel grafico in frequenza l’asintoto per il bitume tal quale e per la miscela al 2% ma per le miscele al 4% e al 6% non sono sufficientemente elevati e l’andamento della viscosità complessa non ha ancora raggiunto il valore di plateau. Questo era un risultato atteso in considerazione della consistenza ancora elevata dei campioni ad alto tenore di polimero.

(23)

Figura 5-31: Viscosità complessa 1,E+00 1,E+03 1,E+06 1,E+09 1,E+12 1,E+15 1,E+18

1,E-13 1,E-11 1,E-09 1,E-07 1,E-05 1,E-03 1,E-01 1,E+01 1,E+03 1,E+05

η * RVC 2% 4% 6% Frequenza (rad/s)

5.9 Misure di viscosità

5.9.1 Modalità delle prove

Le misure di viscosità in regime di scorrimento sono state effettuate con la geometria piatto-piatto su piatti piani da 20 mm di diametro e temperature che variano da 30°C a 70°C. Una possibile fonte di errore nelle misure della viscosità in materiali che presentano una notevole componente elastica è l’irregolarità del flusso conosciuta come “edge fracture” [6] vale a dire una distorsione della superficie libera sul bordo dei piatti durante la rotazione. Questo distorsione di flusso può propagarsi verso l’interno piuttosto velocemente, causando una diminuzione del raggio del campione e quindi errate misurazioni. Tali anomalie di flusso si possono creare anche a shear rate inferiori a quelle alle quali le distorsioni diventano visibili.

(24)

5.9.2 RVC

In figura sono riportate sullo stesso grafico le misure di viscosità a varie temperature in funzione della shear rate ottenute sul bitume tal quale. Dei valori sperimentali è stato fatto un fitting utilizzando due equazioni: la prima proposta da Carreau [23]:

( )

[

]

−p + = 2 01 λγ η η & (5.4)

e la seconda, che non è altro che una modifica della prima, da Yasuda [24]:

( )

[

]

      − + = a n a 1 01 λγ η η & (5.5)

Si può notare come sia presente una viscosità limite, ovvero un plateau per bassi valori dello shear rate, per i quali il fluido ha comportamento Newtoniano.

All’aumentare della shear rate si arriva ad un punto in cui il bitume si discosta dal comportamento Newtoniano e mostra un forte “shear thinning”: il valore della viscosità diminuisce repentinamente. Tanto più elevata è la temperatura e tanto più elevato risulta il valore della shear rate al quale lo shear thinning ha inizio. Come detto, questo andamento è peculiare dei materiali bituminosi, i quali hanno struttura estremamente complessa e sostanzialmente tuttora ignota. Poiché in generale le funzioni reologiche come la viscosità dipendono dalla struttura del materiale, un fenomeno di shear thinning è interpretabile come una “rottura” della struttura preesistente. In altri termini, le tensioni imposte al materiale alterano l’equilibrio del sistema colloidale, eventualmente orientando le micelle asfalteniche e facilitandone lo scorrimento le une rispetto alle altre. Dall’andamento delle curve appare evidente il valore della zero shear rate viscosity per tutte le isoterme.

(25)

Figura 5-32: Viscosità RVC 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05

1,E-04 1,E-03 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03

η (Pa*s) 30°C c 30°C cy 30°C 40°C c 40°C cy 40°C 50°C c 50°C cy 50°C 60°C c 60°C cy 60°C 70°C c 70°C cy 70°C Shear rate (1/s)

Come si può vedere dal grafico, questa miscela presenta lo stesso comportamento del bitume tal quale, rendendo evidente il valore della zero shear rate viscosity per tutte le isoterme. Da notare invece che lo shear thinning è meno evidente.

Figura 5-33: Viscosità miscela al 2%

1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06

1,E-04 1,E-03 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03

(26)

Aumentando la percentuale del polimero, la situazione cambia: diventa difficile individuare il valore della zero shear rate viscosity. Già alle basse frequenze si verifica lo shear thinning, anche se la pendenza della curva non è poi cosi accentuata.

Figura 5-34: Viscosità miscela al 4%

1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06

1,E-03 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02

Qui è ancora più chiaro il comportamento già notato nella miscela 4%. Soprattutto alle alte temperature è quasi impossibile individuare il valore dello zero shear rate viscosity. Già alle basse frequenze si verifica lo shear thinning, infatti si vede una monotona diminuzione della viscosità: ciò comporta anche una deviazione rispetto al fitting di Carreau, a differenza di quello che si era verificato finora, cioè un perfetto fitting dei valori sperimentali. Ancora in letteratura abbiamo trovato una teoria [14] che prova a dare una spiegazione di tale comportamento. Secondo questa teoria, questo comportamento potrebbe essere dovuto alla presenza di forti interazioni tra le microfasi polimeriche. Queste interazioni si dovrebbero essere sviluppate come conseguenza di un processo di rigonfiamento del polimero causato dagli oli maltenici e di un processo di dispersione favorito dall’alta energia fornita dal miscelatore e dalla temperatura di processo.

(27)

Figura 5-35: Viscosità miscela al 6% 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07

1,E-03 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02

In tabella si mostrano i coefficienti utilizzati per il fitting delle curve:

Tabella 5-3: Coefficienti Carreau e Carreau-Yasuda :

Carreau Carreau-Yasuda

RVC

30° 1,21E+02 4,73E-02 9,02E+04 8,48E+00 6,69E-01 7,31E-01 9,22E+04 40° 3,50E+01 3,87E-02 8,84E+03 2,24E+01 8,14E-01 9,06E-01 9,08E+03 50° 2,71E-01 2,20E-01 9,83E+02 9,76E-07 8,11E-01 -4,37E+03 1,01E+03 60° 2,10E-02 8,56E-01 1,90E+02 5,78E-05 1,58E+00 -9,34E+03 1,91E+02 70° 3,98E-05 2,62E+04 1,39E+01 3,70E-04 2,53E+00 -4,15E+03 1,38E+01 2%

30° 2,74E-01 -2,37E-02 1,48E+05 7,59E-01 4,03E+02 1,02E+01 1,47E+05 40° 7,55E+00 4,80E-02 1,84E+04 2,10E+00 1,28E+00 7,40E-01 1,85E+04 50° 6,47E+00 5,00E-02 2,73E+03 3,92E+00 1,03E+00 8,82E-01 2,75E+03 60° 1,61E+00 5,80E-02 5,14E+02 9,90E-13 3,50E-01 -8,59E+02 5,46E+02 70° 1,58E+00 4,30E-02 1,21E+02 9,88E-13 2,30E-01 -2,87E+01 1,38E+02 4%

30° 5,35E+01 1,79E-01 8,75E+05 8,81E+01 2,57E+03 7,70E-01 8,52E+05 40° 1,98E+02 1,17E-01 1,97E+05 2,03E+02 7,23E+02 7,87E-01 1,86E+05 50° 3,92E+01 1,78E-01 4,45E+04 3,63E+01 1,53E+00 6,26E-01 4,57E+04 60° 2,25E+02 1,63E-01 1,42E+04 1,38E+02 3,29E+02 6,79E-01 1,19E+04 70° 1,31E+02 1,30E-01 1,79E+03 1,04E+02 4,63E+01 7,44E-01 1,65E+03 6%

30° 1,06E+02 1,15E-01 9,72E+05 3,93E+00 5,48E-01 2,85E-01 1,09E+06 40° 3,48E+02 1,55E-01 3,47E+05 3,77E+02 9,59E+01 7,15E-01 3,28E+05 50° 3,58E+02 1,87E-01 1,17E+05 3,53E+02 3,73E+00 6,37E-01 1,12E+05 60° 1,06E+03 2,74E-01 7,49E+04 6,67E+02 2,70E+01 4,56E-01 5,69E+04 70° 3,28E+02 3,55E-01 3,73E+04 3,69E+02 5,99E+01 3,59E-01 3,32E+04

(28)

5.10 Prove di stress relaxation

Le prove di stress relaxation sono state effettuate innanzitutto cercando per ogni miscela la temperatura migliore per vedere appunto il rilassamento, poiché a seconda delle temperature scelte, si potevano verificare tre condizioni:

• Il campione rilassava in un tempo brevissimo non rilevabile dallo strumento

• Il campione era troppo deformato e non riusciva più a rilassare

• Il campione rilassava in un tempo sufficientemente lungo da poter essere rilevato dallo strumento

Come spiegato nel capitolo 2, si è trattato, una volta individuata la temperatura opportuna, di applicare vari strain al campione passando da deformazioni piccole (minori dell’1%) nelle quali era lecito attendersi il comportamento lineare, ossia una sovrapposizione delle curve, a deformazioni di maggiore entità (fino al 2% per il bitume tal quale, oltre il 100% per le miscele) a causa delle quali il materiale presentava proprietà viscoelastiche non lineari. Grazie agli shift verticali ci siamo calcolati le varie damping functions e ottenuto le curve G(t,γ) in funzione della shear rate.

5.10.1 Stress relaxation RVC

In figura vengono mostrate le varie curve non shiftate (si può notare la sovrapposizione delle curve con strain bassi 0.35% e 0.5%), le curve shiftate, il fitting delle damping functions (ottenuto col software Table curve), e la definitiva curva G(t,γ).

(29)

Figura 5-36: Stress relaxation RVC curve non shiftate 1,E+04 1,E+05 1,E+06 1,E+07 1,E+08 7 17 27 37 47 57 67 77 87 Tempo (s) G (t) (Pa) 0.35 0.5 0.8 1.1 1.3 1.5 2

Figura 5-37: Stress relaxation RVC curve shiftate

1,E+04 1,E+05 1,E+06 1,E+07 7 17 27 37 47 57 67 77 87 tempo (s) G (t) (Pa) 0.35 0,5 0.8 1.1 1,3 1.5 2

(30)

Figura 5-38: Damping function RVC 0,1 1 10 0,1 1 γ 10 h(γ) valori di shift Soskey & Winter Osaki

Zapas

La curva che esegue il miglior fitting dei valori di shift è quella proposta da Soskey e Winter, con parametri a=0.909 e b=3.023.

Figura 5-39: Stress relaxation RVC con l’uso della damping function

5.10.2 Stress relaxation miscela al 2%

Una volta mostrato il procedimento utilizzato, per comodità mostriamo d’ora in poi solo le damping functions e la curva G(t,γ).

1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 0 50 100 150 200 250 300 350 400 tempo (s) G(t)h (γ ) (Pa) 0,35 0,5 0,8 1,1 1,3 1,5 2

(31)

Figura 5-40: Damping function miscela al 2% 0,1 1 0,1 1 10 100 γ h(γ) valori di shift Osaki Zapas

Soskey & Winter

La curva che esegue il miglior fitting dei valori di shift è quella proposta da Osaki, con parametri a=0.035, b=100 e c=1.

Figura 5-41: Stress relaxation miscela al 2% con l’uso della damping function

1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 0 100 200 300 400 500 600 700 800 900 tempo(s) G (t)h( γ ) (Pa) 0,5 1 5 10 20 25 30 50

(32)

Figura 5-42: Damping function miscela al 4%

0,01 0,1 1 1 10 100 1000 γ h(γ) valori di shift Osaki Zapas

Soskey & Winter

La curva che esegue il miglior fitting dei valori di shift è quella proposta da Osaki, con parametri a=0.07749, b=0.1356 e c=0.2639.

1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 0 100 200 300 400 500 600 700 800 900 tempo(s) G (t)h( γ) (Pa) 1 2 10 20 35 100 250

(33)

Figura 5-44: Damping function miscela al 6%

0,0001 0,001 0,01 0,1 1 0,1 1 10 100 1000 γ h(γ) valori di shift Osaki Zapas

Soskey & Winter

La curva che esegue il miglior fitting dei valori di shift è quella proposta da Osaki, con parametri a=0.02601, b=0.5076 e c=0.5741.

1,00E+00 1,00E+01 1,00E+02 1,00E+03 1,00E+04 1,00E+05 1,00E+06 0 100 200 300 400 500 600 700 800 900 tempo (s) G(t)h( γ) (Pa) 0,1 0,6 0,8 2 3,5 8 12 20 35 80 100 200