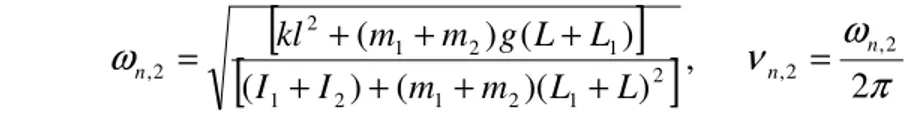PARTE TERZA: I Moti di Whirl in GGGPARTE TERZA: I Moti di Whirl in GGGPARTE TERZA: I Moti di Whirl in GGGPARTE TERZA: I Moti di Whirl in GGG

PARTE TERZA: I Moti di Whirl in GGG

PARTE TERZA: I Moti di Whirl in GGG

PARTE TERZA: I Moti di Whirl in GGG

PARTE TERZA: I Moti di Whirl in GGG

In questo capitolo applicheremo gli elementi di dinamica dei rotori visti precedentemente per analizzare il comportamento dinamico di GGG e cercare di controllare i moti di whirl presenti nell’esperimento. Come abbiamo visto nelle parti precedenti l’apparato di GGG è composto essenzialmente da due cilindri concentrici e rotanti, accoppiati fra di loro grazie ad un braccio di accoppiamento e delle sospensioni laminari di costante elastica molto bassa. Poichè l’esperimento è terrestre e non spaziale, la rotazione deve essere assicurata da un motore e da un albero di trasmissione che trasmette tale rotazione al braccio di accoppiamento e da lì ai cilindri. L’obiettivo che GGG si propone è molto ambizioso e richiede una notevole accuratezza nella modellizzazione. Come è lecito aspettarsi in questi casi, il modello teorico necessario per avere un buon accordo con i risultati sperimentali è troppo complesso per avere delle soluzioni analitiche esplicite che siano presentabili e intelleggibili. Il modello teorico realistico –che sarà oggetto del terzo paragrafo di questo capitolo- verrà integrato numericamente con il programma MatLab, per cui non verranno fornite soluzioni analitiche esplicite per tale modello. Per permettere una comprensione intuitiva di alcuni fenomeni fondamentali –precedentemente spiegati in modo generico nella prima parte della Tesi- abbiamo allora deciso di premettere al modello teorico realistico, una serie di modelli matematici molto semplificati che, nei limiti degli argomenti trattati hanno un accordo sia qualitativo che quantitativo con i dati sperimentali. Questi modelli permetteranno di comprendere meglio alcuni valori provenienti dai dati sperimentali. Poichè questi modelli sono essenzialmente euristici con fini propedeutici a comprendere il funzionamento intuitivo dell’apparato (lasciando al modello realistico il compito di descriverlo rigorosamente) abbiamo preferito, ove possibile ed entro certi ragionevoli limiti, scegliere un approccio meno rigoroso ma che permettesse di comprendere più approfonditamente il comportamento qualitativo dell’apparato.

I. Modelli Matematici di GGG

I. Modelli Matematici di GGG

I. Modelli Matematici di GGG

I. Modelli Matematici di GGG

1. Modello semplificato per le frequenze naturali 1. Modello semplificato per le frequenze naturali 1. Modello semplificato per le frequenze naturali 1. Modello semplificato per le frequenze naturali

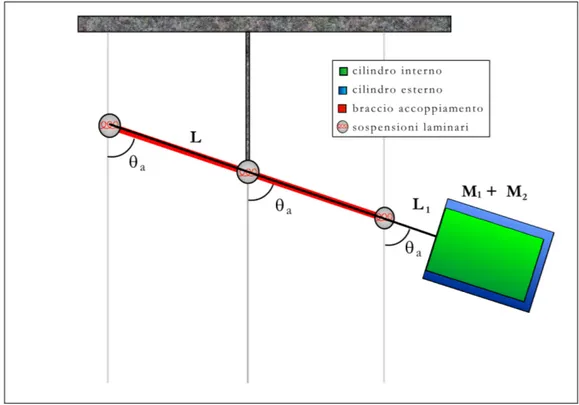
In questo paragrafo struttureremo un modello che sia capace di determinare le frequenze naturali del sistema privo di rotazione. Per tale scopo considerremo il modello matematico rappresentato in figura 1.

fig III.1: modello matematico semplificato per la determinazione dei modi normali di GGG Chiamiamo gli angoli θλ (λ=a,1,2) gli angoli che separano rispettivamente il braccio

di accoppiamento, il cilindro interno e il cilindro esterno dalla verticale locale. Qualitativamente la presenza di tre corpi (due uguali e uno diverso) accoppiati con tre molle ideali uguali lascia supporre l’esistenza di tre frequenze naturali fondamentali: la prima che corrisponde alla configurazione in cui il cilindro interno e il cilindro esterno oscillano senza inclinarsi rispetto alla verticale (i.e. θλ =0∀λ∈

{ }

1,2 ) ovvero in controfase rispetto al braccio di accoppiamento, la seconda in cui i due cilindri sospesi oscillano in fase con il braccio di accoppiamento (i.e.

{

a,1,2

}

a∀ ∈

=θ λ

θλ ) e la terza in cui uno dei due oscilla in fase e l’altro in controfase con il braccio di accoppiamento (i.e. θ1=−αθ_a, θ2 =(1−α)θ_a con α da determinare).

Nominalmente questi tre casi corrispondono rispettivamente ad un modo differenziale e a due modi comuni di GGG [24]. Adesso determineremo le frequenze naturali relative a queste oscillazioni.

Per tale scopo prenderemo in considerazione la modellizzazione in figura 2, prima considerando come le se braccia di accoppiamento fossero perfettamente bilanciate e successivamente invece prenderemo in considerazione anche l’ipotesi di uno sbilanciamento del punto di sospensione rispetto all’asse di simmetria del braccio di accoppiamento pari a ∆L. La prima modellizzazione è utile per determinare qualitativamente le frequenze di risonanza dell’esperimento, la seconda per capire come ∆L possa essere utilizzato per modificare il periodo di oscillazione naturale del sistema.

fig III.2: modello matematico semplificato per la determinazione del modo differenziale di GGG Ponendo θλ =0∀λ∈

{ }

1,2 , trascurando per il momento ∆L e chiamando l la massima estensione delle sospensioni laminari abbiamo che l’energia potenziale è data da:

(1) U

(

ka k k

)

l

θ

a 2 2 2 1 sin 2 1 + + =

mentre l’energia cinetica del sistema risulta essere

(2) 2 2 2 2 1 ] [ 2 1 a L m L m T = + θ&

(3) m L m L θa

(

ka k k

)

l θa 2 2 2 1 2 2 2 2 1 sin 2 1 ] [ 2 1 + + − + = & L

Nei limiti delle piccole oscillazioni in cui sin

θ

a ≈

θ

atroviamo immediatamente le equazioni del moto che sono

(4) m m L

θ

a

(

ka k k

)

l

θ

a 2 2 1 2 2 1 ) ] [( + && = + +

ovvero la frequenza naturale del sistema che risulta essere

(5)

(

)

m k L l L m m l k k ka a 2 3 ] ) [( 1 2 2 2 2 1 = + + + =

ω

Che ha una forma molto naturale per un’oscillatore armonico. Raffinando appena il modello possiamo ora introdurre anche lo sbilanciamento ∆L del braccio di accoppiamento. Supponendo che tale sbilanciamento sia diretto a favore della parte relativa al cilindro esterno, questo si traduce nell’aggiungere un termine nell’energia potenziale pari a: (6) ) 2 sin 2 1 ( cos 2 2 2 a a L m Lg m Lg U_∆ = ∆

θ

= ∆ −

θ

Quindi, a meno di costanti, e considerando l’approssimazione delle piccole oscillazioni, abbiamo che l’energia potenziale può essere scritta come

(7)

(

(

)

2

)

2 2 2 1 2 1 ' U U _L k_a k k l m Lg _a U = + ∆ ≈ + + + ∆

θ

Similmente l’energia cinetica diventa

(8) 2 2 2 2 1 ( ) ] [ 2 1 a L L m L m T = + +∆

θ

&

E derivando le equazioni del moto si ottiene una frequenza naturale pari a

(9)

(

)

_{2 2} 2 1 2 2 1 1 , 2 ] ) [( L L g L m m l k k ka n ∆ − + + + =

ω

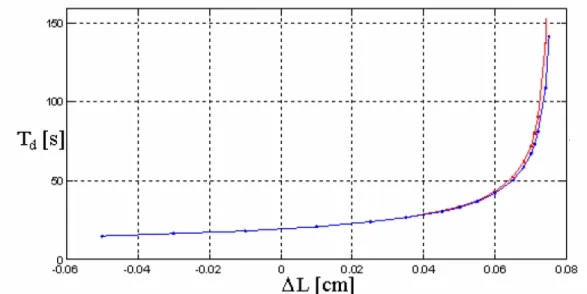
Ponendo all’interno di questa equazione i valori realistici dei parametri come sono sintetizzati nelle tabelle relative del paragrafo 4 si ottiene una stima quasi perfetta della frequenza naturale del sistema non rotante in funzione di ∆L. Il valore operativo della frequenza in questione (

π ω ν 2 1 , 1 , n n = ) è circa 0.09 Hz, ma come

evidenziato dalla formula, tale valore può essere spostato modificando artificialmente il parametro ∆L (grazie all’utilizzo di piezoceramiche che spostano il braccio di accoppiamento). Il grafico sottoriportato illustra la dipendenza del periodo di oscillazione naturale in funzione dello spostamento ∆L (linea rossa dati sperimentali, linea blu calcoli teorici con la formula soprariportata).

fig III.3: periodo differenziale in funzione di ∆ L

Per trovare la seconda frequenza naturale poniamo adesso θλ =θ_a∀λ∈

{

a,1,2

}

. La condizione corrisponde al caso in cui i tre corpi oscillano in fase fra di loro come da figura 4

fig III.4: modello matematico semplificato per la determinazione del primo modo comune di GGG

Poichè i cilindri oscillano in fase con il braccio di accoppiamento, l’unica sospensione che si deforma richiamando i corpi è la sospensione centrale. Se scriviamo l’energia potenziale utilizzando la solita approssimazione per le piccole oscillazioni otteniamo:

(10)

[

1 2 1

]

2 2 1 2 1 2

)

(

)

(

2

1

cos

)

(

)

(

sin

2

1

a a a

m

m

g

L

L

kl

m

m

g

L

L

kl

U

=

θ

+

+

+

θ

≈

+

+

+

θ

e come energia cinetica:

(11)

[

( 1 2) ( 1 2)( 1 )2

]

2 2 1 a L L m m I I T = + + + +

θ

&

Da cui l’equazione del moto:

[

]

[

]

a a a a I I m m L L L L g m m kl U T dt d

θ

θ

θ

θ

2 1 2 1 2 1 1 2 1 2 ) )( ( ) ( ) ( ) ( + + + + + + + = ⇒ ∂ ∂ = ∂ ∂ _&& &

(12)

[

]

[

]

π

ω

ν

ω

2 , ) )( ( ) ( ) ( ) ( ,2 2 , 2 1 2 1 2 1 1 2 1 2 2 , n n n L L m m I I L L g m m kl = + + + + + + + =

E il suo valore numerico è ν_n,2 = 0.94 Hz, che è ancora in buon accordo con il valore sperimentale pari a 0.91 Hz.

fig III.5: modello matematico semplificato per la determinazione del secondo modo comune di GGG

Per calcolare la terza frequenza di risonanza, invece, dobbiamo fare delle ipotesi aggiuntive: dobbiamo calcolare gli angoli θ1, θ2corrispondenti ad una oscillazione in controfase dei due cilindri. Supporremo come prima cosa che tali angoli dipendano linearmente dall’angolo di incinazione del braccio di accoppiamento, cioè

a

a θ α θ

αθ

θ1 =− , 2 =(1− )

Per determinare poi quantitativamente α imporremo che il centro di massa dei due cilindri debba coincidere fra di loro cioè chiederemo che

(13) Lsin((1−

α

)

θ

_a)−Lsin

θ

_a =Lsin

θ

_a +Lsin(−

αθ

_a)

(14) L(1− )

α

θ

a −L

θ

a ≈L

θ

a −L

αθ

a

Come si può notare qui abbiamo già fatto un’approssimazione solo parzialmente giustificata, la vera giustificazione di tale approssimazione risiede nel fatto che stiamo facendo semplicemente delle stime del tutto qualitative e non siamo al momento interessati a trovare i valori precisi di tali frequenze, ma solo dei valori approssimativi che ci permettano di comprendere meglio il comportamento del modello reale. Ripercorrendo nuovamente i passaggi per l’energia potenziale e per l’energia cinetica, abbiamo:

(

k k k

)

l mL mL g

U asin a sin ( a) sin ((1 ) a) ( cos( a) cos((1 ) a))

2 1 1 1 1 1 2 2 2 2 1 2 θ α αθ θ α αθ θ + − + − + − + − =

Ovvero con le solite approssimazioni per angoli piccoli

(15)

(

(

)

1 1 2

)

2 2 1 1 2 2 2 1 2

)

)

1

(

(

)

1

(

2

1

a a

k

k

l

m

L

m

L

g

k

U

≈

+

+

α

+

α

+

α

+

−

α

θ

E per l’energia cinetica

(16)

(

2 2 2

)

2 2 1 1 2 2 1 2

)

)

1

(

(

)

(

)

1

(

2

1

a

L

L

m

L

L

m

I

I

T

≈

α

+

−

α

+

−

α

+

−

α

−

θ

&

Per cui, in definitiva abbiamo per queste oscillazioni una frequenza naturale data da

(17)

[

(

)

]

[

]

π

ω

ν

α

α

α

α

α

α

α

α

ω

2 , ) ) 1 ( ( ) ( ) 1 ( ) ) 1 ( ( ) 1 ( ,3 3 , 2 2 2 2 1 1 2 2 1 2 2 1 1 2 1 1 2 2 2 1 2 3 , n n a n L L m L L m I I g L m L m l k k k = − − + − + − + − + + + + + =

E il suo valore numerico è ν_n,3 = 1.01 Hz, mentre il suo valore sperimentale è pari a 1.26 Hz.

Questo semplice modello matematico è ovviamente del tutto insufficiente per rendere conto del comportamento dinamico dell’apparato GGG, ma è utile perchè fornisce una comprensione intuitiva di alcuni fatti che risulteranno utili in seguito. Riassumendo il paragrafo, nel caso ideale di sospensioni ideali in GGG, che non hanno dunque dispersione di energia, e che sono isotrope, il modello appena proposto ci dice che:

1. Il sistema ha 3 frequenze naturali

2. Solo una di queste frequenze ω_n,1 dipende da ∆L e quindi può essere cambiata con una diversa calibratura del sistema

3. Le tre frequenze di risonanza hanno valori approssimativi di 0.09 Hz, 0.94 Hz, 1.01 Hz

Combinando queste informazioni con ciò che sappiamo di teoria di dinamica dei rotori, possiamo, inoltre, fare delle previsioni sul modello reale che tiene di conto dell’anisotropia delle molle e delle loro fattore di qualità limitato. Le nostre aspettative sulle frequenze naturali saranno , in particolare:

(Effetti dovuti alla dispersione energetica)

1. La dispersione energetica delle molle non deve cambiare radicalmente i valori delle frequenze naturali principali, ma solo l’ampiezza dei moti

(Effetti dovuti all’anisotropia delle molle)

1. Ci aspettiamo che ogni frequenza naturale si divida in due frequenze naturali distinte e ravvicinate

_n,i →Λ≠0 _n−_,i, _n+_,i con _n+_,i = Λ _n−_,i ∀i∈

{

a,1,2

}

ω ω ω ω ω

2. Che

ω

n+,isia dipendente dalla velocità di rotazione del sistema mentre ω_n−_,i ≈ω_{n,i rimanga sostanzialmente costante e dunque}

che le tre frequenze principali trovate siano più o meno sempre presenti indipendentemente dalla velocità di rotazione del sistema

3. Ci aspettiamo inoltre che questa anisotropia dia origine a delle regioni di instabilità situate in un intorno ωs ≈ωn,i la cui ampiezza sia di circa ∆ω =1− Λ

2. Modello semplificato per l’autocentratura 2. Modello semplificato per l’autocentratura 2. Modello semplificato per l’autocentratura 2. Modello semplificato per l’autocentratura

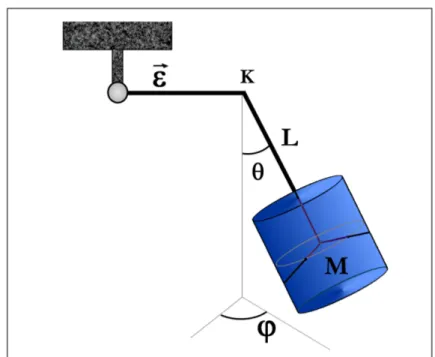
Il modello presentato in questo paragrafo permette di comprendere il meccanismo dell’autocentratura che è stato presentato nel capitolo precedente, facendo vedere come tale meccanismo sia presente anche in un sistema affine a GGG.

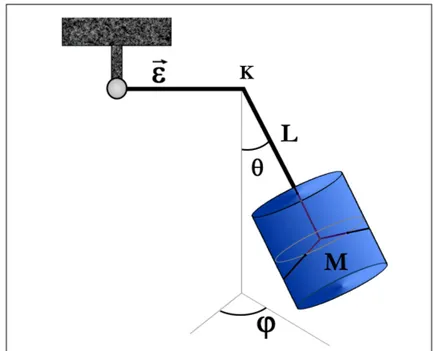
fig III.5: modello matematico semplificato per la l’autocentratura di GGG

Nel modello in questione, prendiamo in considerazione un singolo cilindro rotante M, sospeso ad una distanza L dal punto K, mediante una sospensione laminare con costante elatica non isotropica (kξ=k, kη=Λk) di lunghezza l. L’eccentricità è rappresentata dal vettore ε che parte dall’albero di trasmissione diretto vero il punto K. Tutto il sistema ha due gradi di libertà e quindi può essere studiato con l’inserimento di due variabili angolo θ e ϕ che rappresentano rispettivamente, l’angolo del braccio rispetto alla verticale locale e l’angolo del braccio rispetto all’asse ξ del

riferimento rotante (O,ξ,η,z).

Chiameremo inoltre (O,Γ,Ξ,Η) il sistema di riferimento in cui il cilindro è fisso, con assi coincidenti con gli assi di inerzia principali.

Per trovare la Lagrangiana di questo sistema, svilupperemo una formula di carattere del tutto generale che sarà fondamentale in seguito per lo sviluppo del modello reale di GGG e che per questo preferiamo sviluppare in un caso semplificato in cui è presente solo un cilindro rotante in un sistema di riferimento rotante. Per fare questo, procederemo per gradi, in primo luogo sarà necessario scrivere in una forma operativa la funzione Langrangiana nelle coordinate di un sistema di riferimento rotante [25].

La Lagrangiana di un corpo rigido in un sistema di riferimento inerziale fisso può essere scritta nella forma:

(1) =

∫

v_nr2dm−U

2 1 r L

Dove v_nr è che la velocità dell’elemento di massa dm del corpo rigido letta nel sistema di riferimento fisso (O,x,y,z) e U l’energia potenziale del sistema.

Se vogliamo leggere questa velocità in un sistema di riferimento rotante (O,ξ,ν,ζ) rispetto al primo con una velocità angolare ω_s (notare che l’origine dei due riferimenti è coincidente), chiamando r il vettore posizione dell’elemento di massa dm, allora la velocità v_nr diventa (2) vnr =v + ×r ⇒ =

∫

v + ×r dm−U 2 ( ( 2 1 (

ω

s ) L _ξηζ

ω

s )) ξηζ r r r

Dove vr_ξηζ rappresenta la velocità dell’elemento di massa dm letta nel sistema di riferimento rotante e che d’ora in avanti indicheremo semplicemente con il termine

vr . Espandendo i termini della Lagrangiana otteniamo la formula della Lagrangiana per un sistema di riferimento rotante:

(3) =

∫

v2dm+

∫

v⋅ ×r dm+

∫

×r 2dm−U ( 2 1 ( 2 1 ) ) L r r

ω

s

ω

s

b. La Lagrangiana di un cilindro rotante in un sistema di riferimento rotante

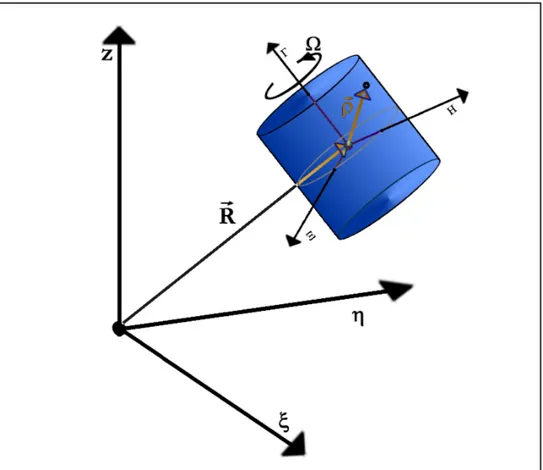
Ora invece consideriamo un cilindro che nel sistema di riferimento ruotante ruoti attorno ad un proprio asse principale di inerzia coincidente con Γ (nel riferimento in cui il cilindro è fisso) e con momenti principali di inerzia pari a IΓ, IΞ, IΗ=IΞ.

Chiamiamo Ω la velocità angolare del corpo rispetto al riferimento rotante e calcoliamo i termini della Lagrangiana per tale corpo

fig III.6: cilindro che ruota in un sistema di riferimento rotante

In tale sistema di riferimento la Lagrangiana può essere scritta in questa forma

(4) =

∫

v2dm+

∫

v⋅ ×r dm+

∫

×r 2dm−U ( 2 1 ( 2 1 ) ) L r r

ω

s

ω

s

dove v rappresenta la velocità dell’elemento di massa dm letta nel sistema di riferimento(O,ξ,ν,z). Se chiamiamo Ω la velocità angolare del corpo nel sistema di riferimento(O,ξ,ν,z), R il vettore indicante il centro di massa del cilindro, V la velocità del centro di massa del cilindro, e chiamiamo ρ la distanza dell’elemento di massa dm dal centro di massa del cilindro, allora

(5) v =V +Ω×

ρ

, r = R+

ρ

Sostituendo nella Lagrangiana, questa diventa:

(

V +Ω×

)

dm+

(

V +Ω×

)

⋅ ×

(

R+

)

dm+ ×

(

R+

)

dm−U =

∫

∫

∫

4 4 3 4 4 2 1 4 4 4 4 4 3 4 4 4 4 4 2 1 4 4 3 4 4 2 1 centr Cor k U s V s T ) ) L 2 2 ( 2 1 ( 2 1

ρ

ω

ρ

ω

ρ

ρ

Nella formula precedente abbiamo assegnato dei nomi per indicare i termini principali della Lagrangiana. Al primo abbiamo dato T_k per indicare che il termine è

composto solo da velocità, al secondo abbiamo dato il nome V_cor per indicare che esso risulterà dipendente sia dalle coordinate generalizzate che dalle loro derivate temporali e l’ultimo l’abbiamo indicato come Ucentr per indicare che il termine risulterà solo funzione delle coordinate generalizzate.

Ora consideriamo i termini della Lagrangiana in modo separato

(6) =

∫

(

V +Ω×

)

2dm=

∫

V2dm+

∫

(

V⋅

(

Ω×

)

)

dm+

∫

(

Ω×

)

2dm 2 1 2 1 2 1

ρ

ρ

ρ

k T

Per le proprietà del centro di massa il termine centrale di questa espressione si annulla (7)

∫

(

⋅

(

Ω×

)

)

= ⋅

∫

(

Ω×

)

=

(

×Ω

)

⋅

∫

∫ dm=0→0 dm V dm V dm V

ρ

ρ

ρ

ρ

Per cui Tk diventa

(8) 2 2 2 1 2 1 α α ααΩ + = MV

∑

I k T

Il secondo termine della Lagrangiana è:

(

)

(

)

(

)

R dm

(

)

dm dm V dm R V dm R V

∫

∫

∫

∫

∫

× ⋅ × Ω + × ⋅ × Ω + × ⋅ + × ⋅ = = + × ⋅ × Ω + = ) ) ) ) ) V s s s s s Cor

ρ

ω

ρ

ω

ρ

ρ

ω

ω

ρ

ω

ρ

( ( ( ( (

Sempre per la definizione di centro di massa

∫

ρ

dm=0 procedendo in modo analogo a come fatto precedentemente, il secondo ed il terzo termine si annullano lasciando

(9) V_Cor =MV ⋅(

ω

s×R)+

∫

(

Ω×

ρ

)

⋅(

ω

s×

ρ

)dm

Allo stesso modo il terzo termine della Lagrangiana può essere semplificato

(

R

)

dm

∫

R dm

∫

R dm

∫

dm

∫

× + = × + × ⋅ × + × = 2 2 2 ( 2 1 ( ( ( 2 1 ( 2 1 ) ) ) ) ) U_Centr

ω

s

ρ

ω

s

ω

s

ω

s

ρ

ω

s

ρ

E con il solito procedimento

0 ( ( ( ( × ⋅ × = × ⋅

∫

× =

∫

ω

s R)

ω

s

ρ

)dm

ω

s R)

ω

s

ρ

)dm

(10) = M ×R 2 +

∫

× 2dm ( 2 1 ( 2 1 ) ) U_Centr

ω

s

ω

s

ρ

Dunque la Lagrangiana del cilindro rotante nel sistema di riferimento ruotante può essere scritta come la somma dei quattro termini fondamentali che abbiamo trovato cioè:

(11) L=Tk+VCor +UCentr −U con U che rappresenta l’energia potenziale e

(12) 2 2 2 1 2 1 α α ααΩ + = MV

∑

I k T (13) V_Cor =MV ⋅(

ω

s×R)+

∫

(

Ω×

ρ

)

⋅(

ω

s×

ρ

)dm (14) = M ×R 2 +

∫

× 2dm ( 2 1 ( 2 1 ) ) U_Centr

ω

s

ω

s

ρ

Questa è una formula di carattere generale che utilizzeremo anche per il modello reale di GGG.

fig III.5: modello matematico semplificato per la l’autocentratura di GGG

A questo punto possiamo applicare la formula della Lagrangiana nel nostro caso particolare per studiare l’effetto di autocentratura per un cilindro di massa M.

Abbiamo visto che la Lagrangiana di tale sistema è data dalla somma di quattro termini di cui abbiamo trovato le espressioni nelle coordinate (O,ξ,η,z)

Ora risulta necessario scrivere tali termini in funzione delle due coordinate generalizzate ϕe θ. Per fare questo dobbiamo considerare le seguenti relazioni:

(14)      − = + = + =

θ

φ

θ

ε

η

φ

θ

ε

ξ

cos sin sin cos sin L z L L

e tradurre dunque i termini che sono scritti in funzione di ξ,η,z in funzione di ϕ e θ. Per fare questo avremo anche bisogno di conoscere le funzioni in ϕ e θ di Ω e ρ lette nel riferimento rotante. Per fare questo basta notare che esse possono essere trovate in modo più semplice nel riferimento in cui il cilindro è fisso (O,Γ,Ξ,Η), applicando poi la rotazione M di passaggio fra i due riferimenti che è data da

(15)           − − − = Ω = Ω ΞΗΓ

θ

θ

φ

θ

φ

θ

φ

φ

θ

φ

θ

φ

cos sin 0 sin sin sin cos cos cos sin cos cos sin , M M (16)             − = ΩΞΗΓ s

ω

θ

φ

θ

sin & &

Sostituendo queste relazioni nei vari termini trovati nella Lagrangiana otteniamo le seguenti espressioni: ) sin )( ( 2 1 2 2 2 2 θ θ φ& + & + = ML I_Ξ k T

[

]

{

φ

θ

ε

θ

θ

φ

φ

φ

θ

}

ω

φ

θ

ω

θ

ω

L2 sin2 L cos sin cos sin I _s sin2 I _s2cos

M + + + _Ξ + _Γ

= s & & & &

Cor V

[

θ

ε

θ

φ

]

ω

θ

ω

2 2 2 2 sin ) ( 2 1 cos sin 2 sin 2 1 s sLL I I M + + _Ξ − _Γ = Centr U

A questi termini va aggiunto il potenziale scritto in coordinate generalizzate che è formato da una componente gravitazionale e una componente elastica (per la quale supponiamo anche un’anisotropia Λ):

(17)

θ

2 2

θ

(

2

φ

2

φ

)

sin cos sin 2 1 cos + +Λ − = mgL kl U

La Lagrangiana definitiva è data da

(18) L(

θ

,

φ

,

θ

&,

φ

&) =T_k +V_Cor +U_Centr −U Se vogliamo considerare le posizioni di equilibrio

(19) ⇒ =I _s + −U     = = Γ UCentr ) , , , L(

θ

φ

ω

θ

φ

θ

cos 0 0 0 0 ₂ & &

Le equazioni di equilibrio sono determinate dalle condizioni:

(20)       = ∂ ∂ = ∂ ∂ 0 0 0 0 0 0 0 0 0 0 , , φ θ φ θ

φ

φ

θ

θ

φ

θ

) , , , L( ) , , , L(

Ovvero svolgendo i calcoli, tenendo di conto che 2sinθcosθ=sin2θ,

(21)

[

]

(

)

         = Λ − + − = Λ + − − − + + + − Γ Ξ Γ 0 2 sin sin ) 1 ( 2 1 ) sin sin 2 ( 2 1 0 sin cos 2 sin 2 1 sin 2 sin ) ( 2 1 cos cos 2 2 sin 2 1 sin 2 2 2 2 2 2 2 2 2

φ

θ

φ

θ

ε

ω

φ

φ

θ

θ

θ

ω

φ

θ

ε

θ

ω

θ

ω

l k L M kl MgL I I L L M I s s s s

Con l’approssimazione dei piccoli angoli le equazioni diventano

(22)

[

]

(

)

(

)

    = Λ − + − = Λ + − − − + − − + _{Ξ Γ} 0 ) 1 ( 0 1 ) 2 ( ) 2 1 )( 2 1 ( 2 2 2 2 2 2 2 2 2

φ

θ

εθ

ω

φ

θ

θ

θ

ω

φ

θ

ε

θ

ω

l k L M kl MgL I I L L M s s s

E le soluzioni di di questo sistema sono date da

(23)        =       + − − + = Γ Ξ

π

φ

ω

ε

ω

θ

, 0 ) 2 ( 2 , 1 2 , 1 0 2 2 2 2 2 2 0 ML kl L g ML I I ML L M s s m

Per commentare questa soluzione conviene scriverla in un modo più significativo. Per farlo chiamiamo L’ lunghezza effettiva e ω_n la frequenza naturale così definite:

      +  ← − +  ← Ξ Γ 2 2 2 2 ( 2 ) ' ML kl L g M I I L L

ω

n

(24)       − = − = 2 2 2 2 2 2 2 2 2 2 0 ' ' 2 , 1 n s s n s s L L L L L L

ω

ω

ω

ε

ω

ω

ε

ω

θ

m m Considerando che (25)               −       − = ± ≅ ∆ 2 2 2 2 2 0 ' 1 n s s L L L

ω

ω

ω

ε

θ

ε

ξ

Possiamo facilmente riscontrare alcune analogie con il modello elementare di rotore analizzato nel capitolo precedente. Come prima cosa, notiamo che nel limite L’=L otteniamo una formula equivalente a quella ottenuta per il rotore elementare.

      − − ≅ ∆       →  − + = Ξ Γ − Ξ− Γ → 2 2 2 0 ) 2 ( 2 2 1 ) 2 ( ' 1 n s s I I M M I I L L ω ω ω ε ξ

Per cui incorriamo nel classico fenomeno di autocentratura per velocità supercritiche (come è stato trattato nel capitolo precedente).

Viceversa in assenza di applicabilità di questo limite

      ₋ ≅ ∆    →                − − ≅ ∆ →∞ − 2 2 2 1 2 2 2 2 ' ' ' 1 L L L L L _s s n

_ξ

_ε

ω

ω

ε

ξ

ω

Ovvero lo sfasamento con il crescere arbitrario della velocità di rotazione, tende ad una certa costante dipendente dalle caratteristiche fisico-geometriche del corpo cioè

(26) _      − + − ≅ ∆ Γ Ξ Γ Ξ )) 2 ( ( ) 2 ( 2 I I ML I I

ε

ξ

Il punto di minimo sfasamento è invece ottenuto nel caso in cui

(27) ' ₂ 1 2 2 2 =       − s n L L

ω

ω

ovvero nel momento in cui la velocità di rotazione assume il valore (28) _      − = _{2 2} 2 2 2 ' L L L n s

ω

ω

A questa particolare velocità di rotazione l’autocentratura risulta essere la massima possibile e virtualmente perfetta. Il modello qui presentato potrebbe essere ulteriormente complicato introducendo un ulteriore errore nel posizionamento del cilindro rispetto all’asse L come nella figura sottostante, per essere più aderente al caso reale in cui incorre anche un errore nel posizionamento della massa test. Una modellizzazione per questo caso potrebbe essere quella rappresentata in figura. Tuttavia l’aggiunta di questo ulteriore errore di posizionamento ε2 risulta, in definitiva, essere ininfluente sul comportamento qualitativo del sistema [14]. A titolo di esempio riportiamo la simulazione del comportamento dei vari rotori modellizzati (punto materiale, cilindro con offset e cilindro con due offset).

fig III.7: risultati teorici e confronti sperimentali relativi all’autocentratura di GGG

Come è possibile notare dalla figura l’aggiunta di un errore aggiuntivo nel posizionamento del cilindro non cambia l’andamento qualitativo del sistema. Al lato del grafico principale si può vedere il grafico riguardante la risposta dinamica di GGG all’autocentratura risultante da una simulazione sul modello reale di GGG. Questa similitudine di diagrammi conferma la sostanziale adeguatezza del modello semplificato nel descrivere qualitativamente il fenomeno. Riassumendo, lo studio di questo modello semplificato per uno studio qualitativo relativo all’autocentratura di GGG evidenzia che:

1. Il fenomeno dell’autocentratura supercritica è presente anche nei cilindri di GGG

2. Mentre nel rotore elementare visto nel capitolo 3, l’autocentratura era massima con ωs→∞, in questo caso

dovremo aspettarci un’autocentratura massima ad una velocità di rotazione dettata dalla condizione

_











−

=

_{2 2} 2 2 2

'

L

L

L

n s

ω

ω

.

3. Nel caso ωs →∞avremo invece 

     − + − ≅ ∆ Γ Ξ Γ Ξ )) 2 ( ( ) 2 ( 2 I I ML I I

ε

ξ

ovvero una differenza nell’autocentratura dipendente in modo sostanziale dalle caratteristiche fisiche e geometriche del sistema. 3. Modello Reale 3. Modello Reale 3. Modello Reale 3. Modello Reale

In questo capitolo presenteremo il modello matematico realizzato per GGG che ci permetterà di quantificare e comprendere i moti whirl che realmente incorrono nel sistema GGG [26]. Come prima cosa sarà necessario studiare i gradi di libertà di tale sistema e trovare delle coordinate generalizzate adatte a descriverlo. Essendo l’apparato sostanzialmente costituito da tre corpi (due masse e il braccio di accoppiamento) legati fra di loro da sospensioni cardaniche con bassa costante elastica sul piano orizzontale e alta costante elastica lungo la direzione verticale, possiamo dunque ragionevolmente supporre che il sistema possa essere descritto nella sue intierezza da sei coordinate generalizzate (2 gradi di libertà per ciascuno dei 3 corpi). Le sei coordinate generalizzate sono state scelte come due variabili angolo da associare ad ogni corpo (due masse e braccio di accoppiamento). Ed esse sono: ( k∈

{

a,1,2

}

a seconda che l’angolo sia riferito al braccio accoppiamento, al cilindro interno oppure al cilindro esterno)

ϑ’k : l’angolo variabile fra [0,π] rappresentante l’angolo rispetto alla verticale z

ϕ’k: l’angolo variabile fra [0,2π] rispetto all’asse ξ nel sistema di riferimento rotante in direzione antioraria.

Dunque il vettore Q=[q1,..,q6] t rappresenterà il vettore posizione nel nostro sistema di coordinate con:

q1=ϑ’a q4=ϕ’a q2=ϑ’1 q5=ϕ’a q3=ϑ’2 q6=ϕ’a

Mentre il vettore Q& rappresenterà le relative velocità.

A questo punto illustriamo il modello matematico relativo al sistema. La figura sottoriportata rappresenta la modellizzazione dell’apparato meccanico nel sistema di riferimento (O,ξ,η,z) rotante con

l’albero del rotore ad una frequenza angolare ω_s=2πν_s attorno all’asse z. La barra rappresentata in giallo è l’albero del rotore che è collegato al braccio di accoppiamento di massa ma e lunghezza 2L+∆L. La quantità ∆L rappresenta l’errore nella sospensione del braccio, cioè il punto di sospensione MP dista ∆L/2 dal centro reale del braccio di accoppiamento. Il vettore ε rappresenta la distanza del punto di sospensione del braccio dall’asse di rotazione, tenente di conto dei possibili errori nel montaggio o nella costruzione dell’apparato. La massa teste esterna m₂ è sospesa ad una distanza L2 da una estremità del

braccio di accoppiamento e similmente fig III.8: modello matematico di GGG quella interna m1 è sospesa ad una distanza L1 dall’altra estremità. I rettangoli rossi rappresentano le sospensioni cardaniche per le quali è supposta un’anisotropiaΛ come nei modelli precedenti.

Rispetto a questo sistema di riferimento i versori unitari indicanti le posizioni delle braccia sono: )] cos( ), sin( ) sin( ), cos( ) [sin( ˆ a a a a a a L =

ϑ

ϕ

ϑ

ϕ

−

ϑ

)] cos( ), sin( ) sin( ), cos( ) [sin( ˆ 1 1 1 1 1 1 = ϑ ϕ ϑ ϕ − ϑ L )] cos( ), sin( ) sin( ), cos( ) [sin( ˆ 2 2 2 2 2 2 = ϑ ϕ ϑ ϕ − ϑ L

E i vettori di posizione del centro di massa del braccio di accoppiamento, della massa interna e della massa esterna sono:

2 2 1 1 1 1 ˆ ˆ ) 2 ( ˆ ˆ ˆ 2 L L L L L r L L L L r L L r a a a a + ∆ + − = + + = ∆ − =

ε

ε

ε

r r r r r r

Per quanto riguarda invece i momenti di inerzia principali dei cilindri di GGG, chiamando R_i il raggio interno del cilindro, R_e il raggio esterno e R_h l’altezza del cilindro essi risultano essere

{

,1,2

}

) ( 2 1 ) 3 3 3 ( 12 1 2 , 2 , , , , 2 , 2 , 2 , , a R R m I I I R R R m I e i h e i ∈ ∀        + = = + + = Γ Ξ Η Ξ

λ

λ λ λ λ λ λ λ λ λ λ λ

Per calcolare la Lagrangiana del sistema possiamo rifarci alle formule sintetizzate per il modello del paragrafo precedente. Nel paragrafo precedente avevamo infatti trovato la formula della Lagrangiana relativa ad un corpo a simmetria cilindrica rotante in un sistema di riferimento rotante in funzione di coordinate generalizzate θ, ϕ che risultava essere:

) , , , ( ) , , , ( U ) , , , ( V ) , , , ( T ) , , ,

L(

θ

φ

θ

&

φ

& = _kin

θ

φ

θ

&

φ

& + _Cor

θ

φ

θ

&

φ

& + _Centr

θ

φ

θ

&

φ

& −U

θ

φ

θ

&

φ

& dove i singoli termini erano dati da

) sin ( 2 1 2 1 2 ₊

_φ

_&2 2

_θ

₊

_θ

_&2 = MV I_Ξ kin T

θ

ω

θ

φ

ω

ω

) sin cos ( _s R I _s 2 I _s2 V M ⋅ × + _Ξ + _Γ = & Cor V

θ

ω

ω

2 2 2 sin ) ( 2 1 ) ( 2 1 s s R I I M × + _Ξ− _Γ = Centr U

E il termine U doveva essere esplicitato. Assegnando dunque

λ

∈

{

a,1,2

}

rispettivamente al braccio di accoppiamento, al cilindro interno e al cilindro esterno, abbiamo che (1) { }

∑

∈ = 2 , 1 , a GGG λ λ L L

(2)

{

,1,2

}

, , a U I I I I M m V v R r ∈ ∀ = ⇒          →  →  →  →  →  Ξ Ξ Γ Γ

λ

φ

θ

φ

θ

_{λ λ λ λ λ} λ λ λ λ λ λ -) , , , ( T

L _tot & &

Dove abbiamo chiamato

(3) Ttot(

θ

,

φ

,

θ

&,

φ

&) =Tkin(

θ

,

φ

,

θ

&,

φ

&)+VCor(

θ

,

φ

,

θ

&,

φ

&)+UCentr(

θ

,

φ

,

θ

&,

φ

&) Per ottenere la Lagrangiana Lλ manca dunque di specificarne il potenziale Uλ . Esso

può essere facilmente ottenuto come somma di due componenti distinte: una dovuta al potenziale gravitazionale e l’altra dovuta al potenziale elastico.

(4) U_λ =Ug,_λ +Uelas,_λ

dove in perfetta analogia con il modello sviluppato nel paragrafo precedente abbiamo (5) U_g,λ =−mλg⋅Lλ ∀λ∈

{

a,1,2

}

e (6) ˆ ˆ ˆ ˆ

{ }

1,2 2 1 ˆ ˆ 2 1 2 2 2 2 , _ ∀ ∈     _{⋅ +Λ ⋅} + × = _{λ λ ξ} ξ η λ λ a a a a elas k l L L k L L L U

4.Le equazioni del moto linearizzate 4.Le equazioni del moto linearizzate 4.Le equazioni del moto linearizzate 4.Le equazioni del moto linearizzate

Una volta ottenuta la Lagrangiana del sistema è possibile ricavare le equazioni del moto in modo abbastanza semplice. Intanto notiamo che l’esperimento GGG è un’esperimento di zero, questo automaticamente porta a considerare il fatto che i moti che avvengono nella pratica operativa di GGG sono moti di piccolissima ampiezza vicini alla posizione di equilibrio del sistema. Questo autorizza certamente a considerare le equazioni del moto linearizzate, considerando delle piccole perturbazioni lineari delle coordinate attorno alla posizione di equilibrio ed espandendo la Lagrangiana fino al secondo ordine. A questo punto dalla equazioni del moto linearizzate potremo facilmente determinare le frequenze naturali del sistema che sono poi quelle che ci interessano per determinare le frequenze dei moti di whirl.

Il primo passo in questo processo consiste nel trovare le posizioni di equilibrio del sistema. Posizioni che sono determinate dal sistema di equazioni:

(1) 0 =0 ∀ =1,..,6 ∂ ∂ i q U i q i

Una volta rintracciati valori di equilibrio raccolti nel vettore Q0 _{consideriamo le} perturbazioni lineari attorno a tali posizioni di equilibrio definendo delle nuove variabili q’ 6 .. 1 ' ' 0 = ∀    = + = i q q q q q i i i i i & &

Di modo tale che in queste nuove coordinate

6 .. 1 0 0 0 0 = ∀     = = i q q i i &

A questo punto la nostra Lagrangiana linearizzata può essere scritta in termini

(2) = +

∑

+

∑

+

∑

+

∑

< < i j j i ij j j i i ij j i i j i ij i iq a q q b q q c q q b a ,

0 &' ' ' &' &' ' &' L

Dove i coefficienti a0, bi, aij, bij e cij sono funzioni della posizione di equilibrio e vengono calcolati numericamente. Per semplicità espositiva da adesso in avanti chiameremo le nostre coordinate q’i semplicemente qi sottointendendo il cambio di coordinate precedentemente fatto. A questo punto introduciamo le forze generalizzate Fi definite classicamente a partire dalle componenti in coordinate cartesiane delle forze agenti su ciascun corpo Fλ,j come

(3)

∑ ∑

= = ∂ ∂ ⋅ = a,1,2 3 1 , , λ λ λ j i j j q r F i F

Questa trattazione ci permette di prendere in considerazione ogni tipologia di forze che agiscono sul rotore per controllarne il comportamento dinamico. In particolare questa impostazione permette di tenere in considerazione le forze dissipative dovute all’attrito viscoso che –come abbiamo visto- sono la causa dell’incremento in ampiezza dei moti di whirl. In particolare nelle nostre integrazioni numeriche per simulare il comportamento di GGG sotto l’azione dei moti di whirl dovremo tenere in conto di un attrito rotante (che ha un carattere destabilizzante in rotazione supercritica) dato da (4)

∑

= −     _{− ⋅} Γ −     _{− ⋅} Γ − = 2 , 1 ˆ ) ˆ ˆ ( ˆ ˆ ) ˆ ˆ ( ˆ λ λ λ λ a a Rot a a a Rot rot a L L z z L L L L

e di un attrito non rotante (che invece ha un carattere stabilizzante sul rotore) dato da (5) Fa−nrot =−ΓNRot

[

vi +

ω

s×Li

]

Dove le matrici Γ sono le matrici con i coefficienti rappresentanti l’attrito viscoso che, come abbiamo visto dipendono sostanzialmente dal fattore qualità delle sospensioni laminari. Espandendo al primo ordine le equazioni delle Fi in cui sono state inserite le forze di attrito viscoso definiamo dei coefficienti α e β di modo che

(6) j j ij j j ijq

∑

q&

∑

+ = α β i F

A questo punto possiamo ricavare le equazioni del moto linearizzate definite dal metodo classico per cui

(7) = ∀ =1..6 ∂ ∂ ∂ ∂ i q q dt d i i i F L -L &

Dall’equazione linearizzata della Lagrangiana risulta

(8)

∑

∑

≠ + + = ∂ ∂ j j ji j i j ij i ii i q c q b q b q dt d & & & & & & 2 L e (9)

∑

∑

≠ + + = ∂ ∂ j j ij j i j ij i ii i q c q a q a q 2 & L

L’ i-esima equazione del moto linearizzata diventa così

(10) (1 ) ( (1 ) ) ( ) ( ( ) ) ( ) , , j j ij j j ji ij j i j j ij j ij ij j i j ij

ij b q&&

∑

a q

∑

q

∑

c c q&

∑

q&

∑

+δ = +δ + α + − + β

Che può essere scritta in modo molto più compatto in notazione matriciale

(11) _       ⋅ = ⋅ Q Q S Q M & & &

Dove M è una matrice reale 6x6 data da (12) Mij =(1+δij)bij

(13) S = A₂ +

[ ]

α

+C₂ +

[ ]

β

Che sono così definite:

(14)    ≤ < ≤ + = 12 6 0 6 ) 1 ( j j a A_ij

δ

ij ij (15)

[ ]

   ≤ < ≤ = 12 6 0 6 j j ij ij

α

α

(16)    ≤ < − ≤ = − − 6 12 6 0 ) 6 ( ) 6 ( c j c j C i j j i ij (17)

[ ]

   ≤ < ≤ = 12 6 6 0 j j ij ij

β

β

Le equazioni linearizzate del moto possono dunque scritte in modo semplice nella forma (18) _       ⋅ ⋅ = − Q Q S M Q & & & 1

Chiaramente M-1_{S è una matrice 6x12. Per motivi pratici conviene dunque definire} un nuovo vettore incognito di 12 componenti, che coinvolga anche le derivate prime delle coordinate generalizzate, ovvero introducendo il vettore x:

(19) t

Q Q x=( , &)

otteniamo una nuova forma per le equazioni del moto

(20) x Ax S M I x _ =      = 0|₋₁ &

Dove stavolta la matrice A è una matrice quadrata 12x12. Questo sistema differenziale è quello che ci interessa. Le sue soluzioni regolano completamente il comportamento dinamico di GGG in un’intorno della sua posizione di equilibrio, gli autovalori della matrice A forniscono invece il valore delle frequenze naturali del rotore ovvero ne indicano i modi normali. Quindi una volta fissata la matrice A, una semplice computazione numerica che ne determini gli autovalori permette di rintracciare i modi normali del sistema

5.I Modi Normali di GGG (simulazione e confronto con gli esperimenti) 5.I Modi Normali di GGG (simulazione e confronto con gli esperimenti) 5.I Modi Normali di GGG (simulazione e confronto con gli esperimenti) 5.I Modi Normali di GGG (simulazione e confronto con gli esperimenti)

I parametri fondamentali che governano il sistema GGG e dunque che determinano univocamente la matrice A sono le caratteristiche geometriche e fisiche dei tre corpi, delle tre sospensioni laminari, la costante elastica di queste sospensioni, il fattore qualità Q, il vettore ε, l’errore ∆L nel bilanciamento del braccio di accoppiamento ed infine la frequenza di rotazione dei due corpi ω_s che può essere fatta variare. Di questi parametri alcuni sono fissati dalla costruzione geometrica del sistema come le caratteristiche fisiche dei corpi e le costanti elastiche delle molle. Altri, come il fattore qualità sono misurati a partire dagli esperimenti. Altri ancora sono inessenziali se presi entro certi limiti, come il vettore ε che non ha effetti sensibili sull’integrazione se il modulo appartiene al range realistico compreso fra 1µm e 200µm [14]. Volendo rappresentare le frequenze naturali del sistema in relazione alla variazione della frequenza di rotazione ω_s, i parametri che devono essere inseriti per ricavare la matrice A(ω_s) sono rappresentati nella tabella seguente.

Per le masse

Per le sospensioni

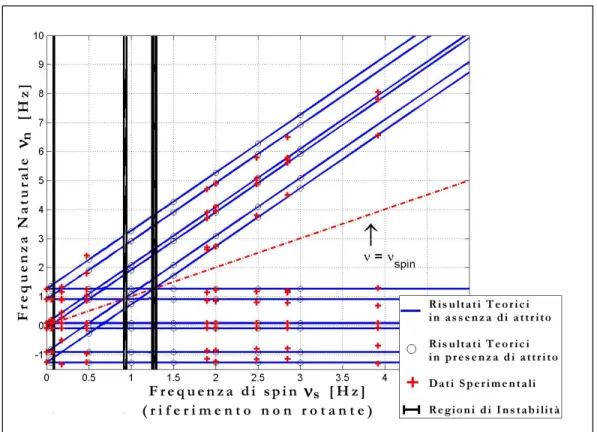
Una volta inseriti i parametri della matrice A, MatLab fornisce gli autovalori di tale matrice in funzione della frequenza di rotazione del sistema. Chiamando ν_s=ω_s/2π la frequenza di spin e ν_n le frequenze naturali risultanti, riportiamo in figura il risultato di questa integrazione numerica.

fig III.9: Modi Normali di GGG (risultati teorici e dati sperimentali)

Le linee blu del diagramma rappresentano i valori teorici calcolati in assenza di attrito viscoso, le croci rosse i valori sperimentali ottenuti, i cerchi bianchi bianchi rappresentano i dati teorici in presenza di attrito viscoso, le linee nere rappresentano le regioni di instabilità e la linea rossa tratteggiata separa la regione subcritica da quella supercritica. Cerchiamo di commentare questo diagramma per evidenziarne il significato.

In primo luogo notiamo che i cerchi bianchi sono tutti più o meno situati sulle linee blu, il che significa che l’attrito viscoso –come era lecito attendersi- non influenza significativamente i valori delle frequenze naturali del sistema. L’attrito viscoso – come l’abbiamo considerato nel capitolo sulla dinamica dei rotori- non agiva infatti modificando le frequenze naturali del sistema, ma agiva direttamente sull’ampiezza dei moti di whirl. L’attrito viscoso, infatti, non modifica l’andamento delle linee blu, ma agisce allargandole, cioè ingrandendo il range di sensibilità di queste frequenze naturali.

In secondo luogo notiamo che i risultati degli esperimenti coincidono molto bene con i dati teorici avvalorando il modello matematico sviluppato. Per ottenere tali risultati dagli esperimenti è stato necessario scomporre in armoniche (con la FFT) il segnale rilevato nell’esperimento e trasformato per il riferimento non rotante e considerare i picchi di ampiezza maggiore. E’ interessante notare che mentre i picchi relativi a frequenze supercritiche ( ν_n < ν_s ) sono sempre stati trovati e registrati, alcuni picchi invece nelle regioni subcritiche ( ν_n > ν_s ) non sono stati rilevati perchè di ampiezza troppo bassa. Tuttavia, a parte queste piccole discrepanze, il modello

matematico sembra essere in perfetto accordo con i dati sperimentali anche per frequenze di rotazione molto alte.

Continuando nell’analisi del grafico, notiamo che vi sono sostanzialmente due tipologie di frequenze naturali, le prime che rimangono costanti indipendentemente dalla velocità di rotazione del sistema, le seconde che crescono linearmente con la crescita della frequenza di rotazione (∆ν_n ≈ 2 ∆ν_s ). Questo fenomeno abbiamo visto essere un fenomeno tipico dettato dall’anisotropia della costante elastica. Questa anisotropia divide le singole frequenze di naturali in due componenti : una che rimane praticamente costante con l’aumentare della velocità di rotazione e l’altra che tende ad aumentare secondo la legge approssimata ∆ν_n ≈ 2 ∆ν_s . Le sei frequenze naturali del sistema si dividono dunque in dodici frequenze naturali di cui sei continuano costantemente a rimanere nella regione supercritica, mentre le altre sei tendono a spostarsi in regione subcritica (quindi ad alzare la loro frequenza).

fig III.9: i tre modi normali fondamentali di GGG

Studiando il modello teorico in un intorno di ν_s ≈ 0 possiamo notare le frequenze naturali del sistema non rotante che sono sostanzialmente tre (se non consideriamo il segno) come ci si aspetterebbe dallo studio di tre corpi accoppiati fra loro da tre molle ideali. Le tre frequenze risultanti hanno valore 0.09 Hz, 0.91 Hz e 1.26 Hz. Ovviamente accanto a questi valori positivi delle frequenze naturali che sono correlati ad i moti di whirl diretti , vi sono anche i valori negativi -0.09 Hz, -0.91 Hz

e -1.26 Hz, correlati ai moti di whirl inversi, quindi possiamo ambivalentemente dire che vi sono tre o sei frequenze naturali a seconda del fatto che le consideriamo in modulo o anche in verso di rotazione.

Aumentando sensibilmente la frequenza di rotazione del sistema abbiamo che le tre (sei) soluzioni si biforcano generando altre tre (sei) frequenze naturali. E’ naturale chiedersi come ciò possa accadere. Ingrandendo l’immagine iniziale ci rendiamo facilmente conto che quelle che sembrano singole frequenze naturali del caso non rotante, in realtà sono due frequenze naturali molto ravvicinate fra di loro.

fig III.10: Effetti dell’anisotropia della costante elastica sui modi normali di GGG

L’effetto in questione è dovuto all’anisotropia della costante elastica che raddoppia le frequenze naturali trasformando quella che era una singola frequenza naturale nel caso ideale in due distinte frequenze naturali (in questo caso distanti fra di loro di un termine dell’ordine dei 10-2 _{Hz) delle quali una è crescente con la frequenza di} rotazione e l’altra rimane costante.

Un altro effetto dettato dall’anisotropia della costante elastica è data dalla creazione di precise regioni di instabilità. Sappiamo dalla teoria (valida anche nel caso ideale) che in caso di coincidenza fra velocità di rotazione e frequenza naturale le vibrazioni meccaniche aumentano esponenzialmente di intensità. Tale crescita di intensità però cessa subito appena passati i valori relativi a queste frequenza naturali. Da un punto

di vista grafico possiamo dire che quando la linea tratteggiata in rosso interseca una linea blu, l’ampiezza del moto a quella frequenza cresce esponenzialmente.

Nel caso di anisotropia della costante elastica, però, la faccenda si complica: come possiamo notare dal diagramma, infatti, la linea tratteggiata in rosso non interseca più solo una linea blu, ma ne interseca sempre due contemporaneamente. Cerchiamo di capire meglio il fenomeno: in generale abbiamo che per ogni frequenza naturale positiva (indicante un moto di whirl diretto), ne esiste una negativa (indicante un moto di whirl inverso) e abbiamo detto che nel caso di anisotropia della costante elastica ciascuna di queste singole frequenze naturali si scindono in due componenti separate (δν≈ 10-2 Hz) di cui una dipende dalla frequenza di rotazione e l’altra rimane costante. Poichè la componente dipendente dalla velocità cresce di un fattore 2 rispetto alla velocità di rotazione, quando la velocità di rotazione arriva in prossimità di quella che era una singola frequenza di naturale del sistema, si ritrova vicino anche ad un’altra frequenza naturale corrispettiva a quel ramo della frequenza naturale negativa che è cresciuto con l’aumentare della velocità. Succede dunque che in prossimità di tali frequenze due moti di whirl di frequenza ravvicinata, ma distinta, crescano esponenzialmente in ampiezza generando una regione di totale instabilità del sistema in cui è impossibile lavorare.

fig III.10: regione di instabilità del sistema dettata dall’anisotropia della costante elastica

Come si vede dall’immagine ingrandita, poichè i moduli di tali frequenze erano sfasati di circaδν≈ 10-2 _{Hz, essi creano una regione di instabilità dell’ordine di δν≈ 10}-2 _Hz centrata su quella che era la frequenza naturale nel caso ideale. Da un punto di vista operativo, per passare queste regioni di instabilità dettate dall’anisotropia della costante elastica, è necessario attenuare le vibrazioni con un attenuatore passivo non ruotante.

II. Simulazione per i

II. Simulazione per i

II. Simulazione per i

II. Simulazione per il Controllo dei Moti di Whirl

l Controllo dei Moti di Whirl

l Controllo dei Moti di Whirl

l Controllo dei Moti di Whirl

1. Modello Matematico per il controllo dei moti di whirl 1. Modello Matematico per il controllo dei moti di whirl 1. Modello Matematico per il controllo dei moti di whirl 1. Modello Matematico per il controllo dei moti di whirl

Dalla Prima Parte (cap II.3) abbiamo dedotto che l’attrito viscoso non rotante ha sempre un effetto stabilizzante sui moti di whirl, a differenza dell’attrito viscoso rotante che invece può avere un effetto destabilizzante. Per cui per l’ammortizzazione dei moti di whirl in GGG si è deciso di procedere grazie all’ausilio di otto piastre capacitive (vedi Parte Prima I.3) a quattro delle quali viene applicato un voltaggio che simuli un attrito viscoso non rotante. Quattro piastre capacitive svolgono la funzione di sensori che rilevano spostamento e velocità del cilindro esterno, il segnale viene dunque elaborato al computer e viene ricostruito il segnale da applicare alle piastre per una simulazione di attrito viscoso non rotante.

Al fine di simulare il comportamento dinamico di GGG sotto l’effetto del controllo attivo dei moti di whirl è necessario estendere le equazioni linearizzate che regolavano l’evoluzione dinamica del sistema GGG al caso in cui sono presenti delle forze esterne. In questo caso è necessario modificare il sistema trovato in (I.4) aggiungendo un termine dettato dalle forze esterne, quindi all’equazione ( ) dobbiamo aggiungere (1) Fg Q Q S M Q _+       ⋅ ⋅ = − & & & 1

dove Fg rappresenta le forze generalizzate, ovvero se chiamiamo u la forza di controllo nelle coordinate del riferimento rotante abbiamo

(2)

( )

∑

= ∂ ∂ ⋅ = ζ η, , 2 j i j i g q r u F

dalla quale definiamo la matrice B di modo da modificare la ( ) nell’equazione

(3) x&= Ax+Bu

2. Implementazione della Simulazione 2. Implementazione della Simulazione 2. Implementazione della Simulazione 2. Implementazione della Simulazione

Il nucleo centrale del modello è stato realizzato nell’ambiente Simulink di MatLab 6. Lo schema generale del modello realizzato è quello rappresentato in figura.

fig III.12:Schema di Simulink per l’implementazione della simulazione sul controllo dei moti di whirl in GGG

Il programma per poter girare richiede in input le variabili matrice A, B, C e D che devono precedentemente essere memorizzate all’interno dell’ambiente MatLab. La Matrice C è semplicemente una trasformazione dalle coordinate generalizzate allo spostamento lungo le due coordinate η, ζ del sistema di riferimento rotante, la matrice D invece al momento (nella corrente simulazione) è formata esclusivamente da zeri, mentre le matrici A e B sono costruite in base alle formule () e () . Ad esse devono essere affiancate una serie di variabili ricavate dai parametri originali del sistema e dalla frequenza di rotazione del sistema. L’output del programma sono tre vettori t, x_nr e y_nr che forniscono i dati dello spostamento relativo fra i due cilindri lungo l’asse x e y nel riferimento non rotante al tempo t.

Il primo blocco trasforma il vettore y acquisito nel riferimento rotante nel vettore NR

y relativo al riferimento non rotante attraverso la semplice applicazione di una rotazione la cui matrice R è data da

(1)       − = ) cos( ) sin( ) sin( ) cos( t t t t R s s s s

ω

ω

ω

ω

Questa operazione è ottenuta in ambiente Simulink implementando il blocco qui rappresentato

fig III.14: Schema del passaggio dal sistema rotante al sistema non rotante

Questo blocco produce le componenti della posizione del cilindro esterno nel sistema di riferimento non rotante al tempo t che vengono memorizzate nel Workspace di Matlab separatamente e poi riunite in un unico vettore destinato all’elaborazione successiva.

Il blocco rappresentato qui in figura invece rappresenta il simulatore degli errori dovuti alla sensibilità degli strumenti dell’esperimento. Un errore costante nella rilevazione della posizione di circa 10 µm è sommato ad un errore casuale Il Blocco Simulink “Noise” si occupa di generare una serie di numeri causali secondo una distribuzione normale di media zero e varianza uno. Questo viene moltiplicato per un coefficiente che ne modella l’ordine di grandezza. Una stima realistica per questo coefficiente è circa 10-7_{. Nel blocco sono implementati due errori indipendenti fra di} loro che vanno ad influenzare il segnale lungo l’asse x e l’asse y.

fig III.15: Schema del generatore di rumore

Il rumore generato indipendentemente lungo i due assi va poi a formare un unico vettore che si somma al vettore posizione nel riferimento rotante ottenendo così una simulazione del vettore di posizione rilevato dall’apparato. Il vettore posizione viene poi diviso nuovamente in due componenti analizzate separatamente nei blocchi Channel 1 e Channel 2.

fig III.16:Blocco Channel 1per il filtraggio e la costruzione della forza di controllo

In questi blocchi la distanza viene convertita in voltaggio a mezzo del blocco Volt/m. Successivamente il segnale passa attraverso un filtro passa-banda che taglia le frequenze minori di 10-2_{Hz e superiori a 3Hz.}

Successivamente del segnale risultante vengono selezionate le componenti spettrali relative alle tre frequenze normali alle quali avvengono i moti di whirl stabili cioè 0.09 Hz, 0.91 Hz e 1.26 Hz grazie all’uso di tre filtri sentrati su quelle frequenze. Il blocco Zero-Holder simula un campionamento alla frequenza stabilita (in questo caso 10 Hz)

fig III.17: Filtro per isolare le frequenze interessanti per i moti di whirl

Dopo la simulazione di campionatura e il filtraggio alle frequenze desiderate, deve essere calcolata la velocità di whirl. E’ possibile calcolare la velocità di whirl in modo computazionalmente efficente direttamente a partire dal raggio di whirl.

Come descritto nella parte II infatti il raggio di whirl può essere scritto come

(2) r r (e (cos( wt),sin( wt)) t w w w

ω

ω

τ = dove Q w w 2 1

ω

τ

− =

derivando rispetto al tempo abbiamo

(3) r re 1 (cos( t),sin( t)) r e _w( sin( _wt),cos( _wt))

t w w w w t w w w w

ω

ω

ω

ω

ω

τ

τ τ − + = &

Se Q è molto alto, allora

τ

w <<

ω

w

−1

e quindi è possibile trascurare il primo termine ottenendo (4) ) 4 ( )) cos( ), sin( ( w w w w w w t w w T t r t t e r r_& ≈ τw

ω

−

ω

ω

=−

ω

−

che rende possibile trasformare il vettore posizione in un vettore velocità operando semplicemente una moltiplicazione per scalare ed un cambiamento di fase, blocco che operativamente viene implementato nella figura sottostante.

fig III.18: calcolo della velocità nel sistema di riferimento non rotante

A questo punto deve essere calcolata la forza di controllo da applicare. La forza di controllo viene applicata mediante quattro piastre capacitive (due lungo l’asse x e due lungo l’asse y) imponendo loro una variazione di potenziale proporzionale alla velocità di whirl. Per farlo calcoliamo la tensione da applicare alle piastre esterne ai cilindri. Prendendo come esempio le piastre lungo l’asse x poniamo la differenza di potenziale proporzionale alla velocità di whirl e positiva per una piastra e negativa per l’altra. Avendo come tensione base 180 Volts otteniamo così i due voltaggi per le due piastre (V± =V0±

α

vx). La Forza di controllo risultante sarà dunque

(5) ( ) 2 1 2 2 2 0 + − − = V V d S F_cx ε

Una situazione analoga varrà per l’asse y. Per ogni componente del vettore, dunque il blocco da implementare sarà quello sotto riportato che ripercorre i passggi da noi fatti con il semplice accorgimento di porre un blocco di saturazione che taglia le differenze di potenziale superiori a 360 V o inferiori a 0 V.

A questo punto il segnale viene riconvertito in un vettore di posizione nel riferimento rotante grazie all’implementazione del blocco “Form Non-Rotating to Rotating Reference” che altro non è che la moltiplicazione per la matrice inversa del blocco iniziale per il cambio di riferimento

fig III.20: Schema per il passaggio dal sistema di riferimento non rotante a quello rotante Successivamente questa uscita viene reintrodotta nel sistema per una nuova elaborazione del processo.

3. Risultati della Simulazione e confronto con gli esperimenti 3. Risultati della Simulazione e confronto con gli esperimenti 3. Risultati della Simulazione e confronto con gli esperimenti 3. Risultati della Simulazione e confronto con gli esperimenti

Tutto il programma produce in uscita due vettori relativi all’asse x e all’asse y che poi vengono visualizzati ed elaborati con MatLab. Questo è un esempio del risultato dell’elaborazione riguardo al controllo di whirl risultante. La linea rossa indica l’asse Y alla quale non è stato applicato il controllo, mentre la linea blu indica l’asse a cui è stato applicato il controllo. Il tutto è visualizzato nel riferimento rotante

La figura seguente invece rappresenta lo stesso risultato applicato nel riferimento rotante, stavolta il controllo è applicato lungo l’asse Y.

fig III.22: Simulazione di un controllo dei moti di whirl lungo l’asse y (riferimento non rotante) Infine la figura seguente rappresenta una visualizzazione del controllo lungo l’asse X e Y simultaneamente (partendo da due condizioni iniziali leggermente diverse per facilitare la visualizzazione del controllo).

fig III.23: Simulazione di un controllo dei moti di whirl lungo entrambi gli assi (riferimento non rotante)