3. Metodi di calcolo 3.1 Le strutture di sostegno

3. Metodi di calcolo

3.1 Le strutture di sostegno

Le opere di sostegno sono delle strutture in grado di contrastare le spinte esercitate da un fronte di terreno instabile. In generale esse vengono distinte in due categorie: opere di sostegno rigide, caratterizzate dal fatto che l’unico movimento che possono manifestare sotto l’azione dei carichi in gioco è un movimento rigido, e quelle flessibili, caratterizzate invece da una certa deformabilità. La stabilità è legata nel primo caso al peso dell’opera stessa e/o a quella del terreno che grava sulla suola di fondazione; nel secondo caso invece l’equilibrio è assicurato dalla mobilitazione della spinta passiva nella parte infissa ed eventualmente dalla presenza di altri vincoli, quali ad esempio un sistema di ancoraggio. In entrambi i casi l’entità e la distribuzione delle azioni che il terreno esercita sull’opera sono legate all’entità ed al tipo di movimento che essa manifesta. Pertanto la determinazione di tali azioni richiede a rigore la risoluzione di un problema di interazione terreno-struttura. Tuttavia si ricorre sovente a soluzioni approssimate come i metodi dell’equilibrio limite, supponendo che il terreno si trovi in condizioni di scorrimento plastico e assumendo così nota a priori la distribuzione delle azioni all’interfaccia.

Nelle costruzioni marittime sono spesso utilizzate opere flessibili come le palancolate. Questo perché possono essere adoperate in condizioni di terreno molto sfavorevoli, come quello di riporto o di colmata presente in tanti porti, non richiedono fondazioni e le caratteristiche scadenti favoriscono, inoltre, l’infissione dal piano di campagna. Laddove altre opere di sostegno possono risultare di difficile realizzazione, le palancolate presentano il vantaggio di poter essere infisse anche in acqua da pontili o chiatte. Esse sono realizzate in legno, cemento armato oppure in acciaio. Quest’ultimo è il materiale più adottato nelle costruzioni marittime perché presenta numerosi vantaggi: la varietà delle sezioni trasversali e la conseguente ampia gamma di resistenze a flessione, l’economia, l’assenza di svergolamento durante l’infissione, la possibilità di combinare i diversi profili per aumentare la rigidezza della sezione trasversale, la possibilità di recuperare e riutilizzare i profilati per lavori provvisionali, la leggerezza,

3.2 Metodi di calcolo delle opere di sostegno

3.2.1 Spinta delle terre

Lo spostamento di un’opera di sostegno può avvenire in diversi modi ognuno dei quali ha un effetto importante sulle spinte del terreno. Il quadro può essere chiarito introducendo il coefficiente di spinta K:

v h K ' ' σ σ =

dove σ’h e σ’v rappresentano rispettivamente la tensione orizzontale efficace e la

tensione verticale efficace alla generica profondità al di sotto del piano di campagna; si può osservare che quando la parete non subisce spostamenti, il terreno esercita una pressione su di essa ed il coefficiente di spinta non è nullo. Se si permette alla parete di spostarsi per effetto della pressione del terreno e perciò di allontanarsi da esso, tale pressione e, di conseguenza, il coefficiente di spinta si riducono. Il valore minimo del coefficiente di spinta si raggiunge per spostamenti orizzontali relativamente piccoli, circa 0,1-0,2% dell’altezza dell’opera. Ulteriori incrementi di spostamento non producono ulteriori riduzioni di spinta. Se la parete invece viene spostata dalla sua posizione originale, avvicinandola al terreno, il coefficiente di spinta aumenta e continua ad aumentare anche per spostamenti molto maggiori (2-8% per sabbie dense e 5-20% per sabbie sciolte) di quelli che corrispondono alla piena mobilitazione del coefficiente di spinta minimo. Anche in questo caso, tuttavia, per spostamenti laterali elevati si raggiunge un valore costante del coefficiente di spinta. Il valore minimo, quando la parete si allontana dal terreno, è denominato coefficiente di spinta attiva (KA),

mentre quello massimo, quando la parete è spinta verso il terreno, è denominato coefficiente di spinta passiva (KP). Se gli spostamenti orizzontali della parete sono

impediti, il rapporto tra la tensione efficace orizzontale e quella verticale è detto coefficiente di spinta a riposo (K0).

La ragione per cui tale coefficiente varia in funzione dello spostamento della parete è il progressivo sviluppo di tensioni di taglio nel terreno via via che la parete si sposta dalla sua posizione iniziale “a riposo”. Quando gli spostamenti sono sufficienti per mobilitare la resistenza a taglio del terreno, l’entità delle sollecitazioni applicate alla

struttura di sostegno dipende dai parametri di resistenza del terreno. Il valore del coefficiente di spinta, quindi, dipende da:

• Spostamenti dell’opera

• Attrito mobilitato al contatto tra terreno e opera • Parametri di resistenza del terreno

• Geometria dell’opera di sostegno e del terrapieno

La teoria di Coulomb (1776), o metodo dell’equilibrio limite, considera l’equilibrio globale di un cuneo di terreno delimitato dalla parete, dalla superficie limite del terreno e dalla potenziale superficie di scorrimento definita

piana (Figura 3.1). Assumendo che la spinta attiva agisca secondo una direzione prefissata, essendo nota anche la direzione delle reazioni del terreno, è possibile determinare il suo valore dall’equilibrio del cuneo. La superficie di scorrimento è una superficie di tentativo; il procedimento va ripetuto per varie superfici fino ad ottenere il valore massimo della spinta attiva. Tale metodo prescinde dall’analisi delle condizioni di

equilibrio locale. Non è nota la distribuzione delle tensioni sul paramento del muro e il punto di applicazione della spinta deve essere determinato in modo indipendente. Se il cuneo di spinta ha forma triangolare, il punto di applicazione della spinta attiva è a una distanza dalla base pari a H/3.

La soluzione formulata successivamente da Rankine (1857) considera simultaneamente, per un prisma elementare di terreno, le equazioni di equilibrio e le condizioni di rottura. Ipotizza, inoltre, l’assenza di attrito tra muro e terreno e, nel caso particolare di terrapieno orizzontale e paramento interno del muro verticale, è esprimibile tramite le equazioni:

A v v A ⎟= ⋅K ⎠ ⎞ ⎜ ⎝ ⎛ _°− ⋅ = 0 2 0 ' 2 ' 45 tan ' ' σ φ σ σ P v v P ⎟= ⋅K ⎠ ⎞ ⎜ ⎝ ⎛ _°+ ⋅ = 2 ₀ 0 ' 2 ' 45 tan ' ' σ φ σ σ

Figura 3.1: teoria di Coulomb

(3.3) (3.2)

Nelle quali σ’v0 è la tensione verticale efficace, σ’A e σ’P sono rispettivamente la

pressione limite attiva e passiva, KA e KP i coefficienti di spinta attiva e passiva. Qualora

le condizioni al contorno ipotizzate dalla teoria di Rankine siano soddisfatte, la soluzione di Coulomb e quest’ultima vengono a coincidere. Poiché al contatto muro-terreno sono sempre presenti forze di

attrito, tali condizioni non si riscontrano mai in pratica e i calcoli basati sulle equazioni di Rankine comportano determinati errori.

Il procedimento dell’equilibrio limite di Coulomb è stato esteso successivamente per via analitica da Müller-Breslau ai casi più generali illustrati in Figura 3.2.

Le equazioni che danno i valori di KA e KP risultano le seguenti:

(

)

(

)

₍

(

₎

)

( )

₍

₎

2 2 2 cos cos ' sin ' sin 1 cos cos ' cos ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⋅ + − ⋅ + + ⋅ + ⋅ − = i i KA β δ β φ φ δ δ β β β φ

(

)

(

)

₍

(

₎

)

₍

( )

₎

2 2 2 cos cos ' sin ' sin 1 cos cos ' cos ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⋅ − + ⋅ + − ⋅ − ⋅ + = i i K_P β δ β φ φ δ δ β β β φ

con φ’ angolo di attrito efficace, β inclinazione del paramento interno, δ angolo di attrito muro-terreno, i inclinazione del terrapieno di monte.

L’assunzione di una superficie di scorrimento piana non è però congruente con l’ipotesi che vi sia attrito muro-terreno, per cui, mentre il valore del coefficiente di spinta attivo calcolato con la teoria di Coulomb è in accordo con i valori deducibili da analisi più raffinate, quello del coefficiente di resistenza passiva risulta sovrastimato e pertanto non cautelativo. Alla luce di tali considerazioni risulta perciò lecito fare riferimento per il calcolo della spinta attiva (PA) a metodi quali quello di Coulomb con

superficie di rottura piana, mentre per il calcolo della spinta passiva (PP) sono da evitare

Figura 3.2: estensione della teoria di Coulomb

(3.5) (3.4)

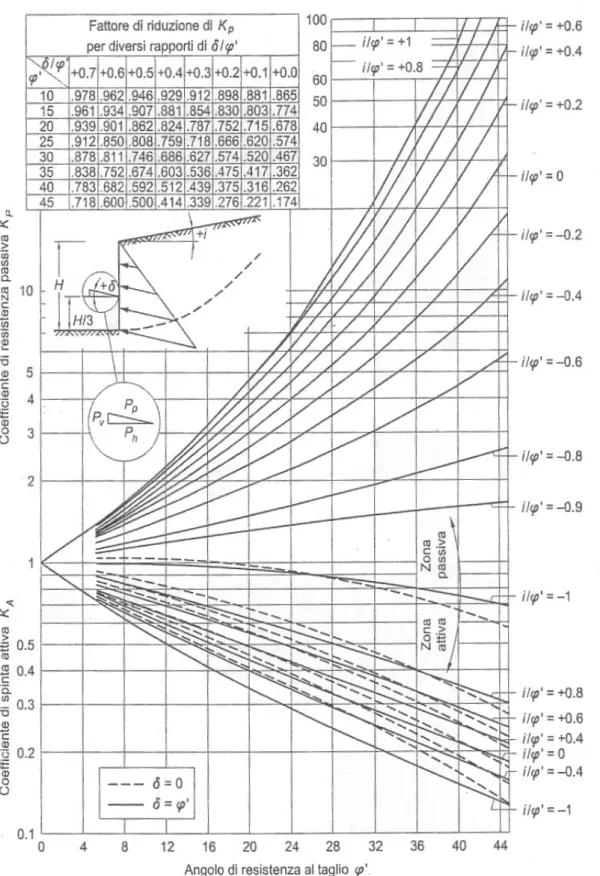
tutte le espressioni analoghe a quella di Coulomb ed occorre riferirsi solo a procedimenti che ipotizzino l’uso di superfici di scivolamento curvilinee, quali quelle ricavate da Caquot e Kerisel (1948) o i diagrammi di spinta riportati nel manuale NAVFAC (Figura 3.3).

La spinta attiva e quella passiva si calcolano dunque mediante le seguenti espressioni: A A H K P = ⋅ ⋅ 2 ⋅ 2 1 _γ

con KA calcolato con il metodo di Coulomb

P

P h K

P = ⋅ ⋅ 2 ⋅ 2

1 _γ

con KP calcolato, per esempio, interpolando i dati nel seguente grafico NAVFAC.

(3.7) (3.6)

3.2.2 Criteri di dimensionamento e verifica delle paratie

3.2.2.1 Paratie a sbalzo

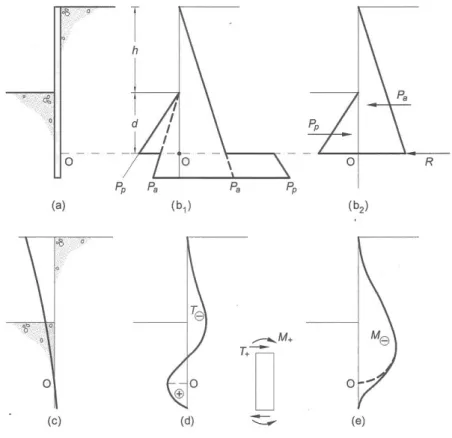
Il meccanismo di rottura (Figura 3.4) è rappresentato da una rotazione intorno al punto O, prossimo alla base, e la stabilità dell’opera è assicurata dalla mobilitazione della resistenza passiva, sia a valle della paratia nel tratto al di sopra del punto O, sia a monte nel tratto al di sotto di tale punto. L’analisi semplificata, che solitamente si effettua, ipotizza che la risultante della spinta attiva e della resistenza passiva agenti al di sotto del punto di rotazione, sia rappresentata dalla forza R applicata in O, considerando trascurabile il momento di trasporto. La lunghezza di infissione d si ottiene imponendo l’equilibrio alla rotazione intorno al punto O. La condizione di equilibrio alla traslazione orizzontale consente successivamente di valutare la reazione R e di definire quindi la lunghezza dell’ulteriore tratto al di sotto del punto O (in prima approssimazione si assume tale tratto pari al 20% della lunghezza di infissione d).

3.2.2.2 Paratie vincolate in testa (con ancoraggio o puntone)

La stabilità dell’opera è garantita dall’azione del vincolo suddetto e dalla mobilitazione della resistenza passiva. L’analisi limite può essere svolta con riferimento a due possibili alternative, a seconda dell’ipotesi che si introduce sulle condizioni di vincolo della parte palancolata immorsata nel terreno.

Metodo dell’estremo libero

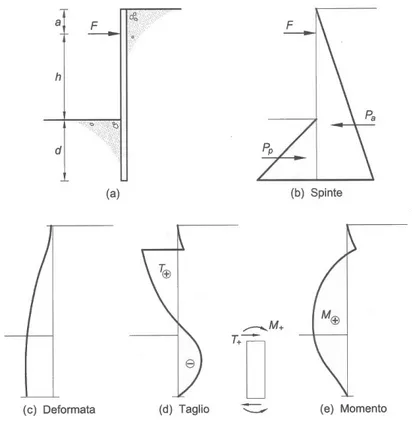
Il metodo ipotizza la parte inferiore della paratie semplicemente appoggiata per cui la struttura risulta, come per quelle a sbalzo, isostatica. Le condizioni di equilibrio sono sufficienti a ricavare le due incognite del problema, rappresentate dalla lunghezza di infissione d e dalla reazione del vincolo F (Figura 3.5). Ammettendo che la parete sia rigida, l’equilibrio alla rotazione intorno al punto di applicazione della forza F consente di determinare d: l’equazione può essere risolta assumendo un valore di tentativo della lunghezza di infissione e andando a verificare l’annullamento del momento nel punto di applicazione di F oppure esprimendo i valori delle spinte in funzione della lunghezza di infissione incognita; in quest’ultimo caso la condizione di equilibrio alla rotazione dà luogo ad un’equazione cubica in d.

Metodo dell’estremo fisso

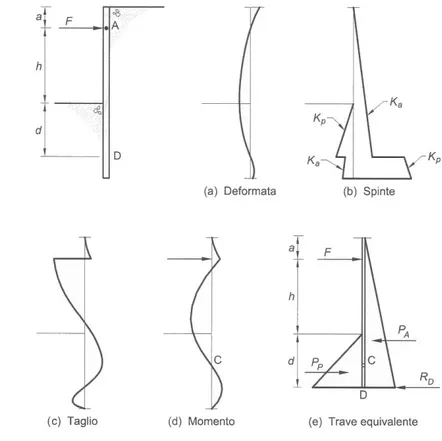
Il metodo assume che la paratia sia flessibile ma infissa (Figura 3.6) fino ad una profondità sufficiente per considerare l’estremità inferiore incastrata e può essere applicato a tutte le paratie, siano esse ancorate, rigide o flessibili, o a sbalzo. Le azioni agenti sulla struttura al di sopra del piede sono costituite da una forza concentrata, agente ad una certa distanza dall’estremità inferiore dove si ammette che la deformata abbia tangente verticale. La profondità di infissione si ottiene per tentativi finché lo spostamento a livello dell’ancoraggio rispetto al piede della struttura è nullo. Il calcolo può risultare complicato e per questo motivo esistono delle semplificazioni come il “metodo della trave equivalente” o metodo di Blum. In questo metodo si ammette che sia nota la posizione del punto D in corrispondenza del quale la tangente alla deformata della paratia è verticale. Questa ipotesi semplificativa rende possibile sostituire la distribuzione delle tensioni orizzontali all’estremità inferiore della palancolata con una forza concentrata (RD) e, partendo dall’assunto che in una struttura iperstatica non si può

prescindere dalle condizioni di congruenza, permette di calcolare la lunghezza di infissione. Osservando infatti che in corrispondenza del punto C (flesso) si ha momento

nullo, si può pensare di inserire in tale sezione una cerniera spezzando così la struttura in due travi separate: la prima semplicemente appoggiata e quella inferiore costituita da una mensola. La profondità a cui va posta la cerniera può assumersi, senza apprezzabili errori, pari mediamente al 10% dell’altezza a partire dal fondo scavo. L’equilibrio alla rotazione rispetto al punto A consente di determinare la reazione RC e, successivamente,

l’equilibrio alla traslazione permette di determinare la reazione F. Infine l’equilibrio alla rotazione intorno al punto D consente di determinare la lunghezza del tratto infisso. Il problema principale di questo metodo consiste nella corretta determinazione del punto di flesso nel caso di terreni stratificati. Per terreni uniformi, il punto C coincide approssimativamente con il punto in cui la spinta totale netta si annulla. Il metodo dell’estremo fisso determina profondità di infissione maggiori e momenti flettenti minori di quelli che si ottengono con il metodo dell’estremo libero.

3.3 Metodi di calcolo delle opere di sostegno in zona sismica

I metodi di calcolo proposti in letteratura possono essere classificati come segue: a. Metodi pseudo-statici

b. Metodi degli spostamenti c. Metodo delle tensioni

I metodi pseudo-statici e degli spostamenti fanno entrambi riferimento ad un comportamento rigido-plastico del terreno, mentre il metodo delle tensioni utilizza in generale una schematizzazione del suddetto come mezzo semplicemente elastico o elastico-perfettamente plastico. Nei metodi di tipo “a” la risoluzione del problema dinamico è effettuata con il criterio pseudo-statico mentre nei metodi “b” e “c” è effettuata prendendo in considerazione accelerogrammi artificiali, registrati o simulati (la cosiddetta “time history” del sisma).

3.3.1 Metodi pseudo-statici: Mononobe - Okabe

Il metodo può essere considerato come un’estensione in campo dinamico del criterio di Coulomb per la determinazione delle spinte attive sui muri di sostegno. Le assunzioni alla base del metodo sono riassunte come segue:

1. per effetto del sisma il muro trasla in direzione orizzontale di uno spostamento sufficiente a produrre all’interno del terreno una condizione di equilibrio plastico.

2. Il terreno è privo di coesione e soddisfa il criterio di rottura di Mohr-Coulomb. 3. Non c’è presenza di falda.

4. La superficie di rottura del terreno è piana, inclinata di α sull’orizzontale e passante per la base del muro.

5. Il muro è lungo abbastanza da poter trascurare gli effetti delle condizioni alle estremità.

6. Il cuneo di terreno compreso tra la superficie di scivolamento e la parete del muro (“cuneo di rottura”) si comporta come un blocco rigido di peso W, dotato di accelerazione a uguale in tutti i punti. Nel caso più generale l’accelerazione comprende sia la componente orizzontale ah che quella verticale av definite dalle

seguenti espressioni: g k

a_h = _h ⋅ ; a_v =k_v⋅g

dove kh è il coefficiente di intensità sismica in direzione orizzontale, kv è il

coefficiente di intensità sismica in direzione verticale e g l’accelerazione di gravità.

7. L’effetto del terremoto è tenuto in conto sostituendo l’inerzia del cuneo con la forza statica equivalente (“pseudo-statica”) di componenti k_h⋅ nella direzione W orizzontale e kv⋅W in quella verticale.

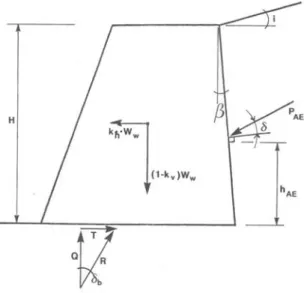
8. Il cuneo è considerato in equilibrio nella condizione di incipiente scivolamento sotto l’azione del peso W e delle forze pseudo-statiche indicate al punto 7 (Figura 3.7).

9. è ammessa l’esistenza di attrito al contatto muro-terreno.

La spinta attiva sul muro è ottenuta ricercando il valore massimo, rispetto all’inclinazione α della superficie di scivolamento, della spinta laterale PAE ricavata

dall’equilibrio del cuneo. Nella condizione critica, tale spinta agente sul muro risulta espressa dalla relazione seguente:

(

v

)

AE

AE H k K

P = ⋅ ⋅ 1− ⋅ 2

1 γ 2

in cui γ è il peso unitario del volume di terreno (per terreni sotto falda si dovrà assumere il peso unitario di volume efficace γ’ ), H è l’altezza del muro, KAE è il coefficiente di

spinta attiva del terreno in condizioni dinamiche che tiene conto sia del contributo statico che di quello dinamico.

L’equilibrio del cuneo fornisce per KAE l’espressione:

(

)

(

)

(

₍

)

₎

(

₍

)

₎

2 2 2 cos ' cos ' sin ' sin 1 cos cos cos ' cos ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⋅ + + − − ⋅ + + ⋅ + + ⋅ ⋅ − − = β θ φ δ θ φ φ δ θ β δ β θ β θ φ i i K_AE nella quale: − _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = v h k k 1 arctan θ

− φ’ è l’angolo di resistenza al taglio drenata del terreno − δ è l’angolo di attrito muro-terreno

− β è l’inclinazione rispetto alla verticale dell’intradosso del muro

− i è l’inclinazione rispetto all’orizzontale del piano di campagna del terrapieno. (3.9)

Nota PAE, la componente orizzontale della spinta può essere calcolata tramite

l’espressione:

(

PAE

)

_h =P_AE ⋅cos

(

δ +β

)

L’inclinazione α del piano di rottura associata alla (3.11), può essere ricavata dalla relazione di Wong (1982)

(

) (

)

(

)

⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⋅ + − ⋅ + ⋅ + ⋅ + − = Q P R P R Q Q P P 1 1 arctan ' θ φ α dove:

(

i

)

P=tanφ'−θ −

(

φ−θ −β

)

= ' tan 1 Q

(

θ +β +δ

)

= tan R

Seed e Whitman (1970) hanno investigato l’influenza dei vari parametri sul valore del coefficiente di spinta attiva, giungendo alla conclusione che la spinta PAE risulta

sensibilmente influenzata dal valore del coefficiente sismico in direzione orizzontale kh,

mentre è scarsamente rilevante l’effetto delle accelerazioni verticali kv, soprattutto per i

sismi di maggiore intensità e per i reali valori di kv. Tra gli altri parametri quelli che

risultano maggiormente influenti sono l’angolo di resistenza al taglio del terreno φ’ e l’inclinazione del terrapieno i ; quasi del tutto trascurabile è invece l’effetto dell’attrito muro-terreno δ. L’assunzione di δ uguale alla metà di φ’ può essere soddisfacente nella maggior parte dei casi.

Nonostante le inevitabili limitazioni insite nel metodo, dovute al fatto che si sostituisce una sollecitazione variabile nel tempo con un sistema di forze statiche, i risultati da esso forniti confermano le evidenze sperimentali e sono sicuramente a favore di sicurezza. Analogamente al metodo di Coulomb, il criterio di Mononobe-Okabe fornisce il valore della risultante delle pressioni laterali PAE senza dare indicazioni sulla

posizione del punto di applicazione. La distribuzione teorica delle pressioni laterali sia statiche che dinamiche dietro un muro dotato di attrito è non lineare e dipende da molti fattori quali:

• Esistenza o meno di un movimento rigido dell’opera;

(3.11)

• Tipo di movimento subito (traslazione, rotazione rispetto alla base, rotazione rispetto alla testa, etc.);

• Entità del movimento; • Flessibilità dell’opera;

• Caratteristiche del terrapieno (geometria, deformabilità, etc.); • Distribuzione delle accelerazioni all’interno del terrapieno

Nella pratica progettuale si preferisce, perciò, procedere adottando per la risultante totale PAE un punto di applicazione ubicato ad un’altezza della base compresa tra 0,4H e

0,5H (Bakeer, 1985): questo viene ottenuto considerando il contributo separato della componente statica PA e di quella dinamica ΔPAE, applicando la prima a 1/3 H dalla

base del muro e la seconda ad un’altezza compresa tra 1/2 H e 2/3 H. Seed e Whitman (1970) consigliano per il punto di applicazione di ΔPAE un’altezza pari a 0,6 H.

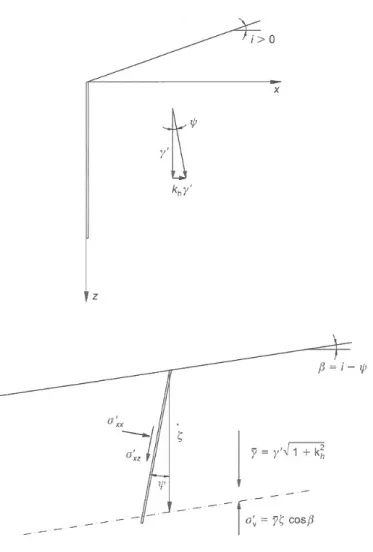
Per quanto riguarda la spinta passiva, così come nel caso statico, è riconosciuto ormai l’errore che si commette adottando metodi che ipotizzino una superficie di scorrimento piana, suggerendo quindi metodi dell’equilibrio limite che forniscano una superficie di scorrimento curvilinea (di solito una spirale logaritmica). Tuttavia queste procedure non sono a favore di sicurezza (essendo essenzialmente di natura cinematica) e se fossero assunte come meccanismo ammissibile in termini cinematici, rappresenterebbero il limite superiore della soluzione esatta. Lancellotta (2007) propone un metodo che permette la stima della resistenza passiva in condizioni sismiche utilizzando le stesse equazioni del caso statico ma con gli assi trasformati (Figura 3.8), ottenendo così il limite inferiore della soluzione esatta. L’espressione del coefficiente di spinta passiva in condizioni sismiche è la seguente:

(

)

2 2

(

)

(

cos sin2 ' sin2

)

2 tan '

sin ' sin cos cos _{δ φ δ ψ φ} θ φ θ δ _⋅ ⋅ ⋅ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + ⋅ − − − − = e i i K_PE

dove, oltre ai simboli già elencati in precedenza, si ha il coefficiente 2⋅ψ dato da

(

)

_δ

₍

_ϑ

₎

_ϑ φ θ φ δ ψ _⎟⎟+ + − + ⋅ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⋅ 2 ' sin sin arcsin ' sin sin arcsin 2 i i (3.13) (3.14)

Figura 3.8: Lancellotta (2007), trasformazione degli assi

Sull’ubicazione del punto di applicazione della spinta passiva, diversi regolamenti sismici di vari Paesi propongono, in analogia alla procedura adottata per la spinta attiva, di mantenere separato il contributo statico PP da quello dinamico ΔPAE. Risulta però

difficile se non impossibile separare le due componenti dato che, essendo il caso sismico peggiorativo, la spinta passiva in condizioni sismiche è minore di quella in condizioni statiche. Una soluzione possibile può essere quella di applicare la spinta passiva in condizioni sismiche PPE, che tiene conto sia del contributo statico che di

quello dinamico, ad una quota pari a 0,4⋅d, con d altezza di muro su cui insiste la spinta passiva.

3.3.2 Metodi degli spostamenti: Newmark

Il metodo si basa sul modello adoperato da Newmark (1965) per la descrizione del movimento di un blocco rigido su un piano ruvido di sostegno assoggettato ad accelerazioni sismiche (Figura 3.9).

Fino a quando le accelerazioni del terreno di appoggio sono piccole, il blocco

si muove solidalmente al piano e la forza d’inerzia agente su di esso può essere calcolata con riferimento all’accelerazione a del piano. In corrispondenza ad un valore limite

g N alim = ⋅

la tensione tangenziale sul piano di scorrimento uguaglia la resistenza di attrito limite al contatto blocco-terreno e si ha un inizio di scivolamento. Durante quest’ultimo l’accelerazione del blocco resta costantemente fissata sul valore limite raggiunto.

Nel caso semplice mostrato nella figura precedente in cui sono trascurate le forze d’inerzia verticali, la considerazione dell’equilibrio del blocco in direzione orizzontale fornisce N =tanδb, con δb angolo di attrito limite blocco-terreno. I valori di N sono limitati dalla condizione δ_b ≤φ'; in corrispondenza di δ_b =φ' si ha il massimo valore dell’accelerazione limite (accelerazione critica) definita da

g N a_crit = _crit⋅

con N_crit =tanφ'. Il metodo può essere facilmente esteso anche al caso in cui sia presente la componente verticale: in tal caso l’accelerazione limite prende il nome di accelerazione di soglia N’ (Whitman, 1979) e vale:

(

k

)

(

k

)

N

N'= 1− _v ⋅tanδ_b = 1− _v ⋅ ed il corrispondente valore critico diventa:

(

1

)

tan ' 'crit= −kv ⋅ φ N (3.15) (3.16) (3.18) (3.17) Figura 3.9: modello di Newmark

La solidarietà tra il blocco ed il terreno potrà essere ripristinata solo dopo che l’accelerazione del piano avrà subito una riduzione divenendo inferiore ad alim. Se si

fa l’ipotesi che il blocco possa spostarsi solo in un verso, nella schematizzazione di Figura 3.10 nella quale è presente un treno d’onde costituito da un solo impulso rettangolare, la velocità assoluta istantanea del blocco nell’intervallo di tempo 0 ÷ t2 ,

corrispondente alla durata della fase di scivolamento, sarà espressa da:

t g N vb = ⋅ ⋅

mentre quella del piano varrà:

t g k

v_g = _h⋅ ⋅ per 0≤t≤t₁

vg =vm per t1 ≤t ≤t2

dove vm =kh ⋅g⋅t1. L’istante t2 è definito dalla condizione vg =vm da cui si ottiene:

1

2 t

N k

t = h ⋅

La (3.22) esprime la circostanza che la durata t2 della fase di scivolamento è una

frazione kh/N >1 della durata critica t1 dell’impulso rettangolare di ampiezza a. Lo

spostamento relativo complessivo D subito dal blocco nell’intervallo di tempo 0 ÷ t2 è

rappresentato dall’area tratteggiata di figura. Per il caso considerato di un solo impulso rettangolare di ampiezza a>a_lim si ha:

g v k N D m h ⋅ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 2 1 2 1

essendo vm la velocità massima delle onde sismiche nel terreno. In presenza di un

“treno” d’onda costituito da Ni impulsi rettangolari di ampiezza a>alim, lo spostamento

complessivo sarà dato da:

(3.19)

(3.21) (3.20)

(3.22)

(3.23) Figura 3.10:accelerazioni e velocità

i m h N g v k N D ⋅ ⋅ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 2 1 2

Per “time history” più complicate, quali quelle dei sismi reali, le velocità e gli spostamenti sono ottenuti per successive integrazioni numeriche che richiedono il ricorso ad appositi programmi di calcolo. Come risultato si avranno fasi di movimento relativo alternato a fasi nelle quali il blocco ed il piano si muovono solidalmente tra loro. Analizzando i risultati delle integrazioni effettuate con gli accelerogrammi di 4 terremoti reali, Newmark concluse che questi potevano essere descritti in termini di “impulsi rettangolari” introducendo nella (3.24) un numero di impulsi “equivalente”:

( )

N k N h eq i = che andava a modificare la (3.24) come segue:

N k g v k N D m h h ⋅ ⋅ ⋅ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = 2 1 2

Avendo preso in esame le sole accelerazioni orizzontali, a rigore la (3.26) era da considerare valida per sismi nei quali il contributo dell’accelerazione verticale fosse trascurabile ma Franklin e Chang (1977) estesero l’analisi a 27 terremoti reali e 10 sintetici non riscontrando significative differenze.

Richards ed Elms (1979), facendo riferimento ad una curva interpolatrice più cautelativa e coincidente con l’inviluppo superiore di tutti i dati analizzati, adottarono la seguente espressione: 4 2 22 , 0 − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⋅ ⋅ ⋅ = h h k N g k V D

con V velocità di picco delle onde sismiche in [m/sec].

Essi proposero inoltre di estendere il modello di Newmark anche al caso dei muri di sostegno, assimilando questi ultimi a “blocchi” soggetti alle azioni di Figura 3.11. L’ipotesi alla base del metodo è che, in corrispondenza a ciascuna fase di “instabilizzazione” del

(3.24)

(3.25)

(3.26)

(3.27)

muro, si sviluppi, a tergo di questo, un cuneo di terreno plasticizzato delimitato da una superficie di rottura piana la cui spinta PAE può essere calcolata tramite la teoria di

Mononobe-Okabe. Inoltre è stata fatta l’assunzione semplificativa che, nelle fasi di movimento relativo, l’accelerazione del cuneo sia uguale a quella di soglia del muro e resti costante per tutta la durata del movimento. L’accelerazione di soglia N’ può essere valutata analizzando l’equilibrio del muro nelle condizioni di incipiente scivolamento

g N

a_h = ' . Si ottengono le seguenti espressioni: ⋅

(

−

)

⋅ + ⋅

(

δ +β

)

= 1 kv Ww PAE sin Q

(

)

w AE N W P T = ⋅cosδ +β + '⋅ b Q T = ⋅tanδ

Sostituendo a PAE l’espressione ricavata con il metodo di Mononobe-Okabe (3.10) si

ottiene:

(

)

(

)

[

]

' tan tan sin cos 2 1 2 N K H W b b AE w − ⋅ + − + ⋅ ⋅ ⋅ ⋅ = δ δ δ β δ β γ

con KAE coefficiente di spinta attiva dinamico valutato tramite la (3.11) nella quale si sia

posto kh pari a N’. Nel caso di kv =0, l’espressione precedente può essere espressa in funzione dell’accelerazione limite N:

(

)

(

)

[

]

N K H W b b AE w ₋ ⋅ + − + ⋅ ⋅ ⋅ ⋅ = δ δ δ β δ β γ tan tan sin cos 2 1 2

Attraverso la (3.32), N risulta funzione oltre che del peso del muro e delle sue caratteristiche geometriche, anche della resistenza al taglio del terreno e dell’attrito muro-terreno.

Utilizzandola in combinazione con la (3.27), essa consente di risolvere due problemi di rilevante interesse pratico:

• Ricavare il peso del muro Ww in grado di assicurare il rispetto di un prefissato

valore di spostamento ammissibile D per il sisma di progetto assunto (kh)

• Ricavare il coefficiente sismico N da adoperare nelle verifiche di stabilità pseudo-statiche di un muro con il metodo di Mononobe-Okabe in modo che,

(3.31) (3.30) (3.29) (3.28)

sotto l’azione del sisma di intensità attesa (kh), venga assicurato il rispetto di un

prefissato valore di spostamento ammissibile D. In tal caso si utilizza la (3.27) per ricavare N e si determina il peso Ww con le verifiche previste dall’analisi

pseudo-statica utilizzando il valore di KAE ottenuto dalla (3.10) con kh =N.

3.3.3 Metodo delle tensioni

Il metodo pseudo-statico e il metodo degli spostamenti si basano su considerazioni di equilibrio limite, in altre parole il comportamento del terreno è ipotizzato di tipo rigido-plastico. Essi assumono che gli spostamenti subiti dall’opera siano in grado di assicurare il raggiungimento di condizioni plastiche di rottura nel terreno. Quando questi spostamenti non possono essere raggiunti, la determinazione delle pressioni laterali comporta la risoluzione di un complesso problema di valori al contorno in campo dinamico per il quale sono richieste:

• la conoscenza delle caratteristiche di rigidezza dell’opera • l’assunzione di un modello costitutivo del terreno

• la definizione delle condizioni al contorno • la determinazione dello stato tensionale iniziale • la conoscenza della completa “time history” del sisma

Per poter seguire in maniera più accurata l’interazione tra terreno e opera di sostegno si fa abitualmente ricorso a codici di calcolo. Essi utilizzano metodi numerici per la soluzione, il cui obiettivo principale è sempre quello di determinare le caratteristiche della sollecitazione nel sistema di sostegno per il dimensionamento strutturale. In aggiunta a questo, le analisi numeriche sono anche condotte per valutare gli spostamenti della struttura e, quando possibile, del terreno intorno e al di sotto del piano di scavo.

3.3.3.1 Modellazione del terreno

Le analisi possono essere condotte a diversi livelli di complessità. Le analisi più semplici sono quelle in cui il terreno viene assimilato ad un letto di molle orizzontali indipendenti o con qualche interconnessione, conosciuto come sottosuolo alla Winkler.

di forze nei contrasti; per quanto riguarda gli spostamenti forniscono quelli della struttura mentre non danno informazioni su quello che avviene a distanza dal piano di scavo. Analisi più complesse sono invece i cosiddetti modelli di continuo che comprendono soluzioni agli elementi finiti, alle differenze finite e agli elementi al contorno. Nei metodi agli elementi finiti, la geometria del terreno ed il sistema di vincolo sono approssimati da elementi discreti mentre in quelli alle differenze finite il mezzo continuo è suddiviso in aree comprese tra punti regolarmente spaziati. L’obiettivo di queste analisi è di valutare l’entità degli spostamenti non solo in corrispondenza della struttura ma anche ad una certa distanza intorno e al di sotto del piano di scavo, allo scopo di controllare che gli spostamenti indotti nelle strutture adiacenti siano abbastanza piccoli da non produrre danni strutturali.

Il livello di complessità delle analisi numeriche deve essere adeguato al problema progettuale in esame. Se il deposito è fortemente eterogeneo, è difficile che l’indagine geotecnica sia sufficiente a determinare con certezza le condizioni del sottosuolo. In questo caso può essere sufficiente eseguire un certo numero di analisi con sottosuolo alla Winkler finalizzate a determinare l’intervallo di variazione delle caratteristiche della sollecitazione e delle forza nei puntoni o negli ancoraggi. Se invece non vi sono significative variazioni delle proprietà del deposito in direzione orizzontale, la scelta di eseguire analisi più complesse è giustificata.

Nella maggior parte dei problemi progettuali, è consigliabile impiegare la modellazione matematica più semplice possibile per il terreno, sufficiente ad ottenere risultati adeguati. I modelli costitutivi comunemente adottati per il terreno nei metodi di analisi agli elementi finiti comprendono:

• modello elastico lineare isotropo • modello elastico lineare anisotropo

• modello elastico lineare perfettamente plastico (con criterio di resistenza di Mohr-Coulomb)

• modello elastico non lineare perfettamente plastico

Il comportamento del terreno può essere analizzato sia in termini di tensioni totali che in termini di tensioni efficaci e in quest’ultimo caso le analisi possono essere condotte in condizioni drenate o non drenate, o tenendo conto della consolidazione accoppiata.

Il numero e il tipo di parametri richiesti dipende dal modello costitutivo adottato per il terreno e cresce con la complessità del modello stesso. Il modello Mohr-Coulomb può essere considerato un’approssimazione di primo ordine del comportamento reale dei terreni. Questo modello elastico perfettamente plastico richiede cinque parametri fondamentali, e cioè il modulo di Young E, il coefficiente di Poisson ν, la coesione c, l’angolo di attrito φ e l’angolo di dilatanza ψ.