I
Ringraziamenti
La presente tesi `e stata svolta presso i laboratori della C.A.E.N. S.p.A., nella sede di Viareggio in Via Vetraia n. 11, nel periodo compreso tra maggio 2008 e maggio 2009.
Desidero esprimere la mia gratitudine alla direzione dell’azienda per avermi consentito di effettuare a coronamento del mio curriculum di studi, questa interessante esperienza applicativa a diretto contatto con una realt`a industriale all’avanguardia.
Un particolare ringraziamento va all’Ing. Carlo Tintori per l’assistenza, le discussioni, i suggerimenti e la pazienza profusi nel corso di tutte le fasi che hanno caratterizzato l’attivit`a di tesi.
Sono altres`ı indebitato nei confronti dell’Ing. Andrea Pezzini per avermi gentilmente introdotto all’ambiente C.A.E.N.
Un sincero ringraziamento `e diretto anche a tutti i ragazzi della sezione di Front End che si sono spesi in maniera illuminante nelle (ahim´e!) frequenti richieste di consulenza tecnico-informatica.
Con analoga riconoscenza ringrazio il prof. Diego Passuello che ha saputo imprimere a questo lavoro una forma pi´u adeguata attraverso un acuto lavoro di correzione del manoscritto.
Impossibile esprimere con parole la gratitudine che sento di riconoscere alla mia famiglia senza il cui inestimabile contributo questo lavoro non si sarebbe potuto completare: a mio padre, la cui profonda conoscenza e intelligenza hanno saputo guidarmi nel com-prendere ci`o che stavo facendo; a mia madre, per l’indispensabile affetto di cui mi ha costantemente circondato.
Indice
Introduzione V
1 Descrizione del sistema 1
1.1 Sistema analogico . . . 1
1.1.1 Rivelatore . . . 1
1.1.2 Preamplificatore . . . 3
1.1.3 Filtro Formatore . . . 6
1.2 Digitalizzazione del sistema . . . 9
1.2.1 Digitalizzazione e rilevazione di picco . . . 9
1.2.2 Digitalizzazione e analisi dell’impulso . . . 10
2 Stima congiunta di ritardo e ampiezza 11 2.1 Stima a massima verosimiglianza . . . 11
2.1.1 Modello del segnale . . . 11
2.1.2 Derivazione dello stimatore congiunto MV . . . 13
2.2 Precisioni ottenibili: limite di Cramer-Rao . . . 15
3 Problematiche di digitalizzazione 19 3.1 Frequenza di campionamento . . . 19
3.2 Stima della forma impulsiva dei dati sperimentali . . . 22
3.3 Tecniche di interpolazione . . . 22
3.3.1 Interpolazione parabolica . . . 24
3.3.2 Interpolazione spline cubica . . . 26
3.3.3 Interpolazione con funzioni kernel a banda limitata . . . 28
3.3.4 Grafici di confronto . . . 34
4 Risultati di simulazione e sperimentali 39 4.1 Sistema simulato . . . 39
4.1.1 Condizioni di simulazione . . . 39
4.1.2 Prestazioni di stima sui segnali simulati . . . 41
4.2 Sistema sperimentale . . . 42 III
4.2.2 Prestazioni di stima sui segnali sperimentali . . . 42
5 Riepilogo e conclusioni 45
6 Appendice A: Calcolo di due BCR 47
6.0.3 Esempio 1: impulso gaussiano . . . 47 6.0.4 Esempio 2: impulso esponenziale decrescente smussato . . . 49
7 Appendice B: Software sviluppato 53
7.1 Interpolazione tramite curve Spline cubiche . . . 53 7.2 Interpolazione tramite funzioni kernel a banda limitata . . . 59 7.3 Simulazione di impulsi . . . 62
Introduzione
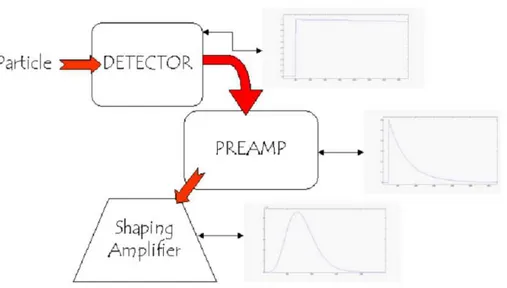
Le moderne tecniche spettroscopiche applicate alla Fisica delle particelle (ad es. per l’identificazione dei prodotti di decadimento delle reazioni nucleari) richiedono comune-mente l’impiego di opportuni sistemi di rivelazione. Lo studio di sensori e di congegni preposti al suddetto scopo ha prodotto durante gli anni una vasta letteratura scientifica ricca di esempi su tale argomento. In linea generale per sistema di rivelazione si intende un complesso costituito da elementi sensibili al passaggio di radiazioni ionizzanti; tale complesso ha la funzione di convertire l’energia depositata dalle particelle incidenti in impulsi di corrente, i quali, dopo opportuna amplificazione e condizionamento elettronico, possono essere inviati ad un’unit`a di elaborazione avente lo scopo di misurare alcuni dei parametri relativi agli impulsi raccolti, tra i quali uno dei pi´u rilevanti `e la carica q, legata all’energia posseduta dalla particella incidente. Altri parametri di interesse scientifico possono essere l’istante di arrivo della particella, la distribuzione temporale degli arrivi, la forma dell’impulso, ecc..
La stima delle grandezze ora menzionate `e affetta da errori legati sia al tipo di trattamento del segnale (ad esempio, se analogica o digitale), sia alle incertezze nella conoscenza dei parametri che caratterizzano il dispositivo stesso di misura (ad esempio, risposte impulsive, guadagni ecc..), sia infine alla presenza di disturbi (quali il rumore termico, il rumore di quantizzazione per le implementazioni digitali ecc.) che si sommano al segnale utile degradando inevitabilmente le prestazioni di qualsiasi algoritmo di stima. La presente tesi `e stata interamente svolta presso la C.A.E.N. S.p.A. di Viareggio, azienda specializzata nella produzione di strumentazione elettronica di Front End e Power Supply per laboratori di fisica delle particelle, e tratta un tema di specifico interesse per tale azienda. Una tipica catena d’acquisizione prodotta da C.A.E.N. `e costituita da stadi di elaborazione del segnale che, posizionati a valle del Detector, effettuano operazioni di preamplificazione e di formatura del segnale stesso (Preamplifier e Shaping amplifier); l’uscita del suddetto stadio viene inviata ad un rivelatore di picco (Peak-Sensing), allo stato attuale elemento cardine per la misura dell’ampiezza degli impulsi in ingresso. L’ampiezza in uscita a tale rivelatore (che `e un dispositivo di tipo analogico) viene “letta” a mezzo di uno stadio di conversione analogico-digitale (A/D), per poi essere memorizzata e resa disponibile per le necessarie elaborazioni in tempo reale o off-line su PC.
Il punto di partenza della tesi `e stato quello di eliminare il rivelatore di picco analogico
tore di Shaping, con la conseguente necessit`a di sostituire operazioni che prima venivano effettuate in analogico (nella fattispecie la citata rivelazione di picco) con operazioni implementate via software off-line oppure su FPGA (Field Programmable Gate Array) . Pi´u ambiziosamente, la citata modifica offre la possibilit`a, non perseguibile nella versione del sistema impiegante il rivelatore di picco analogico, di valutare parametri e statistiche aggiuntive degli impulsi di ingresso tali da rivestire un sicuro interesse per lo studio delle propriet`a delle particelle incidenti sul detector, quali i loro istanti di arrivo, la loro frequenza media di presentazione ecc.; inoltre un’opportuna elaborazione digitale del segnale consente di effettuare tali stime in modo ottimale, ad esempio in accordo al criterio di minimizzazione dell’errore quadratico medio. A tale riguardo si fa osservare che la stima dell’ampiezza degli impulsi, che con l’impiego del rivelatore di picco analogico viene effettuata misurando il valore di picco assoluto della forma d’onda in uscita all’amp-lificatore di shaping - con la conseguenza che insieme all’ampiezza desiderata si va a misurare anche il valore del rumore istantaneamente presente su di essa senza tentarne in alcun modo la riduzione - pu`o essere effettuata con maggiore accuratezza sfruttando la conoscenza della forma dell’impulso (che `e nota o rilevabile sperimentalmente off-line con notevole precisione) e facendo ricorso ad una specifica tecnica di elaborazione del segnale nota come cross-correlazione. Quest’ultima consiste nel far “scorrere” temporalmente una versione locale, normalizzata in ampiezza e priva di rumore, dell’impulso “campione” prodotto dall’amplificatore di shaping lungo il segnale rumoroso osservato e, per ogni posizione relativa τ tra queste due forme d’onda, nel calcolare l’integrale del loro prodotto: `e intuitivo che il valore dell’integrale risulter`a massimo in stretta prossimit`a del valore di
τ per il quale l’impulso locale si trovi allineato con quello rumoroso osservato.
Rimandando ai capitoli seguenti una discussione approfondita dell’algoritmo, ci si limita per il momento a ricordare che tale tecnica consente la stima congiunta efficiente sia del ritardo di arrivo che dell’ampiezza dell’impulso osservato quando quest’ultimo `e affetto da rumore gaussiano con spettro di potenza uniforme (o “bianco”), con il termine “efficiente” intendendosi una stima non polarizzata (ovvero con errore a media statistica nulla) e con varianza dell’errore tendente al bound di Cramer-Rao, vale a dire, al limite inferiore invalicabile alla varianza di qualunque stimatore non polarizzato.
La digitalizzazione del segnale immediatamente a valle dell’amplificatore di shaping comporta il dover affrontare e risolvere un certo numero di problemi, il primo dei quali attiene al dimensionamento della stessa procedura di digitalizzazione. Anche in questo caso sono presenti differenze sostanziali rispetto al sistema impiegante il rivelatore di picco analogico: infatti quest’ultimo segue rapidamente il segnale di ingresso durante i suoi fronti di salita, ma fornisce alla sua uscita un livello costante quando il segnale decresce o ha valore inferiore a quello massimo gi`a incontrato. Prescindendo dagli occasionali transitori di salita, pertanto, il segnale in uscita dal rivelatore rimane prevalentemente costante e quindi non presenta particolari problemi di conversione A/D, specie se lo scopo dello strumento `e quello di utilizzare proprio i tratti costanti per misurarne il livello.
VII Al contrario, dovendo convertire in digitale il segnale in uscita all’amplificatore di shaping in modo da conservarne intatto il contenuto informativo, `e prima di tutto neces-sario assicurare che la cadenza di campionamento adottata sia adeguatamente superiore al doppio della banda del segnale osservato, allo scopo di garantire che la sequenza di campioni ottenuta non sia affetta da fenomeni di “aliasing”, ovvero di ripiegamento spettrale [2], che degraderebbero le prestazioni del cross-correlatore. Un secondo problema che si incontra `e relativo alla quantizzazione dei campioni prelevati, ovvero al numero di bit su cui si effettua la digitalizzazione, che deve essere non troppo piccolo per poter trascurare gli errori di troncamento o quantizzazione rispetto alle altre sorgenti di errore, ma nemmeno troppo grande per contenere la complessit`a ed il costo dell’hardware digitale. Fortunatamente, come sar`a evidenziato in seguito, i dispositivi di conversione A/D dis-ponibili in C.A.E.N. sono sufficientemente veloci ed accurati da consentire di superare entrambe le suddette problematiche progettuali senza incorrere in degradazioni apprezza-bili.
Un ulteriore aspetto da considerare nello studio del nuovo sistema `e ancora legato alla discretizzazione temporale che caratterizza i segnali dopo la conversione A/D: volendo valutare contemporaneamente il valore di picco e il tempo di arrivo degli impulsi con una precisione migliore rispettivamente del passo di quantizzazione e dell’intervallo di campionamento, `e inevitabile fare ricorso a tecniche di interpolazione, la cui accuratezza deve essere tale da non peggiorare apprezzabilmente gli errori presenti sulle stime di ampiezza e ritardo rispetto a quanto gi`a non lo sarebbero per effetto del solo rumore in una situazione ipotetica caratterizzata da errore di quantizzazione nullo e frequenza di campionamento infinita. Pi´u specificatamente, la versione digitale della procedura di cross-correlazione sopra menzionata richiede l’impiego di sommatorie al posto degli integrali e conduce ad una sequenza a ritardi discreti nel dominio τ , con spaziatura pari all’intervallo di campionamento. Tale successione di valori rappresenta un campionamento della funzione di cross-correlazione analogica (ottenuta con gli integrali), e partendo da essi `e necessario andare ad individuare per interpolazione la posizione ed il valore del picco di tale cross-correlazione “sottostante” ai campioni. Data la rilevanza di tali problemati-che, una parte non trascurabile del presente lavoro `e dedicata all’analisi ed al confronto di alcune tecniche di interpolazione.
L’organizzazione della tesi `e la seguente: nel successivo capitolo 1 si descrivono la struttura e le funzioni sia della catena spettroscopica nella sua attuale configurazione che del sistema nuovo specificando anche opportuni modelli per gli impulsi e per il rumore ad essi sovrapposto. Nel capitolo 2 si affronta il problema teorico della stima ottima congiunta del tempo di arrivo e dell’ampiezza di un impulso immerso in rumore gaussiano bianco, evidenziandone anche le prestazioni massime raggiungibili (limite di Cramer-Rao). Il capitolo 3 `e dedicato alla discussione delle problematiche legate alla digitalizzazione del segnale in uscita all’amplificatore di shaping, iniziando dalla scelta della frequenza di campionamento e della precisione dell’aritmetica, proseguendo con la stima da dati sperimentali della forma d’onda impulsiva “campione” prodotta dall’amplificatore e
finen-`e dedicato alla presentazione e alla discussione dei risultati di simulazione e sperimentali: in particolare, in esso si quantificano i vantaggi legati al nuovo approccio in termini di maggiore precisione ottenibile nella stima del picco dell’impulso.
Tutti i risultati qui presentati, in relazione all’elaborazione sia di segnali acquisiti sperimentalmente che generati per simulazione, sono stati ottenuti a mezzo di software sviluppato ad hoc in ambiente C ++ e Matlab, del quale si forniscono i sorgenti in appendice.
Capitolo 1
Descrizione del sistema
1.1
Sistema analogico
Un sistema per misurazioni spettroscopiche `e in genere costituito da un primo blocco analogico seguito da un convertitore analogico-digitale a sua volta interfacciato con un’u-nit`a di elaborazione; il blocco analogico riceve direttamente dal detector gli impulsi di carica di cui si desidera valutare alcuni parametri (energia, massa, ecc.) ed ha la funzione di tradurre la perturbazione che avviene nella regione di rivelazione in un segnale elettrico misurabile. Una configurazione tipica di tale struttura `e idealmente riportata in figura 1.1.
1.1.1
Rivelatore
Il rivelatore `e il primo elemento costitutivo di una catena spettroscopica. Genericamente presenta una regione centrale sensibile al passaggio di radiazioni (termine con cui si identificano particelle cariche cos`ı come onde elettromagnetiche); la radiazione incidente interagisce con la materia presente in questa zona provocando, nel caso ad esempio di una camera a ionizzazione, fenomeni di ionizzazione in proporzione all’energia depositata. La carica prodotta viene raccolta, ad esempio sulle facce di un condensatore, ai capi del quale si viene cos`ı a manifestare una variazione di potenziale elettrico di valore legato all’energia della radiazione entrante.
La letteratura scientifica comprende numerosi esempi di sistemi di rivelazione classi-ficabili in primo luogo per il tipo di interazione tra la radiazione incidente e la materia contenuta nella zona attiva.
Per effettuare un’analisi quantitativa del processo di rivelazione `e opportuno ricorrere ad una modellizzazione elettrica comunemente adottata: infatti si pu`o modellizzare il rivelatore come un generatore di corrente (I) chiuso su un’impedenza risultante dal parallelo di una resistenza Rdcon una capacit`a Cd; il valore da attribuire a questi elementi
Figura 1.1: Sistema analogico.
circuitali dipende dalle modalit`a con cui `e stato costruito il rivelatore. In figura 1.2 `e riportato lo schema circuitale del sistema di rivelazione.
Un impulso di carica acquisito dal rivelatore viene tradotto in una variazione della tensione ai capi del condensatore proporzionale al valore della carica transitata. Succes-sivamente il sistema si riporta verso lo stato di equilibrio iniziale tramite un processo di scarica del condensatore.
Modellando l’impulso di corrente come una delta di Dirac l’evoluzione del circuito `e descritta nel dominio della frequenza dalla seguente equazione
VCd(ω) =
Rd
1 + iωCdRd
q (1.1)
dove q `e la carica prodotta dal passaggio della particella. Antitrasformando l’espressione 1.1 si trova
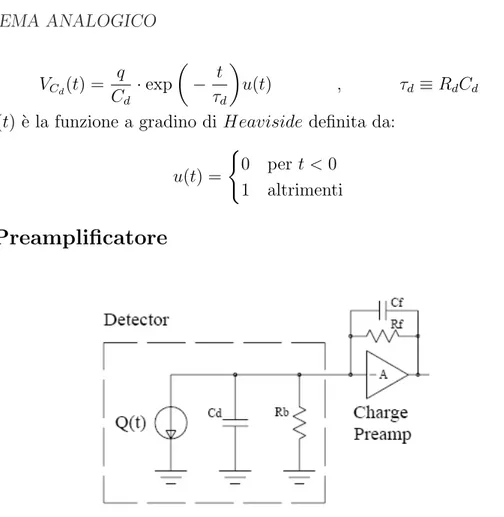
1.1. SISTEMA ANALOGICO 3 VCd(t) = q Cd · exp µ − t τd ¶ u(t) , τd ≡ RdCd
dove u(t) `e la funzione a gradino di Heaviside definita da:
u(t) =
(
0 per t < 0 1 altrimenti
1.1.2
Preamplificatore
Figura 1.3: Cascata del detector seguito da uno stadio di preamplificazione.
Conoscendo con precisione il valore della capacit`a equivalente del rivelatore Cd
potrem-mo fornire una stima dell’ energia depositata dalla particella semplicemente misurando l’ampiezza del gradino q/Cd. In pratica il valore di Cd `e legato ad una moltitudine di
parametri fisici (escursioni di temperatura, variabilit`a del potenziale di polarizzazione delle giunzioni interne al rivelatore) i quali, oltre che variabili, non sono sotto il controllo diretto dello sperimentatore; ne consegue che il valore della capacit`a equivalente attribuibile al detector fluttua inevitabilmente in modo incontrollabile, impedendo una misura oggettiva della carica q.
Per ovviare a questo inconveniente si collega il detector in serie ad un amplificatore operazionale in configurazione invertente (fig. 1.3). Il suddetto dispositivo viene realizzato in modo che la sua impedenza d’ingresso sia molto alta (si ottiene inserendo un transistor ad effetto di campo come stadio di input); in questo modo la corrente non `e assorbita dall’operazionale ma risulta convogliata quasi interamente sul carico di feedback. Inoltre la tensione di uscita (sempre che si rimanga nell’ambito del comportamento lineare dell’o-perazionale) `e proporzionale alla tensione di ingresso tramite un fattore moltiplicativo
un’impedenza d’ingresso infinita, possiamo scrivere la seguente equazione complessa per la tensione nel ramo di feedback:
ˆ
Vout(ω) = − ˆI(ω)Z(ω) = ˆIin(ω)
Rf
1 + iRfCfω
(1.2)
dove Z(ω) indica l’impedenza del blocco di reazione Rf − Cf. Il risultato ottenuto
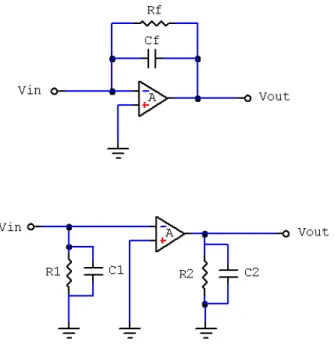
pu`o essere riformulato trasformando il sistema di figura 1.3 tramite il teorema di Miller [1]: l’impedenza di feedback pu`o essere sostituita idealmente da due componenti distinte applicate rispettivamente all’ingresso (Z1) e all’uscita (Z2) dell’amplificatore, come indicato
in fig.1.3; esplicitando le equazioni di maglia per il nuovo circuito e integrandole con le equazioni del vecchio si ottengono le seguenti condizioni sui valori delle impedenze sostitutive:
Figura 1.4: Circuito amplificatore in configurazione invertente e il suo equivalente per
effetto Miller. Z1 = Zf 1 + A Z2 = A A + 1Zf (1.3)
Nel caso che l’ impedenza di feedback sia puramente resistiva pu`o essere sostituita con una resistenza R1 applicata all’ingresso di valore
1.1. SISTEMA ANALOGICO 5
R1 =
1
1 + ARf ∼ 0 essendo |A| À 1; nel caso di un’impedenza capacitiva si ottiene
C1 = (1 + A)Cf À Cd.
L’ultima espressione ci permette di concludere che il posizionamento di un amplificatore operazionale in serie al detector consente di convogliare sulla capacit`a equivalente C1 la
maggior parte della carica libera accumulata nel rivelatore. In questo modo il valore della tensione di uscita `e proporzionale alla quantit`a di energia depositata nel detector indipentemente dalle imprevedibili fluttuazioni nel valore della capacit`a Cd.
Per calcolare teoricamente la tensione in uscita dal preamplificatore `e necessario co-noscerne la funzione di trasferimento, quindi la composizione interna dell’operazionale. Senza approfondire la trattazione su dettagli circuitali si riporta di seguito la generica funzione di trasferimento per un amplificatore operazionale a polo dominante:
HOpAmp=
αOA
1 + iτ ω (1.4)
Il termine τ corrisponde all’inverso della frequenza angolare di taglio dell’amplificatore e αOA `e un fattore moltiplicativo adimensionale caratteristico.
Tenendo conto dell’ aggiunta della rete di feedback caratterizzata dall’impedenza complessa:
Zf =
Rf
1 + iRfCfω
si giunge, dopo una lunga serie di calcoli, all’espressione della funzione di trasferimento per il blocco detector-amplificatore nel caso che la tensione sia di tipo impulsivo a δ di Dirac. ˆ Vout = q iωCf · iωτf 1 + iωτf · 1 1 + iωτr τr¿ τf (1.5)
dove τr `e legata alla costante temporale τ dalla relazione
τr =
τ αOA
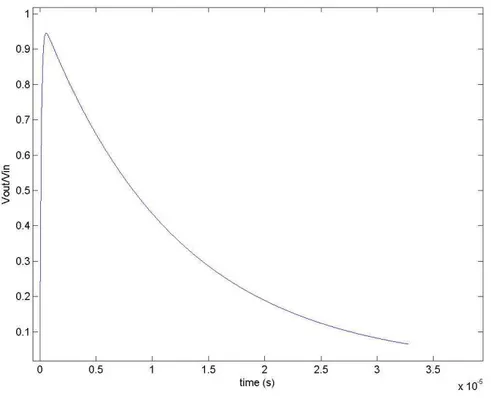
La precedente equazione rappresenta la funzione di trasferimento di un filtro integratore seguito da un filtro derivatore e da un filtro passa-basso ( quest’ultimo caratterizzato da una frequenza di taglio pari a 1/τr). Antitrasformando l’espressione 1.5 si ottiene
l’andamento della tensione all’uscita del premplificatore
esplicitata in 1.6. In figura 1.5 `e stato riprodotto tale andamento.
Figura 1.5: Risposta impulsiva della cascata detector-preamplificatore.
1.1.3
Filtro Formatore
La scelta dei componenti interni del preamplificatore viene effettuata in modo che il tempo di decadimento dell’impulso risulti sufficientemente lungo; viene cos`ı garantito il tempo minimo per la raccolta della carica all’interno del detector.
Questa scelta incide sulla misura del picco degli impulsi nel caso in cui la frequenza di ingresso delle particelle sia sufficientemente elevata da non permettere un ripristino totale del sistema al livello di base. Si verifica in tal caso un fenomeno di pile-up: a causa del ristretto intervalllo temporale tra eventi consecutivi pu`o accadere che un impulso si formi quando non si `e ancora del tutto azzerato il precedente; in questa situazione la misura fornisce risultati alterati rispetto ai reali valori dell’energia depositata ( ad es. i valori di picco possono venire sovrastimati).
Inoltre la forma funzionale dell’impulso presenta una sommit`a molto piccata, il che rende complicato misurare con precisione il valore della sua ampiezza.
1.1. SISTEMA ANALOGICO 7 La soluzione di tali problemi richiede dunque l’accorciamento dei tempi di decadimento degli impulsi rispettando contemporaneamente la relazione di proporzionalit`a tra valore di picco e quantit`a di energia depositata nel rivelatore. A tale scopo si elabora il segnale uscente dal premplificatore tramite un filtro analogico formatore (Shaper).
Figura 1.6: Risposta ad un filtraggio di shaping.
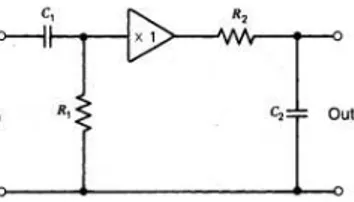
Con riferimento alla figura 1.7, tale filtro viene costruito assemblando resistenze e
Figura 1.7: Filtro di shaping capacit`a con l’obiettivo di “formare” opportunamente
il segnale; in fig.1.7 `e riportata la configurazione pi´u semplice di un filtro del tipo suddetto.
Tipicamente si compone di una rete CR (derivatore) seguita da una rete RC (integratore) eventualmente ripetuta pi´u volte.
L’amplificatore operazionale a guadagno unitario viene detto separatore ed `e idealmente interposto tra i due elementi per garantire che le varie sezioni di filtraggio non si carichino vicendevolmente.
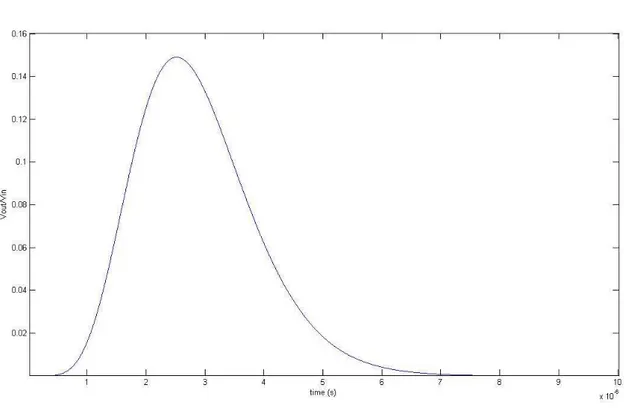
temporali identiche) dallo schema di fig. 1.7 si ottiene un filtro che ha una risposta del tipo Vout= Vint τe −t τ (1.7)
il cui andamento `e illustrato in fig. 1.6.
Figura 1.8: Risposta ad un filtraggio semigaussiano per n = 7.
Se nella catena illustrata in figura 1.7 inseriamo ulteriori stadi di tipo RC otteniamo un segnale di uscita che approssima maggiormente una funzione di tipo gaussiano. Si parla in questo caso di filtraggio semi-gaussiano; con n stadi RC in cascata allo stadio
CR si ottiene una risposta ad un impulso a gradino del tipo Vout = Vin µ t τ ¶n e−τt · 1 n! (1.8)
il cui grafico `e rappresentato in fig. 1.8 per n = 7 che rappresenta il caso dello Shaper implementato nella scheda MOD.N968 attualmente prodotta da CAEN.
1.2. DIGITALIZZAZIONE DEL SISTEMA 9
1.2
Digitalizzazione del sistema
Figura 1.9: Modulo N968. Al suo interno
sono implementati un filtro formatore e un circuito di rilevazione di picco.
In questa sezione si introduce l’ultimo stadio della catena spettroscopica, quello cio`e deputato alla digitalizzazione del segnale e alla sua successiva elaborazione. L’output prodotto dalla sezione precedente (Shaping Amplifier) viene digitalizzato, ovvero campionato ad una frequenza di sampling che soddisfi il teorema di
Nyquist e quantizzato ad un numero N
di bit. Questo processo ha l’obiettivo di consentire l’elaborazione digitale del segnale con la possibilit`a di applicare algoritmi pi´u sofisticati nella misura dei parametri d’interesse e di effettuare analisi statistiche sui segnali osservati.
1.2.1
Digitalizzazione e
rile-vazione di picco
L’attuale implementazione della catena spettroscopica utilizzata presso CAEN prevede l’estrazione del valore di picco del segnale tramite l’impiego di un circuito di Peak-Sensing analogico. Non `e scopo di questo lavoro fornire indicazioni dettagliate sul funzionamento di tale circuito; `e sufficiente sapere che il valore dell’ampiezza del segnale viene memorizzato e progressivamente aggiornato man mano che questo cresce. Quando l’impulso oltrepassa la sommit`a e comincia a decrescere il valore massimo viene mantenuto costante tramite un circuito denominato Stretcher, per essere quindi inviato ad un digitalizzatore che ne
restitui-1.2.2
Digitalizzazione e analisi dell’impulso
Lo scopo dell’attivit`a sperimentale di questo lavoro di tesi `e stato caratterizzare un sistema di elaborazione sostitutivo di quello attuale.
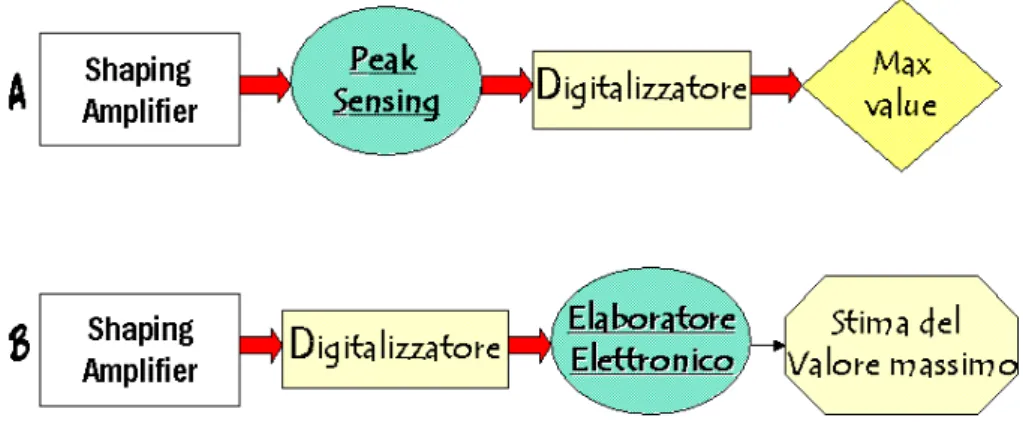
Nella figura 1.10 si confrontano i due approcci sopra descritti mediante uno schema a blocchi funzionali: le operazioni svolte precedentemente dal circuito di peak-sensing vengono, secondo la nuova impostazione, realizzate da un elaboratore elettronico che raccogliendo il segnale formato ne valuta le quantit`a di interesse a seguito di una serie di opportune elaborazioni matematiche. Lo studio di tali tecniche e la messa a punto di algoritmi di Signal processing ad hoc costituiscono il nucleo concettuale di questo lavoro di tesi, pertanto verranno approfonditi in dettaglio nei capitoli successivi.
Figura 1.10: Rappresentazione grafica di due possibili stadi di digitalizzazione ed elaborazione del segnale in una catena spettroscopica. In particolare B riflette l’approccio concettuale adottato nel corso dell’attivit`a sperimentale.
Capitolo 2
Stima congiunta di ritardo e
ampiezza
In questa sezione si delineano i presupposti teorici sui quali si basano gli algoritmi di elaborazione del segnale impiegati nell’attivit`a sperimentale. Viene affrontata la proble-matica della stima contemporanea di due variabili riferendosi nel caso specifico al ritardo di presentazione e all’ampiezza degli impulsi, e viene infine riportato il calcolo teorico del limite inferiore per le precisioni ottenibili nella procedura di stima.
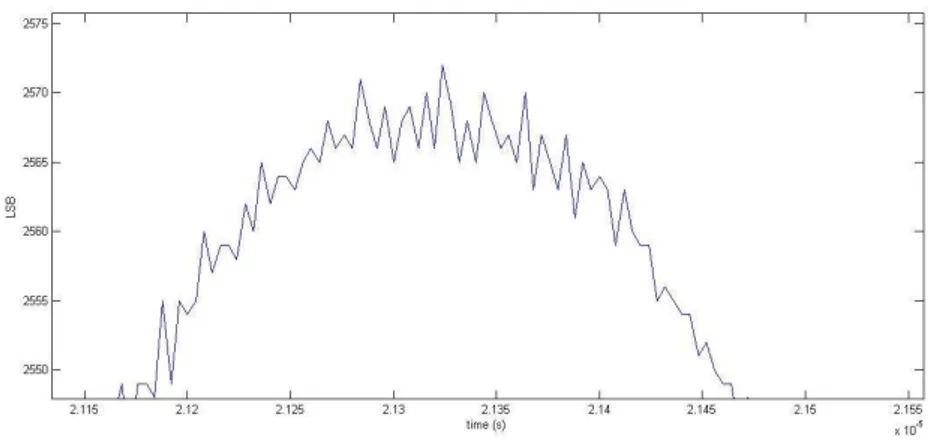
Figura 2.1: Ingrandimento della sommit`a di un segnale osservato.
2.1
Stima a massima verosimiglianza
2.1.1
Modello del segnale
Nei prossimi paragrafi si far`a riferimento al segnale espresso nella seguente forma:
x(t) = Ag(t − τ ) + w(t), t ∈ (0, Toss) (2.1)
dove g(t) `e un impulso di forma nota (ad es. la risposta di un filtro formatore) e valore di picco normalizzato all’unit`a, di durata tale da risultare interamente contenuto nell’intervallo di osservazione (0, Toss), A `e un fattore moltiplicativo (ampiezza) che
de-termina l’energia associata all’impulso osservato, w(t) `e espressione del rumore additivo, considerato gaussiano bianco di livello spettrale bilatero N0/2, infine τ `e il ritardo di
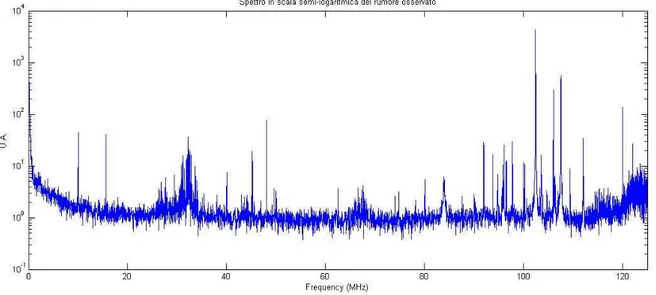
arrivo dell’impulso. Sebbene l’ipotesi di rumore bianco non sia esattamente verificata in pratica essa pu`o ritenersi una ragionevole approssimazione in considerazione di: i) la banda del rumore `e molto pi´u larga di quella del segnale utile (vedi fig. 2.1 che presenta un ingrandimento del picco di un segnale sperimentale in cui sono ben evidenti le fluttuazioni tipiche del rumore), ii) lo spettro effettivo del segnale (un cui esempio `e visibile in figura 2.2) `e caratterizzato su tutta la banda da una molteplicit`a di righe spettrali di ampiezza anche elevata, dovute presumibilmente a sorgenti di interferenza,
iii) le prestazioni dell’algoritmo di stima cui si perviene corroborano, almeno in prima
approssimazione, l’ipotesi suddetta (vedi cap.4).
Figura 2.2: Spettro di potenza del rumore sperimentale osservato.
Sotto l’ipotesi che N0 sia fissato e noto, si desidera individuare la strategia di stima
2.1. STIMA A MASSIMA VEROSIMIGLIANZA 13
2.1.2
Derivazione dello stimatore congiunto MV
Ricorrendo ad una rappresentazione vettoriale dei segnali in un sistema cartesiano or-togonale, indichiamo con x, w e g(τ ) i vettori rappresentativi di x(t), w(t) e g(t − τ ), rispettivamente.
Come `e noto (es. [4]) le componenti di w sono tra loro indipendenti, a media nulla e varianza pari a N0/2; pertanto la densit`a di probabilit`a del vettore osservato
condiziona-tamente ai parametri A e τ `e data da:
p(x; A, τ ) ∝ exp · − 1 N0 ¯ ¯¯¯x − Ag(τ)¯¯¯¯2 ¸ (2.2)
dove il coefficiente davanti all’esponenziale `e stato omesso non avendo rilevanza ai fini della determinazione della strategia di stima.
Si ricorda infatti che il principio di stima MV consiste nel ricercare il massimo della funzione 2.2 interpretata come funzione dei parametri di tentativo ˜A e ˜τ e nella quale il
vettore delle variabili x sia sostituito con il vettore osservato; tale funzione viene detta
funzione di verosimiglianza e la posizione del suo massimo viene assunta come la stima
( ˜AM V, ˜τM V) per A e τ :
( ˜AM V, ˜τM V) = arg max Λ( ˜A, ˜τ ) A > 0, ˜˜ τ ∈ (0, Toss) (2.3)
dove si `e posto Λ( ˜A, ˜τ ) ≡ p(x; ˜A, ˜τ ). Si osserva che il problema di massimizzazione
2.3 `e equivalente a quello della ricerca del massimo del logaritmo naturale di Λ( ˜A, ˜τ ), in
quanto il logaritmo `e funzione monotona crescente del suo argomento. In questo caso si suole parlare di funzione di log-verosimiglianza. Pertanto dalle 2.2-2.3 si pu`o scrivere:
( ˜AM V, ˜τM V) = arg min ||x − ˜Ag(˜τ )||2 A > 0, ˜˜ τ ∈ (0, Toss) (2.4)
dove il coefficiente contenente il parametro N0 visibile nella 2.2 `e stato omesso in
quanto non rilevante ai fini della ricerca del massimo.
L’argomento nell’ultimo termine della 2.4 si pu`o sviluppare come segue:
||x − ˜Ag(˜τ )||2 = ||x||2+ ˜A2E
g− 2 ˜Ax · g(˜τ ) (2.5)
dove si `e definita l’energia (nota) di g(t) come Eg ≡ ||g(˜τ )||2. Si osserva che il primo
termine a secondo membro di 2.5 non dipende da ˜τ e quindi pu`o essere ignorato non
avendo influenza sulla ricerca del minimo; il secondo termine dipende solo da ˜A e non
da ˜τ in quanto l’energia dell’impulso non cambia con la sua posizione purch´e esso (come
ipotizzato all’inizio) sia interamente contenuto entro (0, Toss). Per quanto infine riguarda
il terzo termine, esso consiste nel prodotto di due fattori dipendenti separatamente da ˜A
e ˜τ . Derivando quindi la 2.5 rispetto ai due parametri di tentativo ed eguagliando a zero
˜
AEg− x · g(˜τ ) = 0 (2.6)
∂
∂ ˜τ[x · g(˜τ )] = 0 (2.7)
che mostrano come la minimizzazione 2.4 possa essere condotta in due passi consecutivi, il primo dei quali consiste nella ricerca del massimo del prodotto scalare x · g(˜τ ) al variare
del solo parametro ˜τ ; tale ricerca, descritta sotto in maggior dettaglio, conduce quindi
alla determinazione della stima a massima verosimiglianza del ritardo, ˆτM V. In figura
2.3 viene riportato lo schema a blocchi funzionali dello stimatore di τ . Il secondo passo consiste nell’assumere come stima di A l’espressione seguente:
ˆ
AM V =
x · g(ˆτM V)
Eg
(2.8) Ricordando la 2.5, vale la pena osservare che la stima del valore di picco data dalla 2.8 `e anche quella che minimizza la distanza quadratica tra il vettore osservato e la replica locale dell’impulso una volta che quest’ultimo sia stato riallineato, rispetto al segnale osservato, in accordo alla stima del ritardo ˆτM V.
Figura 2.3: Schema funzionale dello stimatore del ritardo τ .
Tornando alla stima del ritardo il prodotto scalare x · g(˜τ ) si pu`o scrivere in forma
integrale come:
x · g(˜τ ) =
Z Toss
0
x(t)g(t − ˜τ ) d t (2.9) Si osserva che il secondo membro di quest’ultima espressione rappresenta la
cross-correlazione campione tra la forma d’onda osservata x(t) e l’impulso g(t), il cui andamento
`e assunto noto allo stimatore. La stima MV del ritardo viene quindi effettuata traslando nel tempo l’impulso g(t) rispetto al segnale osservato ed andando a cercare il massimo dell’integrale del prodotto 2.9.
2.2. PRECISIONI OTTENIBILI: LIMITE DI CRAMER-RAO 15 Definendo: R(˜τ ) ≡ Z Toss 0 x(t)g(t − ˜τ ) d t (2.10)
la stima di τ viene quindi riformulata come segue:
ˆ
τM V = arg max R(˜τ ) τ ∈ (0, T˜ oss)
2.2
Precisioni ottenibili: limite di Cramer-Rao
Consideriamo una variabile casuale X con la relativa densit`a di probabilit`a pX(θ).
Sup-poniamo inoltre di avere definito una funzione SX (stimatore di X) delle realizzazioni R
(valori misurati di X), tale per cui lo scarto tra tale funzione e la variabile X stessa sia in media statisticamente nullo (assenza di polarizzazione); allora `e possibile specificare un limite inferiore relativamente alla precisione del suddetto stimatore.
Nel caso del processo di stima per un unico parametro si dimostra [4] la validit`a della seguente disuguaglianza, detta disuguaglianza o bound di Cramer-Rao (BCR):
E[(SX(R) − X)2] ≥ Ã E (· ∂ ln pr|x(R|X) ∂X ¸2)!−1 (2.11)
solitamente riportata insieme alla seguente espressione:
E[(SX(R) − X)2] ≥ ½ −E · ∂2ln p r|x(R|X) ∂X2 ¸¾−1 (2.12)
Le espressioni appena scritte sono tra loro equivalenti ed affermano l’impossibilit`a di conoscere il valore di una variabile non polarizzata con una precisione inferiore al limite indicato dalle 2.11-2.12. Al fattore E
(·
∂ ln pr|x(R|X)
∂X
¸2)
ci si riferisce comunemente con il termine informazione di Fisher.
Allo scopo di effettuare il calcolo del BCR nel caso di stima congiunta di pi´u parametri `e necessario calcolare la matrice di Fisher J(A, τ ) [4] (corrispettivo bidimensionale
dell’in-formazione di Fisher nel caso di un solo stimatore), che nel caso in esame `e una matrice
J11(A, τ ) ≡ −Ex;A,τ · ∂2 ∂A2 ln p(x; A, τ ) ¸ = Ex;A,τ (· ∂ ∂A ln p(x; A, τ ) ¸2) (2.13)
J12(A, τ ) ≡ −Ex;A,τ
· ∂2 ∂A∂τ ln p(x; A, τ ) ¸ = Ex;A,τ ½ ∂ ∂Aln p(x; A, τ ) ∂ ∂τ ln p(x; A, τ ) ¾ (2.14) J21(A, τ ) = J12(A, τ ) (2.15)
J22(A, τ ) ≡ −Ex;A,τ
· ∂2 ∂τ2 ln p(x; A, τ ) ¸ = Ex;A,τ (· ∂ ∂τ ln p(x; A, τ ) ¸2) (2.16)
Ricordando l’espressione della densit`a di probabilit`a 2.2 si ha che:
ln p(x; τ ) ∝ − 1 N0 ||x − Ag(τ )||2 = 1 N0 ¡ −||x||2− A2||g(τ )||2+ 2Ax · g(τ )¢ (2.17)
Si osserva che il primo termine dell’ultima espressione non dipende dai parametri da stimare e quindi `e destinato a scomparire a seguito delle derivate presenti nelle 2.13-2.16; il secondo termine dipende solo da A e non da τ in quanto Eg ≡ ||g(τ )||2 rappresenta
l’energia (nota) di g(t − τ ) che non cambia con la posizione dell’impulso nell’intervallo di osservazione purch´e l’impulso stesso (come ipotizzato all’inizio) sia interamente osservato. Infine il terzo termine dipende sia da A che da τ , e si pu`o scrivere cos`ı in forma integrale:
2A N0 x · g(τ ) = 2A N0 Z Toss 0 x(t)g(t − τ ) d t (2.18) Procedendo con il calcolo dei termini della matrice di Fisher, si ha dalla 2.17:
∂2
∂A2 ln p(x; A, τ ) = −
2Eg
N0
da cui, essendo sia Eg che N0 quantit`a note e determinate:
J11(A, τ ) = 2Eg N0 Inoltre si ha: ∂2 ∂A∂τ ln p(x; A, τ ) = − 2 N0 Z Toss 0 x(t) ˙g(t − τ ) d t (2.19) da cui, mediando sul rumore:
2.2. PRECISIONI OTTENIBILI: LIMITE DI CRAMER-RAO 17 Ex;A,τ · ∂2 ∂A∂τ ln p(x; A, τ ) ¸ = −2A N0 Z Toss 0 g(t − τ ) ˙g(t − τ ) d t (2.20) Osservando che l’impulso g(t−τ ) `e interamente contenuto nell’intervallo di integrazione e ricorrendo al teorema di Parseval, si pu`o scrivere:
Z Toss 0 g(t − τ ) ˙g(t − τ ) d t = Z ∞ −∞ g(t) ˙g(t) d t = i 2π Z ∞ −∞ Ω|G(Ω)|2d Ω = 0 (2.21)
dove G(Ω) `e la trasformata di Fourier di g(t), con Ω = 2πf frequenza angolare (rad/s). All’ultimo risultato si perviene osservando che il modulo di G(Ω) ha simmetria pari attorno all’origine, a differenza di Ω che ha simmetria dispari. Raccogliendo quanto sopra si vede che:
J12= J21 = 0
il che indica che le stime di A e di τ sono disaccoppiate, vale a dire, l’incertezza sulla conoscenza di ciascuno dei due parametri non ha alcun effetto sulla precisione di stima dell’altro.
Rimane da calcolare J22(A, τ ). A tale scopo, derivando la 2.17 due volte rispetto a τ
si ha: ∂2 ∂τ2 ln p(x; A, τ ) = 2A N0 Z Toss 0 x(t)¨g(t − τ ) d t e mediando si ha infine: Ex;A,τ · ∂2 ∂τ2 ln p(x; A, τ ) ¸ = 2A2 N0 Z Toss 0 g(t − τ )¨g(t − τ ) d t (2.22) Ricordando nuovamente che l’impulso ritardato g(t − τ ) `e interamente contenuto in (0, Toss) e raccogliendo i risultati ottenuti si perviene a:
J22(A, τ ) = 2ξ
Ex
N0
(2.23) dove si `e introdotto il rapporto segnale-rumore Ex/N0tra l’energia dell’impulso osservato,
data da:
Ex ≡ A2
Z ∞
−∞
g2(t) d t (2.24)
e la densit`a spettrale di potenza del rumore; inoltre nella 2.23 compare il parametro ξ che si pu`o considerare un fattore di forma avente la dimensione dell’inverso di un tempo al quadrato, dipendente dall’andamento dell’impulso osservato:
ξ ≡ − ∞ −∞ g(t)¨g(t) d t Z ∞ −∞ g2(t) d t (2.25)
Invocando il teorema di Parseval, si pu`o anche scrivere:
ξ ≡ − Z ∞ −∞ Ω2|G(Ω)|2d Ω Z ∞ −∞ |G(Ω)|2d Ω (2.26)
Raccogliendo quanto sopra si ha la seguente matrice di Fisher:
J(A, τ ) = µ 2Eg/N0 0 0 2ξEx/N0 ¶ (2.27) dalla quale si possono determinare i BCR per A e τ , che rappresentano un limite inferiore non ulteriormente perfezionabile per la varianza d’errore di qualunque stimatore non polarizzato [4]: BCR(A) = J−1 11 = N0 2Eg = A 2 2 1 Ex/N0 (2.28) BCR(τ ) = J−1 22 = 1 2ξ 1 Ex/N0 (2.29) Per quanto riguarda il bound 2.28, si osserva che esso pu`o porsi agevolmente in forma normalizzata:
BCR(A)/A2 = 1
2 1
Ex/N0
il che stabilisce una relazione molto semplice tra la varianza minima dell’errore relativo ed il rapporto segnale-rumore Ex/N0. Ad esempio, per rapporto segnale-rumore pari a
100 (20 dB), la deviazione standard dell’errore relativo non pu`o mai essere inferiore a circa il 7.1%.
Anche il bound 2.29 si pu`o porre in forma normalizzata rispetto al quadrato di un tempo, ma per ottenere un risultato avente significato operativo occorre calcolare esplicitamente il parametro ξ facendo comparire una misura della durata dell’impulso. In appendice A viene effettuato a titolo esemplificativo il calcolo del fattore di forma, e del relativo BCR, nel caso di impulso gaussiano e di impulso esponenziale decrescente smussato.
Capitolo 3
Problematiche di digitalizzazione
In questo capitolo vengono affrontate alcune problematiche tipiche legate all’elaborazione digitale del segnale in uscita dallo Shaping Amplifier. Inizialmente si sofferma l’attenzione sulla scelta dei valori della frequenza di campionamento e del passo di quantizzazione con cui viene effettuata la conversione analogico-digitale del segnale. Successivamen-te si prende in esame la forma funzionale caratSuccessivamen-teristica dell’impulso e se ne fornisce un’espressione analitica ricavata da misure sperimentali. La terza ed ultima parte del capitolo presenta un confronto ragionato tra alcune tecniche di interpolazione mettendone in evidenza vantaggi e svantaggi relativi, in termini di accuratezza e di complessit`a, quando esse vengano utilizzate a supporto delle misure di ritardo e ampiezza richieste; si conclude questa sezione con alcuni grafici di confronto delle prestazioni dei suddetti algoritmi di interpolazione.
3.1
Frequenza di campionamento
La corretta conversione analogico-digitale del segnale richiede una scelta attenta dei parametri di conversione (in particolare, frequenza di campionamento e numero di bit di conversione) in relazione alla banda e alla dinamica di ampiezza della forma d’onda in ingresso. A tale riguardo CAEN ha accumulato esperienza pluriennale: in particolare il vecchio sistema di elaborazione basato su un dispositivo di digitalizzazione (modulo
N957) con circuito di peak-sensing (vedi cap. 1) incorporato permette di discretizzare il
segnale di ingresso con una cadenza di ∼ 1.25 Ms/s e una precisione pari a 13 bit. Le prestazioni del sistema risultante sono state messe a confronto con una configurazione alternativa, il cui studio `e oggetto della presente tesi, in cui il componente N957 `e stato sostituito dal digitalizzatore V 1720 caratterizzato da una frequenza di campionamento pari a 250 Ms/s e una precisione di quantizzazione di 12 bit.
`
E da osservare che il valore relativamente modesto della cadenza di campionamento adottata nella scheda N957 `e da attribuirsi alle peculiari esigenze funzionali di tale
di ingresso senza alcuna pretesa di memorizzarne la forma o altre caratteristiche di dettaglio. In questo caso `e quindi evidente che i soli requisiti da imporre alla cadenza di campionamento `e che essa sia sufficientemente elevata in modo da consentire di rilevare con sicurezza l’impulso in uscita all’amplificatore di shaping (in altri termini: l’impulso non pu`o durare meno dell’intervallo di campionamento!), e che inoltre uno dei campioni cada in stretta prossimit`a del picco dell’impulso stesso in modo che la sua ampiezza possa ben approssimarsi con l’ampiezza massima. Entrambe queste condizioni possono ritenersi ragionevolmente soddisfatte se all’interno dell’impulso di durata minima cadono almeno alcuni campioni (es. 5 − 6), il che conduce a ritenere idonea tale frequenza di campionamento quando la durata degli impulsi non scende indicativamente al di sotto di alcuni microsecondi.
Viceversa, l’adozione della nuova scheda V 1720, avente velocit`a di conversione netta-mente superiore, permette il raggiungimento di obiettivi assai pi´u ambiziosi, a cominiciare dalla possibilit`a di digitalizzare impulsi molto pi´u brevi (fino a poche decine di nanosecon-di) in modo non soltanto da consentirne la misura del valore di picco, ma da memorizzarne l’andamento temporale senza perdere informazioni, vale a dire, evitando fenomeni di aliasing spettrale che insorgono, come `e noto, quando la frequenza di campionamento `e inferiore al doppio del limite superiore di banda (in Hz) del segnale da convertire.
Nel caso in esame gli impulsi con i quali si ha a che fare hanno forma pressoch´e gaussiana (vedi discussione sul BCR nel caso di impulso esponenziale decrescente smussato nell’appendice A); si osserva anche che la forma della funzione di cross-correlazione utiliz-zata per la stima ottima del ritardo e dell’ampiezza degli impulsi in uscita all’amplificatore di shaping `e ancora pressoch´e gaussiana essendo essa il risultato della convoluzione di due impulsi quasi gaussiani.
Indicando dunque con xa(t) un impulso gaussiano centrato nell’origine dei tempi e
avente deviazione σ, `e noto che la sua trasformata di Fourier Xa(Ω) nel dominio della
frequenza angolare Ω (rad/s) ha anch’essa andamento gaussiano centrato sullo zero, con deviazione σω pari all’inverso di σ [6]:
xa(t) = exp µ − t2 2σ2 ¶ Xa(Ω) = √ 2πσ2exp µ −σ2Ω2 2 ¶ (3.1)
Come si vede, in linea di principio un impulso gaussiano ha durata e banda infinite; `e pertanto necessario introdurre una definizione “pratica” di durata e banda di tale impulso per poter dimensionare la sua digitalizzazione. Una possibilit`a consiste nell’attribuire all’impulso una larghezza (sia nel dominio t che Ω) pari a quella dell’intervallo, centrato intorno all’origine, ai cui estremi il valore dell’impulso si sia ridotto di una quantit`a prefissata rispetto al valore assunto nell’origine, ad esempio 3 dB o 10 dB o altro. A titolo esemplificativo, seguendo questo approccio ed indicando con d la durata (bilatera) a −3 dB di xa(t), si ottiene la seguente condizione.
3.1. FREQUENZA DI CAMPIONAMENTO 21 √ 2 2 = exp µ − d 2 8σ2 ¶ → d = 2σ√ln 2 ≈ 1.665σ (3.2)
Essendo dalla 3.1 σω = 1/σ, ne consegue anche che la banda bilatera D a −3 dB
dell’impulso gaussiano `e data da:
D = 2σω √ ln 2 = 2 √ ln 2 σ ≈ 1.665 σ (3.3)
da cui segue la relazione tra d e D:
D(rad/s) = 4 ln 2 d =
2.773
d (3.4)
Indicando con D1 = D/2 = 2 ln 2/d la banda monolatera a −3 dB dell’impulso, un
criterio ragionevole per effettuare il campionamento di xa(t) `e quello di richiedere che
congiuntamente i) il segnale venga osservato per un intervallo di tempo sufficientemente lungo da rendere trascurabile l’effetto del troncamento delle code, ii) la frequenza di campionamento fc = 1/Tc(in Hz) sia adeguatamente pi´u elevata di D1in modo da rendere
trascurabile il gi`a menzionato effetto di aliasing spettrale. Per quanto riguarda il primo requisito, esso `e in pratica largamente soddisfatto dato che la finestra di osservazione temporale dello strumento di rivelazione `e di gran lunga superiore alla durata degli impulsi generati dall’amplificatore di shaping, mentre la seconda condizione richiede che il parametro Ωc = 2πfc sia scelto adeguatamente pi´u elevato di 2D1. A tale riguardo una
scelta opportuna sembra essere Ωc& 6D1, il che implica che la prima replica spettrale di
aliasing sia attenuata in corrispondenza di Ωc/2 di almeno 27 dB e sulla continua di pi´u
di 100 dB.
Tornando alle caratteristiche del dispositivo CAEN V 1720 per il quale fc= 250 MHz,
la condizione Ωc ≥ 6D1 implica che la massima banda bilatera a −3 db dell’impulso
gaussiano sia pari a Dmax = Ωc/3 = 2π × 83.33 × 106 rad/s, e che quindi la durata
bilatera (a −3 dB) dell’impulso nel tempo non possa (dalla 3.4) scendere al di sotto di
dmin ≈ 5.3 ns. Anche questa condizione sembra essere largamente verificata in pratica,
dato che le durate degli impulsi rilevati dal dispositivo in esame non scendono mai al di sotto di alcune decine di nanosecondi.
Per quanto riguarda la precisione di rappresentazione, il numero di bit utilizzato ha garantito in entrambi i casi una buona discretizzazione dell’ampiezza del segnale in quanto il rumore additivo introdotto dall’operazione di quantizzazione si `e mantenuto sempre molto al di sotto dell’ intensit`a del rumore sovrapposto al segnale osservato. Una stima del livello di rumore osservato - la cui natura `e da attribuire ad una moltitudine di fattori inevitabili ed indipendenti dal controllo dello sperimentatore come l’alimentazione da rete elettrica, il rumore termico, ecc. - `e stata ricavata da elaborazioni sui dati raccolti; ad esempio nel caso in cui si utilizzi il digitalizzatore V 1720 il livello di rumore (incluso quello
meno significativo) di dispersione.
3.2
Stima della forma impulsiva dei dati sperimentali
Come gi`a menzionato, la forma analitica del segnale impulsivo osservato `e determinata dalla struttura circuitale dello Shaping Amplifier ed approssima in maniera pi´u o meno fedele l’andamento di una funzione gaussiana a seconda del numero di componenti RC che vengono concatenati all’interno del filtro. In base a quanto gi`a detto la forma effettiva del segnale impulsivo si pu`o genericamente rappresentare tramite la seguente espressione:
y(t, τ0) = µ t τ0 ¶n e−t/τ0 (3.5)
Non essendo reperibili in CAEN informazioni certe circa l’effettivo valore dei parametri
n e τ0, si `e proceduto alla loro stima a minimi quadrati basata su dati sperimentali. A tale
proposito `e stata effettuata una media su un cospicuo numero di acquisizioni dello stesso impulso, alla quale `e stato poi applicato un algoritmo di fitting non-lineare in ambiente Matlab (fig. 3.1). I campioni del segnale utilizzati per l’operazione di media sono stati raccolti tramite l’uso del digitalizzatore veloce V 1720 (fc = 250 Ms/s) e i valori ottenuti
attraverso il suddetto procedimento sono:
n = 7
τ0 = 107.3 × Tc≈ 429.2ns.
3.3
Tecniche di interpolazione
In questa sezione si intendono valutare le prestazioni di alcuni algoritmi d’interpolazione in termini della precisione intrinseca da essi consentita per la stima della posizione e dell’ampiezza di un impulso a partire dai suoi campioni. Poich´e interessa la loro precisione intrinseca, l’analisi che segue `e effettuata supponendo assente il rumore. L’effetto di quest’ultimo `e gi`a stato analizzato nel cap. 2; qui interessa mettere in evidenza quali siano le condizioni sotto le quali gli errori di interpolazione sono trascurabili rispetto agli errori dovuti al rumore.
Si assume che l’impulso in uscita all’amplificatore di shaping abbia forma gaussiana con picco sull’origine dei tempi, ampiezza massima unitaria e durata controllata dal parametro
3.3. TECNICHE DI INTERPOLAZIONE 23
Figura 3.1: Grafico del segnale mediato con sovrapposto l’andamento della funzione di fit
stimata in ambiente Matlab.
y(t) = exp µ − t2 2σ2 ¶ , t ∈ µ −Toss 2 , Toss 2 ¶ (3.6) dove Toss`e il tempo di osservazione del segnale. Come misura della lunghezza temporale
dell’impulso 3.6 si assume la durata bilatera a −3 dB, gi`a definita dalla 3.2:
d = 2√ln 2σ (3.7)
Ricordiamo che la forma d’onda specificata in 3.6 viene digitalizzata e successivamente elaborata allo scopo di fornire una stima del ritardo e del valore di picco, che ovviamente non sono a priori noti al dispositivo di stima. Si suppone che il blocco ADC (digitalizzatore in fig. 1.10) campioni il segnale 3.6 con cadenza fissata a fc = 1/Tc = 250 MHz; poich´e
il campionatore non `e in alcun modo sincronizzato con il segnale di ingresso, i campioni saranno prelevati agli istanti nTc+ φ, n = −N, · · · , N , dove 2N ≈ Toss/Tc `e il numero
complessivo di campioni osservati, supposto molto grande, e φ `e un ritardo (o “fase”) di campionamento il quale pu`o ritenersi compreso tra −Tc/2 e Tc/2. Fasi di campionamento
a dover essere recuperato, ovvero “stimato”, a mezzo di interpolazione.
La successione di campioni in ingresso al dispositivo di elaborazione (detta anche “successione osservata”) si pu`o quindi scrivere, con ovvio significato dei simboli, come:
yn = y(nTc+ φ) = exp · −(nTc+ φ) 2 2σ2 ¸ , n ∈ (−N, N ), −Tc 2 ≤ φ < Tc 2 (3.8) La 3.8 costituisce anche, per quanto detto, l’ingresso del blocco d’interpolazione, il quale, a partire da tale successione, deve consentire una stima accurata ˆτ della posizione
temporale τ del picco sottostante (che, stante la 3.6, `e assunta sull’origine dei tempi, vale a dire, in τ = 0) nonch´e una stima ˆp della sua ampiezza p (unitaria in accordo alla
3.6: p = 1). Si osserva che l’ipotesi di appartenenza di φ all’intervallo (−Tc/2, Tc/2)
implica che il campione massimo della successione 3.8 sia quello di indice 0; ci`o non toglie validit`a generale ai risultati in seguito riportati, dato che in generale lo stesso tipo di operazioni di interpolazione, con la stessa accuratezza di stima della parte frazionaria di φ e dell’ampiezza del picco, andrebbero effettuate nell’intorno del campione di valore massimo, indipendentemente dalla sua posizione nella successione osservata.
Gli errori di stima sul ritardo e sull’ampiezza del picco sono definiti come differenza tra il valore stimato ed il valore vero:
²τ = ˆτ − τ, ²p = ˆp − p
e, per quanto ora detto a proposito della 3.6, si ha:
²τ = ˆτ , ²p = ˆp − 1
Si osserva che in generale gli errori d’interpolazione dipendono dalla fase di campio-namento φ oltre che dalla durata dell’impulso, la lunghezza della finestra di osservazione, ecc.; nel seguito sar`a effettuata un’analisi di tali errori per alcune diverse tipologie di interpolatore, il che consentir`a in particolare di valutare il loro valore massimo, da con-frontare successivamente con gli errori introdotti dal rumore di osservazione.
3.3.1
Interpolazione parabolica
Questa tecnica d’interpolazione `e la pi´u semplice da implementare tra quelle considerate nel presente studio e consiste nell’imporre il passaggio di una curva parabolica attraverso tre campioni consecutivi. Essa si articola nei seguenti passi:
• ricerca del massimo assoluto della successione osservata, che in virt´u del modello 3.8 si trova sull’indice 0;
3.3. TECNICHE DI INTERPOLAZIONE 25
• fitting di una curva parabolica sul massimo suddetto e sui due campioni adiacenti;
• impiego della posizione temporale e del valore del massimo della parabola come stime ˆτ e ˆp della posizione e del valore di picco dell’impulso ricevuto.
Il fitting parabolico richiede la risoluzione di un sistema di tre equazioni lineari nelle tre incognite rappresentate dai coefficienti della parabola. Specificatamente, indicando con y−1, y0 e y1 la terna suddetta di campioni ed attribuendo fittiziamente ad essi, per
semplicit`a, le ascisse normalizzate −1, 0 e 1, si devono determinare i coefficienti a, b e c della parabola y = ax2+ bx + c che soddisfano le condizioni.
y−1 = a − b + c y0 = c (3.9) y1 = a + b + c Risolvendo, si trova: a = y1− 2y0+ y−1 2 b = y1− y−1 2 (3.10) c = y0
Il vertice della parabola si trova, come `e noto, in corrispondenza dell’ascissa norma-lizzata
xmax = −
b
a (3.11)
da cui denormalizzando l’ascissa, si trova:
ˆ
τ = φ + xmaxTc= φ −
bTc
2a (3.12)
mentre il valore di picco della parabola `e:
ˆ
p = ax2
max+ bxmax+ c
dalle 3.10-3.12 si vede che le stime trovate, e quindi anche gli errori di stima, dipendono ovviamente dal valore del parametro φ presente nella 3.8, sia in modo esplicito (dalla 3.12) sia implicitamente attraverso i coefficienti a, b e c.
Nel paragrafo 3.3.4 vengono presentati alcuni grafici degli errori ²τ e ²p in funzione
`e, tra i metodi considerati, quello pi´u facilmente implementabile, ma anche quello che conduce ad errori di stima maggiori, ed `e inoltre pi´u sensibile al rumore; esso si basa infatti sulla “somiglianza” del segnale di ingresso ad una parabola nell’intorno del picco (il che `e sempre possibile, ma sotto le condizioni note per lo sviluppo in serie di Taylor arrestato al termine quadratico), nonch´e sulla presenza di almeno tre campioni osservati entro tale intorno. In genere si trova che tale procedimento `e utilizzabile quando la frequenza di campionamento `e assai pi´u elevata della banda del segnale o, equivalentemente, quando all’interno della durata convenzionale d del picco cadono parecchi campioni. In caso contrario pu`o essere pi´u conveniente (anche se pi´u oneroso in termini di complessit`a di calcolo) ricorrere a tecniche polinomiali di ordine superiore al secondo o a metodi di interpolazione basati sull’uso di funzioni kernel, come descritto nei paragrafi successivi.
3.3.2
Interpolazione spline cubica
In questa sezione viene descritto l’algoritmo d’interpolazione tramite curve spline di terzo grado. Riformuliamo la successione 3.8 come segue:
yj = y(xj), j = 1, ..., N
dove xj rappresenta la successione degli istanti di campionamento xj = jTc + φ
sull’asse dei tempi x. Focalizzandoci su un intervallo [xj, xj+1] l’interpolazione lineare
in quell’intervallo `e data da:
y = Ayj+ Byj+1 (3.13) dove A ≡ xj+1− x xj+1− xj B ≡ x − xj+1 xj+1− xj = 1 − A
La curva espressa dalla 3.13 `e lineare a tratti, ha derivata seconda nulla all’interno del dominio di definizione e derivata seconda indefinita agli estremi. L’obiettivo di un algoritmo d’interpolazione tramite curve spline `e ottenere un’espressione continua e derivabile nella derivata prima e continua nella derivata seconda (in tutto l’intervallo e ai suoi estremi).
Supponiamo momentaneamente di avere a disposizione oltre ai campioni del segnale
yj anche la serie yj00 dei campioni della derivata seconda del segnale, calcolata esattamente
negli stessi punti xj.
Per ogni intervallo possiamo aggiungere al lato destro di 3.13 un polinomio di terzo grado, caratterizzato quindi da una derivata seconda che varia in maniera lineare da un estremo all’altro dell’intervallo. Imponendo la continuit`a tra un intervallo e l’altro (qui interviene la necessit`a di conoscere la serie delle derivate seconde) otteniamo la
3.3. TECNICHE DI INTERPOLAZIONE 27 derivata seconda continua e lineare. Inoltre se agli estremi di ogni intervallo imponiamo l’annullamento della funzione additiva allora in quei punti l’espressione risultante conti-nuer`a ad assumere i valori tabulati del segnale.
Con un p`o di algebra si pu`o dimostrare che la formula richiesta assume la seguente forma [5]:
y = Ayj + Byj+1+ Cyj00+ Dy00j+1 (3.14)
dove A e B sono stati definiti in 3.13 mentre
C ≡ 1 6(A 3− A)(x j+1− xj)2 D ≡ 1 6(B 3− B)(x j+1− xj)2
Possiamo verificare che la derivata seconda di y coincide effettivamente con i valori che abbiamo ipotizzato di conoscere. Derivando infatti rispetto a x:
d y d x = yj+1− yj xj+1− xj − 3A 2− 1 6 (xj+1− xj)y 00 j + 3B2− 1 6 (xj+1− xj)y 00 j+1 (3.15)
e ripetendo la stessa operazione: d2y
d x2 = Ay
00
j + By00j+1.
Tenendo conto del fatto che A = 1 per x = xj e A = 0 per x = xj+1 mentre per B
vale il viceversa, la dimostrazione `e completata.
A questo punto dobbiamo ricordare che per realizzare effettivamente il procedimento fin qui descritto `e necessario conoscere la serie delle derivate seconde. Ricordiamo a tale proposito l’espressione per la derivata prima calcolata precedentemente (equazione 3.15); sfruttiamo quindi un requisito fondamentale dell’interpolazione spline fino ad ora rimasto inutilizzato, ovvero la continuit`a della derivata prima tra un intervallo e il suo adiacente. Otteniamo dunque un insieme di 2N − 1 equazioni (ovvero pari al numero dei campioni osservati diminuito di 2), dove le derivate seconde compaiono come incognite; dopo qualche semplificazione ecco come appare la generica equazione per il j-esimo intervallo:
xj − xj−1 6 y 00 j−1+ xj+1− xj−1 3 y 00 j + xj+1− xj 6 y 00 j+1 = yj+1− yj xj+1− xj − yj − yj−1 xj − xj−1 (3.16)
Per ottenere una soluzione unica per il sistema 3.16 `e necessario specificare due condizioni ulteriori tipicamente definite da vincoli sugli estremi x−N e xN. Possibili
convenzioni al riguardo sono:
• Imporre una o entrambe le y00
−N e yN00 uguali a zero. Si ottiene la cosiddetta spline
−N N
l’equazione 3.15; per fare questo `e necessario specificare i valori delle derivate prime agli estremi (y0
−N e yN0 ).
L’implementazione di un algoritmo risolutivo del sistema 3.16 `e particolarmente fa-vorita dal punto di vista della complessit`a in quanto essendo un sistema tridiagonale (in cui ogni incognita `e accoppiata al pi´u con l’elemento immediatamente successivo o immediatamente precedente) `e possibile ottenere la soluzione in O(N) operazioni.
Quando la tecnica di interpolazione descritta `e applicata alla successione 3.8 di campio-ni di un impulso gaussiano, si ottengono degli errori di stima della posizione e dell’ampiezza del picco di regola inferiori rispetto a quelli manifestati dall’interpolatore parabolico descritto al paragrafo 3.3.1. Le curve degli errori ²τ e ²p in funzione di φ sono presentate
nel paragrafo 3.3.4 per alcuni valori tipici dei parametri caratterizzanti il sistema.
Il calcolo del massimo pu`o essere effettuato andando a cercare gli zeri della funzione spline interpolante nell’intervallo tra due campioni che contiene il massimo della funzione sottostante 3.6. Tale intervallo, stanti le assunzioni stabilite all’inizio di questa sezione, risulta essere (x−1, x0) o (x0, x−1) rispettivamente a seconda che y−1sia maggiore o minore
di y1. La risoluzione del sistema 3.10 fornisce in particolare i coefficienti a0, b0, c0 e d0 del
polinomio interpolatore di terzo grado che copre l’intervallo suddetto:
y = a0x3+ b0x2+ c0x + d0 (3.17)
Si vanno quindi a ricercare gli zeri della derivata di 3.17 risolvendo l’equazione di secondo grado:
d y d x = 3a
0x2+ 2b0x + c0 = 0
la quale, quando la frequenza di campionamento `e sufficientemente elevata, fornisce una sola soluzione entro l’intervallo sopra menzionato, essendo l’altra soluzione tipicamente molto lontana.
Per concludere, si fa osservare che la complessit`a della tecnica di interpolazione a spline cubica pu`o essere notevolmente ridotta se ci si limita a calcolare i coefficienti dei polinomi interpolatori solo per una limitata finestra di campioni osservati centrata sul loro massimo; l’effetto dei campioni periferici sui polinomi interpolatori relativi agli intervalli centrali `e infatti trascurabile gi`a a partire da pochi campioni.
3.3.3
Interpolazione con funzioni kernel a banda limitata
Lo schema d’interpolazione descritto in questa sezione discende dalle tecniche di ricostru-zione di un segnale tempo-continuo a partire dai suoi campioni, quando la spaziatura di questi ultimi soddisfi le condizioni del teorema del campionamento.
3.3. TECNICHE DI INTERPOLAZIONE 29 Supponiamo dunque di avere campionato un segnale analogico xa(t) avente trasformata
di Fourier (o spettro) Xa(iΩ), dove Ω = 2πf `e la frequenza angolare o pulsazione (rad/s)
e f `e la frequenza (Hz), con periodo di campionamento Tc, e di avere cos`ı prodotto una
serie tempo-discreta xn = xa(nTc). Si ammetta inoltre che Xa(iΩ) abbia limite superiore
di banda finito pari a B (Hz), vale a dire |Xa(iΩ) = 0| per |Ω| > 2πB. La trasformata di
Fourier (o spettro) della successione xn `e definita come:
X[exp (iΩTc)] = ∞
X
n=−∞
xnexp(−inΩTc) (3.18)
Si pu`o dimostrare che lo spettro 3.18 `e proporzionale alla serie infinita di repliche dello spettro di xa(t) traslate una rispetto all’altra della frequenza di campionamento, come
segue: X[exp (iΩTc)] = 1 Tc ∞ X r=−∞ Xa(iΩ + i2πr/Tc) (3.19)
Si `e gi`a sottolineato come un campionamento effettuato a velocit`a sufficientemente elevata eviti la sovrapposizione tra le diverse copie spettrali, essendo queste limitate in banda; come `e facile rilevare dalla 3.19, ci`o avviene solamente se la frequenza di campionamento ha valore non inferiore al doppio della banda del segnale: fc= 1/Tc≥ 2B.
Sotto questa ipotesi, `e possibile risalire al valore esatto di xa(t) per ogni istante t a
partire dai campioni xn (`e il ben noto teorema del campionamento): infatti nell’intervallo
−π/Tc ≤ Ω ≤ π/Tc, che contiene l’intera banda (−2πB, 2πB) di xa(t), lo spettro
X[exp (iΩTc)] coincide, a meno di un irrilevante fattore moltiplicativo, con Xa(iΩ).
Vediamo adesso come sia possibile recuperare (almeno matematicamente) il valore di xa(t) dalla successione xn: si inizia con l’osservare che xa(t) si pu`o ottenere come
antitrasformata di Fourier di Xa(iΩ):
xa(t) = 1
2π Z ∞
−∞
Xa(iΩ) exp (iΩt) d Ω = 1
2π Z 2πB
−2πB
Xa(iΩ) exp (iΩt) d Ω (3.20)
Sotto l’ipotesi di validit`a del teorema del campionamento e ricordando la 3.19, conviene scrivere la 3.20 nel seguente modo:
xa(t) =
Tc
2π
Z 2π(1/Tc−B)
−2π(1/Tc−B)
X[exp (iΩTc)]H(iΩ) exp (iΩt) d Ω (3.21)
dove si `e introdotta la funzione H(iΩ) con la condizione che essa assuma valore unitario nella banda del segnale xa(t) e andamento arbitrario nel resto dell’intervallo
H(iΩ) =
(
1, |Ω| ≤ 2πB
qualunque andamento, 2πB ≤ |Ω| ≤ 2π(1/Tc− B)
(3.22)
Sostituendo la 3.18 nella 3.21 si arriva a:
xa(t) = ∞ X n=−∞ xn 1 2π Z 2π(1/Tc−B) −2π(1/Tc−B)
TcH(iΩ) exp [iΩ(t − inTc)] d Ω (3.23)
ovvero, indicando con g(t) l’antitrasformata di Fourier di TcH(iΩ) ristretta all’intervallo
−2π(1/Tc− B) ≤ Ω ≤ 2π(1/Tc− B):
g(t) = 1
2π
Z 2π(1/Tc−B)
−2π(1/Tc−B)
TcH(iΩ) exp (iΩt) d Ω (3.24)
la 3.23 diviene: xa(t) = ∞ X n=−∞ xng(t − nTc). (3.25)
Come si vede, questa espressione consente di recuperare il segnale xa(t) a partire dai
campioni xn; la funzione g(t), che consente di interpolare tra un campione e l’altro, si dice
anche kernel di interpolazione. Come si vede, la funzione kernel, essendo rigorosamente limitata in banda (come discende dalla 3.24), presenta lunghezza infinita nel dominio del tempo, e ci`o implica che la sommatoria in 3.25 sia costituita da un numero infinito di termini. In pratica sar`a necessario troncare la sommatoria suddetta ad un numero finito di termini, e ci`o pone un problema di scelta congiunta ottimale sia del kernel che del numero di termini. Come si intuisce facilmente, infatti, esistono delle funzioni kernel che assicurano una convergenza pi´u veloce della serie 3.25 e che quindi conviene utilizzare a parit`a del numero dei termini allo scopo di minimizzare gli errori di interpolazione.
Un kernel matematicamente semplice, ma caratterizzato da una convergenza molto lenta della serie 3.25, `e quello che si ottiene imponendo che la funzione H(iΩ) assuma valore unitario entro l’intervallo −π/Tc ≤ Ω ≤ π/Tc, e nullo altrove; in tal caso dalla 3.24
si trova subito il cosiddetto interpolatore “cardinale”:
g(t) = sinc µ t Tc ¶ (3.26)
dove si `e definito sinc(x) = sin(πx)/(πx). La 3.26, sostituita nella 3.25, conduce a:
xa(t) = ∞ X n=−∞ xa(nTc) · sinc µ t − nTc Tc ¶ .