Sincronizzazione di circuiti caotici di Chua: analisi di robustezza

Università degli studi di Napoli Federico II 

Facoltà di Ingegneria 

Corso di Laurea Specialistica in 

Ingegneria Elettronica 

(Classe delle Lauree in Ingegneria dell’Informazione) 

Dipartimento di Ingegneria Elettrica 

Tesi di Laurea 

Sincronizzazione di Circuiti Caotici di Chua: 

Analisi di Robustezza

Relatori

Ch.mo Prof. 

Massimiliano de  Magistris 

Ch.mo Prof.  

Mario Di Bernardo 

Candidata

Paola Della Corte

Matr. 884/162

Anno Accademico 2008‐2009 

Indice 

3.3  Sincronizzazione delle Dinamiche di Circuiti Caotici ______________  46  3.4 Esempi d’Interesse in Letteratura _________________________________  51  3.5  Particolarizzazione del Modello di Accoppiamento per i Casi di  Studio _________________________________________________________  56  3.6 Cenno sui Sistemi Ipercaotici ____________________________________  59  3 Capitolo 4  ___________________________________________________ 60  4 Realizzazione, Simulazioni e Verifiche Sperimentali _____________ 60  4.1 Definizione del Lay‐out  ________________________________________  60  4.1.1 L’induttore ________________________________________________  62  4.1.2 Il diodo di Chua ___________________________________________  63  4.1.3 Componenti e tolleranze ____________________________________  68  4.2  Simulazione e Realizzazione Hardware della Topologia Scelta  _____  69  4.3  Simulazioni SPICE della Sincronizzazione ________________________  75  4.3.1 Coppia di circuiti __________________________________________  76  4.3.2 Tris di circuiti  _____________________________________________  80  4.3.3 Considerazioni sulle simulazioni ____________________________  91  4.4 Risultati Sperimentali ___________________________________________  92  4.4.1 Coppia di circuiti __________________________________________  94  4.4.2 Tris di circuiti  ____________________________________________  104  4.4.3  Analisi dei Risultati  ______________________________________  124  4.5 Conclusioni ___________________________________________________  127   Riferimenti Bibliografici ______________________________________ 129      

Introduzione 

Negli  ultimi  decenni  un  interesse  sempre  crescente  della  comunità  scientifica  per  le  dinamiche  dei  sistemi  non  lineari  ha  portato  allo  sviluppo  della  teoria  del  Caos  Deterministico,  la  quale  pone  limiti  definiti alla prevedibilità dell’evoluzione dei sistemi complessi. Questa  imprevedibilità,  strettamente  legata  ad  un  fattore  di  incertezza  sulle  condizioni iniziali del sistema, si pone alla base di un “nuovo mondo”  costituito  dalle  dinamiche  caotiche  del  sistema  stesso,  e  che  permette  numerosi esempi nella vita quotidiana: basti pensare al cuore umano. E’  stato sperimentalmente provato che l’andamento del battito cardiaco di  una  persona  sana  è  intrinsecamente  caotico,  ed  anzi  la  periodicità  è  sintomo  di  disfunzioni  e  patologie.  Ancora,  numerosi  sistemi  biologici  complessi,  come  quelli  cellulari,  mostrano  una  intrinseca  capacità  di  sincronizzazione. La sincronizzazione di sistemi caotici complessi, oltre  alla  sua  massiccia  presenza  in  natura,  trova  spazio  nel  mondo  “artificiale”,  quale  quello  delle  tecnologie.  Tra  le  diverse  applicazioni,  ricordiamo quella che permette di realizzare, mediante la definizione di  un apposito schema crittografico, un canale di comunicazione sicuro da  intrusioni  esterne.  Ciò  può  essere  ottenuto  proprio  a  partire  dalla  possibilità  sincronizzare  fra  loro  due  o  più  sistemi  di  tipo  caotico,  per  mascherare il messaggio e garantirne la non intellegibilità a terzi. 

Per  poter  studiare  le  dinamiche  di  sincronizzazione  è  necessario  anzitutto  disporre  di  un  sistema  caotico,  dotato  cioè  di  alta 

impredicibilità  dell’uscita  in  funzione  dei  parametri  di  ingresso.  Dal  punto  di  vista  circuitale  la  via  migliore  sotto  molti  punti  di  vista  prevede l’utilizzo del circuito di Chua. Esso costituisce il più semplice  esempio  di  circuito  caotico  ed  inoltre  è  economicamente  accessibile  e  semplice da realizzare.  

Obiettivo  della  tesi  è  lo  studio  preliminare,  numerico  e  sperimentale,  delle  dinamiche  di  sincronizzazione  di  più  circuiti  di  Chua,  al  fine  di  analizzare le condizioni che ne garantiscano la robustezza (qualora esse  esistano).   

L’analisi  è  stata  effettuata  attraverso  due  fasi  temporali,  una  prima  di  studio  teorico  dell’argomento  e  della  letteratura  d’interesse,  ed  una  successiva  che  consiste  nelle  verifiche  sperimentali.  Tale  suddivisione  dell’operato  è  altresì  riscontrabile  nel  presente  elaborato,  che  consta  quindi di due parti.  

La prima parte, costituita da tre capitoli, affronta lo studio della teoria  del  caos,  con  richiami  a  concetti  chiave  della  dinamica  dei  sistemi,  nonché  presenta  spunti  applicativi  della  stessa.  Successivamente  si  analizza  in  dettaglio  la  topologia  e  le  dinamiche  del  circuito  di  Chua,  “protagonista” del lavoro. Infine, nel terzo capitolo, vengono introdotti  i  concetti  di  sincronizzazione,  e  sincronizzazione  di  reti  di  sistemi  caotici,  con  una  particolare  attenzione  alla  sincronizzazione  di  circuiti  caotici di Chua tramite lo studio di esempi presenti in letteratura. 

La  seconda  parte  dell’elaborato  è  di  carattere  implementativo:  in  essa  vengono  presentati  il  modello  matematico  linearizzato  che  descrive  il  problema  in  esame,    la  soluzione  topologica  adottata  per  la  realizzazione  dei  circuiti,  e  i  risultati  delle  analisi  effettuate  al  calcolatore  delle  dinamiche  degli  stessi  nonché  dei  tentativi  di  sincronizzazione,  effettuati  mediante  l’ausilio  dei  software  SwCad  e  MatLab.  Infine,  alla  verifica  al  calcolatore  si  aggiunge  la  prova  sperimentale  vera  e  propria:  i  circuiti  di  Chua  sono  stati  realizzati  presso  il  Laboratorio  di  Elettrotecnica  del  Dipartimento  di  Ingegneria  Elettrica  dell’Università  Federico  II,  ed  è  stato  verificato  il  loro 

funzionamento  e  la  capacità  di  sincronizzazione.  L’elaborazione  dei  dati sperimentali è avvenuta  con il supporto del software LabView.   Nel corso del lavoro sono stati analizzati diversi possibili scenari, per i  quali  sono  state  identificate  le  condizioni  parametriche  necessarie  a  garantire  sincronia  al  sistema  complessivo.  Ciò  si  pone  come  fondamento  per  successivi  studi  di  robustezza  della  sincronizzazione  per reti complesse di circuiti caotici. 

C

APITOLO 

1

I

L 

C

AOS 

D

ETERMINISTICO

1.1

I

Risultati  recenti  dellʹevoluzione  della  fisica  degli  ultimi  venti  anni  hanno  ultimato  probabilmente  in  modo  definitivo  quel  lavoro  di  distruzione della visione Laplaciana della realtà fisica come ʺuniverso‐ orologioʺ  e  del  mondo  come    retto  da  perfette  e  perfettamente  conoscibili  leggi  dʹevoluzione,  iniziato  alla  fine  del  secolo  scorso.  Se  la 

meccanica  quantistica  introduceva  il  caso  in  un  modo  per  così  dire 

esterno  e  a  priori,  lʹevoluzione  della  teoria  dei  sistemi  dinamici  lo 

scopriva  a  posteriori  dentro  teorie,  là  dove  era  sempre  stato,  passando  inosservato  o  quasi.  Naturalmente  il  caso  quantistico  e  quello 

deterministico dei sistemi caotici sono due ʺcasiʺ diversi. Il primo è posto 

come un attributo della realtà fisica in sé, il secondo continua ad essere  frutto, classicamente, della finitezza dei nostri mezzi. Ma ciò che risulta  oltremodo  significativo  è  che  le  conseguenze  di  questa  finitezza  sono  assai di più vasta portata di quanto si potesse a prima vista sospettare:  essa  finisce  per  impedire  in  linea  di  principio  previsioni  affidabili  sul  comportamento della realtà fisica, anche la più banale, o meglio confina  queste  previsioni  entro  un  orizzonte  temporale  ristretto,  spesso  sorprendentemente  ristretto.  Il  Caos,  in  questo  significato  artificiale  della  teoria  delle  reti  elettriche  e  della  teoria  dei  sistemi,  è  appunto  lʹesistenza  di  un  orizzonte  finito  di  predicibilità  dei  sistemi,  effetto  di  una  sensibilità  alle  condizioni  iniziali  che  amplifica  lʹindeterminazione  iniziale,  per  quanto  piccola  essa  sia,  sulla  conoscenza  del  sistema.  I  sistemi  non  sono  dunque  buoni:  non  conservano,  ma  amplificano,  gli  errori. 

Come  per  il  caos,  anche  la  complessità  ci  si  presenta  oggi  come  un  concetto emergente e denso di significato. ʺComplessoʺ indica qualcosa  di molto articolato, di composto di molte parti interagenti tra loro, certo  in maniera non banale, in modo cioè che le parti abbiano tutte un certo  grado  di  autonomia  l’una  dall’altra,  ma  siano  anche  dipendenti  lʹuna  dallʹaltra. C’è un nesso tra complessità e caos? Il caos è forse nientʹaltro  che il frutto della complessità? 

La risposta, come sappiamo, è no. Sono caotici anche sistemi piuttosto  semplici,  anche  molto  semplici,  come  un  pendolo,  ad  esempio.  Viceversa,  non  è  detto  che  un  sistema  complesso  mostri  necessariamente  un  comportamento  caotico.  Quello  che  però  avviene  sicuramente  in  un  sistema  caotico  è  che  se  si  esplora  lo  spazio  delle  possibili  evoluzioni  a  partire  da  un  insieme  ristretto  e  ʺsempliceʺ  di  possibilità iniziali, si ottiene qualcosa di molto complesso, cioè di dotato 

di  molti  dettagli  e  popolato  di  molte  parti  e  alternative.  Eʹ  da  lì  che  nasce  appunto,  lʹimpossibilità  di  una  previsione.  Lʹuniverso  delle  possibili evoluzioni diventa sempre più complesso, man  mano che ci si  spinge in là con il tempo. 

1.2

G

S

D

1.2.1 Nozioni di base 

 Cominciamo  col  definire  un  sistema  dinamico  dal  punto  di  vista  analitico:  un  sistema  dinamico  è  un  sistema  di  equazioni  differenziali  della forma: 

( , )

x_  f x t  

Con f U: Rn, e con  U aperto su Rn _×R e   x dx

dt

  . 

Lo  spazio  delle  variabili  dipendenti  è  il  cosiddetto  spazio  delle  fasi  o 

degli stati.  

Per soluzione  del sistema dinamico si intende una mappa  φ : U → Rn _, con 

I    intervallo  su  R.  Si  può  interpretare  φ  come  una  curva  nello  spazio  delle fasi,  con f  campo di vettori tangenti alla curva.  

È  necessario  ricordare  il  classico  risultato  del  teorema  di  esistenza  e  unicità: 

supponendo che f sia di classe Cr  _{su di U, ( f   C}r _{(U) ) e che per t1, t2} 

siano I1 = {t   R : t0 − t1 < t< t0 + t1} e I2 = {t   R : t0 − t2 < t <t0 + t2}, allora 

vale il seguente: 

Teorema (di esistenza e unicità) 

Sia (x0,t0)   U, allora per un t1 sufficientemente piccolo esiste una soluzione φ1 

del sistema dinamico tale che φ1 : I1 → Rn,φ1(t0)= x0.  

Se f   Cr_{(U), r ≥ 1, ed esiste φ2 : I2 → R}n_{, φ2(t0)= x0, allora φ1 = φ2,  t   I3, con} 

I3 = {t   R : t0 − t3 < t < t0 + t3} e t3 = min(t1,t2). 

Osservazione  

Si  utilizza  qui  una  versione  del  teorema  di  esistenza  e  unicità  con  ipotesi più forti su f, dato che la natura di f non è mai un problema nelle  applicazioni che tratteremo.  

Altro importante risultato nelle applicazioni è il seguente: 

Teorema  

Se f   Cr _{(U) allora la soluzione φ(t, t0, x0) è di classe C}r _{per le variabili t, t0, x0.}  

Osservazione  

 Questo  permette  di  fare  lo  sviluppo  di  Taylor  di  una  soluzione  nellʹintorno di una data condizione iniziale.  

Definizione  

Sia  I  un  intervallo  aperto  e  A  una  funzione  A  :  I  →  Mn×n e  siano  le  funzioni u1,...,un una base di soluzioni del sistema lineare omogeneo: 

v Av

_









Nel  caso  in  cui  i  coefficienti  A  siano  costanti,  la  matrice Z 





viene detta matrice risolvente quando Z(0) = Id.  

Osservazione  

 Se  i  coefficienti  sono  costanti,  posta  R  =  Z(t)Z−1(0),  la  soluzione  al 

problema omogeneo è: 

u(t)= R(t − t0). 

Il  teorema  di  esistenza  ed  unicità  garantisce  la  soluzione  solo  per  un  piccolo intervallo. Per enunciare il teorema che consente di estendere la  soluzione, è necessaria la seguente:  

Definizione  

Sia  φ1  una  soluzione  del  sistema  dinamico  definita  su  I1  e  φ2  una 

soluzione  del  medesimo  sistema  definita  su  I2.  Si  definisce  φ2  un 

prolungamento di φ1 se I1   I2 e φ2 = φ2 su I1. Una soluzione è detta non 

prolungabile  se  il  suo  prolungamento  non  esiste,  ed  in  tal  caso  viene  definito l’intervallo massimo di esistenza.  

Teorema  

Sia  f    Cr(U)  e  φ  una  soluzione  del  sistema  dinamico,  allora  esiste  un  prolungamento  di  φ  fino  ad  un  intervallo  di  massima  esistenza.  Inoltre,  se  (t1,t2) è un intervallo massimo di esistenza, allora (φ(t),t) tende al bordo di U 

per t → t1, t → t2.  

1.2.2 Sistemi autonomi e non autonomi  

I  sistemi  dinamici  possono  essere  caratterizzati  dal  fatto  che  il  campo  vettoriale  dipenda  in  maniera  esplicita  o  meno  dal  parametro  indipendente t (tempo).  

Sistemi autonomi 

Un  sistema  autonomo  di  equazioni  differenziali  ordinarie  è  caratterizzato dallʹespressione : 

xֹ= f (x) 

con  f  :  U  →  Rn con  U  aperto  su  Rn e  φ  una  soluzione  del  sistema.  Si  verifica  facilmente  che  la  soluzione  di  un  sistema  autonomo  è  indipendente  da  un  incremento  del  parametro  indipendente,  cioè  se 

φ(t)  è  una  soluzione,  allora  lo  è  anche  φ(t  +  τ  )  τ    R.  Seguono  due 

importanti proprietà dei sistemi autonomi.    

Proprietà 1 

Sia  f    Cr(U),  r  ≥  1,  φ1  una  soluzione  del  sistema  dinamico  autonomo 

definita  su  I1  e  φ1  una  soluzione  del  medesimo  sistema  definita  su  I2 , 

Proprietà 2 

Sia  f    Cr(U),  r  ≥  1,  φ  una  soluzione  del  sistema  dinamico  autonomo 

definita su I. Supponiamo esistere due valori t1,t2   I tali che φ(t1)= φ(t2), 

allora la soluzione φ(t) esiste  t   R ed è periodica in t di periodo T = t2 

− t1, ovvero φ(t)= φ(t + T ) t   R.  

Queste due proprietà dicono che due soluzioni qualsiasi (e quindi tutte  le  orbite)  non  possono  coincidere  su  di  uno  stesso  punto  senza  coincidere nel loro intervallo di definizione.  

Sistemi non autonomi 

Un sistema si dice non autonomo se il suo campo di vettori dipende in  maniera  esplicita  dalla  variabile  indipendente  tempo.  Quindi  la  sua  espressione è:  

xֹ= f (x, t) 

con  f  :  U  →  Rn,  con  U  aperto  su  Rn ×  R  e  φ  soluzione  del  sistema  non 

autonomo.     Le proprietà espresse per i sistemi autonomi non valgono per quelli non  autonomi, ma è sempre possibile scrivere un sistema non autonomo in  forma di sistema autonomo.   Per la regola della catena:   ( , ) 1 dx dx ds f x t dt  ds dt      È allora possibile scrivere il  sistema nel nuovo parametro indipendente  s: 

' ( , ) ' 1 dx x f x t dt dt t ds        

Si  definisce  il  nuovo  vettore  delle  variabili  di  stato  y  =[x,  t],  quindi  il  sistema non autonomo diviene: 

' ( ) [ ( ),1]

y  g y  f y    

che  risulta  autonomo  nella  variabile  s.    Infatti  ad  una  soluzione  φ  del  sistema non autonomo che passa per (x0,t0),  corrisponde una soluzione 

ϕ(s) del sistema autonomo dallʹespressione ϕ(s)=[φ(s+t0), t(s)= s+t0], con 

s0 =0.  

Questo  banale  accorgimento  consente  di  tenere  conto  solo  dei  sistemi  autonomi nei risultati che seguiranno.  

1.2.3 Stabilità delle soluzioni 

La nozione di stabilità (o di instabilità) è molto importante nello studio  di  una  soluzione,  infatti  la  stabilità  garantisce  in  qualche  modo  una  proporzionalità  tra  la  perturbazione  dellʹingresso  di  un  sistema  dinamico  e  la  sua  perturbazione.  In  linea  di  principio  una  soluzione  stabile di un sistema dinamico se leggermente perturbato varia di poco  la sua evoluzione.  

Si  definisce  in  maniera  analitica  questa  forte  proprietà  con  la  definizione dovuta a Lyapunov:  

Sia  φ(t,  0,  x0)  una  soluzione  del  sistema  dinamico  autonomo  definita 

nellʹintervallo  massimale  destro  I+,  che  si  può  sempre  supporre  come   [0, +∞)  

Definizione (stabilità secondo Lyapunov) 

La soluzione φ(t, 0, x0) si dice stabile (secondo Lyapunov) se  t > 0,   δ = 

δ(t) tale che: 

se  x0 x0  allora la soluzione 





Se inoltre ||ψ(t) − φ(t)|| → 0 per t →∞, φ si dice asintoticamente stabile.  

In pratica per una soluzione stabile secondo Lyapunov, se si da origine  ad  un  orbita  sufficientemente  vicino  al  x0,  essa  rimarrà  confinata  nelle 

vicinanze di φ(t). Unʹorbita che non è stabile è detta instabile.  

Metodo di linearizzazione 

Il  metodo  di  linearizzazione  consente  di  determinare  la  stabilità  locale  di un sistema dinamico nellʹintorno di una data soluzione.  

Si consideri il sistema autonomo  

y  = f (y, t) 

con f   C1 _{(Ω), Ω aperto su R}n _{e tale che f(0) = 0 e sia Df(0) non singolare.}  

Sviluppiamo nellʹorigine la nostra f, che ricordiamo essere (almeno) C1_:  ( ) (0) ( ). f y Df y o y   Si ponga A ≡ Dyf(0) e si consideri il sistema (sistema linearizzato) : 

z Az

_



Teorema  

Se  lʹorigine  è  asintoticamente  stabile  per  il  sistema 

z Az





c) se la soluzione per è asintoticamente stabile t

x o x t a t x b A t z Az           Risulta ovvio ricondursi al teorema precedente trasformando il sistema  non autonomo in un sistema autonomo.    

1.2.4 Mappe di Poincaré 

La  mappa  di  Poincaré  è  una  tecnica  che  consente  di  trasformare  un  sistema di equazioni differenziali in un sistema discreto, comportando  una  serie  di  vantaggi,  tra  i  quali  la  riduzione  delle  dimensioni  del  problema, senza nulla perdere in termini di interpretabilità dei risultati  ottenuti. Lʹidea di fondo di questa tecnica è, dato un sistema dinamico  autonomo,  prendere  una  varietà  Σ,  n  −  1‐dimensionale,  nello  spazio  delle  fasi,  tale  che  sia  trasversale  al  campo  dei  vettori  nel  punto 

x

( ) ( ) 0

n x f x      

Supponiamo di avere una soluzione γ di periodo T per il nostro sistema  dinamico.  Allora  si  posizioni  Σ  su  di  un  punto  di  questa  orbita.  Eʹ  possibile  trovare  su  Σ  un  sottoinsieme  aperto  V  ,  tale  che  x    V  ,  il  tempo che impiega un orbita originata da x a ritornare in Σ è prossimo  al periodo T . Chiamiamo questo tempo di ritorno con τ : V → R.   Allora si definisce la mappa di Poincaré P come la mappa che relaziona  un punto su V con il punto in cui lʹorbita da esso generata incide su Σ la  prima volta. Quindi:   : ( ( ), ) P V x   x x       

Eʹ  legittimo  chiedersi  come,  data  lʹarbitrarietà  delle  superfici  di  Poincaré,  le  mappe  varino  al  variare  delle  superfici.  Eʹ  possibile  dimostrare che, prese due superfici Σ1, Σ2 e di conseguenza due mappe 

P1 e P2, esse siano localmente coniugate,   cioè una funzione h tale che:  

P1 ◦ h = h ◦ P2 

Con h un difeomorfismo di classe Cr (mappa di classe Cr con una inversa  anchʹessa di classe Cr) , tale che:  

h(Σ1)=Σ2 

È  possibile  estendere  questa  idea  ad  un  sistema  dinamico  autonomo,  effettuando  una  cosiddetta  mappatura  stroboscopia.  Tale  tecnica  consiste  nel  prendere  un  orbita  φ(t,  x0)  e  posizionare  delle  superfici 

trasversali  alla  traiettoria  scelta  con  periodo  T  .  Quindi  creare  una  mappa:   1 : ( ( ), ) k k P x   x x         

Questa  mappatura  ci  servirà  per  poter  trovare  agevolmente  gli  esponenti di Lyapunov per un sistema continuo.  

1.2.5 Esponenti di Lyapunov 

Ora per trattare questo fondamentale argomento nellʹambito dei sistemi  dinamici  utilizzerà  un  approccio  intuitivo,  cercando  di  generalizzare  a  partire dal semplice caso di una equazione di ricorrenza.   Si consideri, allʹinizio, unʹequazione di ricorrenza:   1 ( ) k k x_  f x   E si prenda una sua traiettoria, originata da x0:  





e  la  traiettoria  originata  da  x0  sottoposto  ad  una  perturbazione,  che 

chiameremox₀:  





Per  poter  apprezzare  di  quanto  varia  la  dinamica  del  sistema  sotto  lʹeffetto  della  perturbazione,  si  vuole  valutare  il  valore  e1   x1 x1  

attraverso uno sviluppo lineare. Assumendo che e0 sia piccolo   1 1 1 ( )0 ( )0 '( )0 0 ( )0 e   x x_ f x  f x_  f x e o e .  Dopo t istanti si ha che:  0 1 ' 0 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) t ( ) ( ) t t t t k k x d e f x f x f x e o e f x e o e dx      _{ }   _{  }  _{ }    



1 1 ' ' 0 0 0 0 ( ) exp ln ( ) . t t t t t t k k k k e  f x e t  f x e         _ _   _ _   





dove x0 è l’esponente di Lyapunov relativo all’orbita generata da x0 e la 

sua definizione è:  1 ' 0 1 ( ) lim ln_o t ( )_k t k L x f x t   _    _{ } 



si  allontana  indefinitamente,  se  L(x0)=0  la  distanza  rimane  costante, 

mentre  per  L(x0)  >  0  la  perturbazione  si  esaurisce  riportando  lʹorbita 

perturbata su quella originale. Per un sistema monodimensionale, se la  sua  orbita  è  non  periodica,    il  valore  dellʹesponente  non  può  essere  calcolato  esattamente,  ma  viene  iterata  la  sua  definizione  finché  non  converge.  

Tale concetto può essere generalizzato per un sistema, sempre discreto,  ma di dimensione n.  

Si supponga di avere un sfera n‐dimensionale di raggio infinitesimo con  condizioni  iniziali  nello  spazio  delle  fasi.  Se  si  trasforma  la  sfera  sotto  lʹazione  di  una  trasformazione  lineare,  la  sfera  diviene  un  ellisse,  i  cui  semiassi,  diretti  lungo  le  direzioni  principali,  sono  lunghi  (considerando  il  raggio  della  sfera  di  partenza  unitario)  al  tempo  t, 

1( ) 2( ) ... n( ) r t r t  r t    A partire da questi valori, si definiscono gli esponenti di Lyapunov per  la direzione i‐esima:  1 ( ) lim lnt ( ) lim ln ( ) i o _t i _t i L x r t r t t      

Quindi  per  come  abbiamo  ordinato  le  lunghezze  e  per  come  abbiamo  definito gli esponenti:  

1( ) 2( ) ... n( )

L t L t  L t  

Alternativamente  gli  esponenti  di  Lyapunov  possono  essere  calcolati  con la seguente definizione:  1 1 0 0 0 1 ( ) lim ln ( ) ( ) T t t i _t i k k k k L x D x D x t     _{ } _{   }     _{    }       





Indicando  con  λi{•}  lʹautovalore  i‐esimo  della  matrice  in  argomento,  e 

definendo:  1 1 0 0 ( ) ( ) T t t k k k k M  D x  D x            





Anche  qui  lʹesponente  di  Lyapunov  esprime  il  tasso  medio  al  quale  la  distanza  di  un  orbita  converge  o  diverge,  diretta  lungo  la  direzione  indicata  dallʹautovettore  corrispondente.  Come  detto,  la  matrice  M  è  simmetrica  e  quindi  grazie  al  teorema  spettrale  i  suoi  autovalori  sono  reali e gli autovettori formano una base ortonormale dellʹautospazio. Si  può quindi dire che lʹesponente di Lyapunov L1(x0) indica la direzione 

di maggior crescita, mentre in generale lʹi‐esimo esponente Li(x0) indica 

la direzione di maggiore crescita tra quelle ortogonali alle direzioni che  lo  precedono  nellʹordinamento  indicato  (quindi,  ad  esempio,  il  terzo  esponente  è  la  direzione  di  maggiore  crescita  nello  spazio  ortogonale  alla  prima  e  alla  seconda  direzione,  e  così  via).  Lungo  una  generica  direzione  e0  (  che  può  essere  vista  come  combinazione  degli 

autovettori considerati ) anche la divergenza dellʹorbita può essere vista  come  combinazione  dei  moti  proiettati  lungo  gli  autovettori.  Per  una  quantità  di  tempo  sufficientemente  elevata  i  moti  relativi  agli  altri  esponenti  diventeranno  trascurabili  rispetto  a  quello  relativo  a  L1(x0). 

Allora per t→∞:   1( )0 0 L x t t e e e . 

Lʹesponente maggiore quindi, a lungo andare, caratterizza la dinamica  del sistema.  

Sistemi tempo‐continui 

Per  un  sistema  a  tempo  continuo  lʹidea  di  esponente  di  Lyapunov  rimane sostanzialmente la stessa, cioè il tasso medio di divergenza delle  orbite perturbate. Per un sistema a tempo continuo è possibile definire  una  mappa  stroboscopica  di  periodo  T  che  associa  al  punto  x  la  sua  posizione a dopo T istanti:  

x((k + 1)T )= P (x(kT ))  T > 0 

e  poi  calcolare  gli  esponenti  di  Lyapunov  L xi( )o     per  la  mappa 

stroboscopica.  Gli  esponenti  di  Lyapunov  del  sistema  continuo  originale possono essere trovati sapendo che:  ( ) ( ) i o i o L x L x T   .      Osservazione  

Benchè  la  scelta  di  T  sia  arbitraria,  è  sempre  conveniente  prende  T  piccolo,  perché  una  scelta  di  T  grande  indurrebbe  molti  errori  nelle  simulazioni  numeriche.  Infatti  le  definizioni  degli  esponenti  di  Lyapunov nel caso n> 1 sono numericamente divergenti.  

Esistono  comunque  molti  algoritmi  convergenti  per  il  calcolo  degli  esponenti. 

1.3

L

T

C

D

Il 29 dicembre 1979, il fisico Edward Lorenz  presentò alla Conferenza  annuale  dellʹAmerican  Association  for  the  Advancement  of  Science,    una  relazione  in  cui  ipotizzava  come  il  battito  delle  ali  di  una  farfalla  in  Brasile, a séguito di una catena di eventi, potesse provocare una tromba  dʹaria  nel  Texas[14].  Lʹinsolita  quanto  suggestiva  relazione,  diede  il  nome al cosiddetto butterfly effect, effetto farfalla.  

Nel  corso  di  un  programma  di  simulazione  del  clima,  Lorenz  fece  unʹinaspettata quanto importante scoperta. Una 

delle simulazioni climatiche si basava su dodici  variabili,  incluse  relazioni  non  lineari.  Lorenz  scoprì  che,  ripetendo  la  stessa  simulazione  con  valori  leggermente  diversi,  una  serie  di  dati  veniva prima arrotondata a sei cifre decimali, e  successivamente  a  tre,  lʹevoluzione  del  clima  elaborata dal computer si discostava nettamente  dai  risultati  precedenti:  a  quella  che  si  configurava  appena  una  perturbazione,  dopo  unʹeffimera somiglianza iniziale, si sostituiva un  modello climatico completamente diverso.  Queste  osservazioni  hanno  portato  allo 

sviluppo della Teoria del Caos che pone limiti  definiti alla prevedibilità  dellʹevoluzione di sistemi complessi non lineari.  

Nei  sistemi  lineari,  una  piccola  variazione  nello  stato  iniziale  di  un  sistema fisico, chimico, biologico, o economico provoca una variazione  corrispondentemente  piccola    nel  suo  stato  finale:  per  esempio,  colpendo leggermente più forte una palla da biliardo, questa andrà più  lontano. 

Al  contrario,  sono  non  lineari  le  situazioni  di  un  sistema  in  cui  piccole  differenze  nelle  condizioni  iniziali  producono  differenze  non  prevedibili nel comportamento successivo.  

Un  sistema  può  anche  comportarsi  in  modo  caotico  in  certi  casi  e  in  modo  non  caotico  in  altri.  Per  esempio,  da  un  rubinetto  non  chiuso  le  gocce  cadono  in  una  sequenza  regolare,  variando  leggermente  lʹapertura  del  rubinetto,  si  può  far  sì  che  le  gocce  cadano  invece  in  modo irregolare, appunto caotico.  

Eʹ impossibile prevedere il comportamento che un sistema caotico avrà  dopo un intervallo di tempo anche piuttosto breve. Infatti, per calcolare  il  comportamento  futuro  del  sistema,  anche  se  descritto  da  unʹequazione  molto  semplice,  è  necessario  inserire  i  valori  delle  condizioni iniziali. 

Dʹaltra  parte,  nel  caso  di  un  sistema  complesso  non  lineare,  data  la  grande  sensibilità  del  sistema  agli  agenti  che  lo  sollecitano,  un  piccolo  errore  nella  misura  delle  condizioni  iniziali,  oppure  una  modifica  apparentemente  irrilevante  dei  dati  immessi  ed  ovviamente  anche  il  loro  successivo  arrotondamento  durante  il  calcolo,  cresce  esponenzialmente  con  il  tempo,  producendo  un  radicale  cambiamento  dei risultati. 

Questo  significa  che  i  dati  relativi  alle  condizioni  iniziali  dovrebbero  essere  misurati  con  unʹaccuratezza  teoricamente  infinita,  ma  ciò  é  praticamente impossibile. 

Quanto  detto  spiega  perché  le  previsioni  meteorologiche,  sebbene  descritte con le equazioni deterministiche della fisica, fluidodinamica e  termodinamica, ed elaborate 

con raffinate tecniche di calcolo eseguite da super computer, producono  risultati  molto  approssimativi.    Per  rappresentare  lʹatmosfera  sono  necessari  sei  milioni  di  numeri  e  questo  comporta  i  problemi  connessi  alle misurazioni. Gli strumenti a terra sono molto accurati, ma le sonde  in  quota  possono  rilevare  la  temperatura  con  un  errore  di  un  grado;  i  satelliti pagano lo scotto di sondare spazi altrimenti irraggiungibili con  errori anche di due gradi. 

Lʹeffetto farfalla in conclusione, sottolinea come nella maggior parte dei  sistemi  biologici,  chimici,  fisici,  economici  e  sociali,  esistano  degli  elementi che, apparentemente insignificanti, sono in grado, interagendo 

fra  loro,  di  propagarsi  e  amplificarsi  provocando  effetti  catastrofici.  Questi  elementi,  e  perché  trascurati,  e  perché  imprevedibili,  e  perché  non  individuabili,  costituiscono  il  dilemma  del  nostro  secolo  giacché,  come  visto, possono condurci a conclusioni errate.  

Ecco  il  motivo  per  cui  molto  spesso,  ad  esempio,  per  spiegare  il  comportamento  di  un  sistema  come  la  crescita  della  popolazione,  lʹeutrofizzazione delle coste marine, o le variazioni climatiche, si ricorre  ad un modello. 

Un  modello  è  una  riproduzione  semplificata  della  realtà,  ossia  unʹastrazione  che  considera  solamente  le  principali  caratteristiche  di  quello  che  è  il  reale  oggetto  di  studio.  Tuttavia,  un  modello,  sebbene  possa  sembrare  limitato,  in  quanto  non  riproduce  completamente  la  realtà, permette di esaminare gli aspetti più importanti di un problema.  Dalla  scoperta  di  Lorenz  molto  cammino  è  stato  compiuto  in  tutte  le  branche del sapere. Tra tutte le definizioni create sul 1900, una sembra  la  più  significativa:  il  1900  è  il  secolo  delle  Rivoluzioni.  Dopo  la  Relatività e la Meccanica Quantistica, la rivoluzione più importante è la  scoperta della teoria del Caos. 

Essa  ha  investito  spazi  come  quello  dei  matematici,  una  volta  isolati  e  gelosi  delle    proprie  scoperte,  dei  fisici,  dagli  studiosi  della  meccanica  dei liquidi, agli astronomi, dei chimici e degli studiosi di etologia, degli  informatici e di quanti si occupano di crittografia, dei cardiologi, degli  analisti,  dei  chirurghi,  degli  studiosi  del  comportamento  nellʹorganizzazione aziendale, nella comunicazione o nella geriatria.  In tutte le discipline lo studio del Caos ha dato conferme sorprendenti e  sorprendenti ne sono state finora le conseguenze applicative. Gli studi  di  tutti  gli  scienziati  dimostrano  che  il  comportamento  naturale  dei  fenomeni è non lineare. 

I  comportamenti  della  maggioranza  dei  fenomeni  della  natura  e  dellʹuomo  non  procedono  con  ritmi  che  si  ripetono,  ma,  dopo  un  periodo  regolare,  presentano  in  modo  inaspettato  una  biforcazione  in  un  punto  critico  che  si  moltiplica  fino  a  generare  una  turbolenza.  Un  flusso  regolare  si  scompone  in  vortici  e  mulinelli.  Strutture  irregolari 

interrompono la continuità del confine tra fluido e solido, per esempio  quando il liquido si ghiaccia [15]. 

La  turbolenza  genera  entropia:  mescolanza,  disordine,  casualità.  Tuttavia, le parti scomposte, i vortici nel moto dei fluidi, non fuggono  via, ma restano vicini, pur seguendo regole proprie. 

Ciò avviene per un fenomeno che dà luogo ai cosiddetti attrattori strani.   In poche parole  la turbolenza si produce restando tuttavia allʹinterno di 

una fase. 

Alla  fine  dellʹintero  processo  si  produce  unʹautoorganizzazione  in  una  situazione  nuova,  che  a  sua  volta  può  riprodurre  un  altro  momento  caotico e così via. 

Ciò,  come  già  detto,  è  impredicibile,  sebbene  si  sappia  che  avviene  in  forma rigorosa e deterministica.  

Uno  degli  aspetti  più  interessanti  dello  studio  della  dinamica  dei  sistemi  non  lineari  è  lʹorganizzazione  che  emerge  spontaneamente  dallʹinterazione  di  molte  componenti  elementari  [16].  Un  classico  esempio è quello di un fluido riscaldato dal basso dove in presenza di  opportune  condizioni  al  contorno  i  moti  convettivi  delle  molecole  si  dispongono  secondo  le  cosiddette  colonne  di  Bénard,  che  sono  formazioni  verticali  a  nido  dʹape.  Si  instaura  cioè  unʹinattesa  cooperazione  tra  molecole  laddove  sarebbe  atteso  semplicemente  un  aumento  del  disordine  molecolare.  I  sistemi  complessi  reagiscono  alle  modificazioni  dellʹambiente  esterno  riorganizzandosi  in  modo  da  esibire proprietà innovative. Lʹautoorganizzazione, infatti, è una struttura  spazio‐temporale  che  non  è  imposta  dallʹesterno  ma  emerge  spontaneamente dallʹevoluzione del sistema stesso come funzione della  sua  dinamica.  Lʹorganizzazione  emergente  è  osservabile  ad  una  scala  spazio‐temporale diversa, molto maggiore, da quella molecolare. 

La  costruzione  di  modelli  matematici  per  tali  sistemi  evidenzia  che  le  equazioni  che  li  reggono  sono  in  genere  estremamente  sensibili  alle 

condizioni iniziali, in modo che fluttuazioni estremamente piccole danno 

Questo indeterminismo di fatto, ma non di principio, non è eliminabile,  dato che in un sistema numerico è comunque necessario fissare un certo  grado  di  precisione  non  infinito  e  qualsiasi  grado  anche  più  alto  di  precisione  produrrà  storie  dinamiche  differenti.  Questo  è  il  cosiddetto 

caos  deterministico,  dove  il  sistema  ha  un  comportamento 

complessivamente  regolare  ma  irregolare  nel  dettaglio,  e  quindi  è  impossibile prevedere il suo comportamento negli istanti futuri. 

Si  definisce  allora  il  Caos  come  un  comportamento  non  predicibile  di  un 

sistema  dinamico  deterministico  a  causa  della  sua  sensibilità  alle  condizioni  iniziali [15]. 

Più  precisamente,  un  insieme  S  esibisce  sensibilità  ai  valori  iniziali  se  esiste una ρ  tale che, per ogni ε > 0 e per ogni x in S, esiste un y tale che  |x ‐ y | < ε , e |xn ‐ yn |> ρ per  n > 0. Allora esiste una distanza fissa r 

tale che, per quanto precisamente si specifichi uno stato iniziale, ci sono  stati vicini che alla fine si allontanano di una distanza r.  

Questo è ciò che avviene nei sistemi caotici. Un sistema caotico esibirà  quindi  sensibilità  alle  condizioni  iniziali,  comportandosi  in  modo  complesso. 

Non linearità e sistemi dinamici   

In  natura,  molti  sistemi  sono  lineari  o  approssimabili  alla  linearità,  e  grazie  alla  trasformata  di  Fourier  per  cui  ogni  funzione  matematica  periodica  può  essere  rappresentata  da  una  serie  di  onde  sinusoidali  pure,  si  è  giunti  alla  modellizzazione  di  moltissimi  fenomeni  naturali.  Per  alcuni  sistemi  fisici  la  linearità  non  è  sostenibile,  e  la  loro  modellizzazione  diviene  estremamente  complessa:  quasi  tutti  i  sistemi  dinamici sono caotici, quindi  intrinsecamente deterministici, e di fatto  non predicibili [12] [13]. 

Le funzioni lineari si comportano in modo tale che:    f(ax+by) = af(x) + bf(y).    Nei casi in cui non vale questa eguaglianza, e qui entra in gioco la non  linearità, tutto diviene matematicamente più difficile. Ad esempio se:    f(x) = 0  e  f(y) = 0     per ogni a e b non vale più  f(ax+by) = 0,  perciò la soluzione va cercata  con metodi particolari.  

Nessun  modello  reale  è  veramente  lineare,  ma  spesso  si  può  approssimare  ad  una  funzione  lineare.  I  sistemi  non  lineari  esibiscono  effetti  complessi  non  deducibili  con  metodi  lineari,  caratteristica  particolare  dei  sistemi  dinamici.  Tuttavia,  introducendo  delle  approssimazioni, essi possono essere linearizzati e risolti numericamente  con tecniche tipiche dei sistemi lineari. 

Come  già  anticipato  nel  paragrafo  precedente,  un  sistema  si  dice  sistema  dinamico  quando  esprime  la  variabilità  di  uno  stato,  ossia  un  punto in uno spazio vettoriale, nel tempo:    ( , ) (*) : n n differenziabile dX F X t dt F W R R       

La  soluzione  del  sistema  è  lʹinsieme  delle  traiettorie  in  funzione  delle  condizioni  iniziali.  Un  sistema  dinamico  è  completamente  definito  da  uno spazio delle fasi o degli stati, le cui coordinate lo descrivono in ogni  istante,  e  da  una  regola  che  specifica  lʹandamento  futuro  di  tutte  le  variabili di stato. I sistemi dinamici sono deterministici se esiste un unico  conseguente per ciascuno stato, stocastici se ne esistono diversi con una  certa distribuzione di probabilità come il classico lancio di una moneta. 

Lo  spazio  delle  fasi  è  la  collezione  di  tutti  i  possibili  stati  di  un  sistema  dinamico. Può essere finita, come nel caso della moneta in cui si hanno  due stati, o infinita se le variabili sono numeri reali. 

Matematicamente,  un  sistema  dinamico  è  descritto  da  un  problema  ai  valori iniziali. La curva nello spazio delle fasi tracciata da una soluzione  di  un  problema  ai  valori  iniziali  è  chiamata  traiettoria  del  sistema  dinamico.  

Si  definisce  traiettoria  costante  una  soluzione  costante  x(t)  =  x(0)  di  (*),   ossia un vettore x(0) per il quale ciascuna componente della parte destra  di (*) è zero.  

Una  traiettoria  costante  è  detta  stabile  se  sono  soddisfatte  le  seguenti  condizioni: 

a)  deve  esistere  un  numero  positivo  ε  tale  che,  ogni  traiettoria  che parte allʹinterno di ε di x(0), deve avvicinarsi asintoticamente  a x(0), 

b) per ogni numero positivo ε, deve esistere un numero positivo 

δ(ε),  tale  che,  una  traiettoria  sia  garantita  stare  entro  di  x(0) 

semplicemente richiedendo che abbia inizio entro δ(ε) di x(0), 

c)  lʹinsieme  di  tutti  i  punti  che  possono  essere  stati  iniziali  di  traiettorie  che  si  avvicinano  asintoticamente  ad  una  traiettoria  stabile è detto regione di attrazione della traiettoria stabile. 

Si definisce ciclo limite, o attrattore ciclico,  una curva chiusa nello spazio  n‐dimensionale con le seguenti proprietà: 

a) nessuna traiettoria costante è contenuta nel ciclo limite, 

b)  qualsiasi  traiettoria  che  abbia  inizio  in  un  punto  nel  ciclo  limite deve stare entro il ciclo limite anche in seguito, 

c)  deve  esistere  un  numero  positivo  ε    tale  che  ciascuna  traiettoria  che  abbia  inizio  entro  δ(ε)  del  ciclo  limite  deve  avvicinarsi asintoticamente al ciclo limite, 

d) per ogni numero positivo ε  deve esistere un numero positivo 

δ(ε)  tale  che  una  traiettoria  sia  garantita  stare  entro  e  del  ciclo 

limite semplicemente richiedendo che abbia inizio entro δ(ε) del  ciclo limite. 

In  sintesi,  se  alcune  traiettorie  convergono  in  qualche  punto,  lʹinsieme  degli stati iniziali di tali traiettorie generate è detto regione di attrazione  del punto. Una regione di attrazione è in definitiva un insieme di punti  nello  spazio  degli  stati  di  diametro  finito  tale  per  cui  ogni  traiettoria  entra e non esce più. 

Lʹattrattore,  allora,  può  essere  visto  come  una  generalizzazione  della  nozione  di  equilibrio,  e  rappresenta  ciò  su  cui  si  arresta,  o  verso  cui  è  attratto il comportamento di un sistema. 

Prendiamo  un  comune  pendolo  che  si  muove  sottostando  a  forze  dʹattrito  che  lo  rallentano  fino  a  farlo  fermare.  Si  può  descrivere  il  movimento del pendolo utilizzando il cosiddetto diagramma di fase, o  di  stato,  in  cui  vengano  rappresentati  su  un  asse  lʹangolo  del  pendolo  con  la  verticale  e  sullʹaltro  la  velocità  con  cui  cambia  lʹangolo.  Il  moto  oscillante  del  pendolo  è  allora  rappresentato  da  un  punto  che  gira  intorno  allʹorigine  del  diagramma  di  fase;  man  mano  che  il  pendolo  perde energia, il punto si avvicina a spirale allʹorigine dove infine va a  fermarsi. In questo caso lʹorigine sembra attrarre il punto in movimento  del diagramma di fase. 

Questo è il tipo più semplice di attrattore, il cosiddetto attrattore a punto 

fisso che descrive,  visto, un sistema che evolve sempre verso un singolo 

stato.  Si  passa  poi  alla  forma  più  complessa  di  attrattore,  detta  ciclo 

limite. Esso corrisponde ad un sistema, pendolo ideale senza attriti, che 

evolve  verso  uno  stato  periodico.  Nello  stato  delle  fasi  vicino  al  ciclo  limite  le  traiettorie  seguono  un  percorso  regolare  che  può  essere  circolare o ellittico. 

Altri  attrattori,  definiti  semplicemente  attrattori  strani,  descrivono  sistemi  che  non  sono  né  statici  né  periodici.  Nello  spazio  delle  fasi  vicino  a  un  attrattore  strano,  due  traiettorie  che  presentano  condizioni  iniziali  praticamente  identiche  divergono  rapidamente  e  su  lunghe  distanze  temporali  divengono  molto  differenti.  Un  sistema  la  cui  descrizione  presenta  attrattori  strani  è  caotico  ed  un  tipico  esempio  sono  le  equazioni  di  Lorenz.  Ma  vediamo  più  in  dettaglio  le  caratteristiche delle diverse tipologie di attrattore.      Attrattori puntuali    Lʹattrattore è una figura geometrica nello spazio degli stati cui converge  il vettore di stato di un sistema dinamico, esaurito il transitorio.      Linearizzando nellʹintorno del punto di equilibrio si può dimostrare che  gli  autovalori  della  matrice  Jacobiana  hanno  parte  reale  negativa  e  quindi tale punto è un attrattore puntuale. Scegliendo qualunque stato 

iniziale  la  traiettoria  conseguente  converge  verso  lʹattrattore  seguendo  una linea di flusso dellʹenergia.      Attrattori periodici    Se lo stesso sistema precedente viene polarizzato in modo diverso, per  esempio  sommando  un  opportuno  valore  costante  alla  seconda  curva  isoclina, il punto di equilibrio diventa instabile.  

Esiste tuttavia unʹorbita o ciclo‐limite, verso cui tendono le traiettorie di  stato  a  partire  sia  dallʹinterno  sia  dallʹesterno.  Una  volta  raggiunta  lʹorbita, questa viene ripercorsa periodicamente allʹinfinito. 

La  pendenza positiva nel tratto intermedio della seconda curva isoclina  destabilizza il punto di equilibrio per questa particolare polarizzazione;  tuttavia,  la  pendenza  della  curva  è  negativa  allʹesterno  del  tratto  intermedio e questo è sufficiente a garantire la stabilità in senso lato del  sistema, pur non essendo asintoticamente stabile.      Attrattori caotici o strani   

Il  fatto  di  avere  un  punto  di  equilibrio  instabile,  accoppiato  ad  una  stabilità  alla  Lyapunov  in  senso  lato,  non  implica  necessariamente  la  presenza di un attrattore periodico.  

Si  consideri,  ad  esempio,  il  sistema  dinamico  non  lineare  di  ordine  3  (sistema di Lorenz): 

1 2 3 ( , , ) ( ) ( , , ) ( , , ) dx f x y z y x dt dy f x y z rx xz y dt dz f x y z xy bz dt               

Il  sistema  è  costituito  di  tre  equazioni  differenziali  di  primo  ordine  in  forma  normale  nelle  variabili  x,  y  e  z.  Lo  spazio  delle  fasi  è  tridimensionale,  e  le  variabili  (x,y,z)  non  sono  variabili  spaziali,  ma  legate  ai  campi  di  velocità  e  temperatura  di  un  fluido  in  moto  convettivo (σ, b e r sono parametri idrodinamici che possono assumere  solo valori positivi). 

Durante  lo  studio  del  sistema  precedente,  Lorenz  si  accorse  di  un  andamento  non  periodico,  mentre  allora  si  riteneva  che  il  comportamento  tipico  di  un  sistema  di  equazioni  differenziali  fosse  quello periodico. Volendo ricontrollare i dati ottenuti fino allʹistante T,  decise di ripetere lʹintegrazione numerica, e per risparmiare tempo non  scelse la condizione iniziale (x (0), y (0), z (0)), ma un punto intermedio 

tʹ  <  T,  le  cui  coordinate  erano  già  state  stampate  dal  calcolatore. 

Ovviamente  si  aspettava  di  ritrovare  gli  stessi  punti  già  ottenuti  nellʹintervallo  [tʹ,T],  ma  ciò  non  si  verificò.  Con  suo  grande  stupore  constatò infatti che la causa di questa discrepanza non era attribuibile a  errori  di  integrazione,  bensì  soltanto  a  valori  iniziali  leggermente  diversi:  mentre  nella  prima  integrazione  il  punto  (x(tʹ),  y(tʹ),  z(tʹ))  era  stato memorizzato con sei cifre significative, nel ripetere lʹintegrazione,  la seconda volta, Lorenz ne ricopiò soltanto tre.  

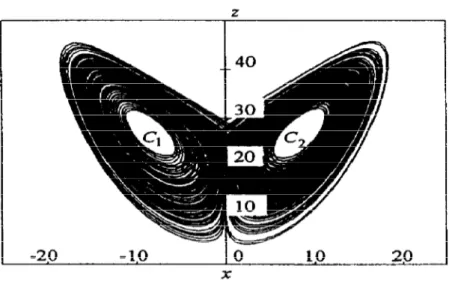
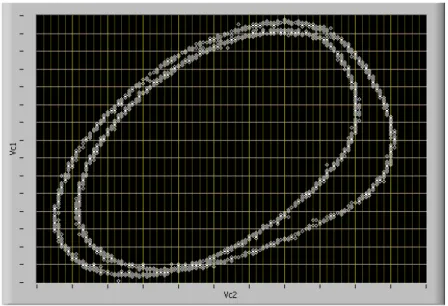
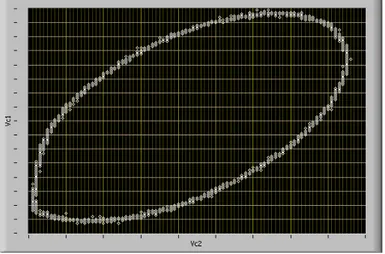
In  figura  1.4  (pag.  seguente)  è  mostrato  il  tipico  attrattore  di  Lorenz,  come proiezione della traiettoria nel piano x. 

I punti C1 e C2 rappresentano punti instabili per  il sistema considerato. 

La  soluzione  si  muove  con  percorso  a  spirale  attorno  ad    uno  dei  due  punti  fissi,  per  poi  passare  ad  avvolgersi  attorno  all’altro  sempre  con  moto  a  spirale.  Tale  andamento  si  ripete  all’infinito,  ed  il  numero  di  rivoluzioni  attorno  ad  un  punto  fisso,    prima  di  alternarsi,  varia  in  maniera apparentemente randomica.  

Figura 1.4: Attrattore caotico di Lorenz 

Riassumendo:    un  particolare  sistema  deterministico  può  generare  un  comportamento  caotico  inteso  come  comportamento  aperiodico,  duraturo  nel  tempo,  delle  proprie  traiettorie.  In  tal  caso,  a  causa  della  dipendenza  sensibile  dalle  condizioni  iniziali,  si  possono  avere  traiettorie che non raggiungono punti di equilibrio e non si chiudono su  cicli limite, ma continuano a muoversi nello spazio di stato presentando  oscillazioni    non  periodiche  non  determinabili  a  priori.  In  base  alle  condizioni iniziali degli elementi il sistema può volgere verso una certa  direzione lungo le traiettorie ed evolvere verso la stabilità o l’instabilità.  In  un  circuito  elettronico  autonomo,  come  quello  di  Chua  oggetto  del  presente lavoro,  questo comportamento non è dovuto a fattori forzanti  esterni ma è una proprietà intrinseca del sistema caotico. 

1.4 C

S

C

Come  appena  visto,  una  delle  caratteristiche  più  conosciute  di  un  sistema  caotico  è    la  sua  sensibilità  alle  condizioni  iniziali.  Si  rivelò  quindi sorprendente la scoperta ottenuta da Pecora e Carroll, i quali per  primi  mostrarono  che  sistemi  caotici  possono  essere  sincronizzati  inviando solo una parte delle informazioni relative allo spazio di stato  da  un  sistema  all’altro  [25].  Dopo  poco  fu  suggerito  di  usare  questo  risultato  per  creare  chiavi  crittografiche,  costruite  con  le  informazioni  dello  spazio  di  stato  non  inviate  per  la  sincronizzazione;  un  primo  utilizzo  di  quest’idea  avvenne  per  l’equazione  di  Lorenz.  L’idea  alla  base è che accedere al messaggio risulta impossibile senza conoscere i tre  parametri  dell’equazione,  e  per  questo  motivo  tale  insieme  è  detto 

super‐chiave. 

Tuttavia questo sistema si rivela facilmente violabile e la super‐chiave si  può  determinare  rapidamente  dal  segnale  di  sincronizzazione.  Altre  soluzioni  che  rendono  più  efficace  e  sicuro  questo  sistema  da  attacchi 

esterni sono state studiante del corso degli anni [22] [23][24], ed esse si  basano  sulla  riduzione  della  durata  del  segnale  di  sincronizzazione,  fornendolo periodicamente nel tempo; ciò comporta tuttavia un ritardo  nel raggiungimento della condizione di sincronizzazione. 

Il  requisito  di  sicurezza,  fondamentale  nella  crittografia,  rientra  naturalmente  anche  nella  crittografia  caotica,  e  costituisce  una  motivazione  importante  per  la  ricerca  nel  campo  della  comunicazione 

caotica.  Pertanto,  diverse  tecniche  sono  state  supposte  e  sviluppate, 

quali  masking  con  segnale  caotico  aggiuntivo,  switching  caotico,  e 

modulazione con portante caotica. Questo per sistemi a tempo continuo. 

Sviluppi  in  ambito  dell’elettronica  digitale  sono  stati  altresì  proposti,  primo  fra  tutti  l’utilizzo  di  sistemi  caotici  per  generare  sequenze  numeriche random (RNG) utilizzabili come chiavi o maschere del testo  in chiaro. Tuttavia, l’implementazione numerica non gode di particolari  vantaggi rispetto al caso analogico. Poiché i calcolatori sono in grado di  rappresentare le cifre con una precisione finita, qualunque tipo di orbita  di un attrattore caotico, in uno spazio delle fasi a dimensione finita sarà  necessariamente  periodica.  In  altre  parole,  non  è  possibile  generare  il  caos con sistemi a stati finiti. Si avrà pertanto una periodicità del sistema  (e da qui la definizione di PRNG, pseudo‐random numbers generator),  e quindi una maggiore vulnerabilità da attacchi esterni. 

C

APITOLO 

2 

I

L 

C

IRCUITO DI 

C

HUA 

2.1 P

C

C

? 

Il  circuito  di  Chua    è  un  circuito  elettronico  non  lineare,  e  sin  dal  suo  sviluppo nel 1983 ad opera del prof. Leon 

O.Chua  (figura  2.1  ),  docente  dell’università della California, Berkeley, è  stato  oggetto  di  numerose  attività  di  ricerca  scientifica.  Esso  ha  il  pregio  di  essere  l’unico  circuito  autonomo  in  cui  la  presenza  del  caos  è  stata  provata  in  maniera analitica, tanto da essere definito  a universal paradigm for chaos.  

Prima  del  1983,    nessun  circuito  elettronico  autonomo  aveva  mostrato  comportamento  caotico,  nonostante  gli 

sforzi del prof. Matsumoto di realizzare un circuito analogico a partire  dalle  equazioni  di  Lorenz.  Nel  1984  fu  lo  stesso  Matsumoto  a 

dimostrare l’intriseca caoticità di un circuito realizzato dal suo collega, e  da  lui  stesso  battezzato  circuito  di  Chua,  mediante  simulazioni  al  calcolatore  (  [1]  e  [2]  ).  La  verifica  sperimentale  del  comportamento  caotico arrivò  pochi mesi dopo, ad opera di Zhong ed Ayrom [3].    

Nel corso degli anni, e fino ai giorni nostri, sono stati sviluppati diversi  modelli  e  varianti  del  circuito  in  questione.  Una  delle  soluzioni  più  gettonate è quella di realizzare il componente non lineare (il cosiddetto  Diodo di Chua, che consente  il comportamento caotico del circuito), in  maniera  semplice  ed  economica  mediante  una  coppia  di  amplificatori  operazionali e sei resistori di polarizzazione [4]. 

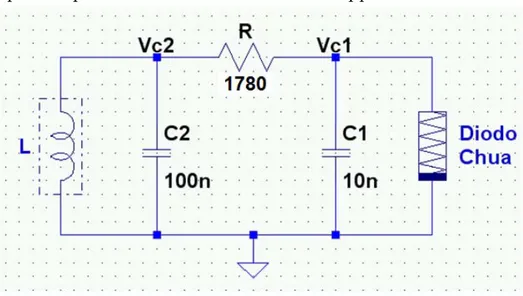
Grazie  al  basso  costo  ed  alla  efficienza  pratica  il  circuito  di  Chua  è  divenuto  il  circuito  di  riferimento  per  applicazioni  che  richiedono  una  sorgente di segnale caotico robusta ed economica.          Figura 2.2: Il circuito di Chua

2.2 A

C

Il circuito di Chua contiene quattro elementi lineari (due condensatori,  un induttore ed un resistore) ed un resistore non lineare. Ha pertanto i  requisiti  minimi  necessari  (ma  non  sufficienti)  affinchè  presenti  comportamento caotico: 

 almeno tre componenti  dinamici,   almeno un componente non lineare,   almeno un componente attivo. 

La  sua  peculiarità  di  essere  un  circuito  autonomo  fa  sì  che  non  sia  necessario  pilotarlo  mediante  una  tensione  ac.  Partendo  dal  presupposto  che  il  resistore  R,  l’induttore  L,  e  i  condensatori  C1  e  C2  

assumano  valori  nominali  positivi,  risulta  necessario  che,  affinchè    il  circuito oscilli o esibisca comportamento caotico, l’elemento non lineare  sia attivo. 

Ciò  vuol  dire  richiedere  che  la  sua  caratteristica  tensione‐corrente  appartenga  almeno  per  alcuni  tratti  al  secondo  e  quarto  quadrante,  dove  il  prodotto  v*i  risulta  negativo,  e  quindi  che  l’elemento  in  considerazione  fornisca  energia  agli  elementi  passivi.  Però,  visto  che  nessun dispositivo fisico è in grado di fornire una quantità di potenza  infinita,  la  scelta  di  una  caratteristica  v*i  fisicamente  realizzabile  deve  ricadere sulla caratteristica di un bipolo asintoticamente passivo. 

Il  circuito  di  Chua  rappresentato  in  figura  potrà  allora  esibire  comportamento  caotico.  In  particolare,  modificando  il  valore  del  resistore  lineare,    sarà  possibile  scorrere  la  gamma  delle  possibili  dinamiche  di questo circuito, che esibisce una varietà  di biforcazioni e  di andamenti caotici. 

Il  circuito  sopra  mostrato  è  caratterizzato  da  tre  variabili  di  stato,  e  pertanto può essere descritto dalle seguenti equazioni circuitali: 

Figura 2.3: Caratteristica del diodo di Chua









− f(vC1)  rappresenta  la  caratteristica  tensione‐corrente  del 

componente  non  lineare,  approssimata  come  detto  con  una  spezzata lineare a tratti. 

Quest’ultima  ha  la  seguente  espressione,  con  l’andamento  riporato  in figura:  









A  partire  da  tali  equazioni,  è  possibile  adiamensionalizzare  il  sistema  per poterlo trattatare in unaforma più maneggevole nel seguente modo: