1.
2.
3.
Condizioni di equilibrio per il velivolo rigido
4. ANALISI DELLE CONDIZIONI DI EQUILIBRIO DEL
VELIVOLO RIGIDO.
4.1 - INTRODUZIONE.
Nella prima fase di questo lavoro si analizzano tutte le possibili situazioni di volo in cui può trovarsi il velivolo, ritenute significative e compatibili con le proprietà di funzionamento della macchina, delle quali se ne ha in parte conoscenza come indicato nel paragrafo 3.4, con lo scopo di determinare le caratteristiche aerodinamiche del velivolo in condizioni di equilibrio, in termini di:
• Coefficiente di portanza complessivo del velivolo. • Coefficiente di resistenza complessivo del velivolo. • Spinta propulsiva necessaria.
Mediante un calcolo iterativo si determina l’angolo d’incidenza, rispettivamente, del gruppo ala-fusoliera e della coda orizzontale, al fine di conoscere anche le caratteristiche aerodinamiche della sola coda orizzontale nelle medesime condizioni di volo, ovvero il proprio coefficiente di portanza e di resistenza (CLtail,CDtail).
4.2 - PARAMETRI CARATTERISTICI DELLE CONDIZIONI DI VOLO. Una generica condizione di volo è definita dai seguenti parametri:
• Quota di volo.
• Numero di mach di volo (ovvero velocità di volo). • Peso del velivolo.
I valori del mach presi in esame, vincolati dai dati relativi alla macchina disponibili, permettono di studiarne il comportamento sia alle basse velocità a bassa quota, sia alle alte velocità ad alta quota. Non viene considerato il caso di volo ad alta velocità a bassa quota in quanto, generalmente, non consentito.
In quest’analisi viene assunta un’escursione del baricentro tra una posizione “tutto avanti”, corrispondente al 15 % della corda media aerodinamica dell’ala, ed una “tutto dietro”, corrispondente al 45 % della corda media aerodinamica. Vengono studiate tre distinte situazioni:
1. Baricentro al 15 % della corda media aerodinamica dell’ala. 2. Baricentro al 25 % della corda media aerodinamica dell’ala. 3. Baricentro al 45 % della corda media aerodinamica dell’ala.
Nella condizione relativa al punto 2, si ha la coincidenza del centro di gravità del velivolo con il centro aerodinamico dell’ala, definito come il punto situato ad un quarto della corda media aerodinamica dell’ala a partire dal proprio bordo d’attacco.
Al fine di considerare tutte le possibili combinazioni dei due parametri: quota, peso, si definisce un’unica variabile, W /δ , come rapporto tra il peso del velivolo ed il rapporto, δ , tra la pressione alla generica quota, p , e quella al livello del mare, : p0
0
p p
=
δ
In questo modo, facendo variare W/δ tra un valore minimo ed uno massimo, per ogni valore del mach e della posizione del baricentro che sono stati presi in considerazione, si possono individuare tutte le possibili condizioni operative equilibrate per il velivolo e determinare le relative curve equilibrate CL = f
( )
α per mezzo di un opportuno calcolo iterativo fatto sulla forza di portanza del gruppo ala-corpo e sull’angolo d’incidenza della coda orizzontale. In figura 4.1 viene mostrato l’andamento del peso W con la quota di volo, per fissati valori del parametro W/δ .Condizioni di equilibrio per il velivolo rigido
Fig. 4.1: Andamento del peso Wcon la quota di volo per fissati valori del parametro
δ
W
4.3 - COEFFICIENTI C E D0 K RELATIVI AL VELIVOLO.
Il calcolo del coefficiente di resistenza del velivolo per portanza nulla e del coefficiente che determina la resistenza indotta dalla portanza, è svolto a partire dai dati sperimentali a disposizione, quali la polare del velivolo per una condizione di volo a bassa velocità
e le curve equilibrate
(
M =0.20)
CD = f( )
M , parametrizzate in funzione del rapportoδ
/
W , per il volo ad alta velocità.
Per la condizione di volo a M =0.20, i valori adottati sono quelli sperimentali esplicitamente forniti, mentre per valori del mach compresi tra 0.50 e 0.75, sono dedotti analiticamente per la prefissata coppia di valori
(
W/δ,M)
, imponendo una condizione di equilibrio in termini di uguaglianza portanza-peso. Determinato il valore del coefficiente di portanza come precedentemente discusso, dalle seguenti relazioni derivano i coefficienti cercati. A tale fine è necessaria una stima del coefficiente di Oswald e: questa viene fatta sulla base di un opportuno metodo reperito dalla letteratura nel riferimento [1].L C M p S W 2 0) ( 2 1 γ δ = K π AR e 1 = 2 0 D L D C KC C = −
La validità circa la stima del coefficiente di Oswald mediante il metodo adottato, è confermata dal valore ottenuto del parametro K che, confrontato con il valore
sperimentale noto per , consente di ritenere costante tale coefficiente nel campo dei valori del mach d’interesse in tale studio. Nella tabella 4.1 sono indicati i valori ottenuti per i coefficienti in questione.
20 . 0 = M M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 0 D C 0.021700 0.022299 0.021822 0.022332 0.022990 K 0.049137 e 0.781
Condizioni di equilibrio per il velivolo rigido 4.4 - COEFFICIENTI E RELATIVI ALLA CODA ORIZZONTALE
DEL VELIVOLO. tail D
C 0 Ktail
Il calcolo del coefficiente di resistenza a portanza nulla per la sola coda orizzontale è svolto valutando preliminarmente il coefficiente di attrito equivalente della superficie portante nelle diverse condizioni di volo (rif. [2]). Ciò richiede la conoscenza del numero di Reynolds , funzione della quota e della velocità del velivolo, oltre che della geometria della superficie considerata ed in particolare di una propria dimensione caratteristica, che, per questo caso, si assume essere la corda media aerodinamica dello stabilizzatore
( )
Rtail
c . Assumendo che la superficie della coda orizzontale sia interessata per
circa il 5 % da un flusso laminare e per il restante 95 % da un flusso turbolento, a partire dai relativi coefficienti d’attrito definiti sulla base del valore del Reynolds, è possibile individuare il coefficiente d’attrito complessivo equivalente.
Il coefficiente d’attrito associato ad un flusso laminare, che investe una porzione limitata della superficie, è stimato con:
R CL f 328 . 1 = (flusso laminare)
La stima per un flusso turbolento si basa sulla seguente relazione:
65 . 0 2 58 . 2 (1 0.144 ) ) (log 455 . 0 M R CT f = + (flusso turbolento)
Complessivamente si assume un coefficiente d’attrito equivalente pari a: T f L f f C C C =0.05 +0.95 M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 f C 0.002469 0.002082 0.002071 0.002091 0.002087
Il valore del Reynolds da adottare nelle precedenti relazioni deve essere il minore tra il Reynolds di “cut-off” e quello reale i quali devono essere opportunamente valutati. Il Reynolds di “cut-off“ è calcolato tenendo conto che il materiale con cui è realizzata la superficie è alluminio, tale da renderla non eccessivamente rugosa. Per il calcolo del Reynolds reale si considerano tutte le possibili combinazioni di valori: quota di volo, mach di volo, forniti dalla curva inferiore dell’inviluppo di volo del velivolo, la quale può essere individuata già in questa fase dello studio. Così facendo, ne consegue che il Reynolds di “cut-off“ è sempre abbondantemente maggiore dei valori del numero di Reynolds reale calcolati per ciascuna condizione di volo esaminata. Dunque, il Reynolds reale calcolato assume, per ogni mach considerato, il minimo valore possibile, quindi è quello utilizzato per valutare i coefficienti d’attrito.
Trattandosi di un velivolo con piano di coda a T, in cui la superficie orizzontale della coda è posta al di sopra della superficie delle ali, si può ritenere in prima analisi che la superficie dello stabilizzatore non sia interessata da fenomeni d’interazione con la scia fluida che si stacca dalla superficie alare primaria. Per la posizione del piano di coda, si può assumere che la superficie bagnata dello stabilizzatore sia approssimativamente il doppio della superficie di riferimento dello stesso. Per tenere conto di tale approssimazione, il coefficiente di resistenza a portanza nulla può essere ottenuto effettuando una maggiorazione del coefficiente d’attrito complessivo di circa il 2%. Dunque, considerando il contributo fornito sia dalla superficie dorsale che ventrale, il coefficiente di resistenza parassita totale della superficie orizzontale risulta:
f tail
D C
C 0 = 022. ⋅
Il coefficiente relativo alla sola coda è valutato in modo analogo a quanto fatto per l’intero velivolo, una volta determinato l’allungamento alare della coda ( ) e stimato il relativo valore del coefficiente di Oswald, secondo la medesima procedura illustrata nel riferimento [1]. Inoltre, in analogia a quanto affermato circa il valore del coefficiente
tail K
tail AR
K
associato all’intero velivolo, anche per il solo piano di coda orizzontale, si ritiene che il valore del coefficiente ad esso relativo si mantenga costante al variare del numero di mach. Nella tabella 4.3 sono indicati i valori ottenuti per i coefficienti in questione.
tail K
Condizioni di equilibrio per il velivolo rigido Si fa notare che già in questa fase del lavoro si traccia la curva inferiore dell’inviluppo di volo, riportata in figura 4.2, valutata nella condizione di maggior peso possibile per il velivolo, pari a 77700 Lb. La ricostruzione di tale ramo dell’inviluppo è resa possibile utilizzando la curva, riportata nel manuale di volo di tale velivolo, che descrive il legame sperimentale tra la quota e la velocità vera di volo, rispettando opportuni vincoli sulla base della quota operativa: fino ad un’altezza di 26000 Ft, si assume che il volo sia effettuato ad una velocità indicata costante pari alla massima velocità operativa di 350 Kt, mentre, per quote superiori a 36000 Ft, fino a circa 50000 Ft, si assume di volare ad un valore del mach costante pari a 0.84 (mach di “drag–rise”); per quote intermedie, comprese tra 26000 Ft e 36000 Ft, la curva sperimentale ha un andamento lineare decrescente. Nella medesima figura 4.2 sono contrassegnati i punti direttamente ottenuti dai dati sperimentali.
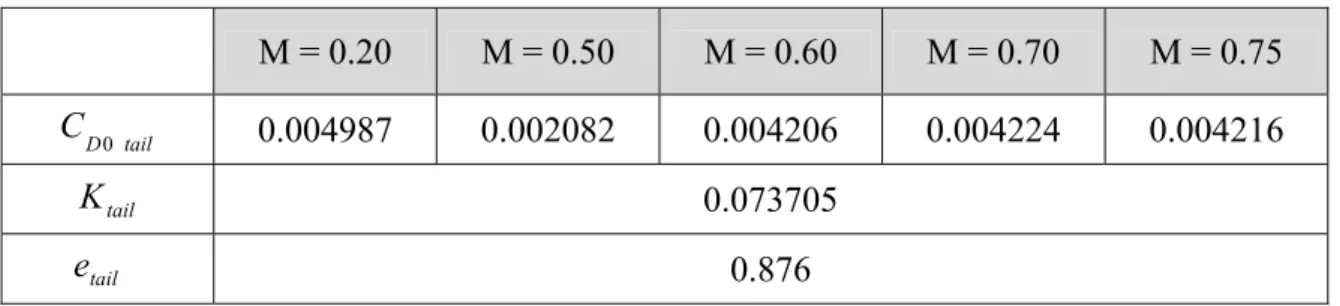
M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 tail D C 0 0.004987 0.002082 0.004206 0.004224 0.004216 tail K 0.073705 tail e 0.876
Tab. 4.3: Valori di CD0tail, Ktail, e per distinti numeri di mach. tail
4.5 - PENDENZA DELLA CURVA DI PORTANZA DELLA CODA ORIZZONTALE.
Per la valutazione del parametro dapprima si adotta una relazione semi-empirica in cui si assume che la velocità del flusso che investe la coda sia coincidente con quella del flusso asintotico, senza considerare quindi l’interferenza della scia dell’ala. Tale relazione discussa in [2] ha lo scopo di fornirne un valore abbastanza preciso, risultando sufficientemente accurata per condizioni di volo fino al mach di “drag-rise“.
tail L
C α
Successivamente, invece, sfruttando i dati a disposizione derivanti da prove sperimentali, si determina il reale valore della pendenza della curva di portanza della sola coda in cui viene implicitamente inglobato l’effetto dell’interferenza generato dall’ala, indicato con . Ciò consente di valutare quale sia il rapporto tra la velocità che possiede il flusso asintotico che investe l’ala e quella del flusso che investe la coda, influenzata dalla presenza della superficie alare anteriore.
tail a
Secondo la suddetta procedura, la pendenza della curva di portanza della superficie posteriore è data dalla seguente relazione:
(
)
( )
F S S AR AR C ref t ex t t tail tail tail L Λ + + + = 2 max 2 2 2 tan 1 ) ( 4 2 2 β η β π α rad 1 Valgono:Condizioni di equilibrio per il velivolo rigido 2 2 =1−M β 1.07 1 1 2 ≅ + = tail fus b d F π η α 2 tail l C =
Il termine rappresenta l’angolo di freccia della superficie orizzontale di coda in corrispondenza del massimo spessore del profilo: esso risulta pari a 35 [deg]. Relativamente ai rimanenti termini che compaiono nella precedente espressione del
, occorre precisare che t
max Λ
(
CLα)
tail β risulta funzione esclusivamente del mach relativo allacondizione di volo considerata, il “fuselage-lift-factor“ , che tiene conto della interferenza esercitata dalla fusoliera sulla superficie portante considerata, per la geometria del piano di coda può essere assunto pari ad 1. Inoltre, l’efficienza del profilo
F
η dipende dalla pendenza della curva di portanza del semplice profilo che caratterizza la superficie portante di coda. Non disponendo di informazioni più accurate sulla forma di tale profilo, si assume che esso sia simmetrico del tipo NACA 0009 con un pari a 5.4435 [1/rad]. Infine, essendo la superficie di riferimento del piano di coda orizzontale diminuita della porzione coperta dalla fusoliera, per quanto già discusso, il rapporto tra le superfici ed risulta pari ad 1. I valori del ottenuti sono indicati nella tabella 4.4 tail l Cα ex S ex t S Stref CLαtail M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 tail L C α 3.42241 3.79073 3.99359 4.23207 4.35914
Tab. 4.4: Valori del CLαtail ottenuti dal modello “Raymer” per distinti valori del mach.
La valutazione del parametro in questione
(
CLα)
tail mediante i dati sperimentali a disposizione, richiede invece un’analisi dell’equazione d’equilibrio al momento per l’intero velivolo, calcolata rispetto al baricentro considerato coincidente con il punto corrispondente al 25 % della corda media aerodinamica dell’ala a partire dal bordod’attacco (generalmente definito centro aerodinamico dell’ala), in cui si introducono tutti i contributi alle forze ed ai momenti forniti dalle superfici portanti. Infatti, definito il momento complessivamente agente, differenziandolo e linearizzandolo rispetto all’angolo d’incidenza della coda, è possibile valutare la relativa espressione del coefficiente C , il cui valore è sperimentalmente noto. Essendo il valore del coefficiente C funzione della pendenza della curva di portanza della coda, sulla base di alcune ipotesi di lavoro semplificative ma abbastanza realistiche, ne consegue direttamente il reale valore del che tiene conto implicitamente degli effetti della velocità, definito come sopra precisato . S Mα S Mα tail L C α tail a
)
S αI contributi al momento dipendenti dall’angolo d’attacco della coda sono:
(
t S t S)
t(
t S tt X Z D Z X
L
M =− cosα + sinα + cosα − sin
L’ipotesi di coda con profilo simmetrico e privo di svergolatmento, consente di ritenere nulli la forza ed il momento aerodinamici legati alla curvatura del profilo, quando questo ha incidenza nulla (CL0 tail =0, M025tail =0
S
). Stimare che siano presenti valori sufficientemente piccoli dell’angolo α , consente di approssimare il coseno dell’angolo all’unità ed il seno all’angolo stesso. Il differenziale del momento complessivo rispetto all’angolo d’incidenza della coda può essere espresso nella seguente forma:
S M S C c S q M α α = ∂ ∂
Procedendo come detto ed esplicitando i coefficienti si può scrivere:
( )
(
M)
D tail t t sper tail C C X S c S a =− αS − 0Condizioni di equilibrio per il velivolo rigido VALORI SPERIMENTALI M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 S M C α -0.0690 -0.0740 -0.0780 -0.0830 -0.0860
( )
atail sper 3.91769 4.26743 4.51228 4.81457 4.99733 Tab. 4.5: Valori sperimentali dei coefficienti( )
atail sper, CMαS.La differenza tra i valori teorici ottenuti con il modello semi-empirico e quelli sperimentali è da attribuire alla variazione di velocità tra il flusso asintotico che investe l’ala e quello che investe direttamente la coda, quindi alla differenza tra il numero di mach rispettivamente sull’ala e sulla sola coda orizzontale. In questo caso è possibile definire un parametro ηt come il quadrato del rapporto tra il valore del mach in corrispondenza rispettivamente della coda e dell’ala, da valutare come rapporto tra i valori sperimentali
( )
(
atail sper)
e quelli teorici(
CLαtail)
. Dunque, si può scrivere:( )
= 22 V V C a tail tail L sper tail α 2 2 2 2 M M V Vtail tail t = = ηNoti i valori del parametro ηt per ogni mach considerato, si può individuare un coefficiente correttivo medio
( )
ηt al fine di fornire una correzione media dei risultati teorici sulla base di quelli reali: i risultati ottenuti sono indicati nella tabella 4.6.M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 t
η 1.0699 1.0610 1.0628 1.0666 1.0707
( )
ηt 1.0662Nelle figure 4.3, 4.4, 4.5 che seguono, sono riportati rispettivamente gli andamenti del coefficiente teorico , del coefficiente teorico C soggetto ad una correzione media pari a
tail L
C α Lαtail
( )
( )
ηt =1.0662 e del coefficiente sperimentale( )
atail sper, al variare del numero di mach, ottenuti mediante interpolazione dei valori conseguiti in corrispondenza dei mach analizzati e contrassegnati in ciascuna figura. Inoltre, è rappresentato l’andamento dell’errore dovuto alla correzione media dei risultati teorici che evidenzia come il valore del C “mediamente corretto“ si allontani dal valore sperimentale. Ne consegue che i risultati ottenuti secondo le considerazioni fino ad ora svolte forniscono un’ottima approssimazione.tail Lα
A fronte di quanto raggiunto in questa fase, è possibile ritenere che la velocità del flusso fluido che investe la sola coda ha un modulo maggiore di circa il 6 % rispetto al modulo della velocità posseduta dal flusso asintotico che investe direttamente l’ala; inoltre, rispetto al vettore della velocità del flusso indisturbato, ne risulta una rotazione relativa significativa del vettore della velocità del flusso in coda, ovvero una variazione della direzione secondo la quale la superficie di coda viene investita dal fluido.
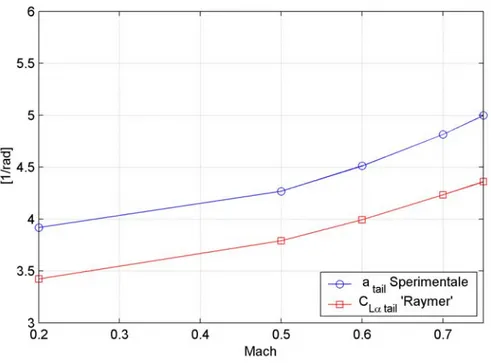
Fig. 4.3: Andamento del coefficiente teorico CLαtail e sperimentale
( )
atail sper al variare del numero di mach.Condizioni di equilibrio per il velivolo rigido
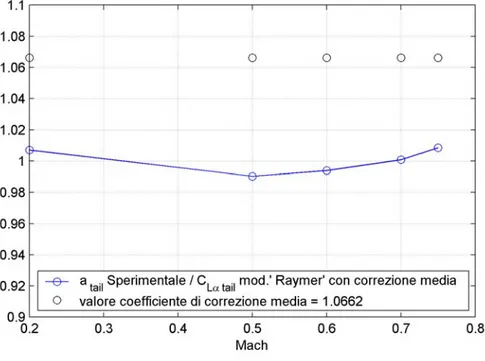
Fig. 4.4: Andamento del coefficiente teorico CLαtail corretto per mezzo del coefficiente ηt, e del coefficiente sperimentale
(
atail)
sper al variare del numero di mach.4.6 - CONDIZIONI DI EQUILIBRIO A FATTORE DI CARICO UNITARIO.
Il calcolo dei coefficienti di portanza e di resistenza dell’intero velivolo nella condizione di volo rettilineo equilibrato (a fattore di carico n unitario) con pendenza della traiettoria nulla viene svolto imponendo l’equilibrio delle forze agenti complessivamente sul velivolo, rispettivamente secondo la direzione longitudinale
Z
( )
XS e verticale del sistema di riferimento in assi stabilità mediante le equazioni 1 e 2 (sotto riportate). Inoltre, noti i coefficienti C e(
ZS)
0D K in precedenza calcolati, assumendo per il velivolo una polare di forma parabolica è possibile conoscere il legame tra gli stessi coefficienti. In questo modo, si ottiene il sistema di tre equazioni nelle tre incognite: CLtrim, CDtrim, Teng /δ , di seguito riassunto. Si osserva che il valore della spinta che il motore deve necessariamente erogare è rapportato, come il peso del velivolo, al parametro δche dipende dalla quota di volo. Per calcolare tale rapporto Teng /δ occorre risolvere un’equazione di secondo grado derivante dal sistema di equazioni suddetto. Delle due soluzioni ottenute viene scartata quella che richiederebbe all’apparato propulsivo una spinta eccessivamente alta, assolutamente non erogabile dal motore di questo velivolo e non compatibile con la resistenza posseduta dalla macchina.
1. sin
( )
+ − eng cos( )
eng =0 Z T D n W α δ δ γ δ2. − cos
( )
+ eng sin( )
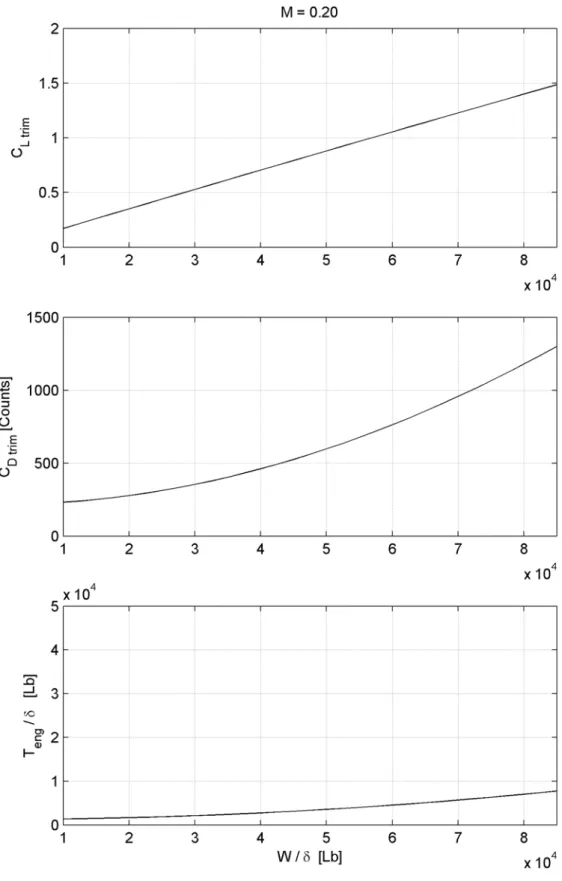
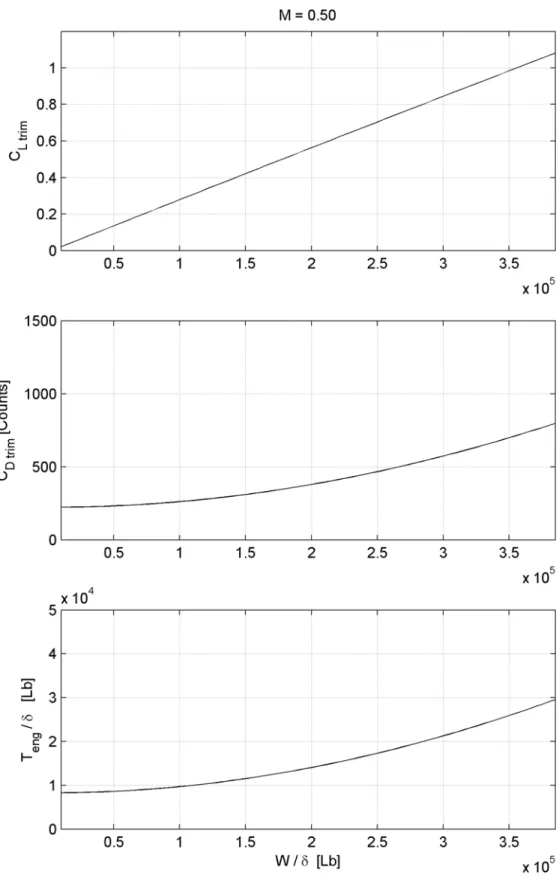
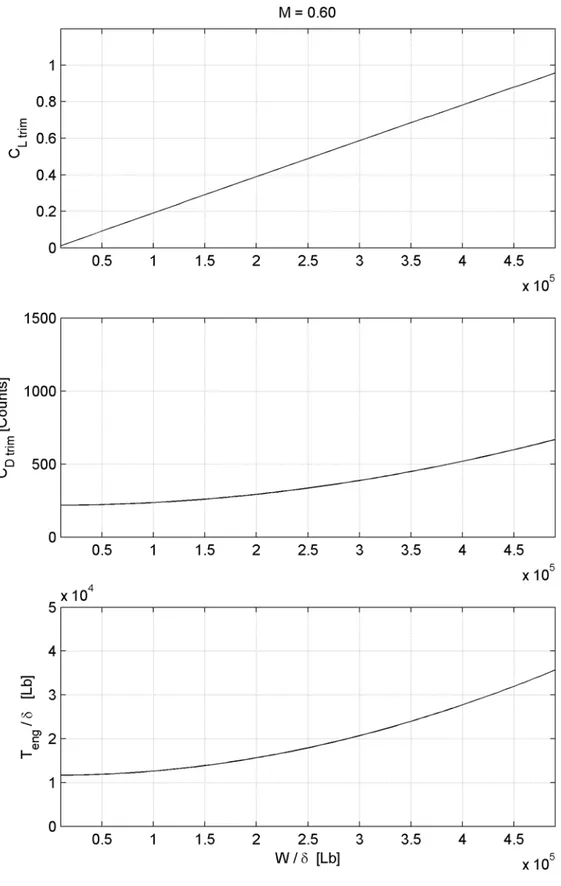
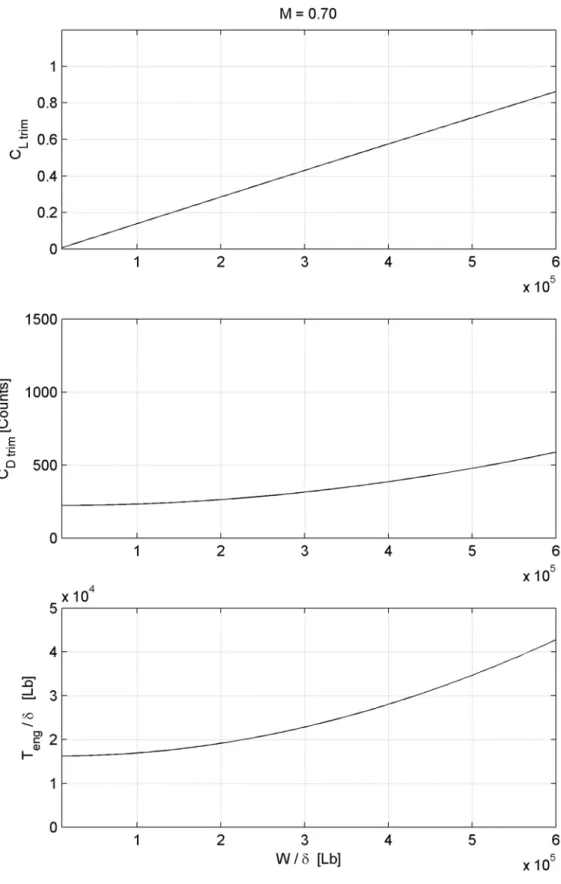
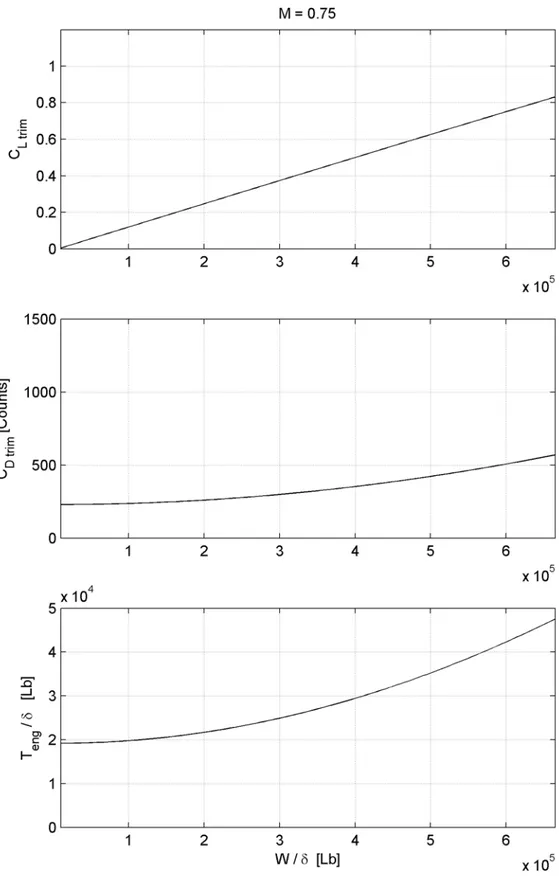
eng =0 Z T n W L α δ γ δ δ 3. 2 0 Ltrim D trim D C KC C = +Nelle seguenti figure 4.6 – 4.10 sono illustrati gli andamenti delle soluzioni del sistema di equazioni discusso, in funzione del parametro W/δ e per condizioni di volo a mach costante. Dalla loro analisi si riscontra una diminuzione di C e ed un contemporaneo aumento della spinta necessaria, con l’aumentare del mach.
trim
Condizioni di equilibrio per il velivolo rigido
Condizioni di equilibrio per il velivolo rigido
Condizioni di equilibrio per il velivolo rigido
4.7 - CALCOLO DELLA FORZA DI PORTANZA AGENTE SULL’ALA E DELL’ANGOLO DI INCIDENZA DELLA CODA IN CONDIZIONI DI EQUILIBRIO.
Note la forza di portanza e di resistenza totali agenti sul velivolo in condizioni d’equilibrio e la spinta motore necessaria, per ogni valore del mach analizzato e per ciascuna posizione del baricentro considerata si passa a determinare il contributo alla forza portante complessivamente agente fornito dal sistema ala-corpo, al fine di valutare la forza di portanza che compete alla sola superficie di coda orizzontale, ottenuta come differenza tra le due precedenti quantità. A partire dalle curve sperimentali CLwb = f
(
αwb)
e(
Lwb)
wb
M f C
C 025 = fornite per distinti valori del numero di mach, mediante l’implementazione di un opportuno calcolo iterativo si definisce il reale valore della portanza generata dal gruppo ala-fusoliera assumendo, ad inizio ciclo, che sia pari alla forza portante complessiva necessaria per l’equilibrio. Successivamente tale valore viene iterativamente aggiornato in seguito al calcolo della forza di portanza in coda, fino al raggiungimento della convergenza al valore finale, avendo prefissato un margine d’errore ε dell’ordine di 0.1 % come tolleranza. La componente , ovvero il coefficiente di portanza del gruppo ala-fusoliera
wb L
(
CLwb)
, consente di conoscere relativamente al medesimo gruppo, per mezzo delle due curve menzionate sopra, rispettivamente: l’angolo di incidenza( )
αwb ed il coefficiente di momento(
CM025wb)
.A sua volta, la forza di portanza in coda
( )
Ltail viene calcolata mediante un ulteriore processo iterativo realizzato con un ciclo interno al precedente e basato sull’equazione d’equilibrio al momento definita nel precedente paragrafo 2.6, considerando come polo dei momenti il baricentro del velivolo. Da tale equazione si ricava:) 0 (ΣM =
(
)
(
) (
)
( )
(
)
(
S S S S)
wb wb eng e tail tail wb tail Xt Xa Zt H T Xa L Xa Xt Zt D M M L α α α α α sin cos cos sin cos 025 025 + − − + − − + + =In questo caso è l’angolo d’incidenza della coda ad essere iterativamente aggiornato fino alla convergenza con il medesimo margine d’errore ε dell’ordine di 0.1 %, calcolandolo come:
Condizioni di equilibrio per il velivolo rigido tail tail L S a C = α
Tale aggiornamento è conseguente al calcolo della resistenza aerodinamica dovuta alla coda, la quale dipende, oltre che dai coefficienti C e già calcolati, dal coefficiente di portanza della sola coda. Il valore d’inizio ricorsione è definito in funzione dell’angolo d’incidenza della superficie primaria, inclusi gli effetti di “downwash“ generati dal sistema ala-fusoliera sulla superficie orizzontale secondaria sperimentalmente noti in funzione del mach. In questa fase dello studio il valore di inizio ricorsione per l’angolo di calettamento della coda , ottenibile dalla seguente equazione come discusso nel paragrafo 4.9 che segue, è assunto nullo:
tail D0 Ktail s
(
wb)
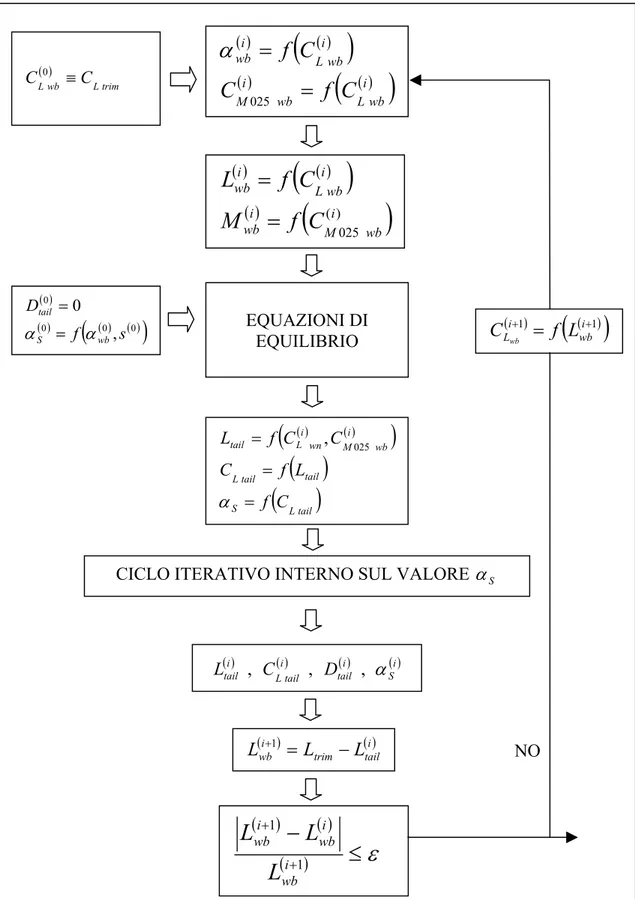
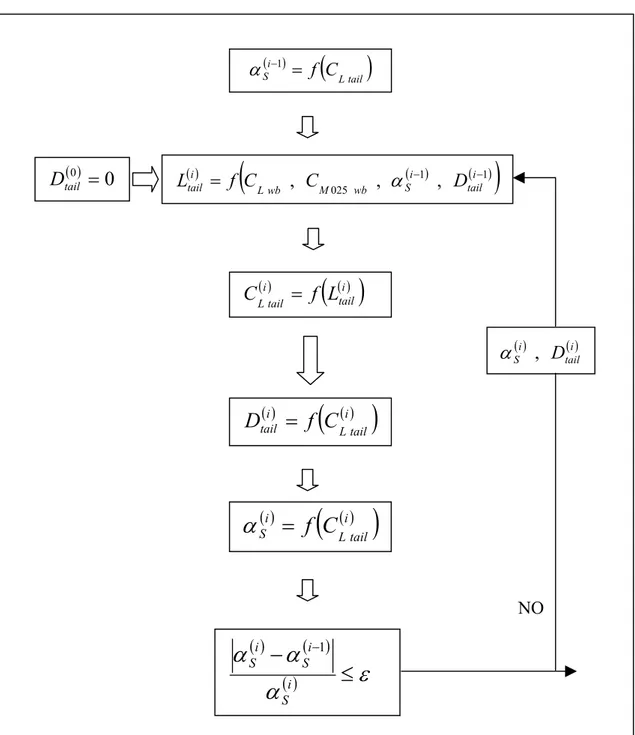
s wb S =α 1−ε −ε0 + α αNelle figure 4.11 e 4.12 sono riportati i diagrammi di flusso che descrivono il generico passo del ciclo iterativo esterno sul valore di ed interno sul valore di . In entrambi i cicli iterativi, la convergenza delle variabili è opportunamente controllata: l’iterazione ha termine solo dopo che siano stati riscontrati almeno venti valori per i quali il margine d’errore è inferiore a quello prefissato.
wb
( ) ( )0
(
( )0 ( )0)
0 , 0 s f D wb S tail α α = = ( ) ( )(
)
( )
(
Ltail)
S tail tail L i wb M wn i L tail C f L f C C C f L = = = α 025 , S α ( ) ( ) ( ) ( )i S i tail i tail L i tail C D L , , , α ( ) ( )i tail trim i wb L L L +1 = − ( ) ( ) ( )≤
ε
−
+ + 1 1 i wb i wb i wbL
L
L
( )+1 =( )
( )i+1 wb i L f L C wb NO CICLO ITERATIVO INTERNO SUL VALOREEQUAZIONI DI EQUILIBRIO ( )
( )
( ) ( )(
())
025 i wb M i wb i wb L i wbC
f
M
C
f
L
=
=
( )(
( ))
( )(
( )i)
wb L i wb M i wb L i wbC
f
C
C
f
=
=
025α
( ) trim L wb L C C 0 ≡Condizioni di equilibrio per il velivolo rigido ( )
(
)
tail L i S = f C −1 α ( )(
( )1 ( )1)
025 , , , − − = i tail i S wb M wb L i tail f C C D Lα
( )0=
0
tailD
( )( )
( )i tail i tail L f L C = ( ) ( )i tail i S , Dα
( )(
( )i)
tail L i tailf
C
D
=
( )(
( )i)
tail L i S=
f
C
α
( ) ( ) ( )ε
α
α
α
≤
−
− i S i S i S 1 NO4.8 - RISULTATI OTTENUTI.
Dal calcolo effettuato si ottengono il reale valore della forza di portanza generata rispettivamente dal sistema ala-fusoliera e dalla superficie portante posteriore, con i relativi coefficienti, l’angolo d’incidenza dell’ala e della coda, oltre ad altre grandezze da queste dipendenti tra le quali la resistenza associata alla superficie della coda orizzontale la quale generalmente per un velivolo di architettura convenzionale, ed in particolare per uno con “coda a T“, comporta degli effetti che possono non risultare trascurabili.
Le equazioni utilizzate in quest’analisi sono esplicitate in funzione del rapporto W/δ . Per ogni condizione di volo identificata da un numero di mach costante tale rapporto è fatto variare tra un valore minimo di 10000 Lb, uguale per tutti i numeri di mach, ed un valore massimo che aumenta di volta in volta, andando a studiare condizioni di volo a mach superiori, come riportato in tabella 4.7.
M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 ] [Lb W MAX δ 85000 385000 490000 600000 665000 ] [ min Lb W δ 10000
Tab. 4.7: Valori massimi significativi del parametro
δ
W
.
Per valori di W/δ superiori a quelli indicati in tabella 4.7 riferiti ai distinti valori del numero mach non è possibile individuare per la macchina configurazioni di volo equilibrato perché non compatibili con la massima portanza della superficie alare. Il fine di far variare il parametro W /δ entro un opportuno intervallo di valori è valutare le condizioni limite fino alle quali è garantito l’equilibrio del velivolo. In questo modo analizzando tutte le possibili condizioni di volo equilibrato in cui può trovarsi la macchina, come detto ci si arresta quando sono prese in considerazione quelle condizioni in cui si sfrutta la massima capacità portante possibile dell’ala.
Condizioni di equilibrio per il velivolo rigido Nelle figure 4.13 - 4.27 sono rappresentate, per le diverse posizioni del baricentro e per i valori del mach esaminati, le curve “equilibrate” CLtail = f
(
W/δ)
, CDtail = f(
W/δ)
oltre alle curve del coefficiente di portanza del velivolo e del coefficiente di momento del sistema ala-fusolieraL
C
(
CM 025)
wb in funzione dell’angolo d’incidenza.Infine nelle figure 4.28 – 4.32 sono proposti alcuni grafici riassuntivi relativi agli andamenti del coefficiente di portanza e di resistenza della superficie portante posteriore oltre agli andamenti del coefficiente di portanza del velivolo e del coefficiente di momento del sistema ala-fusoliera per fissate posizioni del baricentro del velivolo al variare del numero di mach di volo.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.14: Curva “equilibrata“ del coefficiente di portanza del velivolo per M = 0.20.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.17: Curva “equilibrata“ del coefficiente di portanza del velivolo per M = 0.50.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.20: Curva “equilibrata“ del coefficiente di portanza del velivolo per M = 0.60.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.23: Curva “equilibrata“ del coefficiente di portanza del velivolo per M = 0.70.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.26: Curva “equilibrata“ del coefficiente di portanza del velivolo per M = 0.75.
Fig. 4.27: Curva “equilibrata“ del coefficiente
(
)
wb MFig. 4.28: Andamento del in funzione dell’angolo d’incidenza della superficie orizzontale di coda per le tre posizioni del baricentro e per i mach esaminati.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.29: Andamento del
(
in funzione dell’angolo d’incidenza della superficie orizzontale di coda per le tre posizioni del baricentro e per i mach esaminati.)
tailD C
Fig. 4.30: Andamento del
(
CL)
tail in funzione del( )
CD tail per le tre posizioni del baricentro e per i mach esaminati.Condizioni di equilibrio per il velivolo rigido
Fig. 4.31: Andamento del C velivolo in funzione dell’angolo d’incidenza dell’ala per le tre posizioni del baricentro e per i mach esaminati. L
Fig. 4.32: Andamento del
(
)
wb MC 025 in funzione dell’angolo d’incidenza in ala per i diversi mach esaminati.
4.9 - ANGOLO DI CALETTAMENTO DELLA CODA.
Determinate le condizioni d’equilibrio del velivolo, essendo noti sia l’angolo di incidenza dell’ala che della coda orizzontale, è possibile valutare l’angolo di calettamento della superficie portante posteriore mediante la seguente relazione: s
(
)
(
α
1
ε
ε
0)
α
−
−
α−
=
S wb wbs
In particolare tale dato riguarda le caratteristiche meccaniche di funzionamento della coda, importanti per l’azione di comando che il pilota del velivolo deve svolgere quando effettua le manovre.
Nelle figure 4.33 – 4.37 sono riportati gli andamenti dell’angolo di calettamento della coda orizzontale in funzione del parametro W /δ per le tre distinte posizioni del baricentro del velivolo nelle condizioni di volo prese in esame.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.33: Andamento dell’angolo di calettamento della coda orizzontale in funzione del parametro W/δ per condizioni di volo a mach 0.20.
Fig. 4.34: Andamento dell’angolo di calettamento della coda orizzontale in funzione del parametro W/δ per condizioni di volo a mach 0.50.
Fig. 4.35: Andamento dell’angolo di calettamento della coda orizzontale in funzione del parametro W/δ per condizioni di volo a mach 0.60.
Fig. 4.36: Andamento dell’angolo di calettamento della coda orizzontale in funzione del parametro W/δ per condizioni di volo a mach 0.70.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.37: Andamento dell’angolo di calettamento della coda orizzontale in funzione del parametro W/δ per condizioni di volo a mach 0.75.
4.10 - INVILUPPO DI VOLO.
La ricostruzione delle curve “equilibrate“ del coefficiente di portanza del velivolo in funzione dell’angolo d’incidenza dell’ala per tre distinte posizioni del centro di gravità della macchina e per valori del mach pari a: 0.20. 0.50, 0.60, 0.70, 0.75, consente di individuare i massimi valori del coefficiente di portanza del velivolo in volo equilibrato nelle diverse condizioni operative analizzate. Tali valori sono riportati nella tabella 4.8 seguente e nella figura 4.38 viene rappresentato l’andamento del C con il mach di volo per le tre posizioni del baricentro. La conoscenza dei massimi valori possibili per il nelle condizioni di volo corrispondenti ai mach esaminati consente di ricostruire mediante interpolazione la curva di stallo, ovvero la curva limite superiore, dell’inviluppo di volo. Infatti, imponendo l’uguaglianza della portanza e del peso del velivolo si identifica la massima quota raggiungibile per ogni valore del C e per il mach ad esso corrispondente. Al fine di valutare le condizioni di volo limite maggiormente vincolanti si considera il massimo peso possibile per il velivolo corrispondente al peso massimo al
MAX L C MAX L C MAX L MAX L
decollo di 77700 Lb. In questo modo sono definite distinte copie di valori: quota, mach di volo
(
H ,M)
, per ogni C precedentemente determinato.)
MAX L
MAX
L’interpolazione sul piano dei punti corrispondenti a tali coppie consente di tracciare la curva continua limite superiore dell’inviluppo, riportata nella figura 4.39 che segue.
(
H ,M M = 0.20 M = 0.50 M = 0.60 M = 0.70 M = 0.75 CG at 0.15% m.a.c. 1.464 1.049 0.915 0.837 0.812 CG at 0.25% m.a.c. 1.410 1.024 0.903 0.828 0.801 L C CG at 0.45% m.a.c. 1.359 1.003 0.886 0.814 0.786Tab. 4.8: Valori massimi raggiungibili dal coefficiente di portanza a differenti mach.
Condizioni di equilibrio per il velivolo rigido
Fig. 4.39: Inviluppo di volo: quota – mach di volo.
La curva a massima portanza completa la rappresentazione grafica dell’inviluppo di volo del velivolo, parzialmente ricostruito in precedenza nel paragrafo 4.4. Tale diagramma è limitato superiormente da una retta orizzontale, corrispondente ad una quota di volo che il velivolo non può mai oltrepassare. Tale quota, compatibilmente con quanto riportato nel manuale di volo, è pari a 48800 Ft.
Nella figura 4.40 sono rappresentati gli andamenti della velocità equivalente di progetto per la crociera V e di affondata V per il velivolo in funzione della quota di volo. Questi sono ottenuti mediante interpolazione di valori sperimentali riportati nel manuale di volo del velivolo e contrassegnati in figura con il simbolo circolare.
C D
4.11 - DIAGRAMMI DI MANOVRA DEL VELIVOLO RIGIDO.
La valutazione delle condizioni operative critiche per il velivolo dal punto di vista dei carichi agenti sulla struttura richiede la costruzione dei diagrammi di manovra, in base a quanto specificato nella normativa FAR 25.1501. Secondo la normativa FAR 25.333 i requisiti relativi alla resistenza strutturale del velivolo devono essere rispettati per ogni possibile combinazione di velocità equivalente – fattore di carico a cui il velivolo può operare: tutte le possibili combinazioni sono quelle individuate da tutti i punti delimitati dal diagramma di manovra relativo ad una generica condizione di volo definita in termini di peso, quota e posizione del baricentro del velivolo.
La costruzione del diagramma di manovra relativo ad una fissata condizione necessita della valutazione di velocità caratteristiche definite nel paragrafo 335 della normativa FAR 25. Sono riassunte di seguito le velocità equivalenti fondamentali per l’analisi dei carichi agenti sul velivolo in condizioni di flaps retratti ed in assenza di raffica.
1. Velocità di stallo con flaps retratti V : è la minima velocità equivalente che consente il sostentamento del velivolo al massimo valore del coefficiente di forza normale complessivo per il velivolo . Questo coefficiente può essere assunto con ottima approssimazione coincidente con il massimo coefficiente di portanza del velivolo C .
1 S
CN MAX
MAX L
Condizioni di equilibrio per il velivolo rigido 2. Velocità di progetto per la crociera V : secondo la normativa FAR 25.335 (a) il
massimo valore per questa velocità deve risultare sufficientemente maggiore della velocità di progetto per la massima intensità di raffica, ma non può in ogni caso superare la massima velocità in volo livellato alla massima spinta continuativa per la quota considerata. Per le quote in cui la velocità in affondata V è limitata dal numero di mach la V può essere limitata ad un numero di mach prefissato.
C
D C
3. Velocità di progetto per la manovra V : secondo la FAR 25.335 (c) (1) (i) (ii) questa deve risultare non inferiore al prodotto
A
n
S1
V , essendo V la velocità di stallo precedentemente indicata e n il valore limite positivo del fattore di carico da manovra valutato a V ; contemporaneamente non può essere superiore sia alla V sia alla velocità in corrispondenza della quale la curva relativa al C raggiunge il valore limite positivo del fattore di carico, qualunque delle due sia la minore. Infine la V deve essere valutata per ogni condizione operativa in termini di peso e quota cui può trovarsi il velivolo.
1 S N C C MAX A
4. Velocità di progetto in affondata V : la FAR 25.335 (b) (2) impone che questa sia scelta in modo che il rapporto V non sia maggiore di 0 ovvero che il margine tra il rapporto V V non sia inferiore a in alcun caso. D M / C / e C C M D D M V / 8 . 05 . 0 C D/MD M
Facendo riferimento alla normativa citata e quindi alle definizioni sopra riportate, si sceglie di costruire i diagrammi di manovra del velivolo di riferimento relativi a 27 possibili condizioni operative in cui questo può trovarsi: tali condizioni sono riferite a tre distinti valori del peso, della quota e della posizione del baricentro del velivolo. In riferimento a quanto esposto nel precedente paragrafo 4.10, per la costruzione della curva relativa al si tiene conto della variazione del massimo coefficiente di portanza del velivolo al variare del numero di mach di volo per effetto della comprimibilità del flusso.
MAX N C
Per la scelta delle condizioni operative da analizzare è necessaria preliminarmente una stima del peso del velivolo in diverse possibili configurazioni tipiche e rappresentative
delle reali condizioni d’impiego per la macchina. In base ai riferimenti [10] e [13] si assumono i seguenti valori:
• Peso a vuoto operativo
( )
Weo corrispondente alla configurazione velivolo con carico pagante e carburante non imbarcati: 48500 Lb.• Peso massimo in assenza di carburante
(
WMZF)
corrispondente alla configurazione velivolo con massimo carico pagante imbarcabile e privo di carburante: 66400 Lb. • Peso massimo al decollo(
WTO)
corrispondente alla configurazione velivolo concarico pagante e carburante imbarcati in proporzioni tali da raggiungere il limite massimo consentito: 77700 Lb.
Le quote che vengono prese in considerazione sono 0 Ft, 20000Ft, 30000 Ft, mentre per le posizioni del baricentro del velivolo si assume che possa trovarsi in corrispondenza rispettivamente del 15 %, 25 % e 45 % della corda media aerodinamica dell’ala.
Si fa notare che per le velocità equivalenti V e V necessarie per la costruzione dei suddetti diagrammi si adottano i valori indicati sul manuale di volo del velivolo i cui andamenti con la quota sono stati rappresentati in forma grafica in figura 4.40. In modo analogo viene selezionata la velocità equivalente V , ovvero la massima a cui è possibile per il pilota estrarre i flaps. La velocità equivalente V è valutata come la minima velocità alla quale si raggiunge il valore limite negativo del fattore di carico pari a -1.
C D
H F
Nelle figure 4.41 – 4.43 che seguono sono riportati alcuni diagrammi di manovra relativi alle condizioni operative che risultano importanti per l’identificazione dell’inviluppo di carico della superficie orizzontale di coda. Gli andamenti delle curve relative al massimo valore del coefficiente di forza normale corrette per gli effetti della comprimibilità del flusso, opportunamente contraddistinte nelle figure, mostrano come tali effetti aumentino fondamentalmente all’aumentare della quota operativa.
Condizioni di equilibrio per il velivolo rigido
Condizioni di equilibrio per il velivolo rigido
4.12 - CONDIZIONI DI TRIM PER VOLO LIVELLATO CON FATTORE DI CARICO UNITARIO ALLE VELOCITÀ VA e VD.
I diagrammi di manovra consentono di identificare per ogni condizione operativa analizzata i valori delle velocità equivalenti V e V , cui corrispondono distinti mach, in corrispondenza delle quali è richiesto di analizzare lo stato di sollecitazione del velivolo al fine di valutare i massimi carichi agenti sulla coda orizzontale. Tale valutazione richiede di determinare preliminarmente le condizioni di trim per volo livellato a fattore di carico unitario in corrispondenza della V e V : successivamente, partendo da tali condizioni d’equilibrio si studia il comportamento dinamico del velivolo al fine di svolgere un’analisi dei carichi seguendo le esplicite richieste dei regolamenti aeronautici relative alla resistenza strutturale del velivolo.
A D
A D
Le forze di portanza agenti sull’ala e sulla coda del velivolo nelle condizioni di trim, come anche i relativi coefficienti e tutte le grandezze fisiche che caratterizzano il sistema, vengono calcolati mediante la medesima procedura illustrata nei precedenti paragrafi 4.6 e 4.7. Si fa notare che in questo caso, avendo fissato a priori i valori del peso e della quota operativi per il velivolo, non è necessario elaborare le equazioni d’equilibrio riconducendosi al parametro di studio W /δ rappresentativo di tutte le possibili condizioni di volo in termini di peso e quota.
Nella tabella 4.9 che segue sono indicati i valori delle sollecitazioni agenti sulla coda orizzontale
(
L ,tail MtailA
)
insieme con altre grandezze di particolare interesse nelle condizioni di trim analizzate alla V e V a partire dalle quali si registrano le massime sollecitazioni per la coda in conseguenza delle manovre simulate. In particolare si tratta di condizioni di volo al massimo peso al decollo per il velivolo a livello del mare per una velocità equivalente V cui corrisponde un mach di 0.31 e per una velocità equivalente Vcui corrisponde un mach pari a 0.65.
A D
Condizioni di equilibrio per il velivolo rigido CONDIZIONE DI VOLO M = 0.31 H = 0 [Ft] CONDIZIONE DI VOLO M = 0.65 H = 0 [Ft] PESO [Lb] W = 777000 PESO [Lb] W = 77700 e T [Lb] 5.42⋅103 14.12⋅103 L C 0.534 0.124 D C 0.0357 0.0225 C.G. [%m.a.c.] C.G. [%m.a.c.] 0.15% 0.45% 0.15% Lwb C 0.613 0.526 0.157 Lt C −0.131 0.023 −0.099 w α [deg] 4.98 4.01 −0.16 S α [deg] −2.14 0.37 −1.39 wb L [Lb] 13.24⋅104 7.46⋅104 12.18⋅104 t L [Lb] −5.67⋅104 1.09⋅103 −4.92⋅104 t D [Lb] 2.64⋅102 2.21⋅102 9.53⋅102 t M [LbFt] 2.32⋅106 −2.95⋅104 2.01⋅106
Tab. 4.9: Valori di trim delle diverse grandezze relativi alle condizioni di volo indicate nell’ipotesi di velivolo rigido.