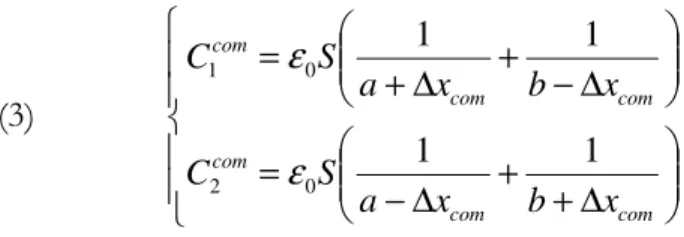PARTE PRIMA: I Concetti Base
PARTE PRIMA: I Concetti Base
PARTE PRIMA: I Concetti Base
PARTE PRIMA: I Concetti Base
In questa prima parte introduttiva verranno presentati gli elementi basilari e necessari alla comprensione del successivo svolgimento della Tesi. L’obiettivo di questa parte della Tesi è quello di presentare le linee essenziali dell’esperimento GGG ed i primi elementi di Dinamica dei Rotori (per presentare la nomenclatura ed i fenomeni base che verranno poi studiati in modo più specifico nelle parti successive della Tesi). Alcuni di questi elementi sono superflui per la fruizione della seconda parte della Tesi (ad esempio la spiegazione dettagliata degli elementi costitutivi di GGG oppure il comportamento di un rotore in presenza di una anisotropia della costante elastica) tuttavia essi diventano indispensabili per la terza parte della tesi in cui viene analizzata una simulazione realistica per il controllo dei moti di whirl in GGG. Ho pensato allora che fosse inutile presentare gli argomenti a varie riprese con il rischio di ripetere più volte lo stesso concetto e fosse meglio –ai fini espositivi- dare una certa forma di continuità presentando subito in una sezione a parte tutti gli elementi che sarebbero poi stati necessari alla comprensione dell’intera tesi nel suo insieme. Nella presente parte della Tesi si presuppone comunque che il lettore sia informato sul significato del Principio di Equivalenza, sulla sua importanza nell’ambito della Teoria della Relatività Generale ed eventualmente su alcuni esperimenti terrestri classici implementati per la sua verifica. Per una review aggiornata sul Principio di Equivalenza ed il suo confronto con gli esperimenti è possibile consultare [1]-[3] della bibliografia.
I. L’esperimento GG e GGG (GG on the Ground)
I. L’esperimento GG e GGG (GG on the Ground)
I. L’esperimento GG e GGG (GG on the Ground)
I. L’esperimento GG e GGG (GG on the Ground)
1. I Principii basilari di GG 1. I Principii basilari di GG 1. I Principii basilari di GG 1. I Principii basilari di GG
L’esperimento GG è un un esperimento spaziale progettato presso l’Università di Pisa verso gli inizi degli anni ’90 ([4]-[8]) con lo scopo di verificare il Principio di Equivalenza Debole mediante una verifica diretta del principio universale di caduta libera.
Storicamente i progetti spaziali per la verifica diretta del Principio di Equivalenza Debole, nascono nel 1970 con Chapman e Hanson [9] i quali proposero di ripetere l’esperimento del Barone Von Eötvös in un laboratorio in orbita bassa intorno alla Terra. Il progetto da loro proposto (e che permette di capire il concetto base di GG) era quello di misurare la violazione del Principio di Equivalenza Debole grazie all’uso di due cilindri coassiali di uguale massa, ma di differente composizione atomica. Supponendo, infatti, che la massa gravitazionale sia dipendente dalla composizione dei corpi e dunque sia diversa dalla massa inerziale, dati due corpi cilindrici coassiali A e B di uguale massa inerziale ma di diversa composizione, le equazioni del moto per i due corpi in orbita attorno alla Terra sono date da:
(1) Φ ∇ − = Φ ∇ − = ⊕ ⊕ B g B B i A g A A i m a m m a m
dove, chiamando h l’altezza orbitale, il potenziale gravitazionale altro non è che:
(2) h R GM + = Φ ⊕ ⊕ ⊕
Da queste equazioni si ricava immediatamente che un eventuale segnale di violazione del Principio di Equivalenza (una diversa reazione dei corpi rispetto al potenziale gravitazionale) sarebbe dato da
(3) ⊕ ⊕ ⊕ ⊕ Φ ∇ − = Φ ∇ − − = ⇒ Φ ∇ − = Φ ∇ − =
η
B i B g A i A g PE B i B g B A i A g A m m m m a m m a m m aDove il parametro η rappresenta il parametro Eötvös che è il parametro adimensionale che viene misurato in questo genere di verifiche sperimentali [1] definito come (4) B i g A i g B i g A i g B i g A i g m m m m m m m m m m m m − ≈ + − = 2 1 η
In questo contesto sperimentale, dunque, il segnale di violazione del Principio di Equivalenza si risolverebbe in un’accelerazione differenziale fra le due masse che deve poter essere misurata nello spazio. Il valore che vogliamo raggiungere nella precisione su η in questo contesto si traduce automaticamente in una prima stima sull’accelerazione che dovremo essere in grado di misurare.
Agli inizi degli anni ‘70, un progetto che si basasse su queste considerazioni fondamentali fu concepito a Stanford da Worden e Everitt che diedero vita al progetto STEP (Satellite Test of Equivalence Principle)[10-11]. Tale progetto si propone di ottenere una precisione su η di circa 10-18. Sostanzialmente in questo
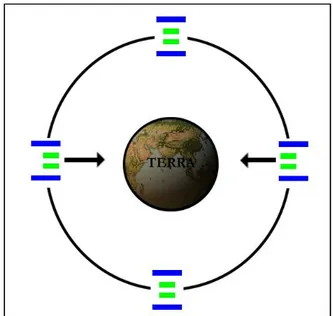
progetto vengono utilizzate due masse test coassiali di forma cilindrica, il loro asse di simmetria giace sul piano orbitale del satellite e su tale piano viene dunque rivelato il segnale di un’eventuale violazione. Se uno dei due cilindri fosse attratto dalla Terra più dell’altro –il che corrisponderebbe ad una eventuale violazione del Principio di Equivalenza- avverrebbe un movimento relativo tra i due cilindri. Tale
effetto sarebbe massimo quando l’asse di simmetria è rivolto verso il centro della Terra e nullo quando è perpendicolare alla direzione satellite-Terra come mostrato in figura.
fig I.1: violazione del principio di equivalenza in STEP
Una violazione del Principio di Equivalenza produrrebbe, allora, un segnale di intensità variabile con frequenza pari alla frequenza orbitale del satellite (che ha un periodo, in orbita bassa attorno alla Terra, di circa 6000 sec).
Pur essendo tale progetto, nelle sue linee essenziali, molto semplice, l’aver scelto di rilevare il segnale lungo l’asse di simmetria dei cilindri, fa sì che sia presente un rumore che compete direttamente con il segnale. In condizioni di bassa pressione, infatti, un cilindro, le cui facce siano a temperature diverse, è soggetto ad una accelerazione lungo l’asse di simmetria e, se la pressione residua del gas non è notevolmente bassa, il valore assunto da questa accelerazione può essere anche molto grande. Questo effetto si chiama effetto radiometrico e per eliminare questo disturbo gli ideatori di STEP hanno scelto di lavorare in ambiente criogenico, utilizzando elio superfluido. Tuttavia, la grande quantità di elio prevista per operare a bassa temperatura (cioè alcune centinaia di litri) può causare altre perturbazioni sull’esperimento e questo è un problema che ancora è in fase di studio. Infatti, malgrado i numerosi progetti presentati (Worden e Everitt, 1973; Worden, 1976; Worden, 1987; Blaser et al., 1993; Blaser et al., 1996), il satellite STEP non ha superato la selezione per lo studio di fase B, ed è attualmente in progetto una variante di minor costo e dimensioni, MiniSTEP.
In questo contesto teorico e sperimentale si inserisce GG, l’esperimento che tatteremo diffusamente nell’ambito della nostra tesi, il quale si propone di ottenere una verifica del Principio di Equivalenza con una precisione di una parte su 1017.
fase di progettazione sono state operate diverse scelte innovative che distinguono radicalmente GG da tutti i progetti ad esso concorrenti.
A differenza di STEP, in GG il segnale non viene rilevato alla frequenza orbitale, ma viene modulato dalla frequenza di rotazione dell’intero satellite (2 Hz). Questa rotazione attorno all’asse di massimo momento di inerzia che è anche l’asse di simmetria del satellite, oltre che modulare il segnale di violazione, permette automaticamente di stabilizzare il satellite.
La rotazione attorno l’asse di simmetria dei cilindri e la scelta di misurare il segnale di violazione nel piano ortogonale ad esso, permette di eliminare l’effetto radiometrico che richiedeva a STEP, per essere eliminato, di compiere il proprio esperimento all’interno di un ambiente criogenico con grosse quantità di elio superfluido. In questo paragrafo analizzeremo rapidamente gli elementi generali del progetto spaziale per poi vedere più nel dettaglio le soluzioni tecniche e le stime quantitative applicate nella sua realizzazione terrestre che è poi il vero soggetto della nostra tesi.
a. Elementi general a. Elementi general a. Elementi general
a. Elementi generali del satellitei del satellitei del satellitei del satellite
L’orbita scelta per il satellite GG è a 520 km e con inclinazione prossima allo zero. La scelta dell’altezza di 520 km è una mediazione fra due necessità opposte:
1. l’eliminazione del drag atmosferico – che diventa comparabile con la pressione di radiazione solare ad un’altezza di 640 Km
2. l’intensità del segnale che dipendendo dal potenziale gravitazionale terrestre è tanto maggiore quanto più l’orbita è bassa.
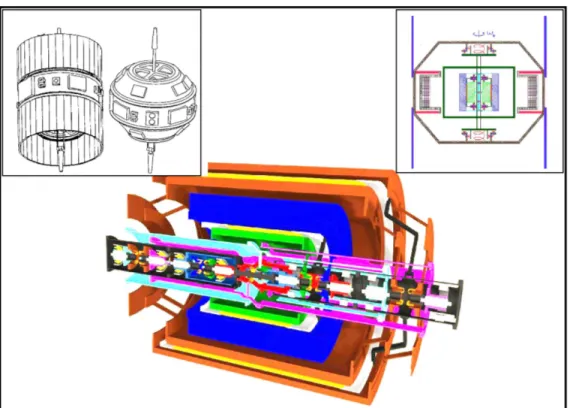
La mediazione fra queste due necessità ha portato alla scelta di 520 km per l’altezza dell’orbita. Per quanto riguarda l’inclinazione, invece, per l’esperimento è stata scelta un’orbita equatoriale che ha l’indubbio vantaggio di non dover richiedere correzioni del satellite a causa della precessione dei nodi che a quelle latitudini non avvengono al primo ordine di approssimazione. Come controparte della medaglia, tuttavia, il satellite sarebbe è più soggetto agli sbalzi termici, dovendo attraversare il cono d’ombra della terra ed essendo così soggetto ad un effetto perturbativo solo parzialmente eliminabile con un rivestimento termico e la rotazione veloce. Il piano sul quale viene rilevato il segnale di violazione è chiaramente il piano orbitale, per cui il satellite viene posto in rotazione attorno all’asse normale a questo piano. Come detto la rotazione avviene ad una frequenza di 2Hz cioè ad una frequenza molto più alta rispetto a tutti gli altri progetti. Il satellite è stato disegnato per contenere quattro cilindri concentrici dalla massa inerziale di 10 kg ciascuno, due di essi costituiscono le masse test sorgenti del segnale di violazione, mentre gli altri due –identici per materiale e massa- costituiscono un sanity check per rigettare eventuali falsi segnali. Quella di supportare –oltre alle masse proprie per il test- una coppia di masse di controllo è una particolarità di GG che lo distingue dagli altri progetti similari.
fig I.2: Il satellite GG
Le varie masse sono sospese in un laboratorio chiamato PGB (Pico Gravity Box) che ha il duplice vantaggio di ridurre il rumore vibrazionale del satellite e di eleminare il pericolo di perturbazioni elettrostatiche. Infatti la PGB è sospesa allo spacecraft a mezzo di molle elicoidali di bassa costante elastica, questo permette di attuare un naturale filtraggio di tutti quei rumori vibrazionali di frequenza maggiore alla frequenza naturale di oscillazione e contemporaneamente permette di scaricare a terra le cariche elettrostatiche delle masse. Le perturbazioni elettrostatiche, infatti, costituiscono uno dei maggiori problemi in questo genere di esperimenti perchè la presenza anche di piccole cariche elettriche sulle masse può portare a segnali molto più forti del segnale da misurare.
b.La rilevazione del segnale b.La rilevazione del segnale b.La rilevazione del segnale b.La rilevazione del segnale
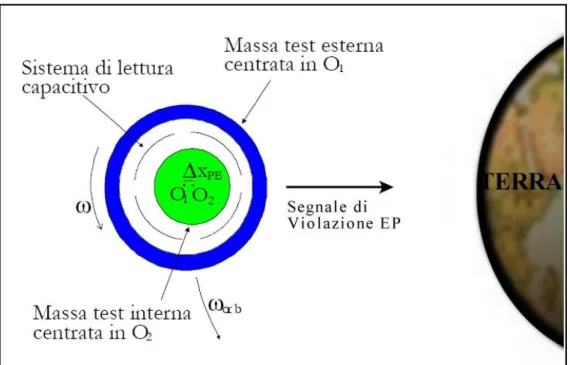
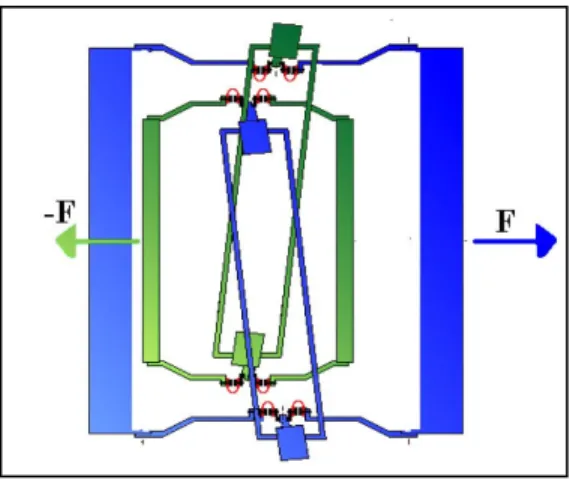
Le due masse test (ed equivalentemente le due masse di controllo) sono accopiate fra di loro con dei giunti cardanici particolari –che analizzeremo più nel dettaglio in seguito- dotati di una bassissima costante elastica e che permettono alle masse di muoversi liberamente sul piano del segnale. Sotto l’azione di una forza esterna (eventualmente dovuta alla violazione del Principio di Equivalenze) le masse si separano fra di loro generando dunque uno spostamento differenziale.
fig I.3: Spostamento differenziale delle masse test di GG
Dalla formula aPE =−
η
∇Φ⊕ si ottiene subito che per misurare η con unaprecisione di 10-17 è necessario poter rilevare un’accelerazione che agisce sulle
masse test che è 15 2
sec / 10 4 . 8 cm aPE − ⋅
≅ , lo spostamento relativo fra i due
cilindri è dunque x a cm d PE PE 11 2 6.3 10 − ⋅ ≅ = ∆
ω
.Per rilevare uno spostamento di questa entità, sono state inserite fra le due masse test quattro piastre capacitive, in grado così di rilevare la differenza di capacità dovuta ad uno spostamento relativo fra i cilindri. Un sistema di lettura capacitivo di tal sorta permette, come vedremo, di discriminare fra spostamenti comuni operati dalle due masse e spostamenti differenziali reagendo in modo distinto.
fig I.4: violazione del principio di equivalenza in GG
c. La rotazione supercritica c. La rotazione supercritica c. La rotazione supercritica c. La rotazione supercritica
Oltre a ridurre i rumori meccanici ed elettrici, la rotazione veloce delle masse accoppiate rispetto a tutti gli altri progetti ha un altro indiscutibile vantaggio che deriva direttamente dalla dinamica dei rotori. Il fenomeno è chiamato autocentratura in rotazione supercritica ed è un fenomeno che avviene quando due rotori debolmente accoppiati entrano in rotazione ad una frequenza maggiore della frequenza di risonanza del sistema. In queste condizioni i due rotori tendono ad eliminare la distanza iniziale ε fra i due centri di massa e si assestano ad una distanza relativa rg che è circa
(5) 0 ≅0 − ≅
ε
ω
ω
s g rQuesto effetto, che avremo modo di analizzare in seguito, è di capitale importanza perchè permette di ridurre l’offset iniziale che incorre nel posizionamento dei cilindri e che può essere alquanto fastidioso da discriminare dal segnale di violazione. L’esperimento in questione, infatti, è un esperimento che mira a rilevare un’accelerazione differenziale fra le due masse test. Questa accelerazione differenziale deve essere il risultato di un diverso accoppiamento fra un’uguale azione gravitazionale e due masse di diversa composizione. Per rilevare il diverso accoppiamento è necessario che la forza in questione sia esattamente la stessa,
Nel caso di GG e di GGG, la precisione nell’auto-centratura dei rotori raggiunge 10-10 m partendo da un offset iniziale di 10-5.
Ho ritenuto importante illustrare brevemente i concetti base che hanno ispirato l’ideazione di GG, prima di analizzare a fondo la costituzione di GGG, in quanto questo altro non è che la sua implementazione terrestre al fine di verificare la fattibilità di GG e molte soluzioni possono essere comprese solo tenendo di conto della sua successiva implementazione spaziale.
fig I.5: elementi costitutivi di GGG
2. Descrizione sommaria degl 2. Descrizione sommaria degl 2. Descrizione sommaria degl
2. Descrizione sommaria degliiii elementi costituivi di GGG elementi costituivi di GGG elementi costituivi di GGG elementi costituivi di GGG
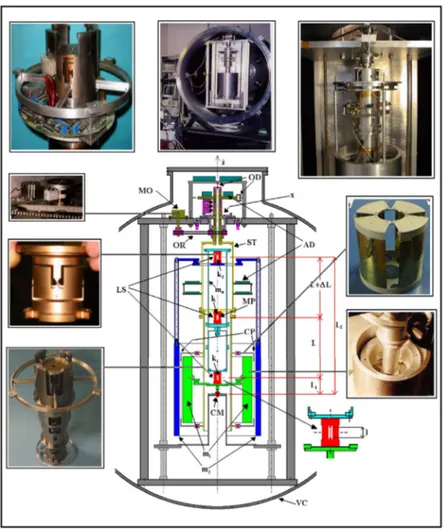
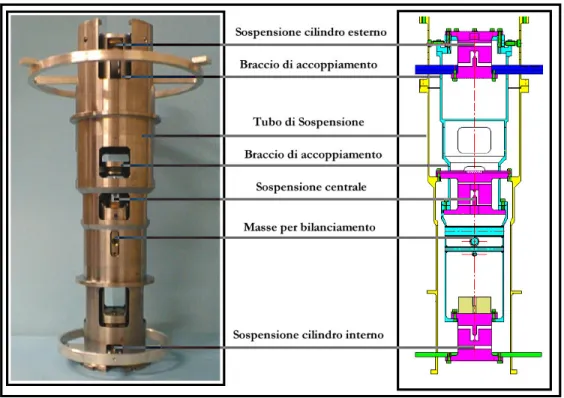
Avendo già analizzato brevemente l’idea ispiratrice di GG, in questo capitolo possiamo descrivere più dettagliatamente la realizzazione meccanica di GGG che consiste nell’adattamento terrestre di GG per la verifica della sua fattibilità. In GGG, come d’altronde in GG, l’accelerazione differenziale viene misurata da due cilindri test coassiali accoppiati fra di loro da un braccio bilanciato sospeso al centro che forma una bilancia verticale a braccia uguali., il tutto posto dentro una camera a vuoto. Lo schema dell’apparato è riportato in figura I.6.
Lo schema rappresenta una sezione verticale dell’apparato visualizzato nella camera a vuoto VC.
A differenza del progetto spaziale in cui la rotazione è assicurata dalla rotazione dell’intero satellite, per GGG è necessario l’utilizzo di un motore MO che trasmetta la rotazione al tubo di sospensione ST mediante una catena OR fatta di anelli di plastica. Dentro il tubo di sospensione disegnato in giallo si trova il braccio di accoppiamento delle due masse disegnato in azzurro. Il braccio di accoppiamento pesa ma=0.3 Kg
ed è lungo 2L+∆L= ca. 0.38 m. Esso è sospeso nel suo punto di mezzo MP grazie ad una sospensione laminare LS di costante elastica k=ca. 10-3 J/m2
e lunghezza l=5 10-3 m.
Il centro di massa del braccio è spostato rispetto al centro di sospensione MP di una distanza
∆L/2. La quantità ∆L può essere fig I.6: schema meccanico di GGG
aggiustata di modo da essere leggermente positiva o leggermente negativa grazie ad un piccolo anello posto nella metà inferiore del braccio.
Il cilindro interno di massa m1= 10 kg, è disegnato di colore verde ed è sospeso al
braccio inferiore della bilancia a mezzo della sospensione k1 del tutto identica alla
sospensione laminare k. Il punto di sospensione del cilindro dista dal suo centro di massa di una lunghezza L1, mentre il cilindro esterno, colorato di blu e di massa
m2=10 kg, è sospeso a mezzo della sospensione k2 a distanza L2 dal suo centro di
massa.
Le sospensioni laminari sono identiche fra loro: k1=k2=k e sono di una
composizione metallica (CuBe) che assicura lo scaricamento a terra di cariche elettrostatiche. Queste sospensioni sono appositamente disegnate per avere una a forte costante elatica nei confronti di movimenti diretti lungo l’asse verticale ed avere invece una costante elastica molto debole nei confronti di ogni movimento sul piano orizzontale. Le immagini rappresentano le foto delle sospensioni: quella in basso rappresenta una prima versione delle sospensioni, mentre quella a destra il nuovo tipo usato per l’esperimento. Esse sono direttamente ricavate da una barra di CuBe per assicurare un alto fattore di qualità.
fig I.7: sospensioni laminari di GGG
Queste sospensioni sono composte da quattro fogli di spessore 70 µm, due di essi giacciono sul piano x-z e assicurano movimenti lungo l’asse y mentre gli altri due giacciono sul piano y-z e assicurano il movimento lungo l’asse delle x.
La figura sottoriportata rappresenta il tubo di sospensione ed il braccio di accoppiamento uno dentro l’altro.
fig I.8: tubo di sospensione di GGG
Infine un ammortizzatore passivo non rotante è posto all’estremità inferiore dell’ultima sospensione laminare al fine di ammortizzare le oscillazioni che potrebbero incorrere nel passaggio del rotore attraverso la frequenza di risonanza (velocità angolare critica) e le regioni di instabilità (vedi cap. II). Una volta superate queste velocità l’ammortizzatore passivo può essere disconesso e al suo posto può essere inserito un ammortizzatore attivo più raffinato.
3. Risposta a Forze Comuni e Differenziali 3. Risposta a Forze Comuni e Differenziali 3. Risposta a Forze Comuni e Differenziali 3. Risposta a Forze Comuni e Differenziali
Per comprendere il funzionamento basilare dell’accelerometro differenziale introduciamo un modello molto semplificato del suo apparato, quello che viene chiamato modello minimo e che verrà poi corretto e ampliato in seguito.
Il modello minimo qui
rappresentato permette di stabilire il periodo di oscillazione naturale delll’accelerometro, il quale –come vedremo in seguito- risulta essere per piccole oscillazioni
2 2 2 1 2 2 ) ( 3 2 L L g L m m kl Td ∆ − + =
π
dove g rappresenta la gravità locale che può essere sia positiva che negativa. Dall’equazione del periodo naturale di oscillazione, risulta chiaramente che l’azione della gravità può essere ambivalente a seconda della quantità ∆L. Se ∆L è positivo, formalmente la gravità agisce come una molla positiva, incrementando l’accoppiamento fra le masse, se è negativo agisce invece come una molla negativa.
Il periodo di oscillazione naturale è quantomeno importante perchè è direttamente implicato nella rilevazione del segnale. Infatti più è lungo il periodo di oscillazione naturale maggiore sarà lo spostamento fra i centri di massa e dunque il segnale rilevato da un’accelerazione differenziale.
fig I.9: comportamento dell’accelerometro differenziale sotto l’azione di forze comuni e differenziali In effetti l’apparato reagisce sotto l’azione di una forza differenziale costante allontanando i centri di massa fra di loro e inclinando l’angolo rispetto all’asse z secondo la legge (1) m F T x x x d diff 2 2 1 2 4
π
= − = ∆Facendo risultare così una dipendenza quadratica dal periodo di oscillazione naturale. In linea teorica l’apparato dovrebbe rimanere inalterato sotto l’azione di una forza comune. Nella pratica un qualsiasi strumento reale non può essere totalmente differenziale, in questo caso è evidente che la presenza di ∆L rende l’apparato sensibile anche a forze comuni e chiamando dunque χCMR=∆L/2L il
fattore che descrive la capacità dell’apparato di rigettare forze comuni rispetto alle differenziali, abbiamo che la risposta dell’apparato a una forza comune è data da
(2) m F T x x x d CMR diff
χ
π
2 2 1 2 4 = − = ∆ 4. Il Segnale di Violazione 4. Il Segnale di Violazione 4. Il Segnale di Violazione 4. Il Segnale di ViolazioneGG è stato studiato per rilevare violazioni del principio di equivalenza avendo come sorgente del campo gravitazionale la terra. Similmente un modo di funzionamento di GGG in linea di principio potrebbe essere quello in cui la terra è la sorgente del segnale di violazione ripercorrendo il modello sperimentale del Barone von Eötvös. Se due corpi vengono, infatti, sospesi a filo a piombo in un laboratorio terrestre, la loro linea non indica il centro di massa della Terra, ma si dispone nella posizione di equilibrio lungo l’asse Nord-Sud in cui la forza centrifuga data dalla rotazione diurna della terra equilibra la gravità locale. Questo spostamento rispetto della perpendicolare rispetto al centro di massa della terra è il segno di un’accelerazione orizzontale lungo l’asse Nord-Sud che può essere la nostra sorgente per il Principio di Violazione. Infatti la posizione di equilibrio è data dall’interazione di una forza apparente centrifuga e una forza gravitazionale locale che la equilibra, se il principio di equivalenza fosse violato e la forza gravitazionale agisse in modo distinto sui due cilindri test l’intensità del segnale di violazione da rilevare sarebbe:
(1) aPE ηω⊕2R⊕cos(λL)sin(λL)
⊕
=
dove λL rappresenta la latitudine del laboratorio, R⊕ il raggio terrestre e
ω
⊕rappresenta la velocità anglare terrestre. Il valore massimo nell’intensità del segnale si raggiunge ad una latitudine di 45° dove il segnale di violazione raggiunge il valore di η1.7 10-2
m/sec2.
Un segnale di questa entità sarebbe perfetto come segnale sorgente terrestre, tuttavia la rotazione delle masse test rende impossibile l’utilizzo di tale segnale sorgente. Infatti un qualsiasi corpo sospeso a terra da un braccio l e dotato di momento angolare L è soggetto ad un effetto giroscopico dettato da
(2) l mg L L dt L d g − × Ω = × − × =
ω
⊕ (ω
⊕)dove il modulo Ωg=-mgl/L. Questo effetto di giroscopico è diretto esattamente
lungo la direzione del segnale di violazione, è molto più grande ed ha lo stesso periodo per cui non è rigettabile.
Viceversa l’apparecchiatura può essere usata a terra se si prende come sorgente del segnale di violazione il Sole. Prendere come segnale di violazione quello solare
Fourier. Quindi GGG può essere usato per verificare il principio di equivalenza nel campo gravitazionale solare e non in quello terrestre. L’intensità del segnale di violazione a terra dipende dalla posizione relativa del Sole rispetto al laboratorio ed è al massimo: (3) 2 0.6 10 2m/sec2 R GM aPE − Θ ⊕ Θ Θ ⋅ ⋅ = ≤
η
η
Con queste premesse GGG, al fine di verificare una fattibilità dell’ obiettivo di GG di raggiungere una precisione su η di 10-17, si pone l’obiettivo di verificare il
principio di equivalenza per un η di 10-13, un tale obiettivo richiede un sistema di
lettura capce di misurare uno spostamento di 10-13 m.
5. Il Sistema di Lettura Capacitivo 5. Il Sistema di Lettura Capacitivo 5. Il Sistema di Lettura Capacitivo 5. Il Sistema di Lettura Capacitivo
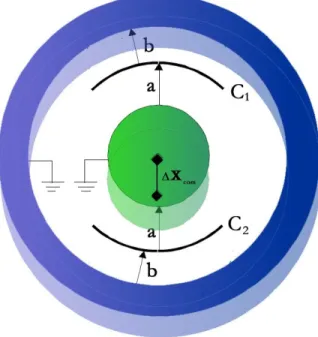
Per ottenere sistema di lettura con questa sensibilità è stato utilizzato un sistema di rilevazione basato sulla variazione di capacità. Fra le due masse test sono state inserite quattro piastre capacitive sospese al tubo di sospensione di modo che il sistema nel suo insieme possa essere interpretato come un ponte capacitivo dallo sbilanciamento del quale sia possibile dedurre lo spostamento comune e relativo fra le due masse test.
fig I.10: Il sistema di lettura capacitivo
Come risulta dalla figura (anche se per semplicità abbiamo riportato solo due piastre), alle piastre del condensatore viene applicato un segnale alternato Vin,
determinano la capcità dei condensatori e, dunque, un eventuale spostamento delle masse test provoca una variazione del segnale di uscita Vout che può essere
registrata.
Calcolando la capacità dei condensatori nell’approssimazione del condensatore piano (approssimazione accettabile considerando che la distanza è molto piccola rispetto alle dimensioni lineari delle piastre) troviamo che la capacità iniziale (supponendo le piastre perfettamente centrate) è data dalla formula:
(1) ab b a S b a S C C = + + = = 2 0 0 1 1 1 ε ε
Muovendosi le masse test fanno variare i parametri a e b, provocando così una variazione nella capacità dei condensatori. Prendiamo ad esempio uno spostamento comune delle due masse rappresentato come in figura.
fig I.11: spostamento comune delle due masse test
Le distanze relative (poniamo i pedici 1 e 2 in relazione alle distanze delle relative capacità) diventano (2) 1 2 2 1 1
,
,
∆
+
=
∆
−
=
∆
−
=
∆
+
=
com com com comx
b
b
x
a
a
x
b
b
x
a
a
(3) ∆ + + ∆ − = ∆ − + ∆ + = com com com com com com x b x a S C x b x a S C 1 1 1 1 0 2 0 1
ε
ε
Sottraendo abbiamo (considerando che a≅b>>∆xcom)
− + ∆ ≅ ∆ − − ∆ − ∆ = − 1 0 2 2 2 2 0 2 2 2 ) )( ( 2 1 1 2 b a b a b a x S x b x a x S C C com com com com com com
ε
ε
ovvero (4) − ∆ ≅ − ab b a x C C C com com com ) ( 2 0 1 2Ora invece analizziamo il comportamento del sistema difronte ad uno spostamento differenziale
fig I.12: spostamento differenziale delle due masse test Le distanze relative stavolta diventano
(5) ∆ + = ∆ + = ∆ − = ∆ − = diff diff diff diff x b b x a a x b b x a a 2 2 1 1 , ,
e le capacità si trasformano così in (6) ∆ + + ∆ + = ∆ − + ∆ − = diff diff diff diff diff diff x b x a S C x b x a S C 1 1 1 1 0 2 0 1
ε
ε
ottenendo così usando la stessa approssimazione precedente
+
∆
≅
∆
−
+
∆
−
∆
=
−
2 2 2 2 0 2 2 2 2 0 2 12
1
1
2
b
a
b
a
x
S
x
b
x
a
x
S
C
C
co com com diff diff diffε
ε
ovvero (7) + + ∆ ≅ − ) ( 2 2 2 0 2 1 b a ab b a x C C C diff diff diff Considerando che a b a ab b a 1 ) ( 2 2 ≅ + +abbiamo una formula semplificata per calcolare la variazione di capacità in funzione di uno spostamento generico ∆x. Abbiamo infatti che ∆xgen =∆xcom +∆xdiff per cui
(8) ∆ + ∆ − ≅ − diff com x a x a b a C C C 1 2 2 0 2 1
Il punto da notare in questa formula è che mentre la rilevazione dello spostamento differenziale in questa approssimazione non è influenzato dall’equidistanza delle due piastre, lo spostamento comune invece ha a numeratore un coefficiente di offset dovuto al posizionamento delle masse rispetto alle piastre che è (a-b). Uno spostamento dovuto ad una violazione del principio di equivalenza è uno spostamento differenziale che – dunque per essere rilevato – deve produrre un cambiamento nella capacità delle piastre maggiore del cambiamento prodotto dallo spostamento comune. Questo significa
(9) com xdiff a x a b a ∆ < ∆ − 1 2
(10) com diff x x a b a ∆ ∆ < −
Ovvero che il sistema di rilevazione in questione è molto più sensibile allo spostamento differenziale rispetto allo spostamento comune delle masse.
Per ottenere questa condizione è necessario che le masse sia centrate in modo da minimizzare il termine (a-b). Infatti la variazione di capacità dovuta allo spostamento comune dipende direttamente dalla differenza iniziale di distanza delle piastre dalle masse. In pratica, più le piastre sono centrate inizialmente, meno il sistema capacitivo è sensibile agli spostamenti comuni.
6. Controllo sui moti di whirl 6. Controllo sui moti di whirl 6. Controllo sui moti di whirl 6. Controllo sui moti di whirl
Come nel caso di GG, anche in GGG le masse sono poste in rotazione supercritica ottenendo così il duplice vantaggio di una modulazione discriminante del segnale di violazione con una riduzione del rumore elettrico e meccanico e di una riduzione della distanza relativa fra i centri di massa dovuta all’autocentratura che incorre nel rotore in regione supercritica. Questo è estremamente importante perchè realisticamente le due masse non possono essere centrate inizialmente se non con una precisione di 5-10 µm.
D’altra parte però la rotazione supercritica comporta una dissipazione energetica delle sospensioni meccaniche che produce un moto di whirl instabile la cui ampiezza cresce con il tempo in relazione all’inverso del quadrato del fattore qualità Q alla frequenza di spin. Le due masse sviluppano così un moto orbitale nel piano orizzontale del laboratorio attorno al loro punto di equilibro con la frequenza naturale delle oscillazioni differenziali.
Questi moti di whirl in GGG sono controllati attivamente da dei sensori/attenuatori capacitivi. Otto piastre capacitive simille alle piastre usate per la lettura del segnale, ma più piccole e meno sensibili, sono poste esternamente alla massa più esterna e fissate alla camera a vuoto. Quattro di queste capacità vengono utilizzate come sensori per rilevare spostamento e velocità del cilindro esterno e costruire così un comando di ammortizzazione elettrica. Le altre quattro capacità vengono utilizzate come attenuatori, ad esse infatti viene applicato un alto voltaggio (da 0 a 360 Volts) di modo da produrre una forza attiva che simuli un ammortizzatore non rotante.
Infine un ammortizzatore passivo e non rotante è posto sotto l’ultima sospensione laminare ed è utilizzato esclusivamente per passare la velocità critica del rotore.
Il funzionamento è semplice: un ago, la cui punta coincide, con il centro di massa del sistema è stato fissato sotto il cilindro interno e sotto di esso si trova il meccanismo di ammortizzazione costituito da un disco forato e da un piano. Con un impulso esterno alla camera a vuoto, il meccanismo si solleva e l’ago penetra nel foro centrale del disco metallico. In presenza di moti di whirl, l’ago trasporta il disco metallico sulla superficie del piano generando così le forze di attrito necessarie ad ammortizzare il sistema. Passata la velocità critica del rotore, un altro impulso fa sì che il
meccanismo si abbassi e sparisca l’ammortizzazione passiva.
7. Calibratura dell’accelerometro 7. Calibratura dell’accelerometro 7. Calibratura dell’accelerometro 7. Calibratura dell’accelerometro
Alcune operazioni di calibratura dell’accelerometro possono essere effettuate per ridurre alcuni errori sistematici dell’apparecchiatura. Un’inclinazione iniziale rispetto alla veritale delle braccia di accoppiamento può portare ad uno spostamento costante (nel riferimento rotante) fra le due masse. Per ridurre questo errore iniziale la posizione della sospensione superiore può essere aggiustata in modo da avere le tre sospensioni il più possibile in linea con la verticale. La calibrazione viene poi ulteriormente raffinata grazie all’uso di due piccole masse di 5 grammi ciascuna che possono essere spostate all’interno del braccio di accoppiamento per modificarne l’inclinazione. Per raffinare la calibratura ad un ordine superiore sono state disposte altre due masse del per di 0.5g ciascuna.
fig I.13: masse per la calibrazione dell’accelerometro
Un errore di inclinazione delle braccia della bilancia può essere simulato in modo identico da uno squilibrio elettrico fra le piastre capacitive. Pur essendo identici i due errori negli effetti prodotti, la sorgente di essi è radicalmente diversa e deve dunque essere discriminata. Il modo più semplice per operare tale discriminazione è quello di rilevare l’errore è quello di incrementare la velocità di rotazione del rotore fino a superare la frequenza naturale. Se l’errore di rilevazione è dettato dall’inclinazione le oscillazioni differenziali fra le due masse dovrebbero diminuire con il supermento della frequenza naturale, se ciò non avviene questo vuol dire che è necessario aggiustare le capacità variabili.
Un altra possibile sorgente di errore consiste nella non perfetta verticalità del tubo di sospensione, un’inclinazione in tale tubo di sospensione porta a rilevare un segnale differenziale costante fra le due masse che interferisce direttamente con il segnale di violazione. A prescindere da possibili errori nel montaggio del tubo di sospensione, questo effetto può rivelarsi molto insidioso quando è determinato dal rumore sismico.
8. Il Rumore Sismico 8. Il Rumore Sismico 8. Il Rumore Sismico 8. Il Rumore Sismico
Il rumore sismico è un rumore disturbante proveniente da perturbazioni sonore in senso lato che si trasmettono via terra. A parte disturbi sismici isolati, non periodici, di natura umana, i disturbi sismici più insidiosi sono quei disturbi di periodo giornaliero dettati dalla temperatura e dalla pressione durante il giorno. Nella categoria dei rumori sismici rientrano anche le accelerazioni orizzontali dell’apparecchio che (a causa del principio di equivalenza) non possono essere distinti dalle vere e proprie inclinazioni del piano orizzontale. Matematicamente parlando il rumore sismico può essere tradotto in un’inclinazione di un angolo α del piano orizzontale del laboratorio che si traduce in un angolo β del tubo di sospensione il quale
si trasforma in uno spostamento differenziale delle due masse test. Per stimare l’effetto in questione basta considerare che l’angolo β di equilibrio rispetto a quella che era la precedente verticale è dettato dalla condizione che la forza esercitata dalla sospensione k equilibri la variazione della componente orizzontale di g generata dalla rotazione del piano orizzontale.
La condizione di equilibrio per angoli sufficientemente
piccoli si traduce nella condizione: fig I.14: effetti dovuti al rumore sismico (1) mg kl kl + ≈
α
β
dove g è la gravità locale. Quando kl (come nel nostro caso) è molto minore di mg, abbiamo che (2) mg kl ≈
α
β
che –proprio per il motivo che kl è molto minore di mg- è molto minore di 1. Quindi già la scelta di sospensioni molto morbide e di masse molto pesanti offre una prima e naturale –anche se non sufficiente- attenuazione dell’inclinazione dell’orizzontale dovuta al rumore sismico.
(3) − ≈ mg kl g a 1
α
γ
A causa di questa accelerazione la verticale del laboratorio cambia di un angolo α dato dalla somma vettoriale di g e di a. In effetti questo è vero solo se si assume valido il Principio di Equivalenza, ma a questi livelli di approssimazione tale principio può essere certamente preso come valido. Per cui lo spostamento β della sospensione dalla nuova verticale del laboratorio è di
(4) mg kl mg kl g a
α
γ
α
β
= − ≈ =Ovvero simile allo spostamento nel caso di inclinazione del piano orizzontale. Per ottenere una stima quantitativa del fenomeno, l’apparato è stato monitorato con l’accelerometro ISA (Italian Space Accelerometer) che ha decretato un’ampiezza giornaliera del fenomeno di circa 10-6 radianti, i quali producevano uno spostamento relativo fra le due masse test dell’ordine di 10-7 metri. La
precisione che si vuole raggiungere con l’esperimento GGG ha dunque richiesto la rilevazione e l’attenuazione di questo rumore sismico. Per fare questo è stato installato un tiltmetro sulla camera a vuoto capace di rilevalere oscillazioni rispetto alla verticale dell’ordine di 10-10 rad che corrispondono a spostamenti relativi dell’ordine di 10-11 metri e che vengono attenuati attivamente con delle piezoceramiche applicando loro un voltaggio di 0.1 mV. Altri tre o quattro ordini di grandezza possono essere guadagnati sospendendo la camera a vuoto con un giunto cardanico che funge da attenuatore passivo.
II. Elementi Dinamica dei Rotori II. Elementi Dinamica dei Rotori II. Elementi Dinamica dei Rotori
II. Elementi Dinamica dei Rotori Supercritici Supercritici Supercritici Supercritici
In questo capitolo verranno presentati la nomenclatura e gli elementi basilari di Dinamica dei Rotori che verranno poi utilizzati nella seconda e nella terza parte della Tesi.L’obiettivo di questo capitolo è quello di fornire il minimum teorico e pratico necessario al fine di poter approcciare i capitoli successivi.
Gli esempi presentati saranno quindi i più semplici possibile al fine di introdurre esclusivamente i concetti chiave che serviranno a comprendere qualitativamente il comportamento dei rotori in generale e che verranno poi utilizzati nella loro reale applicazione specifica nei capitoli successivi. Per una trattazione esaustiva sull’argomento, quindi, rimandiamo ai [12]-[13] della bibliografia.
1. Concetti Base 1. Concetti Base 1. Concetti Base 1. Concetti Base
La definizione di rotore è quella di un corpo sospeso tramite un insieme di supporti cilindrici ruotante attorno ad un asse la cui direzione è fissa nello spazio inerziale. Un semplice modello di rotore è quello
rappresentato in figura.
Il rotore in questione è qui rappresentato nella sua configurazione non deformata. Il rotore propriamente detto è il corpo centrale della figura con centro di massa G e punto di sospensione C attraverso il quale passa l’albero che rappresenta l’asse di rotazione. I due supporti che reggono l’albero nella sua rotazione vengono comunemente chiamati statori e sono supposti fissi.
Il rotore invece ruota attorno all’asse, indicata dalla direzione dell’albero nella configurazione priva di deformazioni, con una velocità angolare ωs . La distanza
fra CG viene chiamata eccentricità e verrà indicata con il vettore
ε
. E’ importante notare che in generale, nel mondo fisico reale, l’eccentricità è sempre presente, cioè nella pratica non è possibile farcoincidere perfettamente il centro di massa con il punto di sospensione, per cui realisticamente l’albero non rappresenta l’asse principale di inerzia del corpo. Dato un sistema del genere, le soluzioni dell’equazione caratteristica associate all’equazioni del moto del sistema sono chiamate frequenze naturali del sistema. Le velocità per le quali una delle forze agenti sul rotore ha una frequenza pari ad una delle frequenze naturali del rotore, vengono chiamate velocità critiche.
A queste velocità critiche incorrono fenomeni di risonanza per cui si assiste ad un crescere lineare nel tempo delle vibrazioni che possono portare eventualmente alla distruzione stessa del rotore. In particolare una velocità critica è quella in cui la velocità di rotazione ha una frequenza pari alla frequenza naturale. La prima velocità critica del sistema discrimina il range di velocità chiamato subcritico dal range di velocità chiamato supercritico. Come abbiamo visto nel capitolo precedente, sia GG che GGG sono stati ideati e sono pienamente operativi in un regime supercritico. Questa scelta di lavoro comporta molti vantaggi (alcuni dei quali sono già stati accennati), ma comporta anche il necessario superamento di una velocità critica. Il modo migliore per comprendere il fenomeno è l’esempio quotidiano di una lavatrice in fase di centrifuga. Man mano che il cestello della lavatrice aumenta la propria velocità angolare avvicinandosi alla velocità critica, le vibrazioni meccaniche aumentano sempre di più, finchè –una volta superata tale velocità- esso non entra in un regime supercritico, si autocentra e le vibrazioni
guadagno di circa tre ordini di grandezza nell’errore iniziale di dislocazione, ma il poter lavorare in questo ambiente implica il superare almeno una velocità critica e quindi essere pronto a poter sopportare un’incremento delle vibrazioni meccaniche.
Oltre alla velocità critica dettata dalla frequenza naturale del sistema, nel caso di rotori puri, privi di un sistema di ammortizzazione non rotante, vi sono anche delle precise regioni di instabilità in cui le vibrazioni meccaniche non vengono disperse dal sistema di ammortizzazione, ma anzi vengono aumentate da esso. Nel caso di un rotore con un ammortizzatore non rotante (cioè facente parte dello statore) l’ampiezza delle oscillazioni libere decade perchè l’energia cinetica di tali vibrazioni viene dissipata dall’ammortizzatore. Nel caso invece di un’ammortizzazione rotante, le oscillazioni libere a certe frequenze possono essere autoeccitate dal sistema di ammortizzazione e compromettere seriamente il corretto funzionamento del rotore.
Queste regioni di instabilità sono tutte situate in regime supercritico e mentre è possibile passare la velocità critica ed entrare in regime supercritico, è necessario stare attenti a non entrare nelle regioni di instabilità nelle quali è impossibile lavorare correttamente.
2. Rotazione supercritica ed 2. Rotazione supercritica ed 2. Rotazione supercritica ed
2. Rotazione supercritica ed autocentratura del rotoreautocentratura del rotoreautocentratura del rotoreautocentratura del rotore
Con l’entrata del rotore nel regime supercritico abbiamo un fenomeno comunemente chiamato autocentratura del rotore. A queste
velocità il rotore comincia a ruotare attorno al proprio centro di massa invece che al proprio centro di sospensione eliminando virtualmente l’eccentricità incorsa nella composizione del rotore. Il modo più semplice per illustrare questo fenomeno è quello di prendere in considerazione un rotore formato da un corpo puntiforme G sospeso nel punto C ad un albero privo di massa e di costante elastica k. Definiamo ) , (x y OC r= = )) sin( ), cos( (x t y t OG rG= = +
ε
ω
s +ε
ω
s )) cos( ), sin( (x t y tr&G= &−
ω
sε
ω
s &+ω
sε
ω
sChiamiamo T l’energia cinetica e U l’energia potenziale e abbiamo (1) L=T −U (2) ( ) 2 1 2 2 y x k U = + (3)
[
2 ( cos( ) sin( ))]
2 1 2 2 2 2 t x t y y x mT = & + & +ε ωs + εωs & ωs − & ωs
Da cui, secondo il formalismo Lagrangiano, nelle coordinate x e y e considerando la velocità angolare costante, otteniamo le due equazioni del moto:
(4)
[
]
[
]
= + − = + − 0 ) sin( 0 ) cos( 2 2 ky t y m kx t x m s s s sω
εω
ω
εω
& & & &mettendo il sistema in forma complessa con z=x+iy otteniamo l’equazione differenziale (5) s i t s e m kz z m
εω
2 ω = + & &La soluzione generale dell’omogenea associata è
(6) mt k i t m k i om t ze z e z − + = 1 2 ) (
La quale ci indica la velocità critica del sistema (chiamata anche velocità di whirl) che è
m k
cr =
ω
e descrive l’equazione di quelle oscillazioni libere che saranno i moti di whirl del sistema in regime supercritico e che avvengono con frequenza relativa alla velocità critica del sistema. In particolare poichè i segni delle velocità angolari sono opposti, questi moti saranno la composizione di due moti circolari distinti uno diretto (concorde con la velocità angolare del rotore) e uno inverso (opposto ad essa). Il moto risultante dalla combinazione lineare di questi due moti circolari potrà risultare essere circolare, ellittico o lineare a seconda dei coefficienti.Una soluzione particolare del sistema invece è
(7) i t s cr s t i p s s e e z t z ω ω
ω
ω
ω
ε
2 2 2 0 ) ( − = =(8) 2 2 (cos( ),sin( )) 2 t t r s s s cr cr G
ω
ω
ω
ω
ω
ε
− =Questo è quello che ci serve per comprendere l’effetto di una rotazione supercritica. Studiamo infatti il termine
(9) 2 2 2 2 2 2 1 1 cr s cr s cr cr
ω
ω
ω
ω
ω
ω
− = −dal quale è direttamente proporzionale il modulo rG , se
2 2
cr
s
ω
ω
<< siamo in regime subcritico ed il coefficiente si riduce ad una costanteω
cr2 , se la velocità angolare èparagonabile alla velocità critica, il denominatore cresce indiscriminatamente, se, invece
ω
s2 >>ω
cr2 ecco che il vettore indicante il centro di massa può essere scrittonella sua forma approssimata
(10) 2 0 2 ≅ ≅
ε
ω
ω
s cr G rQuindi la distanza fra l’asse di rotazione e il centro di massa tende a sparire e il rotore comincia a ruotare attorno al proprio centro di massa invece che al proprio punto di sospensione. Questo fenomeno è chiamato autocentratura del rotore in regione supercritica. In effetti riportiamo in figura i valori per il modulo del vettore rG in
relazione alle velocità di spin.
fig I.16: distanza del c.m. del rotore elementare dall’asse di rotazione in funzione della frequenza di spin
3. L’attrito viscoso e i moti di whirl 3. L’attrito viscoso e i moti di whirl 3. L’attrito viscoso e i moti di whirl 3. L’attrito viscoso e i moti di whirl
I moti di whirl sono i moti liberi che incorrono in un sistema rotante in regime supercritico dovuti alla dissipazione di energia. La dissipazione di energia in un sistema rotante può risolversi ambivalentemente in un’incremento dei moti liberi del sistema, come in una loro attenuazione. In generale dunque la dissipazione di energia può avere un effetto stabilizzante del sistema oppure destabilizzante dando luogo a dei moti di whirl. Per l’analisi dei nostri moti di whirl considereremo una dissipazione di energia dovuta all’attrito viscoso (cioè dipendente linearmente dalla velocità lineare del sistema).
In primo luogo, per una corretta analisi del fenomeno, è necessario distinguere due forme di attrito viscoso, la prima relativa all’interazione fra rotore e statore, dunque una forma di attrito non rotante e la cui dispersione di energia è proporzionale alla velocità relativa tra riferimento del laboratorio e riferimento solidale con il rotore; la seconda invece è una forma di attrito rotante, relativa all’energia dissipata dal rotore stesso e proporzionale alla velocità relativa nel riferimento solidale con il rotore. Per essere più chiari, una forza di attrito viscoso agente sul sistema può essere decomposta in due componenti:
(1) Fatt =Frot +Fnrot
Introducendo come in precedenza una coordinata complessa z che rappresenti il piano xy ortogonale all’asse di rotazione nel riferimento non rotante del laboratorio, e chiamando invece ζ la coordinata complessa che individui lo stesso piano ma nel riferimento solidale con il rotore, avremo che
(2) Fnrot =−cnrotz& e
ς
&rot rot
c F =−
Dove ciascuna forza è considerata nel proprio riferimento. Poichè la coordinata ζ può essere scritta in funzione di z come (3)
ς
= ze−iωst e s i t s e z i zω
ως
− − = ( & ) &abbiamo che, sempre nel riferimento rotante, ma scritta in funzione di z
(4) rot s i t rot c z i z e s F
ω
−ω − − = ( & )ovvero leggendo questa equazione nel riferimento del laboratorio e sommandola all’equazione relativa all’attrito non rotante, otteniamo: (5) Fatt =−crot(z&−i
ω
sz)−cnrotz& =−(cnrot +crot)z&+icrotω
sz(6) rot nrot s rot s i t s e m z c i k z c c z
m&&+( + )&+( −
ω
) =εω
2 ωLa soluzione particolare del nuovo sistema cambia quantitativamente ma non qualitativamente assicurando così che il fenomeno di autocentratura per velocità supercritiche, rimane essenzialmente immutato. Infatti
(7) i t nrot s s cr s t i p s s e m c i e z t z ω ω
ω
ω
ω
ω
ε
+ − = = 2 2 2 0 ) (e non cambia l’andamento qualitativo del centro di massa per velocità angolari molto superiori alla velocità critica.
Quella che invece cambia radicalmente è la soluzione omogenea, le due soluzioni dell’equazione caratteristica diventano infatti
(8) 2 2 2 , 1 4 ) ( ) ( 4 2 m c c c i k m m c c
i rot + nrot ± − s rot − rot + nrot
=
ω
λ
e la soluzione omogenea diventa
(9)
z
omt
z
e
te
i tz
e
te
i t ) Re( ) Im( 2 ) Re( ) Im( 1 2 2 1 1)
(
=
− λ λ+
− λ λOvvero la combinazione lineare di due moti circolari come nel caso precedente, ma stavolta con ampiezze dipendenti dal tempo. Per quanto riguarda la direzione di questi due moti, è facile trovare che supponeno una velocità di rotazione molto maggiore della velocità critica, allora Re(
λ
1)≅−ω
cr e Re(λ
2)≅ω
crper cui i duemoti sono rispettivamente inverso e diretto rispetto alla rotazione del rotore. Per quanto riguarda, invece, l’ampiezza di questi moti abbiamo che i coefficienti z1 e z2
sono moltiplicati per dei termini che sono funzione esponenziale del tempo e che possono crescere o diminuire in relazione del fatto che la parte immaginaria della soluzione sia negativa o positiva. Per quanto riguarda λ1, con un po’ di manipolazioni
algebriche ordinarie è facile vedere che la parte immaginaria è positiva per ogni frequenza di spin per cui il moto di whirl contrario alla direzione di rotazione è in realtà ammortizzato dall’attrito viscoso per ogni frequenza di rotazione. Viceversa si dimostra facilmente che la parte immaginaria di λ2 è positiva (e dunque il moto di
whirl è attenuato) solo nel caso
(10) (1 ) rot nrot cr s c c + <
ω
ω
Questa condizione permette di illustrare un fenomeno di carattere molto più generale del rotore preso in considerazione.
In generale l’attrito non rotante ha un effetto stabilizzante sui moti di whirl. Più esso è grande più la regione di instabilità si allontana dalla velocità critica, permettendo così di lavorare in una regione supercritica ma non instabile. Viceversa se esso è zero, oppure molto inferiore all’attrito rotante, abbiamo che per ogni velocità maggiore della velocità critica i moti di whirl sono instabili e crescono in ampiezza secondo una legge dipendente esponenzialmente dal tempo. Riassumendo l’analisi fatta sul nostro rotore esemplare, i concetti che possono essere generalizzati sono i seguenti:
1. I moti di whirl inversi sono sempre stabili
2. L’attrito viscoso non rotante ha un effetto stabilizzante sui moti di whirl diretti
3. In caso di assenza o insufficienza di attrito viscoso, i moti di whirl diretti crescono in ampiezza secondo una legge che dipende esponenzialmente dal tempo
4. Nel caso di velocità di rotazione molto maggiore della velocità critica, i moti di whirl hanno frequenza pari alla frequenza naturale del sistema.
4 44
4. L’ anisotropia n. L’ anisotropia n. L’ anisotropia n. L’ anisotropia nella costante elastica ella costante elastica ella costante elastica ella costante elastica
Un ultimo argomento che risulterà utile in seguito è quello di studiare il comportamento di un rotore supercritico in presenza di anisotropia della costante elastica. In presenza di anisotropia della costante elastica le frequenze naturali si raddoppiano e quella che, nel caso ideale era un’unica frequenza naturale, si scinde in due frequenze naturali separate l’una dall’altra da un fattore dipendente dall’anisotropia della costante. Questo fenomeno è abbastanza comprensibile se si considera che un modello matematico per tale sistema fisico può essere rappresentato non più da un’unica molla con simmetria radiale, bensì da due molle ortogonalmente disposte sul piano con due costanti elastiche diverse e dunque con due frequenze naturali distinte legate dal fattore di anisotropia. Ciò che è meno intuitivo e per cui è utile svolgere compiutamente l’esempio è che una di queste frequenze naturali risulta essere dipendente dalla velocità di rotazione del sistema e questa dipendenza darà origine alla comparsa di intere regioni di instabilità che avranno estensione non nulla.
Il modello più semplice per studiare in modo esemplificativo il fenomeno in questione è quello di prendere in considerazione il rotore che abbiamo considerato nel paragrafo II.1 in cui l’albero del rotore presenta delle caratteristiche di anisotropia elastica. Supponendo di spostarci nel sistema di riferimento rotante ( O, ξ, η, z), l’anisotropia elastica dell’albero si traduce nel richiedere che la costante elastica kξ sia
definiamo α come l’angolo fra il vettore CG e l’asse delle ξ di modo che ) 0 ), sin( ), (cos(α α ε
ε = sia l’eccentricità, a questo punto abbiamo che ) 0 , , (
ξ
η
ε
+ = = OGrG e & =(
ξ
&,η
&,0)G
r
A questo punto, chiamando ωs =ωs(0,0,1), scriviamo la Lagrangiana del sistema
(1) = mvin−U = m
(
rG+ s×rG)
−U 2 2 ) ( 2 1 2 1ω
& r LEssa può essere suddivisa in quattro termini fondamentali, se chiamiamo termini di energia cinetica i termini dipendenti solo dalle derivate temporali delle coordinate e termini di energia potenziale quelli che sono semplicemente funzioni delle coordinate, abbiamo un termine di energia cinetica e tre termini potenziali cioè:
(2) ( ) 2 1 2 1 2 2 2
η
ξ
& & & = + = mr m Tcin G (3) ( 2 cos( ) 2 sin( ) ) 2 1 ) ( 2 1 2 2 2 2 2ε
α
εη
α
εξ
η
ξ
ω
ω
× = + + + + = s G s centr m r m U(4) = & ⋅(
ω
× )=−ω
(ξ
&η
−η
&ξ
)s G s G cor mr r m U (5) ( ) 2 1 2 2
η
ξ
η ξ k k U = +Questa nomenclatura è un po’ artificiosa, ma comoda in quanto permette di discriminare rapidamente le componenti che dipendono solo dalle velocità rispetto a quelle che dipendono anche dalle coordinate. Componendo i termini abbiamo che (6) L=Tcin +Ucentr +Ucor −U
Non essendo in presenza di attrito o forze non derivabili da potenziali, abbiamo che le equazioni del moto possono essere scritte con la solita formula:
(7) = ∀ ∈
{
ξ
,η
}
∂ ∂ ∂ ∂ i i i q q q dt d 0 L -L &Da queste equazioni si deriva il sistema:
(8)
(
)
(
)
= − + + − = − + + − − 0 ) sin( 0 ) cos( 2 2 2 2η
ξ
ω
α
ε
ω
η
ω
ξ
ω
η
ξ
η
ω
α
ε
ω
ξ
ω
η
ω
ξ
η ξ k m m m m m k m m m m m s s s s s s s s & & & & & & & &Ovvero in forma matriciale (9) Mq&&+Bq&+Aq=
ε
' dove abbiamo definito =
η
ξ
q , = m m M 0 0 , − = 0 2 2 0 s s m m Bω
ω
− − = 2 2 0 0 s s m k m k Aω
ω
η ξ e = ) sin( ) cos( ' 2α
α
ε
ω
ε
m sPer trovare le posizioni di equilibrio basta imporre q&&= q& =0e troviamo
(10) − − = = − 2 2 2 2 1 ) sin( ) cos( ' s s s s eq m k m m k m A q
ω
α
ε
ω
ω
α
ε
ω
ε
η ξLe due velocità critiche sono dove si annulla il denominatore, per semplicità chiamiamole m kξ ξ
ω
2 = e 2 ξ2 η ηω
ω
= =Λ m kA questo punto per vedere i moti di whirl possibili cerchiamo le soluzioni dell’omogenea.
Per rendere il sistema del primo ordine definiamo il vettore u=(q,q&)te scriviamo dunque l’equazione omogenea come
(11) u u B M A M Id u =Ω − − = 0−1 −1 &
L’equazione caratteristica associata al sistema è
(12) det(Ω−
λ
Id)=λ
4 −λ
2(2ω
s2 +ω
η2 +ω
ξ2)+(ω
ξ2 −ω
s2)(ω
η2−ω
s2)=0 ovvero(13) 2 ) )( ( 4 ) 2 ( ) 2 ( 2 2 2 2 2 2 2 2 2 2 2 2 , 1 2
ω
sω
ω
ω
sω
ω
ω
ω
sω
ω
sλ
= + η + ξ ± + η + ξ − ξ − η −Considerando che
ω
η2 =Λω
ξ2 , con qualche manipolazione algebrica ordinariaabbiamo che (14)
(
)
2 ) 1 ( 8 ) 1 ( ) ) 1 ( 2 ( 2 2 2 2 2 2 2 , 1 2ω
sω
ω
ω
ω
sλ
= + Λ+ ξ ± ξ Λ− ξ + Λ+Per il momento siamo interessati a studiare la stabilità del sistema in questione, quindi a capire se gli autovalori della matrice sono reali o immaginari, in questo senso, come prima cosa, notiamo che ∆=
ω
ξ2(
(Λ−1)2ω
ξ2 +8(Λ+1)ω
s2)
≥0sempre, quindi i λ2 sono sempre reali. Viceversa se introduciamo il parametro adimensionaleξ
ω
ω
ω
s=
' abbiamo che la condizione sugli autovalori affinchè essi siano reali si può semplicemente tradurre nella condizione
(15) (
ω
'2−1)(ω
'2−Λ)≥0Tale condizione è realizzata ovunque meno che nella regione 1<
ω
' < Λ ovvero Considerando le frequenze positive il sistema è instabile nella regioneη
ξ
ω
ω
ω
< '<Un altro fatto importante da notare è la dipendenza degli autovalori dalla frequenza di rotazione: a differenza dei casi precedenti, stavolta la frequenza dei moti di whirl dipende direttamente dalla frequenza di rotazione. Cerchiamo di studiare qualitativamente il comportamento di questi moti. Fino ad adesso abbiamo sviluppato la nostra teoria nel riferimento rotante, adesso e meglio riportarci al riferimento non rotante perchè sarà principalmente in quel riferimento che illustreremo i risultati relativi a GGG.
Chiamiamo ξ
ω
ω
λ
nrnr = , le frequenze di whirl nel riferimento non rotante saranno
allora date da (16)
(
)
2 ' ) 1 ( 8 ) 1 ( )) 1 ( ' 2 ( ' 2 2 2 4 , 3 , 2 , 1ω
ω
ω
λ
nr = ± + Λ+ ± Λ− + Λ+per studiare il comportamento di tali soluzioni in regime supercritico cioè con ∞
→ '
(17) − Λ + + Λ ± + Λ + ± = 4 2 2 2 4 , 3 , 2 , 1 ' 4 ) 1 ( ' ) 1 ( 2 ' 2 ) 1 ( 1 1 '
ω
ω
ω
ω
λ
nrper ottenere che ' 2 3 , 1
ω
λ
ω → →∞ nrDove abbiamo considerato che le soluzioni 1, 3 fossero quelle con radicale esterno positivo. Per quelle, invece, con radicale negativo, il termine dominante è un’altro:
(18) ξ ξ η ω
ω
ω
λ
k k k nr 2 2 ) 1 ( ' ) 1 ( 2 1 1 ' 4 , 2 + ± = Λ + ± ≈ Λ+ ± − → →∞ovvero, in regime supercritico queste soluzioni sono costanti (almeno al primo ordine di approssimazione) cioè indipendenti dalla frequenza di rotazione e chiamando (19) m k k k k k k m m m ⇒ =± =± + = ξ ξ ξ η
ω
ω
4 , 2 2Cioè, viste dal riferimento non rotante, con limite della rotazione supercritica le due soluzioni tendono ad essere indipendenti dalla velocità di rotazione e a comportarsi come soluzioni di un rotore con costante elastica isotropa pari alla media delle due costanti elastiche.
Dunque rissumendo i risultati importanti di questo paragrafo abbiamo che in presenza di anisotropia della costante elastica abbiamo che
1. Le frequenze dei moti di whirl si raddoppiano dividendosi per una quantità dipendente dall’anisotropia della costante
2. Per ωξ<ωs<ωη compaiono delle regioni in cui il sistema è
instabile
3. In generale le frequenze dei moti di whirl dipendono dalla velocità della rotazione del rotore
4. Due di queste frequenze nel limite supercritico tendono a crescere linearmente (con un fattore 2) rispetto alla frequenza di rotazione
isotropa pari alla media delle due costanti elastiche e quindi a rimanere costanti.