1
Indice
Introduzione
I I modelli
1. Stati eccitati in soluzione
1.1 Il modello di solvatazione PCM
1.1.1 Formulazione standard per gli stati d’equilibrio 1.1.2 Estensione agli stati di non –equilibrio
1.2 Metodi Linear Response 1.2.1 TDDFT
1.2.2 Uso dell’IEFPCM nel metodo TDDFT 2. Il modello per il metallo
2.1 Proprietà plasmoniche
2.1.1 Effetto delle nanoparticelle metalliche sui processi fotofisici 2.2 Il modello IEFPCM per il metallo
2.2.1 Estensione del modello alla trattazione degli stati eccitati 3. Energy Transfer in ambienti complessi
3.1 Il modello di Förster
3.2 Il modello di tipo IEFPCM-TDDFT
3.2.1 Estensione del modello: approccio QM/MMPol/PCM polarizzabile 3.3 Effetti del solvente
3.4 Effetti di un ambiente complesso
II Applicazioni
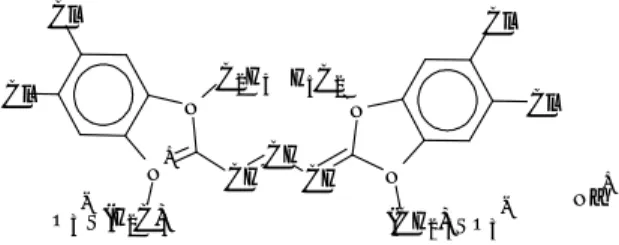
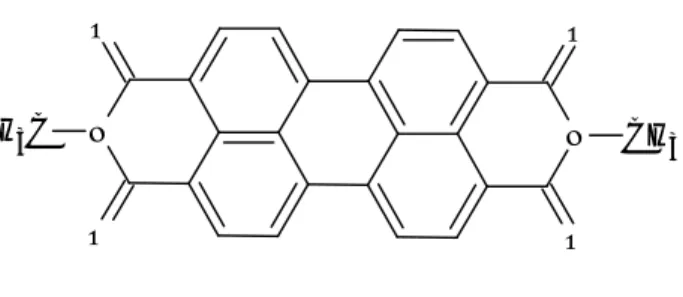
4. Studio del sistema modello PDI
4.1 Descrizione del sistema e dei processi fisici attivi 4.2 Risultati dei calcoli e discussione
4.2.1 Studio sistematico dell’entità relativa dei processi attivi nel sistema 4.2.2 Studio delle condizioni di amplificazione dell’intensità luminosa emessa 4.3 Conclusioni
5. Studio di sistemi fotosintetici 5.1 Peridinin-Chlorophyll-Protein 5.1.1 Presentazione del sistema
5.1.2 Descrizione delle proprietà spettroscopiche dei pigmenti 5.1.2.1 Peridinina
5.1.2.2 Clorofilla a
2
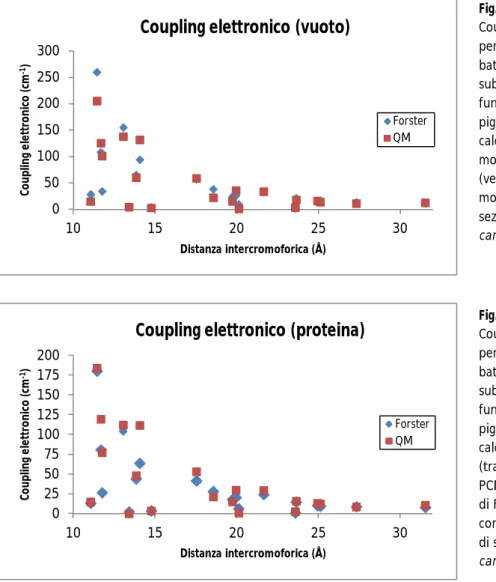
5.1.3 Determinazione dei coupling elettronici in vuoto e nella proteina
5.1.3.1 Confronto con i coupling elettronici calcolati in ambiente PCM/MMPol 5.1.3.2 Confronto con i coupling elettronici calcolati con la teoria di Förster 5.1.4 Effetto di nanoparticelle metalliche sull’Energy Transfer nella PCP
5.2 Fenna-Matthews-Olson protein 5.2.1 Presentazione del sistema
5.2.2 Determinazione dei coupling elettronici in vuoto e nella proteina
5.2.3 Effetto di nanoparticelle metalliche sull’Energy Transfer nella proteina FMO Conclusioni
Ringraziamenti
3
Introduzione
Negli ultimi decenni si è assistito al rapido sviluppo della branca della chimica teorica che va sotto il nome di chimica computazionale. Essa si occupa dello sviluppo e dell’implementazione di modelli matematici in grado di simulare sistemi chimici, con lo scopo di calcolarne le grandezze fisiche caratteristiche e di prevederne le proprietà chimiche. I notevoli sforzi profusi nella formulazione di metodi sempre più accurati, uniti alla disponibilità di risorse di calcolo crescenti, hanno reso possibile lo studio di sistemi di complessità via via più elevata. In questo consolidato quadro si inserisce il presente lavoro di tesi, il cui oggetto è un’indagine, condotta con mezzi computazionali, dei meccanismi microscopici alla base dei fenomeni di Electronic Energy Transfer in ambiente complesso.
Il processo fotofisico noto come Electronic Energy Transfer (EET) o, alternativamente, Resonance Energy Transfer (RET), è ubiquitario in natura. Esso consiste nel trasferimento di energia di eccitazione da una molecola “donatore” (D) inizialmente eccitata a una molecola “accettore” (A) [1]. Il donatore tipicamente emette in un range di lunghezze d’onda che si sovrappone con lo spettro di assorbimento dell’accettore, tuttavia è bene precisare sin da subito che l’energia di eccitazione non si trasmette attraverso eventi non correlati di emissione del donatore ed assorbimento dell’accettore, ovvero non si registra la comparsa di alcun fotone. E’ piuttosto l’interazione, di natura prevalentemente coulombiana, tra tali molecole a determinare una reazione in cui la molecola di donatore è diseccitata e l’energia elettrostatica è trasferita alla molecola di accettore che viene così eccitata [2]:
∗
+
⟶
+
∗Il processo può avvenire anche se entrambe le molecole sono spazialmente separate e, assumendo per semplicità che esse siano descrivibili in termini di due soli orbitali, HOMO e LUMO, può essere così schematizzato:
J J
Lo studio sia teorico che sperimentale dei fenomeni di Electronic Energy Transfer vanta una lunga e consolidata tradizione. Tali fenomeni sono stati dapprima osservati in soluzioni di coloranti (per esempio, isocianine e pseudo-isocianine, Fig. II) e poi evidenziati in diversi sistemi biologici. In particolare, essi rivestono un ruolo chiave nei processi fotosintetici (light harvesting) attivi in piante, alghe e batteri: in tali organismi l’energia solare assorbita è infatti convogliata ai centri di reazione in modo direzionato grazie a una sequenza di trasferimenti energetici [3]. Questi ultimi si realizzano per mezzo di complessi proteici detti antennae, i quali contengono generalmente due tipi di pigmenti: (batterio)clorofille e carotenoidi (Fig. III).
∗ ∗
Fig. I
L’interazione prevalentemente coulombiana J promuove lo scambio di energia di eccitazione tra donatore (D) ed accettore (A).
4 N N CH CH CH N N+ Cl Cl H5C2 (CH2)4SO3 -C2H5 O3-S(H2C)4 Cl Cl Na+
Il vasto interesse suscitato dai fenomeni di Electronic Energy Transfer si giustifica alla luce delle molteplici applicazioni di questi ultimi. L’applicazione più comune è la misura delle distanze tra due siti in una macromolecola; tipicamente essa è realizzata legando covalentemente a una proteina un donatore e un accettore e valutando l’efficienza dell’EET tramite misure allo stato stazionario dell’entità del quenching del donatore da parte dell’accettore [4]. Uno sforzo considerevole è stato inoltre profuso nello sviluppo di celle solari efficienti basate sul fenomeno dell’EET osservato nei sistemi fotosintetici naturali; nondimeno, la comprensione dei meccanismi alla base dell’EET è determinante ai fini dell’ottimizzazione di sensori con funzionamento basato sulla fluorescenza e di LED (Light Emitting Diodes) organici e polimerici.
Esistono poi diversi studi teorici e sperimentali sull’Energy Transfer da molecole organiche a superfici metalliche planari o sferiche [5], nonché sull’Energy Transfer tra nanoparticelle metalliche o tra nanoparticelle di semiconduttore in presenza di nanocristalli metallici [6]. Sebbene nel caso delle nanoparticelle metalliche il meccanismo fisico sotteso all’Energy Transfer sia lo stesso che nel caso di cromofori organici, è importante notare che qui l’energia è trasferita ai modi plasmonici confinati alla superficie del metallo. L’impiego di nanoparticelle e film metallici negli esperimenti di Energy Transfer presenta diversi vantaggi, per esempio può permettere il trasporto direzionato di energia di eccitazione da molecole di donatore a molecole di accettore situate agli estremi opposti di un film metallico [7], oppure determinare un incremento dell’assorbimento di luce negli apparati fotosintetici [8] con eventuale conseguente enhancement dell’intensità di luce emessa dalle molecole di accettore [9, 10].
Uno tra i fini ultimi del dettagliato studio dei fenomeni di Energy Transfer può essere individuato nell’acquisizione delle conoscenze necessarie per la realizzazione di apparati fotosintetici artificiali ad efficienza ottimizzata. A questo scopo è di fondamentale importanza la comprensione, a livello molecolare, di tali fenomeni e delle modalità secondo cui essi sono influenzati dall’ambiente. E’ proprio in quest’ottica che i moderni mezzi teorico-computazionali rivelano tutta la loro utilità e si configurano come un imprescindibile supporto all’indagine sperimentale dei processi di EET. Nel filone di ricerca fin qui delineato si inserisce il presente lavoro di tesi, in cui particolare attenzione è stata rivolta agli effetti dell’ambiente sui fenomeni di Energy Transfer tra molecole organiche. Per ambiente si intende qui un intorno complesso, costituito da diverse componenti: mezzo solvente, matrice proteica, nanoparticelle metalliche, etc. La varietà e complessità delle interazioni che accoppiano le diverse porzioni del sistema totale, nonché le differenti scale temporali e dimensionali coinvolte nei processi in gioco, rendono l’obiettivo di una descrizione molecolare dei fenomeni trattati estremamente ambizioso. La strategia qui adottata per far fronte all’oggettiva complessità del problema è consistita nell’accoppiamento di metodi quanto-
Fig. II
Esempio di colorante: TDBC (5,5’,6,6’-tetrachloro-1,1’-diethyl-3,3’-di(4-sulfobutyl)-benzimidazolcarbocyanine).
Fig. III
I pigmenti attivi nel Light Harvesting Complex II (LHC II) del batterio Rps. Acidiphila: batterioclorofille (rosso e verde) e carotenoidi (giallo).
5
meccanici con approcci classici: i primi sono stati impiegati per descrivere accuratamente le porzioni di sistema direttamente coinvolte nei processi di EET, i secondi per introdurre, secondo vari gradi di approssimazione, l’effetto dell’ambiente su tali processi.
Il presente elaborato di tesi è suddiviso in due sezioni principali: la prima è dedicata alla presentazione dei fenomeni fisici trattati e della loro modellizzazione, la seconda all’esposizione di alcune applicazioni e dei relativi risultati.
Più nel dettaglio, nella prima sezione saranno descritti i metodi di tipo Linear Response per stati eccitati in vuoto e la loro estensione al caso in solvente (trattato, quest’ultimo, secondo il Polarizable Continuum Model). La presentazione di questi metodi si rende necessaria in quanto essi vengono impiegati per il calcolo delle proprietà di transizione elettronica dei cromofori, a partire dalle quali è possibile calcolare le quantità caratteristiche dei processi di Energy Transfer senza dover ricorrere alle approssimazioni di tipo dipolare comunemente impiegate (modello di Förster [11]). Sarà quindi presentata la teoria delle proprietà plasmoniche dei metalli e del loro effetto sui processi di decadimento di molecole eccitate, nonché la relativa modellizzazione. Seguirà infine un’estesa trattazione dell’approccio quantomeccanico sviluppato per lo studio dei processi di Energy Transfer in ambiente complesso.
Nella seconda sezione sarà dapprima presentata l’applicazione dell’approccio precedentemente discusso a un sistema costituito da una coppia di cromofori identici (N-N’-dimetilperilene-3,4,9,10-dicarbossimmide, anche noto come PDI). Tale sistema fungerà da modello per un’esplorazione sistematica dell’effetto dell’ambiente sui processi di Energy Transfer. I dati così ottenuti serviranno quindi da guida per l’interpretazione dei risultati relativi a due complessi fotosintetici, la Peridinin-Chlorophyll-Protein (PCP) e la proteina Fenna-Matthews-Olson (FMO), su cui sarà ulteriormente testato il modello sviluppato. I risultati forniti dall’applicazione di quest’ultimo saranno infine messi a confronto con quelli ottenuti tramite modelli dipolari classici e ciò costituirà un’occasione per valutare i limiti validità di essi e le potenzialità legate a una trattazione quanto-meccanica dei processi di Energy Transfer in ambiente complesso.
6
Parte I
I modelli
7
Capitolo 1
Stati eccitati in soluzione
Da lungo tempo è noto che l’ambiente esercita una forte influenza sulla natura degli spettri elettronici di singole specie chimiche, in relazione sia ai fenomeni di assorbimento che a quelli di emissione. Sperimentalmente è possibile osservare, rispetto ai corrispondenti spettri registrati in vuoto, spostamenti dei massimi delle bande, variazioni di altezza e/o larghezza di queste ultime ed eventuale comparsa di nuove bande. In termini qualitativi e del tutto generali, tali fenomeni si spiegano alla luce della differente stabilizzazione relativa degli stati elettronici fondamentale ed eccitato del soluto; ciò è dovuto all’instaurarsi di un network di interazioni soluto-solvente (dispersive, elettrostatiche, legame a idrogeno, etc) più o meno favorevoli o sfavorevoli in relazione alla specifica natura chimica delle molecole interessate.
L’accurata modellizzazione della formazione e del rilassamento di stati eccitati in soluzione è un problema complesso. L’esigenza di accoppiare i processi di formazione e rilassamento dello stato elettronico eccitato del soluto con la dinamica delle molecole di solvente rende infatti necessario introdurre nei modelli il concetto di progressione temporale, concetto che può essere invece trascurato nella trattazione di gran parte delle proprietà e dei processi relativi al soluto nello stato fondamentale [12].
In questo contesto ci si limiterà alla presentazione dei processi di eccitazione elettronica trattati tramite l’uso del modello di solvatazione continuo PCM (Polarizable Continuum Model) [13]. In esso il solvente è descritto come un dielettrico continuo polarizzabile, caratterizzato dalla sua permittività dielettrica, e il soluto è rappresentato come una distribuzione di carica contenuta all’interno di una cavità ricavata nel dielettrico. Nelle sezioni seguenti il modello sarà presentato prima nella sua formulazione di base e poi in una formulazione estesa che permette di tenere conto degli effetti di solvatazione di non equilibrio caratteristici dei processi elettronici di tipo verticale.
Nell’ambito dei modelli di solvatazione continui, così come nel caso di molecole isolate, è uso calcolare le energie di eccitazione con due distinti approcci: i metodi di tipo State Specific (SS) e i metodi di tipo Linear Response (LR). Nei primi si risolve, generalmente con un approccio multireference (CI, MCSCF, CASSCF), l’equazione di Schrödinger non lineare per gli stati di interesse (fondamentale ed eccitato) e si postula che le energie di transizione siano date dalle differenze tra i corrispondenti valori del funzionale di energia libera. Nei secondi si evita invece il calcolo esplicito della funzione d’onda di stato eccitato e si determinano le energie di eccitazione come i poli di una funzione di risposta lineare frequenza-dipendente caratteristica del sistema molecolare nello stato fondamentale. E’ stato dimostrato che le due classi di metodi si equivalgono per molecole isolate (nel limite di soluzione esatta delle equazioni corrispondenti), ma differiscono sia da un punto di vista formale che da un punto di vista numerico per molecole trattate tramite modelli di solvatazione continui [14]. In questa sede ci limiteremo esclusivamente a una presentazione dei metodi di tipo Linear Response, in particolare dell’approccio TDDFT (Time Dependent Density Functional Theory) qui impiegato per il calcolo delle proprietà di transizione elettronica dei cromofori attivi nei processi di Energy Transfer.
8
1.1 Il modello di solvatazione PCM
Sarà di seguito presentato il modello di solvatazione continuo PCM (Polarizable Continuum Model). Prima di addentrarsi nei dettagli relativi alla sua formulazione, è opportuno ricordare che l’alternativa ai modelli di solvatazione continui è rappresentata dai modelli discreti. Mentre nei primi soltanto il soluto è trattato esplicitamente e il solvente è rimpiazzato da un dielettrico continuo, nei secondi si ricorre a una descrizione atomistica di tutte le componenti del sistema. Non è questa la sede per un confronto approfondito tra le due tipologie di approccio, tuttavia si osservi come l’uso di una descrizione continua permetta di evitare la considerazione di numerose differenti configurazioni soluto-solvente, in quanto viene implicitamente realizzata una media su di esse; ciò si traduce in un basso costo computazionale e questa caratteristica, unita alla facilità di accoppiamento tra i metodi quantomeccanici per la descrizione del soluto e i modelli continui per la trattazione della solvente, fa di questi ultimi uno strumento computazionale di larga ed efficace applicabilità.
Tornando ai modelli continui si osservi come in essi l’attenzione è focalizzata su una porzione del sistema complessivo, la quale viene isolata da tutto il resto per mezzo di una barriera fittizia. Nella fattispecie, nel modello PCM la molecola di soluto è inserita in una zona di spazio vuoto, chiamata cavità molecolare, e definita in modo da riprodurre il volume occupato dal soluto in esame ed escluso, pertanto, alle molecole di solvente. L’interazione tra il soluto e il mezzo solvente circostante viene poi “proiettata” sulla superficie della cavità molecolare; è dunque possibile individuare una quantità opportuna, vincolata sulla superficie, che riproduca in modo approssimato la risposta del mezzo solvente che si intende approssimare. Il sistema da trattare si riduce dunque a una molecola isolata interagente con una superficie: il metodo utilizzato per modellizzare questa interazione, ovvero per definire la “quantità opportuna” di cui sopra, è appunto il PCM.
1.1.1 Formulazione standard per gli stati d’equilibrio
Il solvente è descritto come un dielettrico continuo polarizzabile, caratterizzato dalla sua permittività dielettrica . Il soluto è rappresentato come una distribuzione di carica contenuta all’interno di una cavità ricavata nel dielettrico. Il problema elettrostatico risultante per il sistema soluto-solvente è determinato dall’equazione di Laplace-Poisson:
−∇[ ( )∇ ( )] = 4 ( ) (1.1) con le seguenti condizioni a contorno:
( ) = 1 ( ) =
9
dove è il vettore unitario perpendicolare alla superficie della cavità Γ, ed e indicano punti esterni (e) e interni (i) alla cavità. Nella formulazione generale del PCM, la polarizzazione del mezzo dielettrico è rappresentata dal potenziale di reazione del solvente ; esso è definito introducendo una densità di carica superficiale apparente sulla cavità:
( ⃗) = ∫ | ⃗ ⃗|( ⃗) (1.2)
(essendo ⃗ la coordinata di un generico punto interno alla cavità e ⃗ la coordinata di un generico punto sulla sua superficie). In tal modo, la sorgente del potenziale di reazione del solvente è ridotta a una distribuzione di carica limitata a una superficie chiusa: ciò implica una grande semplificazione rispetto ad altri metodi in cui l’intero volume del dielettrico è sorgente del potenziale di reazione. Il problema è poi ulteriormente semplificato facendo ricorso a un metodo BEM (Boundary Element Method), tramite il quale la superficie della cavità, costruita in termini di sfere sovrapposte centrate sugli atomi di soluto, è partizionata in N elementi finiti (tesserae) (vedi Fig. 1.1); ne consegue una discretizzazione della carica superficiale apparente in N cariche puntiformi ( ), ciascuna posta al centro della tessera corrispondente. Nel fare ciò, si assume che la densità di carica superficiale sia costante in ogni elemento di area : ( ⃗ ) = ( ⃗ ).
L’espressione per il potenziale di reazione del solvente assume dunque la forma:
( ⃗) = ∑ | ⃗ ⃗ |( ⃗ ) (1.3)
e l’interazione elettrostatica soluto-solvente può essere espressa come:
= ∑ ( ⃗ ) ( ⃗ ) (1.4) dove è il potenziale elettrostatico prodotto dal soluto sulla superficie della cavità.
Del modello PCM esistono diverse formulazioni, in ciascuna delle quali è data una definizione differente della densità di carica apparente . In particolare, nella versione IEFPCM (Integral Equation Formalism PCM) [15], a cui a partire da questo momento faremo riferimento, la carica superficiale apparente è ottenuta in termini di operatori integrali definiti sulla superficie della cavità e del potenziale del soluto sulla stessa superficie. Si rimanda al Rif. 15 per i dettagli della derivazione matematica e ci si limita a riportare qui l’equazione matriciale conclusiva dell’IEFPCM: ( ) = − (1.5)
Fig. 1.1
Visualizzazione di un esempio di cavità PCM: si noti la costruzione in termini di sfere sovrapposte centrate sugli atomi e la ripartizione della superficie in tesserae (vedi immagine schematica a lato).
10
dove: è una matrice quadrata (NxN) dipendente dalla geometria della cavità, dalla mesh della superficie e dalla permittività del solvente; è una matrice quadrata (NxN) dipendente dalla geometria della cavità e dalla mesh della superficie; è un vettore di dimensione N che contiene il potenziale elettrostatico prodotto dal soluto sugli elementi di superficie; è un vettore di dimensione N che contiene le cariche e che rappresenta l’effettiva incognita del problema.
Per applicare questa strategia a livelli di teoria quantomeccanici, nella fattispecie per risolvere l’equazione di Schrödinger effettiva per il soluto, l’idea di base è quella di definire un Hamiltoniano effettivo del soluto come somma di due termini: il primo è relativo alla molecola di soluto isolata, mentre il secondo descrive l’interazione elettrostatica soluto-solvente:
Ψ〉 = + Ψ〉 = |Ψ〉 (1.6) dove è l’autovalore energia interna del soluto. Poiché l’operatore di energia di interazione elettrostatica ha la forma = ∑ , appare subito evidente che la funzione d’onda del soluto (che determina la densità di carica ) dipende dall’operatore del solvente , il quale dipende a sua volta dalla funzione d’onda del soluto. In altri termini, il soluto e il solvente si polarizzano mutuamente: il problema deve essere pertanto risolto ricorrendo a una procedura iterativa che, se è l’operatore di Fock (o di Kohn-Sham) per il soluto isolato, si innesta sul problema SCF standard di determinazione della funzione d’onda del soluto.
Si osservi infine come, data la natura non lineare dell’Hamiltoniano effettivo del soluto, il principio variazionale può essere applicato ma non nella forma standard: il funzionale che deve essere minimizzato non corrisponde all’autovalore di energia interna , ma al funzionale di energia libera elettrostatica :
= Ψ Ψ
(1.7)
= Ψ Ψ −1
2 Ψ Ψ
Ciò corrisponde a sottrarre all’energia interna del soluto il lavoro di polarizzazione che quest’ultimo compie sul solvente e che è valutabile come la metà, cambiata di segno, dell’energia di interazione soluto-solvente.
1.1.2 Estensione agli stati di non-equilibrio
E’ noto che lo stato di arrivo nelle transizioni elettroniche di tipo verticale è uno stato di non-equilibrio. I moti nucleari sono infatti ordini di grandezza più lenti dei moti elettronici, per cui solo a tempi successivi rispetto all’istantanea variazione della distribuzione di carica elettronica del cromoforo si ha anche un rilassamento delle coordinate nucleari di quest’ultimo. Quando poi la transizione elettronica ha luogo in solvente, successivamente all’eccitazione del soluto si verifica anche un rilassamento dei gradi di libertà delle molecole di solvente attorno ad esso.
Il PCM può essere opportunamente esteso per descrivere gli effetti di solvatazione di non-equilibrio e trattare così la formazione e il rilassamento di stati eccitati in soluzione [16]. L’idea
11
chiave alla base di questa estensione è la separazione della polarizzazione del solvente in due componenti: una dinamica, associata al moto elettronico, e una inerziale, dovuta ai moti nucleari e molecolari. Si assume poi che, in seguito alla transizione elettronica verticale, la componente dinamica si equilibri istantaneamente rispetto allo stato finale del soluto e quella inerziale rimanga in equilibrio con lo stato iniziale. Tradotto in linguaggio PCM, ovvero in termini di cariche apparenti, ciò equivale a dire che:
( = 0) = = +
(1.8)
( → ∞) = = +
in cui si assume che l’eccitazione elettronica verso lo stato K avvenga all’istante iniziale = 0 e che a un tempo → ∞ lo stato eccitato sia completamente equilibrato (gli indici K e GS fanno riferimento, rispettivamente, allo stato eccitato e a quello fondamentale). La permittività del solvente è a sua volta suddivisa nelle sue componenti statica ( ) e ottica ( ); si ha che la polarizzazione inerziale dipende da entrambe, mentre quella dinamica solo dalla permittività ottica. In ultima analisi, le equazioni IEFPCM da risolvere per il soluto nello stato eccitato K sono:
( ) = −
(1.9)
( ) = −
dove è un vettore che contiene il potenziale elettrostatico del soluto nello stato eccitato K. Si noti infine che è possibile ricavare anche le cariche per semplice differenza (vedi eq. 1.8).
1.2 Metodi Linear Response
Nei metodi di tipo Linear Response (LR) le energie di eccitazione della specie chimica considerata sono determinate come i poli di funzioni di risposta lineare frequenza-dipendenti caratteristiche della specie nel suo stato elettronico fondamentale. Si riporta qui di seguito una sintetica presentazione di un esempio di approccio LR, la Time Dependent Density Functional Theory (TDDFT), che sarà impiegata nella successiva modellizzazione dei fenomeni di Energy Transfer.
1.2.1 TDDFT
Si consideri una qualsiasi specie chimica sottoposta a una perturbazione tempo-dipendente (per esempio, un campo elettromagnetico). La specie chimica è descritta dall’Hamiltoniano tempo-dipendente ( , ):
12
dove ( ) è l’Hamiltoniano del sistema isolato e ( , ) è un termine di generica perturbazione tempo-dipendente che guida l’evoluzione del sistema. Più nel dettaglio, ( , ) può essere scritto come somma di arbitrari operatori tempo-dipendenti di singola particella:
( , ) = ∑ ( , ) (1.11) Si ha che l’evoluzione temporale del sistema è completamente determinata dall’equazione di Schrödinger tempo-dipendente:
Ψ( , ) = Ψ( , ) (1.12)
Inoltre, in analogia con la derivazione delle equazioni di Kohn-Sham tempo-indipendenti proprie del metodo DFT, è possibile ricavare le corrispondenti equazioni tempo-dipendenti:
( , ) = ( , ) = ∑ | ( , )| (1.13a)
( , ) = ( , ) = − ∇ + ( , ) + ∫ | , |+ ( , )[ ] ( , ) (1.13b)
in cui: nella (1.13a) è l’esatta densità elettronica del sistema reale (ad elettroni interagenti), che si assume sia uguale alla densità del corrispondente sistema composto di elettroni non interagenti (la funzione d’onda elettronica che descrive quest’ultimo è un singolo determinante di Slater costruito con gli N spin-orbitali di più bassa energia); nella (1.13b) l’operatore monoelettronico di Kohn-Sham contiene, nell’ordine: l’energia cinetica del sistema non interagente, il potenziale di interazione nuclei-elettrone, il potenziale Coulombiano e il potenziale di scambio e correlazione. Da notare che nella (1.13b) è stata applicata l’approssimazione adiabatica (Adiabatic Local Density Approximation, ALDA), ovvero il funzionale di scambio e correlazione [ ] dipende da una densità definita a un tempo fissato.
A partire dalle equazioni sopra riportate riscritte in un’opportuna base atomica si perviene, tramite un adeguato trattamento matematico in cui la variazione della densità elettronica conseguente all’applicazione della perturbazione è troncata al 1° ordine, al seguente autosistema:
∗ ∗ = 10 −10 (1.14)
i cui autovalori (che costituiscono anche i poli della funzione di risposta lineare) sono le energie di eccitazione cercate. Gli elementi delle matrici A e B sono sono definiti in termini degli orbitali di Kohn-Sham e delle relative energie orbitaliche :
, = ( − ) − , (1.15)
, = − ,
essendo , un generico integrale bielettronico:
13
Nell’indicizzazione degli orbitali è stata adottata la convenzione consueta: (i, j, k…) per gli orbitali occupati; (a, b, c,…) per quelli virtuali. Infine, gli autovettori ( ) contengono gli elementi della matrice di risposta lineare nella base degli orbitali molecolari imperturbati e descrivono la densità di transizione al 1° ordine di ciascuna eccitazione.
1.2.2 Uso dell’IEFPCM nel metodo TDDFT
Generalizzando la teoria della risposta lineare ai sistemi molecolari in fase condensata, le energie di eccitazione del soluto possono essere determinate, al solito, come i poli della funzione di risposta lineare, cioè in pratica risolvendo l’autosistema non-Hermitiano:
∗ ∗ = 1 0
0 −1 (1.17) Tale autosistema è formalmente identico a quello riportato nell’eq. 1.14. Tuttavia, in questo caso la definizione degli elementi delle matrici A e B è differente:
, = ( − ) − , + ,
(1.18) , = − , + ,
Nelle definizioni sopra riportate è infatti contenuto l’effetto del solvente, che si esplica in due modi: indirettamente attraverso il termine , , definito in termini degli orbitali molecolari e
delle corrispondenti energie orbitaliche soluzioni delle equazioni di Kohn-Sham contenenti il campo di reazione del solvente (vedi eq. 1.16), ed esplicitamente attraverso il termine di perturbazione , . Quest’ultimo può essere trattato come l’interazione elettrostatica tra la
distribuzione di carica ∗ e il contributo dinamico al potenziale di reazione del solvente indotto dalla distribuzione di carica ∗ ; e può essere scritto in termini del prodotto vettore tra il potenziale elettrostatico e le cariche apparenti dinamiche, determinati dalle corrispondenti densità di transizione:
, = ∑ ∫ ⃗ ∗( ⃗) ( ⃗)| ⃗ ⃗ | ⃗ ; , ∗ (1.19)
Si noti che che in questo caso è necessario utilizzare, al posto della permittività dielettrica statica, la permittività dielettrica dinamica valutata alla frequenza della transizione considerata.
14
Capitolo 2
Il modello per il metallo
Come ben noto, l’interazione tra gli elettroni di conduzione di un campione di materiale metallico (di dimensioni microscopiche o macroscopiche) e un campo elettromagnetico esterno causa l’oscillazione di tali elettroni alla frequenza plasmonica caratteristica del campione metallico in esame. Affinchè ciò si verifichi, deve essere soddisfatta la condizione di risonanza: la radiazione di frequenza inferiore a quella plasmonica è infatti riflessa (perché gli elettroni nel metallo schermano il campo elettrico della luce), mentre quella di frequenza superiore è trasmessa (perché gli elettroni non possono rispondere abbastanza velocemente da schermarla). Per la maggior parte dei metalli la frequenza plasmonica cade nella regione dell’ultravioletto; ciò fa sì che essi riflettano nella regione del visibile e determina i loro caratteristici colori metallici.
Quando poi l’aggregato metallico ha dimensioni nanometriche, gli elettroni risultano “intrappolati” all’interno della nanoparticella e i loro moti sono limitati alla superficie di quest’ultima: il metallo diventa così colorato. Più precisamente, la frequenza ed intensità delle bande plasmoniche di assorbimento sono caratteristiche del tipo di materiale e sono altamente sensibili alla dimensione e alla forma delle nanostrutture, nonchè all’ambiente che circonda queste ultime. Per esempio, è proprio alla presenza di particelle metalliche colloidali che si devono i colori sgargianti delle vetrate d’epoca delle chiese.
In questo capitolo, sarà presentata una breve trattazione delle proprietà plasmoniche dei metalli. Ci si soffermerà in particolare sul comportamento plasmonico di aggregati di dimensioni nanometriche (nanoparticelle) e sulle loro applicazioni nell’ambito delle cosiddette “Surface Enhanced Spectroscopies”. Sarà inoltre descritto il ruolo di tali particelle metalliche come accettori nei processi di Energy Transfer e, più in generale, la loro influenza sui processi di decadimento di molecole eccitate. Infine, sarà presentato per le nanoparticelle metalliche un modello continuo di tipo PCM, nell’ambito del quale sarà possibile calcolare le quantità fisiche caratteristiche dei processi precedentemente descritti.
Fig. 2.1
I colori delle vetrate delle chiese si devono alla presenza nella matrice vetrosa di nanoparticelle colloidali di metalli preziosi (oro, argento).
15
2.1 Proprietà plasmoniche
I plasmoni di superficie, conosciuti anche come polaritoni plasmonici di superficie, sono onde elettromagnetiche che si propagano in direzione parallela all’interfaccia metallo/dielettrico (o metallo/vuoto). Dal momento che l’onda viaggia al confine tra il metallo e il mezzo esterno, queste oscillazioni sono molto sensibili a qualsiasi cambiamento di tale confine: per esempio il fenomeno è sfruttato in numerosi strumenti standard per la misurazione dell’adsorbimento di materiale su superfici metalliche.
L’eccitazione del plasmone di superficie per mezzo della radiazione viene descritta come una risonanza plasmonica di superficie (SPR, Surface Plasmon Resonance) per le superfici planari (vedi Fig. 2.2) o risonanza plasmonica di superficie localizzata (LSPR, Localized Surface Plasmon Resonance) per le strutture metalliche di dimensioni nanometriche (vedi Fig.2.3).
Sperimentalmente, l’interazione delle nanoparticelle metalliche con la radiazione è messa in evidenza attraverso fenomeni di assorbimento e scattering: i primi sono responsabili del colore percepito, mentre i secondi sono impiegati per l’osservazione delle nanoparticelle tramite tecniche di microscopia. Da un punto di vista teorico, l’esistenza e le proprietà dei plasmoni di superficie possono essere descritti con vari modelli, tuttavia il modo forse più semplice è quello di trattare ogni materiale come un continuo omogeneo, descritto da una permittività dielettrica che
Fig. 2.2
All’interfaccia metallo-dielettrico si creano cariche di polarizzazione. Gli elettroni nel metallo rispondono a tale polarizzazione dando origine a un modo plasmonico di superficie, che si propaga nelle direzioni x e y lungo l’interfaccia tra i due materiali e decade rapidamente nella direzione z.
Metal Surface
Metal Nanoparticle
Fig. 2.3Le dimensioni delle nanoparticelle metalliche sono molto inferiori rispetto alla lunghezza d’onda della radiazione incidente. Ciò fa sì che il plasmone oscilli localmente attorno alla nanoparticella a una frequenza nota come Localized Surface Plasmon Resonance (LSPR).
16
è valutata come complessa. Affinchè i termini che descrivono i plasmoni di superficie esistano, la parte reale della costante dielettrica del metallo deve essere negativa e la sua grandezza deve essere superiore a quella del dielettrico. In particolare, per l’interfaccia aria/metallo questa condizione è soddisfatta nella regione dell’infrarosso-visibile.
I fenomeni di risonanza plasmonica di superficie sono comunemente impiegati per migliorare la sensibilità in diverse misure spettroscopiche, tra cui la fluorescenza, l’assorbimento IR e il Raman scattering [17]. Infatti, i modi plasmonici di superficie, che possono anche essere visti come eccitazioni collettive del gas elettronico confinate all’interno della nanoparticella, sono caratterizzati da multipoli di transizione insolitamente grandi e sono dunque in grado di amplificare i fenomeni coinvolgenti campi elettromagnetici. Un possibile modello per la descrizione di tali effetti è costituito dalla cosiddetta Discrete Dipole Approximation (DDA) [18], in cui le nanoparticelle sono discretizzate in termini di un numero N di dipoli puntiformi polarizzabili interagenti con un’onda piana monocromatica incidente da una distanza infinita: si valutano così le proprietà di assorbimento e scattering di nanoparticelle di differente forma e dimensione, nonché gli effetti di amplificazione del campo elettrico locale indotti dalla presenza di queste ultime (vedi Fig. 2.4).
Soprattutto gli esperimenti di scattering Raman hanno tratto notevole impulso dalla possibilità di generare intensi campi elettrici locali tramite eccitazione dei modi plasmonici localizzati sulla superficie di nanoparticelle metalliche. In condizioni normali lo scattering Raman è infatti di decine di ordini di grandezza meno intenso della fluorescenza ed è pertanto molto difficile applicare tale tecnica a molecole singole. Ciò diventa però possibile tramite ricorso alla sua variante nota come Surface Enhanced Raman Scattering (SERS): in essa infatti l’intensità Raman della molecola risulta amplificata, grazie all’enhancement del campo elettrico locale dovuto alla presenza di nanoparticelle metalliche, di diversi ordini di grandezza rispetto alla corrispondente intensità della molecola isolata :
= | | (2.1)
Ai fini dell’ottimizzazione dei fenomeni di enhancement sopra descritti, è fondamentale la creazione dei cosiddetti hot spots, ovvero zone di localizzazione del campo elettrico che possono essere prodotte tramite costruzione di reticoli regolari di nanoparticelle oppure tramite l’impiego di superfici con caratteristiche frattali. A tal riguardo, esiste una nutrita letteratura avente per oggetto la comprensione del legame tra proprietà strutturali dei nanoaggregati ed entità di
Fig. 2.4
Proprietà ottiche di nanoparticelle di argento ottenute con calcoli DDA: a sinistra, spettri di estinzione di nanoparticelle di differenti forme (tutte con lo stesso volume di una sfera di R=50Å); in alto, contorni del campo elettrico locale (| | ) per particelle, nell’ordine, sferiche, cubiche e tetraedriche.
17
amplificazione dei campi elettrici locali e quindi, in ultima analisi, dei segnali Raman misurati [19,20].
Le nanoparticelle metalliche trovano inoltre crescente applicazione anche in campo biologico e biomedico. Il loro impiego presenta infatti molteplici vantaggi, tra cui la facilità di coniugazione a proteine specifiche, l’attività ottica a lunghezze d’onda biocompatibili, la stabilità chimica e fotochimica, la non tossicità verso i tessuti (quest’ultima caratteristica in relazione all’oro). Tali nanoparticelle possono essere quindi proficuamente impiegate in esperimenti di sensing, ovvero per la rilevazione di qualunque tipo di fenomeno (cambiamenti nel materiale di supporto, legame covalente di molecole, formazione di dimeri, etc) che influenzi la frequenza di risonanza plasmonica delle nanoparticelle stesse. Infine, esse sono anche utilizzate nella terapia fototermica dei tumori: è infatti possibile preparare speciali nanostrutture con picchi di risonanza plasmonica alla frequenza desiderata, in modo che esse agiscano da sistemi di trasporto del calore impiegato per il danneggiamento e la distruzione delle cellule tumorali.
2.1.2 Effetto delle nanoparticelle metalliche sui processi fotofisici
Si consideri un sistema costituito da una molecola posta in prossimità di un aggregato metallico di dimensioni nanometriche. Si assuma che un campo elettromagnetico incida sul sistema, eccitando così i modi plasmonici superficiali della nanoparticella metallica. Questi ultimi possono generare, a loro volta, un campo elettrico evanescente e di alta intensità in prossimità della superficie stessa: pertanto una molecola posta sulla superficie del corpo metallico risentirà, oltrechè del campo incidente, anche del campo amplificato dal metallo e dunque le sue proprietà di risposta elettrica subiranno una notevole variazione. Nella fattispecie, i fenomeni di assorbimento e di decadimento radiativo della molecola risulteranno amplificati; inoltre, al canale di decadimento non radiativo proprio della molecola isolata si affiancherà un ulteriore canale di decadimento non radiativo, consistente quest’ultimo nell’Excitation Energy Transfer dalla molecola eccitata alla nanoparticella metallica. L’effetto netto della presenza del metallo dipenderà da quale dei due processi risulta privilegiato e potrà consistere tanto in un’amplificazione (enhancement) quanto in una diminuzione (quenching) della luminescenza della molecola rispetto al caso in assenza di metallo. I processi fin qui discussi sono ben riassunti negli schemi riportati in Fig. 2.5-2.6 [17].
Fig. 2.5
Schema dei processi fotofisici attivi in un sistema costituito da una molecola isolata: assorbimento ( =sezione d’urto), conversione interna ( ), decadimento radiativo ( ), decadimento non radiativo della molecola isolata ( ) (tra parentesi, le relative costanti cinetiche).
Fig. 2.6
Schema dei processi fotofisici attivi in un sistema costituito da una molecola più una nanoparticella metallica: ai processi riportati in Fig. 2.5 si aggiunge il decadimento non radiativo verso il metallo ( ). | ( , )| e | ( , )| rappresentano l’amplificazione del campo elettrico rispettivamente alla frequenza di incidenza e a quella di emissione .
18
2.2 Il modello IEFPCM per il metallo
In questa sezione sarà presentato un modello per il calcolo delle costanti di decadimento radiativo e non radiativo di una molecola posta nelle vicinanze di una nanoparticella metallica di forma arbitaria. La modellizzazione dei fenomeni di enhancement e quenching della fluorescenza riveste infatti grande importanza, in quanto tali fenomeni sono sfruttati in numerose applicazioni tecnologiche, tra cui quelle basate sull’uso dei processi di Energy Transfer.
Il modello qui illustrato [21,22] è fondato su un principio gerarchico: la parte principale del sistema oggetto di studio è descritta a un elevato livello di accuratezza, mentre le porzioni rimanenti sono trattate considerando soltanto le caratteristiche decisive ai fini dell’interazione con la parte principale. Pertanto la molecola, che nei fenomeni studiati gioca il ruolo più importante, è descritta a un livello di teoria quantomeccanico; il metallo è invece trattato, sfruttando il metodo PCM (presentato nella sezione 1.1), come un corpo continuo caratterizzato dalle sue proprietà di risposta ai campi elettrici (sia quelli esterni che quelli generati dalla distribuzione di carica molecolare). In quanto finora esposto risiedono due aspetti di novità del presente modello rispetto ad altri precedentemente impiegati: in primo luogo, nella descrizione della molecola non si ricorre all’approssimazione di dipolo puntiforme polarizzabile (che potrebbe essere non giustificata specie nel caso di piccole distanze metallo-molecola), bensì viene impiegato un trattamento di tipo quantomeccanico; in secondo luogo, è possibile considerare particelle metalliche di forma complessa, anziché soltanto forme regolari come per esempio superfici planari infinite e sfere, senza che sia peraltro necessario assumere per il metallo una risposta di tipo dipolare.
Più nel dettaglio, la nanoparticella metallica è costruita come una particella PCM, ovvero tramite l’intersezione di un opportuno numero di superfici sferiche di raggio e posizione arbitrari (vedi Fig. 2.7). Per descrivere più adeguatamente il sistema sperimentale, può inoltre essere utile inserire molecola e metallo in un contesto di solvatazione: in esso il solvente è anch’esso descritto secondo il modello PCM, per cui si rende necessario considerare l’ulteriore superficie della cavità molecolare.
Nel considerare la risposta complessiva del sistema ai campi elettromagnetici, è possibile limitare la trattazione ai soli effetti del campo elettrico. Inoltre, anche limitandosi al campo elettrico, risulta più semplice e immediato descrivere il sistema nell’approssimazione quasistatica, anziché ricorrere alla trattazione completamente elettrodinamica: cioè è però possibile soltanto nel caso
Fig. 2.7
La nanoparticella metallica di forma complessa è descritta come una particella PCM, ovvero tramite intersezione di più superfici sferiche.
19
in cui le dimensioni degli oggetti considerati siano inferiori alla lunghezza d’onda del campo elettrodinamico. In pratica, la risposta del metallo ai campi elettrici viene descritta sotto l’assunzione che esso si comporti da conduttore perfetto (permittività reale e infinita) se soggetto a campi statici, e da dielettrico (permittività complessa e finita) se soggetto a campi dinamici. In quest’ultimo caso, è impiegata per la permittività frequenza-dipendente una definizione semiempirica: essa si ottiene partendo dall’espressione ricavata nel modello di Drude per elettroni liberi [23] e correggendola per introdurre gli effetti “Quantum Size” (in pratica, per tenere conto del ridotto cammino libero dell’elettrone nella nanoparticella) e la distinzione tra elettroni liberi e legati. Alla fine si ricava per la permittività frequenza-dipendente la seguente definizione [24] :
( ) = ( ) + Ω − (2.2)
dove è il raggio della nanoparticella e i valori per la permittività di bulk e per i parametri caratteristici del metallo (Ω , frequenza di plasma del metallo; , tempo di rilassamento; , velocità di Fermi) possono essere ricavati sfruttando i dati sperimentali (vedi Tabella 2.1).
Nell’ambito di questo modello, l’interazione di stato fondamentale tra la molecola e il metallo è di natura elettrostatica ed dovuta alla loro mutua polarizzazione. Più nel dettaglio, la molecola è descritta da un Hamiltoniano effettivo ottenuto sommando all’Hamiltoniano della molecola isolata un termine di energia di interazione elettrostatica tra la densità di carica della molecola (nuclei + elettroni) e la polarizzazione del metallo indotta dalla densità di carica molecolare stessa. Tale polarizzazione è convenientemente espressa in termini delle cariche apparenti poste sulla superficie della particella metallica (e sulla superficie della cavità molecolare nel caso in cui sia presente anche il solvente):
( , ) = ∑ ( ; , ) ( ; ) (2.3) Al solito, le cariche apparenti sono ottenute risolvendo le equazioni PCM tramite ricorso a un metodo BEM (Boundary Element Method) (vedi sezione 1.1). Nello specifico, vengono tessellate tutte le interfacce presenti: tanto la superficie della particella metallica quanto la superficie della cavità molecolare per il caso in presenza di solvente, mentre soltanto la superficie della particella metallica per il caso in vuoto. Più nel dettaglio, per il problema di stato fondamentale, ove entra in gioco l’interazione con campi statici per i quali il comportamento del metallo viene assimilato a quello di un conduttore perfetto ( → ∞), si ricorre alla normale trattazione IEF e l’equazione da risolvere è del tipo:
= − (2.4) Ω
Oro 0.293 306 0.64
Argento 0.332 1320 0.64
Tabella 2.1
Parametri caratteristici dei metalli (Au, Ag), riportatati in unità atomiche.
20
(vedi, per confronto, 1.5). Essa poteva essere ricavata anche da considerazioni sulle condizioni a contorno di un conduttore perfetto e deriva essenzialmente dal fatto che la distribuzione di carica che si genera sulla superficie della particella metallica è tale da impedire al campo esterno di penetrarvi. Meno immediato da trattare è invece il caso in cui è di natura complessa: in tal caso, l’equazione generale per il calcolo delle cariche PCM alle diverse interfacce, espressa per comodità secondo il formalismo dell’IEF, risulta (vedi per confronto eq. 1.5):
[ − (1 2⁄ ) ] = −[ − (1 2⁄ ) ] (2.5)
dove è una matrice diagonale di elementi:
= se ∈ interfaccia metallo-vuoto (2.6)
= se ∈ interfaccia solvente-vuoto (2.7)
= se ∈ interfaccia metallo-solvente (2.8)
e dove e sono, rispettivamente, le costanti dielettriche del metallo e del solvente. Si noti infine che la procedura adottata per la generazione della tessellazione cambia a seconda che le tessere appartengano alla superficie della cavità molecolare o a quella della particella metallica. Per quanto riguarda le prime, la procedura utilizzata è quella classica del PCM, consistente nell’uso di superfici sferiche di raggio opportuno centrate ciascuna su un atomo del sistema e suddivise in tessere triangolari di uguale area a partire dai vertici di un poligono regolare inscritto in esse. Per quanto riguarda, invece, le seconde, è comodo, ai fini dell’implementazione, sfruttare lo stesso tipo di algoritmi già impiegati per la trattazione della cavità molecolare; tuttavia, i due processi di generazione non possono seguire procedure identiche, date le dimensioni generalmente non comparabili dei due corrispondenti sistemi (molecola e metallo). Non è infatti possibile generare lo stesso numero di tessere per le sfere molecolari (di raggio mediamente compreso tra 1Å e 2Å) e per quelle metalliche (di raggio variabile, ma comunque compreso tra i 10Å e i 500Å): infatti o verrebbero generate troppe tessere oppure l’area delle tessere metalliche risultanti risulterebbe troppo grande per fornire una descrizione adeguata. D’altra parte, però, non è nemmeno necessario utilizzare una tessellazione uniforme della superficie metallica, in quanto la porzione di sistema di maggior interesse, per la quale quindi è più importante avere una descrizione dettagliata, è solo quella in stretta prossimità della molecola. Pertanto, per la generazione della tessellazione della superficie metallica, si utilizza un algoritmo consistente nella produzione di una tessellazione triangolare uniforme, che viene poi successivamente raffinata, secondo un criterio prestabilito, solo per le tessere vicine agli atomi della molecola in esame (vedi Fig. 2.8).
Fig. 2.8
Raffinamento della tessellazione della superficie metallica nella zona vicina alla molecola.
21
2.2.1 Estensione del modello alla trattazione degli stati eccitati
Le energie di eccitazione elettronica e le densità di transizione della molecola sono calcolate con un approccio di tipo Linear Response [Time Dependent Hartree-Fock (TD-HF), Time Dependent Density Functional Theory (TD-DFT), ma anche metodi semiempirici (come ZINDO) che si può assumere siano basati su una funzione di risposta approssimata]. In questo caso, nell’equazione della funzione di risposta che determina le energie di eccitazione e le densità di transizione della molecola, si aggiunge un termine che rappresenta l’interazione della densità di transizione con la polarizzazione oscillante del metallo (e del solvente) indotta dalla densità di transizione stessa (vedi, per confronto, eq. 1.14-1.16):
A B
B∗ A∗ − 10 −10 XY = 0 (2.9)
, = ( − ) + , + , ( )
(2.10) , = , + , ( )
Questa interazione è descritta con la procedura IEF-BEM già presentata per l’Hamiltoniano di stato fondamentale; in questo caso, tuttavia, è impiegata per il metallo (e per il solvente) una permittività frequenza-dipendente (con frequenza scelta così da essere uguale a quella della transizione elettronica molecolare studiata):
, = ∑ ∫ ⃗ ∗( ⃗) ( ⃗)| ⃗ ⃗ | ⃗ ; ( ), ∗ (2.11)
Nell’equazione sopra riportata, le sono le cariche apparenti dovute alla polarizzazione del metallo indotta dalla densità di transizione (si veda, per confronto, l’eq. 1.19). Poiché per il metallo la permittività frequenza-dipendente è generalmente complessa, i poli della funzione di risposta sono a loro volta complessi: più nel dettaglio, la loro parte reale fornisce le energie di eccitazione, mentre quella immaginaria è legata all’inverso del tempo di vita non radiativo dello stato eccitato molecolare dovuto all’Excitation Energy Transfer al metallo (e alla conseguente dissipazione di energia). Poiché la velocità di decadimento non radiativo Γ può essere scritta come l’inverso del tempo di vita, si ha che:
Γ = −2Im{ } = −
ℏ∑ Im ( ⃗ ; , ) ( ⃗ ) (2.12)
dove è il potenziale elettrostatico generato dalla densità associata alla transizione dallo stato fondamentale allo stato eccitato K, e le sono, come già detto, le cariche apparenti dovute alla polarizzazione del metallo indotta dalla densità di transizione stessa.
Accanto al decadimento non radiativo, un’altra modalità di dissipazione dell’energia di eccitazione molecolare è quella radiativa: la molecola nello stato eccitato di interesse può cioè andare incontro al processo di fluorescenza. Nell’ambito del presente modello, è stata messa appunto una metodologia tale per cui i tempi di vita radiativi sono calcolati in modo coerente rispetto ai tempi di vita non radiativi, considerando esplicitamente la presenza del metallo (e del solvente)
22
attorno alla molecola. Più nel dettaglio, la velocità di decadimento radiativo della molecola è data dalla seguente espressione:
Γ =
ℏ | ⃗ | (2.13)
dove ⃗ è il dipolo di transizione tra lo stato fondamentale e lo stato eccitato K e è l’indice di rifrazione del mezzo in cui l’emissione ha luogo. Il dipolo di transizione può essere scritto come: ⃗ = ⃗ + ⃗ + ⃗ (2.14) Infatti, l’interazione con il metallo (e con il solvente), oltre a modificare direttamente il dipolo di transizione molecolare ⃗ , dà anche origine a dei termini espliciti costituiti dai dipoli indotti sul metallo (e sul solvente) dalla densità di transizione molecolare.
In particolare, l’interazione tra il dipolo indotto sul metallo (o sul solvente) dalla densità di transizione molecolare e il campo esterno ⃗ può essere riscritta in termini dell’interazione tra la carica di polarizzazione indotta sul metallo (o sul solvente) dal campo esterno e il potenziale elettrostatico prodotto dalla transizione molecolare:
− ⃗ ∙ ⃗ = (2.15) Pertanto, la componente -esima del dipolo indotto sul metallo può essere ricavata come:
[ ⃗ ] = − ∑ ( ⃗ ) ( ⃗ ) (2.16)
La conoscenza del dipolo indotto sul metallo dalla transizione molecolare serve anche ai fini del calcolo del coefficiente di assorbimento , che viene valutato come:
= ℏ | ⃗ | (2.17)
Inoltre, è anche possibile calcolare la risposta della particella metallica isolata al campo esterno. Infatti gli elementi del tensore polarizzabilità del metallo possono essere scritti come:
= (2.18)
dove e sono le componenti, rispettivamente, del dipolo elettrico indotto sulla particella metallica e del campo elettrico esterno agente sulla particella stessa. Il dipolo indotto può essere espresso in termini di un set di cariche apparenti come:
⃗ = ∑ ∈ ⃗ = ⃗ (2.19) dove la somma corre soltanto sulle tessere appartenenti alla superficie metallica e la serie di vettori ⃗ contiene le posizioni delle rispettive tessere. In definitiva, gli elementi del tensore polarizzabilità del metallo possono essere ottenuti come:
23
= ( ) (2.20)
dove si è voluta sottolineare la dipendenza delle cariche apparenti dalla costante dielettrica frequenza-dipendente del metallo . Poiché tale costante è generalmente complessa, anche il tensore polarizzabilità del metallo sarà complesso; in particolare, la conoscenza della sua componente immaginaria permette di calcolare la sezione d’urto frequenza-dipendente della nanoparticella, cioè in pratica di ricostruire il suo spettro plasmonico:
( ) = 4 Im〈 ( )〉 (2.21)
Infine, si osservi che le quantità fin qui discusse possono essere tra loro combinate per ottenere degli opportuni indici che riassumano l’effetto delle nanoparticelle metalliche sul processo di fluorescenza, ovvero che forniscano una misura del quenching o dell’enhancement di quest’ultima. Tali indici sono la resa quantica di fluorescenza Φ :
Φ = (2.22)
che è definita come il rapporto tra il numero di fotoni emessi e il numero di fotoni assorbiti e rappresenta l’efficienza di fluorescenza ad intensità di assorbimento costante (si noti che nell’eq. 2.22 sono stati trascurati eventuali canali di decadimento non radiativo Γ propri della molecola isolata); e la Relative Brightness di fluorescenza Φ :
Φ = Φ (2.23)
che è sostanzialmente la resa quantica corretta per tenere conto della differenza di popolazione nello stato eccitato causata dagli effetti del metallo sul coefficiente di assorbimento molecolare: se, per esempio, il metallo incrementa l’assorbimento, un numero maggiore di molecole sarà presente nello stato eccitato e sarà dunque disponibile per l’emissione. La Relative Brightness è pertanto utile per quantificare l’enhancement o il quenching della fluorescenza indotto dal metallo ad intensità di eccitazione costante: in particolare, se Φ > 1, c’è enhancement.
24
Capitolo 3
Energy Transfer in ambienti complessi
L’Electronic Energy Transfer (EET) è un processo in cui l’energia di eccitazione di un cromoforo “donatore” è trasferita a un cromoforo “accettore” in seguito a un’interazione tra i due. Tale fenomeno è stato ed è tuttora oggetto di numerose indagini, sia sperimentali che teoriche: la comprensione dei meccanismi microscopici alla base dell’EET è infatti di fondamentale importanza ai fini dell’ottimizzazione delle numerose applicazioni basate su tale processo.
La principale teoria che pone in relazione quantità sperimentali con i meccanismi dell’EET fu formulata da Förster [11] nel 1948 ed è ampiamente usata ancora oggi. Essa assume che il coupling elettronico tra i cromofori sia di natura esclusivamente coulombiana e che sia approssimabile in termini di un’interazione dipolo-dipolo tra i dipoli di transizione associati alle molecole di donatore e accettore. In conseguenza di tale approssimazione, la teoria di Förster prevede per la costante di velocità di EET una dipendenza dalla distanza di tipo 1⁄ , dove è la distanza tra i centri di massa della coppia di cromofori. Peraltro si noti che per distanze corte, a cui è possibile una sovrapposizione diretta tra le funzioni d’onda elettroniche di donatore e accettore, l’Energy Transfer si realizza attraverso interazioni di scambio piuttosto che coulombiane: tale meccanismo è stato elucidato da Dexter [25] e prevede una dipendenza dalla distanza di tipo esponenziale.
I limiti principali della teoria di Förster emergono nelle situazioni in cui l’approssimazione dipolare non è giustificabile (per esempio, per cromofori strettamente vicini contenuti in una matrice proteica o altro mezzo) o in cui una (o entrambe) le transizioni elettroniche coinvolte sono proibite per simmetria: la teoria di Förster trascura infatti completamente il contributo degli stati “dark”, poiché i relativi dipoli di transizione sono pressochè nulli.
Inoltre, si consideri che in molti sistemi fotosintetici i pigmenti attivi nell’Energy Transfer sono così densamente impaccati da implicare una delocalizzazione dei relativi stati eccitati. In generale, il grado di delocalizzazione è dettato dall’entità del coupling elettronico tra i cromofori ed è a sua volta responsabile del tipo di dinamica secondo cui l’Energy Transfer procede. Nella fattispecie, la teoria di Förster è formulata nel limite di coupling debole, sotto l’assunzione che l’energia di eccitazione sia trasferita tra cromofori già in equilibrio con l’ambiente; tale tipo di trasferimento è chiamato incoerente ed in esso il moto eccitonico procede diffusivamente secondo uno schema di tipo “random walk”, con eccitazione localizzata su un singolo cromoforo alla volta. Il caso opposto è quello di coupling forte: il corrispondente tipo di trasferimento è detto coerente ed è caratterizzato da eccitazione delocalizzata su più cromofori allo stesso tempo. Sono infine possibili regimi di tipo intermedio, in cui il coupling elettronico tra cromofori e l’interazione con l’ambiente hanno peso comparabile [26,27].
Un ulteriore aspetto decisamente rilevante ai fini della corretta modellizzazione dei fenomeni di Energy Transfer è rappresentato dalla comprensione dell’effetto dell’ambiente su di essi [28]. In questo punto risiede un altro grosso limite del modello di Förster, il quale – come si vedrà – affronta il problema tramite introduzione di un semplice fattore di screening costante rispetto alla distanza e all’orientazione relativa di donatore e accettore.
25
Alla luce di quanto finora esposto, appare più che mai evidente l’esigenza di modelli alternativi, che permettano da un lato di superare l’approssimazione dipolare tramite descrizioni più accurate dei cromofori interagenti, dall’altro di trattare opportunamente l’effetto dell’ambiente sull’entità dei coupling elettronici. In particolare, in questo capitolo sarà presentato un modello quantomeccanico di tipo IEFPCM-TDDFT [29]: esso coniuga una trattazione Linear Response delle proprietà di transizione elettronica dei cromofori con una descrizione dell’ambiente in termini del modello PCM. Per ambiente si intende qui un intorno complesso, costituito da diverse componenti: mezzo solvente, matrice proteica, nanoparticelle metalliche, etc. Nel seguito sarà illustrato come tali componenti vengono modellate e in che modo esse esercitano il loro effetto sui fenomeni di Energy Transfer. Prima dell’esposizione del modello quantomeccanico, sarà però brevemente presentata la teoria di Förster, la quale, pur nell’ambito dei suoi limiti di validità, continua a costituire un punto di riferimento imprescindibile per gran parte degli studi del settore.
3.1 Il modello di Förster
Si consideri un sistema donatore-accettore (D-A), in cui il donatore è nello stato eccitato e l’accettore è nello stato fondamentale. Al fine di descrivere l’Excitation Energy Transfer in tale sistema, si introducano delle funzioni d’onda indipendenti per ciascuna molecola, definite – in base all’approssimazione di Born-Oppenheimer – come il prodotto di una funzione d’onda elettronica per una funzione d’onda nucleare: Ψ ( ; ) = ( ; ) ( ) ( = o ; = (ground, ) o (excited, ); con e , rispettivamente, coordinate elettroniche e nucleari). I livelli vibrazionali di energia associati agli stati fondamentale ed eccitato sono indicati, rispettivamente, con e .
Lo stato iniziale in cui l’eccitazione è localizzata sul donatore è rappresentato dalla funzione | 〉 = |Ψ 〉|Ψ 〉 ed è caratterizzato dall’energia + . In modo analogo, lo stato finale è dato dalla funzione | 〉 = |Ψ 〉|Ψ 〉 e possiede l’energia + . Le energie di transizione → sono esprimibili in termini della differenza: + −
− . Come già ricordato, l’Energy Transfer procede tramite diseccitazione del donatore e simultanea eccitazione dell’accettore, conseguente all’interazione tra di essi. Poichè la teoria di Förster assume che il sistema D-A sia in equilibrio termico con l’ambiente, la velocità di transizione dallo stato iniziale | 〉 allo stato finale | 〉 può essere calcolata usando la regola d’oro di Fermi:
=
ℏ ∑ ∑ × Ψ , Ψ Ψ , Ψ ×
(3.1)
+ − −
Nell’espressione sopra riportata, la distribuzione termica per gli stati vibrazionali iniziali del donatore e dell’accettore è denotata, rispettivamente, da e . L’operatore tiene conto delle interazioni coulombiane tra donatore e accettore. Sotto l’assunzione che gli elementi della matrice di accoppiamento elettronico ( ) siano indipendenti dalle coordinate nucleari (approssimazione di Condon), si può scrivere la seguente espressione semplificata:
26
Ψ , Ψ Ψ , Ψ = (3.2)
Per un sistema D-A neutro, la componente dipolare domina le interazioni coulombiane. Pertanto, in questo caso, è dato semplicemente da:
= ⃗
( ) ⃗( )
(3.3)
dove è la distanza D-A e è un fattore geometrico adimensionale determinato dall’orientazione spaziale dei dipoli di transizione del donatore e dell’accettore ⃗( ) = ̂ .
Nella teoria di Förster, la velocità di Energy Transfer è espressa in termini della sovrapposizione tra lo spettro di emissione del donatore e lo spettro di assorbimento dell’accettore. Tale contributo è incorporato riscrivendo la funzione delta di eq. 3.1 come il prodotto di due funzioni delta, che descrivono l’emissione e l’assorbimento di energia, , rispettivamente da parte del donatore e dell’accettore:
+ − − =
(3.4)
∫ − − × + −
A partire dalle eq. 3.1-3.4, la velocità di Energy Transfer può infine essere scritta in termini del coefficiente di assorbimento dell’accettore e dell’intensità di emissione normalizzata del donatore :
= ( ) ∫ ( ) ( ) (3.5)
dove e sono, rispettivamente, resa quantica di emissione e tempo di vita del donatore in assenza dell’accettore, è l’indice di rifrazione del mezzo e è il numero di Avogadro. L’eq. 3.5 può essere scritta anche in una forma semplificata come:
= (3.6)
dove il parametro è detto distanza di Förster ed è definito come:
= ( ) ∫ ( ) ( ) (3.7)
In pratica, corrisponde alla distanza D-A tale per cui la velocità di Energy Transfer eguaglia la velocità di decadimento radiativo del donatore ( = 1⁄ ); sotto tale condizione, l’efficienza dell’Energy Transfer è pari al 50%.
Il fattore geometrico è definito come:
27 o, alternativamente, come:
= (sin sin cos − 2 cos cos ) (3.9) dove: e sono gli angoli che i dipoli di transizione, rispettivamente, dell’accettore e del donatore formano con il vettore che li congiunge; è l’angolo tra i piani contenenti donatore e accettore (vedi Fig. 3.1). A seconda dell’orientazione relativa della coppia D-A, può variare da 0 a 4: per dipoli di transizione paralleli e collineari, = 4; per dipoli paralleli, = 1; per dipoli perpendicolari, = 0. Tuttavia, in molte applicazioni si assume che sia uguale a 2 3⁄ , ovvero il valore ricavabile sotto l’ipotesi che l’orientazione relativa dei dipoli di transizione del donatore e dell’accettore si randomizzi in seguito a fenomeni di diffusione rotazionale precedenti l’Energy Transfer.
A conclusione della breve presentazione della teoria di Förster qui riportata, si ricordano le condizioni sotto le quali i risultati da essa forniti possono essere considerati ragionevolmente accurati: (a) l’interazione donatore-accettore può essere appropriatamente descritta approssimando il coupling elettronico in termini di un’interazione dipolo-dipolo; (b) il tempo di vita radiativo del donatore, la forma di banda dello spettro di assorbimento dell’accettore e di quello di emissione del donatore e i dipoli di transizione non sono alterati a causa delle interazioni tra donatore e accettore; (c) i fenomeni di allargamento di riga non omogeneo sono assenti nelle bande spettrali di donatore e accettore; (d) le dinamiche secondo cui l’Energy Transfer procede sono di tipo incoerente.
3.2 Il modello di tipo IEFPCM-TDDFT
Il modello che sarà qui presentato può essere inquadrato nel filone di ricerca avente per obiettivo la formulazione di teorie che permettano una più completa ed accurata descrizione dei fenomeni di Electronic Energy Transfer, attraverso una trattazione quantomeccanica delle interazioni molecolari coinvolte in questi ultimi. In particolare, nel presente modello l’attenzione è focalizzata sugli effetti esercitati dal solvente (o, più in generale, da un mezzo dielettrico) sull’Energy Transfer stesso. Come si vedrà in dettaglio nella sezione successiva, Förster introdusse gli effetti della presenza di un mezzo dielettrico in termini di uno screening dell’interazione coulombiana tra donatore e accettore. Tale screening, tuttavia, è solo una parte degli effetti globali indotti da un ambiente polarizzabile sui processi di Energy Transfer: la presenza di un solvente infatti non solo
Fig. 3.1
Rappresentazione grafica dei parametri in termini dei quali è definito il fattore geometrico (sinistra); valori di per le diverse orientazioni relative della coppia donatore-accettore (destra).